
紐につけられたビーズといえば, 何を思い浮かべますか? マルディグラを祝う人で賑わうルイジアナ州ニューオリンズの通りや, サマーキャンプでのフレンドシップブレスレット作りなどでしょうか. あるいは, ポリマーの研究に興味がある方なら, 粘弾性流体に一定の力を加えると, 流体が紐についたビーズのように見えることを思い浮かべるかもしれません. ここでは, Oldroyd-B ポリマーを使った例を見てみましょう.
粘弾性流体
粘弾性流体とは, その名の通り, 弾性を示す流体のことです. 粘弾性流体は変形すると, ある一定の力を加えると変形前の状態に戻ろうとします. このタイプの流体の例としては, 以下のようなものがあります:
- ポリマー溶融体
- 塗料
- タンパク質の懸濁液

塗料は粘弾性流体の一種です.
2020年に COMSOL Multiphysics® ソフトウェアのバージョン5.6でリリースされた”ポリマー流れモジュール”には, 粘弾性流体モデルが含まれています. これは, 流体の弾性を考慮し, その作用力, コーティングの均一性, および金型の充填度合いを予測するために使用することができます.
“ポリマー流れモジュール”には, 以下の粘弾性流体モデルが含まれています:
- Oldroyd-B
- Gisekus
- FENE-P
- LPTT
ここでは, Oldroyd-B 流体のフィラメントが表面張力効果によって伸びる様子をモデル化した結果をご紹介します. このモデルを作成するためのステップバイステップをご覧になりたい方は, こちらからダウンロードできます: “粘弾性フィラメントのビーズオンストリング構造”.
Oldroyd-B ポリマーにおける表面張力効果のモデル化
このモデル例は, Oldroyd-B 流体の長く伸びないフィラメントから始まります. フィラメント自体は, 初期半径の摂動が小さい液柱としてモデル化され, 流れは軸対称にモデル化されます.
Oldroyd-B 流体は, ニュートン流体中のポリマーの希薄溶液としてモデル化されています. ポリマー自体は, 次の2つの物理学的パラメーターで特徴付けられます:
- 粘度
- 緩和時間
この問題は無次元であるため, 粘弾性フィラメントが細くなるときの力学をシミュレーションするために, 2つの無次元パラメーターを使用します:
- Deborah 数 (無次元ポリマー溶液の緩和時間)
- Ohnesorge 数 (慣性ー毛管と粘性ー毛管の時間スケールの比率)
結果のモデル化
以下に示すように, 異なる時間ステップでの粘弾性フィラメントの進化を決定することができます. これは, 文献の既存の実験結果やシミュレーション結果とよく一致しています(チュートリアルモデルのドキュメントの参考文献1を参照).

0, 20, 30, 100, 300秒におけるフィラメントのプロファイル (左から右へ順に).
また, モデルの結果は, フィラメントの最小半径を時間の関数として表しています. これは, フィラメントが急速にビーズオンストリング構造を形成した後, ゆっくりと糸が細くなっていくことを示しています. この糸が細くなる速度は, 表面張力と弾性力のバランスによって求められます.
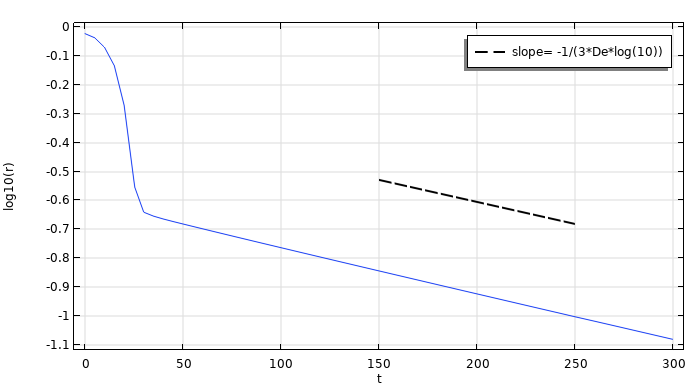
フィラメントの最小半径を時間の関数として表したもの.
緩和時間よりはるかに長い時間では, 粘弾性フィラメントは, ほぼ球状の液滴が指数関数的に細くなる糸で結ばれた状態になっています.

また, 特に粘度が低い場合や表面張力が高い場合には, ビーズオンストリング構造でサテライト液滴が形成されることもわかります. (ただし, より細かいメッシュでモデルを実行しないとこれを見ることはできません.)
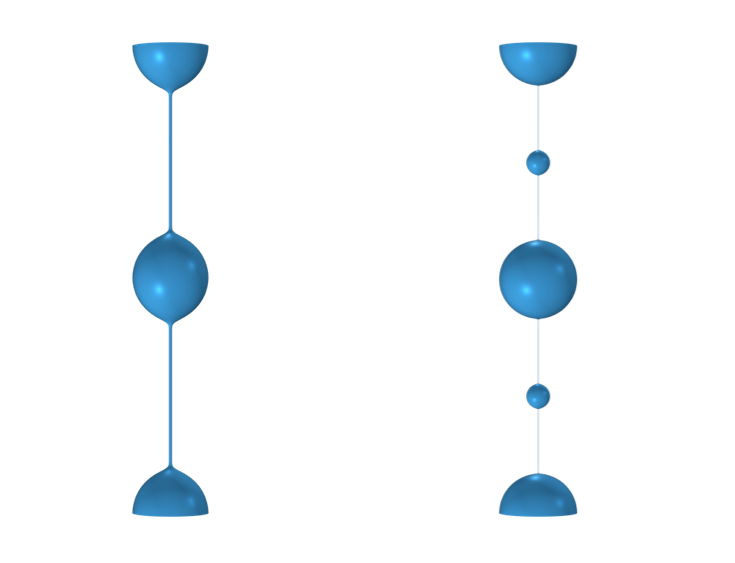
サテライト液滴がない場合 (右) とある場合 (左) の粘弾性流体のフィラメント.
ご自身で試しましょう
ここでは結果に直接飛びましたが, “粘弾性フィラメントのビーズオンストリング構造”モデルの構築方法を正確に学びたい方は, アプリケーションギャラリからドキュメントとMPHファイルをダウンロードできます.


コメント (0)