CFD モデリングに自動壁処理を使用する必要があるのはなぜですか?

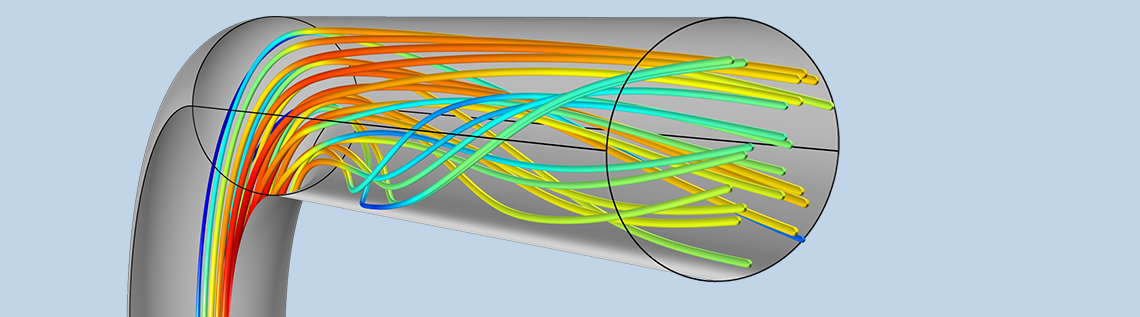
壁に囲まれた乱流は, 壁の近くで極端な勾配を示します. これらの勾配を処理する最も正確な方法は, 低レイノルズ数モデルを使用して求解することですが, これは計算コストがかかります. 産業用アプリケーションでは, 壁に最も近い流れを求解するのではなくモデル化する壁関数を使用します. 壁関数は堅牢で効率的ですが, 特に正確ではありません. COMSOL® ソフトウェアの新しい自動壁処理機能は, 壁関数と低レイノルズ数モデルの利点を組み合わせています.

自動壁処理の仕組み

COMSOL Multiphysics バージョン 5.3 の新しい自動壁処理機能は, モデルで使用可能なメッシュに定式化を適応させることにより, 壁関数の堅牢性と低レイノルズ数モデルの精度を組み合わせています. 境界層メッシュが粗い場合は, 堅牢な壁関数定式が使用されます. 境界層メッシュが密な場合は, 低レイノルズ数定式が使用され, 速度プロファイルが壁まで求解されます.

低レイノルズ数定式化と壁関数定式化の間の遷移は滑らかで, 境界要素で2つの定式化をブレンドすることで行われます. 境界要素のグリッドポイントの壁距離をリフトオフによって与えられた粘性単位で計算することにより, 2つの定式化の組み合わせが境界条件に使用されます.

下の図は, 低 Re k-ε 乱流モデルの低レイノルズ数定式化と対数壁関数の間の遷移を例示しています. 粘性単位での壁距離 y+ は, 乱流散逸率 ε に対してプロットされています. 緑の曲線は ε の低 Re 定式化, 青の曲線は壁関数表現, 赤の曲線は自動壁処理に使用される Wolfshtein モデルです. y+ 値が 1 ～ 20 の範囲, つまりバッファー層で Wolfshtein モデル (赤) で得られた滑らかな遷移を確認してください.

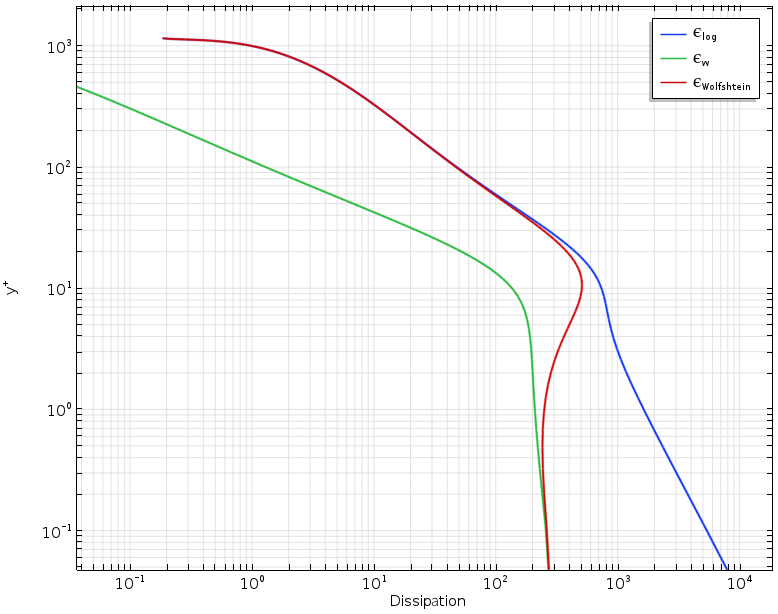
低 Re 定式 (緑), 壁関数 (青), 自動壁処理 (赤).

モデルの定義を確認するには, 下の図に示すように, 境界に y+ 変数をプロットして, 壁の処理方法を調べることができます. このパイプエルボーベンチマークモデルでは, 曲げ部の内側の曲面では低レイノルズ数定式が優勢であるのに対し, パイプの直線部では壁関数定式が優勢であることがわかります.

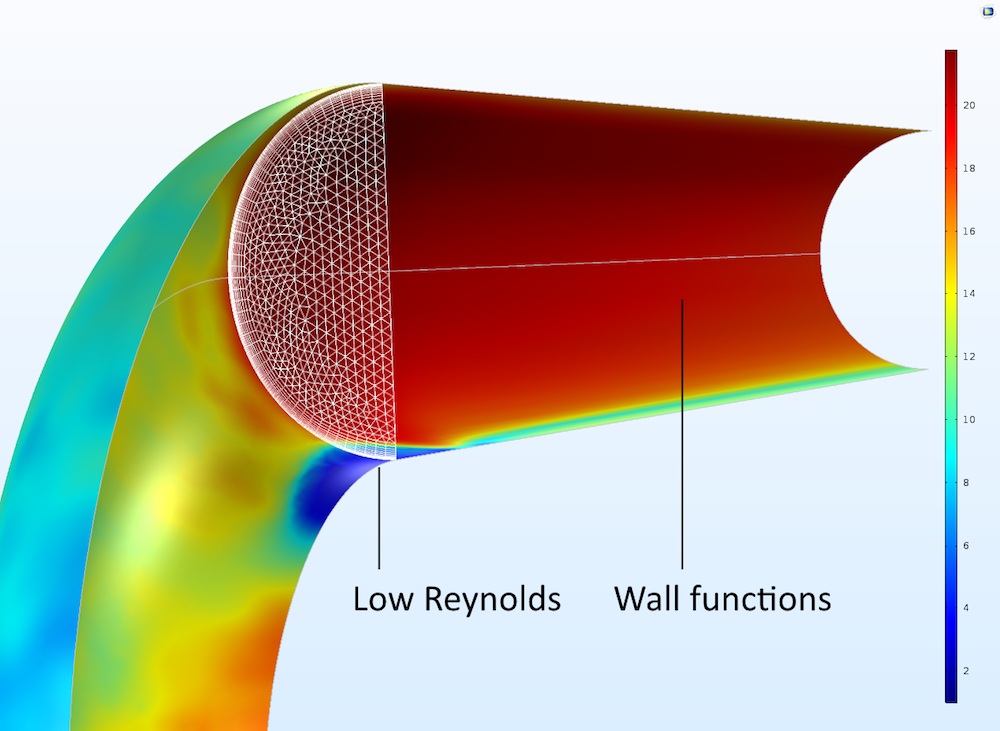
濃い赤の領域は y+ または約 20 の値を持ち, 青の領域は約 1 です.

自動壁処理による幅広い問題への対応

自動壁処理機能により, 低レイノルズ数モデルをより幅広い問題に使用できます. 例としては, 特定の表面が熱流束, 化学反応, または流体構造相互作用にさらされる結合問題があります. すべてのサーフェスに高密度メッシュを使用する (計算コストが非常に高くなる可能性がある) 代わりに, 境界層を正確に求解する必要がある関連サーフェスにのみ高密度メッシュを適用できます.

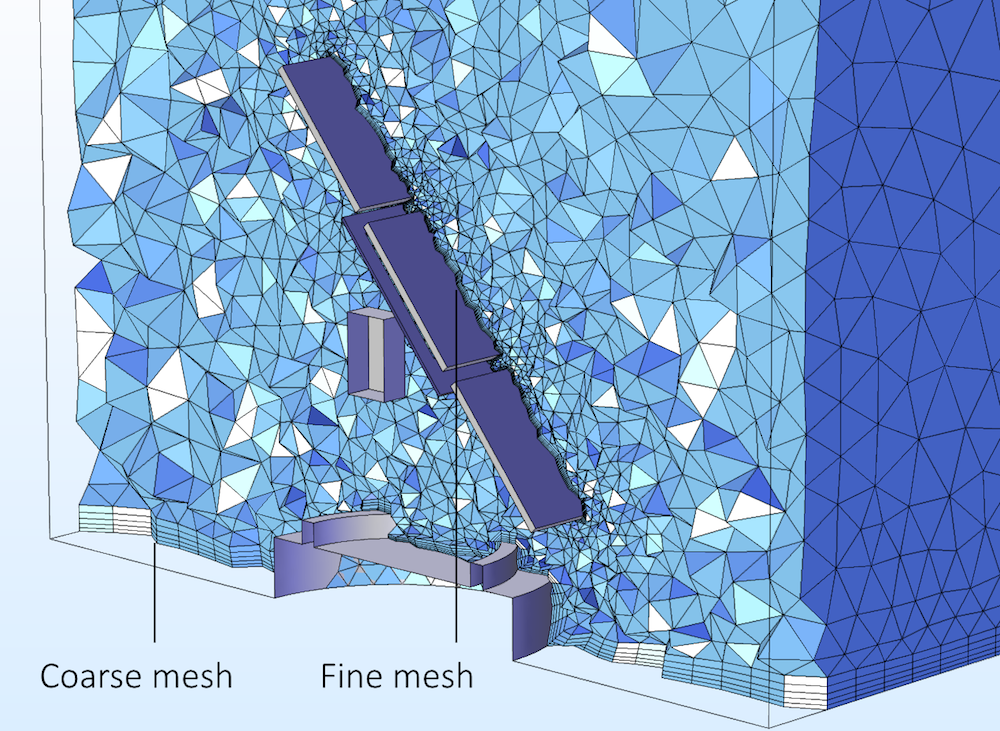
下の図は, アプリケーションライブラリのソーラーパネルモデルの境界層メッシュを示しています. パネルの表面のメッシュは, タイトな境界要素で高密度であることがわかります. これらのサーフェスでは, 応力とひずみ, および変位を計算するために, 流体が構造に及ぼす力を高精度で計算する必要があります. コンクリートベースは風の力の影響を受けないため, これらのサーフェス上の力には同じ精度は必要ありません. 自動壁処理機能を使用すると, 計算 ボタンをクリックするだけでこの問題を求解できますが, 従来の低レイノルズ数モデルでは, 収束するためにすべての境界に高密度境界層メッシュが必要になります.

このソーラーパネルの流体構造相互作用チュートリアルでは, 地面とコンクリート基礎には粗い境界層メッシュを使用し, 力を正確に計算する必要があるパネルの表面には細かいメッシュを使用できます.

簡素化されたモデル開発

新しい機能は, モデル開発にも大いに役立ちます. 適切な仮定と境界条件を求解するには, 最初のステップとして粗いメッシュで迅速な結果が必要になる場合があります. モデルの定式化を確認したら, メッシュを改良してより正確な結果を得ることができます. 自動壁処理機能により, 最小限の障害と操作でこのタイプのモデル開発が可能になります. 必要なのは “メッシュを改良する” ことだけです.

この新しい機能が提供する堅牢性により, 低レイノルズ数の乱流モデルの使用も一般的に簡素化されます. 一般的な手順は, 高レイノルズ数モデルで壁関数を使用してモデル方程式を解き, この解を低レイノルズ数モデルの開始推測として使用することです. 適応型壁処理により, この手順は粗いメッシュと細かいメッシュのモデル方程式の連続的な解法にまで簡略化されます. つまり, 最初のステップとして高レイノルズ数モデルの定式化と解法を行う必要がなくなります.

乱流インターフェース

CFD モジュールの最新バージョンでは, すべての低レイノルズ数乱流モデルインターフェースで自動壁処理が利用できます:

• k-ω
• 低レイノルズ k-ε
• SST
• v2-f
• Spalart-Allmaras
• L-VEL
• 代数 y+

自動壁処理機能は, 上記のすべての流れインターフェースの設定ウィンドウで利用できます. 下の図は, 乱流, k-ω インターフェースの選択を示しています. この流れインターフェースでは, 自動, 壁関数, 低レイノルズ数の3つの異なる壁処理オプションから選択できます.

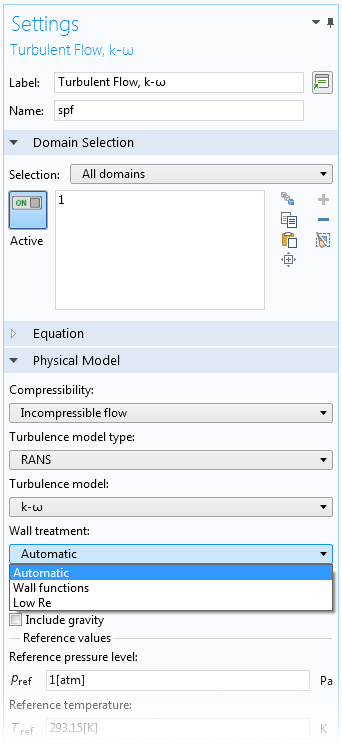
乱流, k-ω インターフェースで利用可能な3つのオプション: 自動, 壁関数, 低レイノルズ数.

その他のリソース

• 自動壁処理機能が実際にどのように機能するかを確認するには, 次のサンプルモデルを自分で試してください:
  • パイプエルボーを通る流れ
  • Ahmed ボディ上の気流