Menu
COMSOL ブログ

COMSOL® にて最尤法によるパラメーター推定を使用する方法

Author Image

Kristian Ejlebjærg Jensen 著

2022年 5月 13日

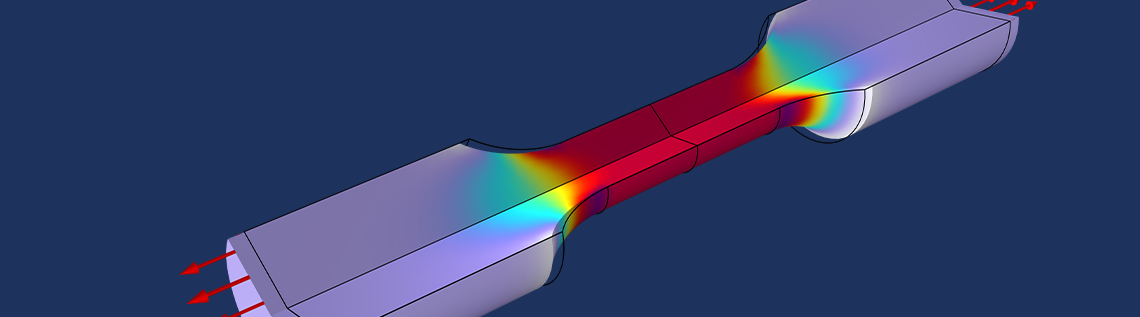
パラメーター推定は, 目を引くような図解はほとんどありませんが, 正確な材料データ, ひいては正確なシミュレーション結果を得るために重要な役割を果たします. パラメーター推定では, 測定された実験結果とモデル内の対応するデータとの差を最小にすることが求められます. 時には, 複数の実験から得られたデータを組み合わせる必要がありますが, その場合, すべての実験が推定される材料パラメーターに情報を提供するように, 適切な重みを設定しなければなりません. 最尤法によるパラメーター推定では, 客観的な基準に基づいて重みを自動的に選択し, 実験から最大限の情報が抽出できます.

最小二乗法による手動調整の回避

最小二乗法は, 最尤法によるパラメーター推定の特殊なケースで, 基本的なパラメーター推定の出発点として, よく利用されている一般的な手法です. COMSOL Multiphysics® ソフトウェアには, 最小二乗法をサポートする機能が搭載されています.

このブログでは, 最尤法によるパラメーター推定を利用することで, 与えられた問題に対して手動で重みを調整する必要性を回避する方法をご紹介します.

ヤング率の相対誤差が減少していることを青線, ポアソン比の相対誤差が増加していることを緑線で表したグラフ.
この例では, 2つのパラメーターの相対誤差は, 2組の測定値に対して選択された重みに依存します. したがって, 両方のパラメーターを正確に決定するには, 2つの重みの間で適切な妥協点を見つけることが必要になります.

データサンプリングにおける確率と統計

確率密度関数 f に対して, ある範囲 [a, b] にあるデータポイントをサンプリングする確率 P は次の積分値で与えられます.

P=\int_a^bf(x)dx

このとき, 測定値 x の周りの無限小の範囲 dx しか考慮しないため, 確率は次のようになります.

P=f(x)dx

この意味では, 確率密度関数と dx によって与えられる確率の間には直接的な関係があります. (dx は表記上の都合で省略可)

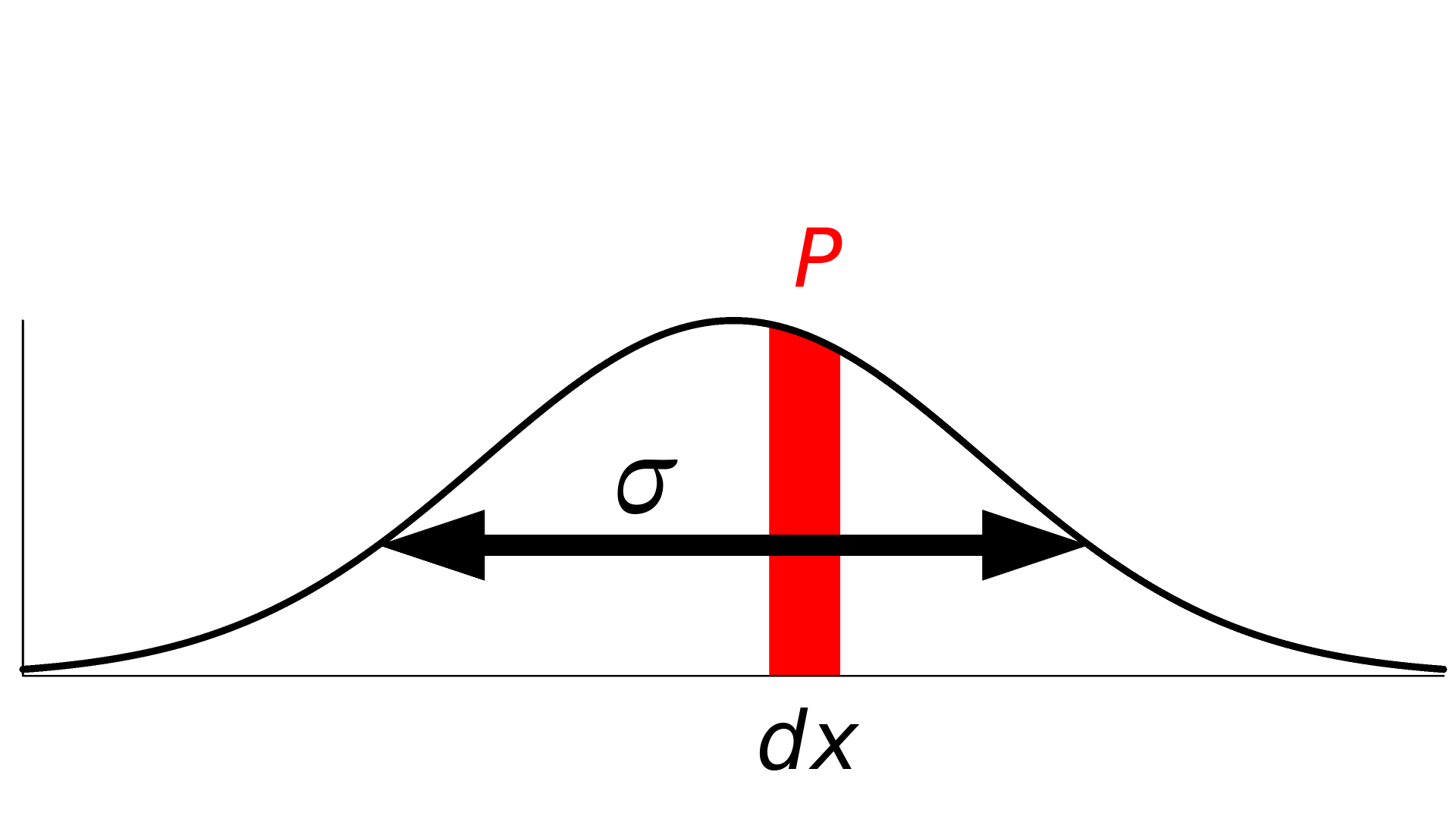
測定誤差の標準偏差, 無限小の範囲, 確率をラベル付けしたベルカーブ. 確率は赤でハイライトされています.
特定の値をサンプリングする確率は, 確率密度関数を積分することで計算することができます.

最小二乗目的関数と最尤法によるパラメーター推定

シミュレーションと実験との間の不一致の原因として, 様々なものが考えられます. 以下の例では, 実測値から正規分布の不確実性を考慮するため, ある値 x^e を測定する確率は次のようになります.

g(x-x^e,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-x^e)^2}{2\sigma^2}}

ここで, \sigma は測定誤差の標準偏差で, x は平均値です. n個 の測定値に対して, 結合尤度を積として計算できます.

P=\prod_i^n g(x_i,x_i^e,\sigma) = \prod_i^n \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x_i-x_i^e)^2}{2\sigma^2}}

尤度の対数をとることで, 積やそれに伴う数値的な困難さを回避することができます. 代わりに, 最小二乗目的関数に類似している合計が得られます:

\log(P) &=& \sum_i^n \log\left(\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x_i-x_i^e)^2}{2\sigma^2}}\right) \\
&=& \sum_i^n\left( -\frac{(x_i-x_i^e)^2}{2\sigma^2}-\log\left(\sigma\sqrt{2\pi}\right)\right)\Leftrightarrow \\
-\log(P) &=& n\log\left(\sigma\sqrt{2\pi}\right) + \frac{_1}{^2}\sum_i^n\frac{(x_i-x_i^e)^2}{\sigma^2}

いわば, \sigma は最小二乗目的関数における重みのような役割を担っていると言えます. したがって, 尤度を最大にするには, 式の右辺を最小にする必要があり, \sigma に関係なく, 偏差の二乗の和が最小値をとるときに最小となります. もし, \sigma の異なる測定値があれば, 同じ結論は得られません. そのような例を調べてみましょう.

引張試験のための最尤法

材料のポアソン比は圧縮試験で推定するのが一般的ですが, ここではデモンストレーションとして, 引張試験でヤング率とともにポアソン比を推定する例を考えてみます. これを行うには, 下図に示す試験片の引張力と半径方向の収縮を測定します.

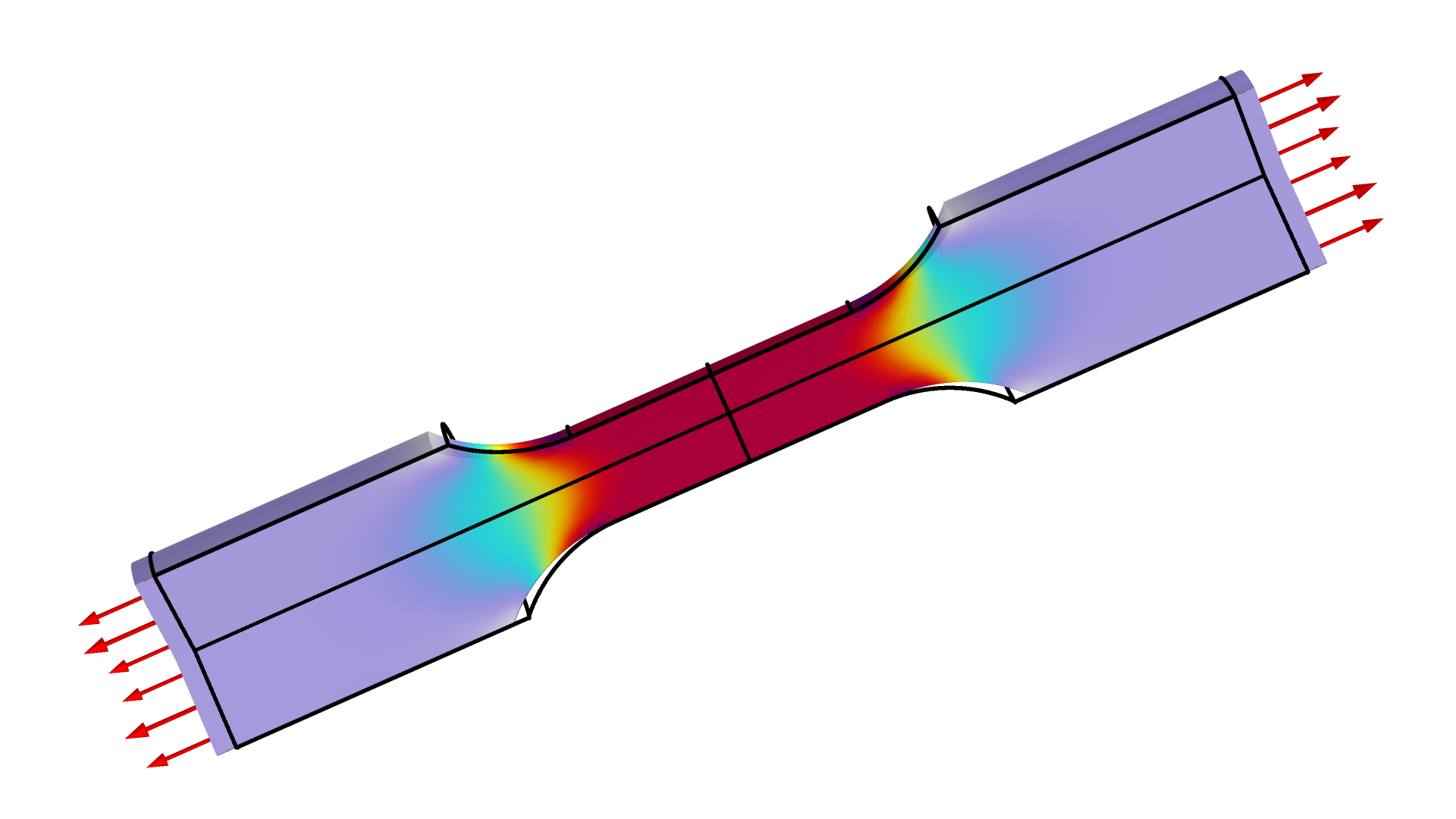
引張試験の応力を示すモデル. 両端が紫色で外側に矢印があり, 中央が赤色になっています.
図は, 引張試験の応力を示しています. 力と中心半径方向変位は伸張の関数として測定されます.

力と変位の測定データには10桁程度の差があるため (SI単位の場合), 通常の最小二乗法では, 両方の材料パラメーターについて正確な結果を得るためには, 最小二乗目的関数の重みを調整する必要があります. しかし, 2つの測定誤差の標準偏差 \sigma_F と \sigma_r をコントロールとして用いることで, 自動的に最尤法で最適な重みを計算することができます. すなわち, 次のようになります.

P_F &=& \prod_i^ng(F_i-F_i^e,\sigma_F) \quad \mathrm{and} \quad P_r = \prod_i^n g(r_i-r_i^e,\sigma_r) \\
P &=& P_F P_r \Leftrightarrow -\log(P)=-\log(P_f)-\log(P_r)

COMSOL Multiphysics には最小二乗目的関数が組み込まれているため, 最尤法によるパラメーター推定の問題を求解するためのカスタム目的関数を簡単に定義することができます. アプリケーションギャラリにある “最尤法によるパラメーター推定” モデル は, 正規分布のノイズを加えて合成データを生成します. そして, モデルはこのデータをもとに材料パラメーターと標準偏差を復元します. その結果, 下図のような応力と半径方向の変位が得られます.

回復された半径の変化と応力
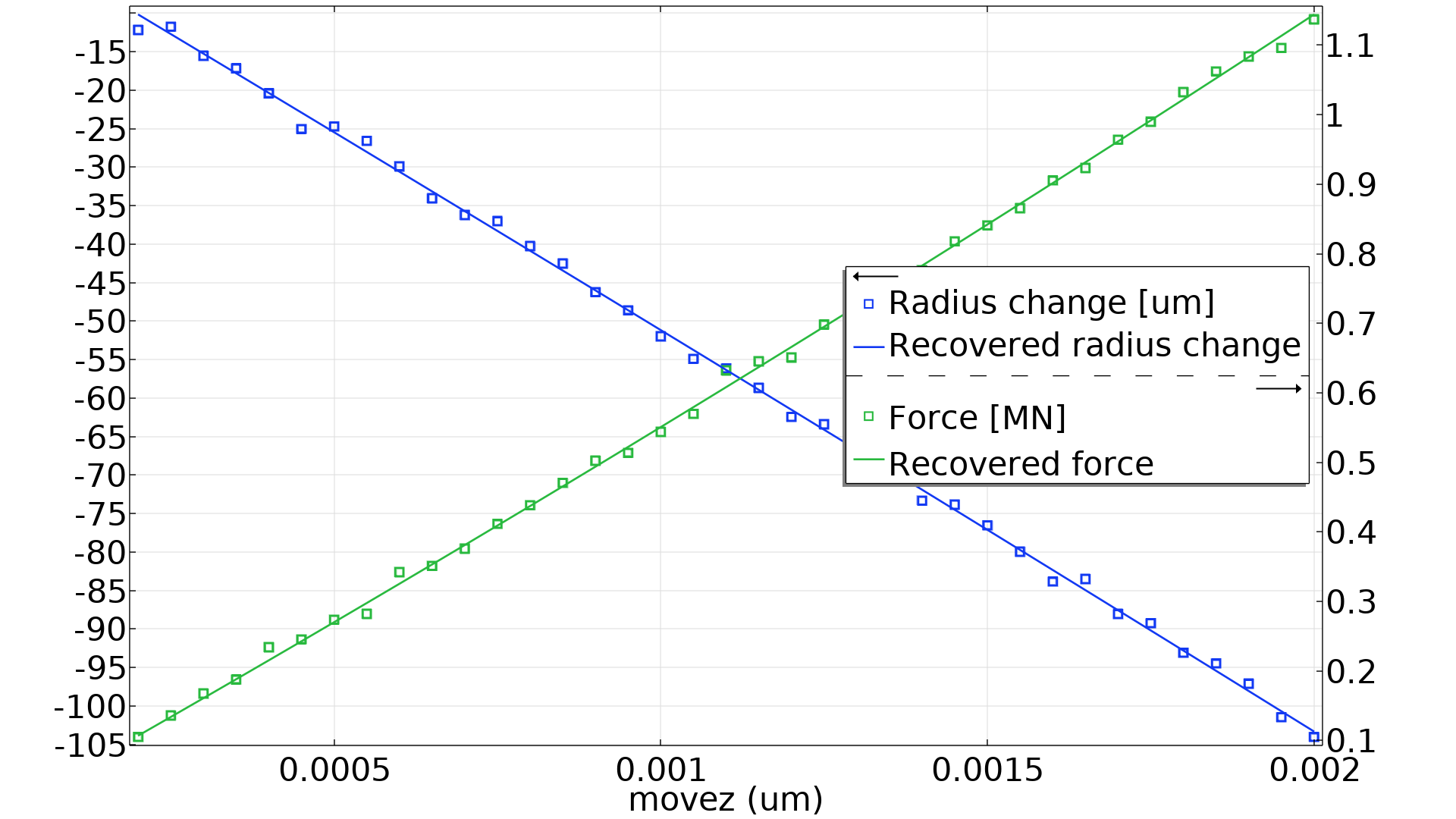
ノイズの多いデータと最適化されたモデルの挙動を伸縮の関数としてプロットしたものです. 2つの測定にはそれぞれ37のデータポイントがあります.

このモデルでは, 材料パラメーターを 0.1–0.5%, 標準偏差を 6% 程度の精度で復元することができますが, 測定回数が増えるにつれて精度が向上することが予想されます.

今回のブログでは, 標準偏差が固定された正規分布ノイズの場合に焦点を当てましたが, 最尤法によるパラメーター推定という方法は, 特定の実験に合わせて拡張することができ, 最適かつ一貫した方法で情報が抽出できるようになっています.

試してみましょう

“最尤法によるパラメーター推定” モデルをご自身でお試しいただきたい方は, 以下のボタンをクリックしてアプリケーションギャラリのエントリにアクセスしてください.

チュートリアルモデルを取得

参考文献

パラメーター推定の例をもっと詳しく知りたい方は, ぜひこちらのモデルをご覧ください.

パラメーター推定について詳しく知りたい方は, 以下の資料をご覧ください.

コメント (0)

コメントを残す
ログイン | 登録
Loading...
COMSOL ブログを探索
カテゴリー
タグ