COMSOL ブログ

吸音境界: 局所反応と拡張反応

Takumi Yoshida 著

2025年 1月 10日

今日, 室内音響シミュレーションは, 没入感のある仮想シーンの作成, 室内の快適な音響環境の設計, オーディオ体験の最適化など, 優れたサウンドを設計する上で不可欠な要素となっています. COMSOL Multiphysics^® ソフトウェアのアドオンである 音響モジュール には, 室内音響シミュレーションに適した複数のインターフェースが含まれています. このブログでは, 室内音響モデリングにおける吸音境界条件の重要性に焦点を当てます.

吸音性能

吸音境界条件を理解するために, まず吸音係数について説明します. 吸音材の吸収特性を表すために, 次の3つの量が使用されます (文献1):

吸音係数, \alpha: 反射されない音エネルギーと入射する音エネルギーの比
比音響インピーダンス, Z_{\rm n}: 音圧と吸音材表面の法線粒子速度の比
複素圧力反射係数, R: 反射される音圧と入射圧力の比

次に, 平面波が多孔質吸音材に入る理想的な状況でこれらのパラメーターを分析します. この状況については, 以下で説明します.

多孔質材料に入射する平面波.

ここで, 空気と多孔質材料の波数はそれぞれ k と k_{\rm e} であると仮定します. 入射, 反射, 透過音圧はそれぞれ p_{\rm i}, p_{\rm r}, p_{\rm t} です. 入射, 反射, 透過角度はそれぞれ \theta, \psi, \phi です. 入射音と反射音の振幅は A_{\rm i} と A_{\rm r} で表され, 最後に B_{\rm t} と B_{\rm b} は多孔質媒体内の進行音と逆行音を表します. 厚さ d m の多孔質吸収体が等価流体であると想定されました (詳細については, Multiphysics Cyclopedia を参照してください). 剛体境界による終端は x=d に設定されました.

線形音波方程式から, 入射音, 反射音, 透過音の x 方向の粒子速度 (それぞれ v_{\rm i}, v_{\rm r}, v_{\rm t}) は次のように表すことができます:

v_{\rm i}(x)=\frac{\cos{\theta}}{Z_0}p_{\rm i}(x)

v_{\rm r}(x)=-\frac{\cos{\psi}}{Z_0}p_{\rm r}(x)

v_{\rm t}(x)=\frac{B_{\rm t}\cos{\phi}}{Z_{\rm C}}\exp{(-jk_{\rm e}x\cos{\phi})}-\frac{B_{\rm b}\cos{\phi}}{Z_{\rm C}}\exp{(jk_{\rm e}x\cos{\phi})}

ここで, Z_{\rm 0} と Z_{\rm C} は, 空気と多孔質材料の特性インピーダンスを表します. 定義から, 反射係数は次のように表されます:

R=\frac{p_{\rm r}(0)}{p_{\rm i}(0)}

空気と多孔質層 (x=0) の境界面には, 次の2つの連続条件が課されます:

p_{\rm i}(0)+p_{\rm r}(0)=p_{\rm t}(0)

v_{\rm i}(0)-v_{\rm r}(0)=v_{\rm t}(0)

これらの連続条件とフェルマーの原理 \theta=\phi を用いると, 特定の音響インピーダンスは次のように表すことができます:

Z_{\rm n}=\frac{p_{\rm t}(0)}{v_{\rm t}(0)}=\frac{p_{\rm i}(0)+p_{\rm r}(0)}{v_{\rm i}(0)-v_{\rm r}(0)}=\frac{Z_0}{\cos{\theta}}\frac{1+R}{1-R}

したがって,

R=\frac{Z_{\rm n}\cos\theta-Z_0}{Z_{\rm n}\cos\theta+Z_0}

吸収係数は次の式で決定できます.

\alpha = 1-|R|^2 = 1 – |\frac{Z_{\rm n}\cos\theta-Z_0}{Z_{\rm n}\cos\theta+Z_0}|^2

したがって, 境界に3つの量のいずれかを割り当てることで, 境界での吸音をモデル化できます. また, 上記の式は, \alpha が本質的に入射角に依存することを示しています. R と Z_{\rm n} は位相情報を含む複雑なパラメーターですが,\alpha はエネルギーパラメーターです. 位相情報は, 部屋のモードを正確にシミュレートするために重要です. したがって, 一般に, 波ベースの室内音響シミュレーションでは, 複雑なパラメーターの方が入力として適しています. 一方, 吸音係数は, 吸音材の性能を直感的に読み取るのに適しており, 吸音テストの主な出力です. ランダム入射吸収係数は, 立体角にわたる平均値であり, 吸収体の実際の性能として採用されます.

次の式では, 多孔質材料の音響インピーダンスをさらに調べます.

x=0 での透過圧力と速度は次のとおりです:

p_{\rm t}(0)=B_{\rm t} + B_{\rm b}

v_{\rm t}(0)=\frac{(B_{\rm t} – B_{\rm b})\cos\phi}{Z_{\rm C}}

一方, those at x=d の場合は次のとおりです:

p_{\rm t}(d)=(B_{\rm t} + B_{\rm b})\cos{(k_{\rm e}d\cos\phi)} – (B_{\rm t} – B_{\rm b})\sin{(k_{\rm e}d\cos\phi)}

v_{\rm t}(d)=\frac{(B_{\rm t} – B_{\rm b})\cos\phi}{Z_{\rm C}}\cos{(k_{\rm e}d\cos\phi)} – j\frac{(B_{\rm t} + B_{\rm b})\cos\phi}{Z_{\rm C}}\sin{(k_{\rm e}d\cos\phi)}

これらの式を使用して, 入口のパラメーターを終端値とともに次の行列形式で表すことができます:

\begin{bmatrix}
p_{\rm t}(0) \\
v_{\rm t}(0) \\
\end{bmatrix}=\begin{bmatrix}
\cos{(k_{\rm e}d\cos\phi)} & j\frac{Z_{\rm C}}{\cos\phi}sin{(k_{\rm e}d\cos\phi)} \\
j\frac{\cos\phi}{Z_{\rm C}}sin{(k_{\rm e}d\cos\phi)} & \cos{(k_{\rm e}d\cos\phi) \\
\end{bmatrix}
\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}={\bm T}_{\rm F}\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}

ここで, {\bm T}_{\rm F} は流体層の伝達行列であり, 伝達行列法 (TMM) を用いた吸音と遮音のモデル化に広く使用されている (文献2). スネルの法則 ksin\theta = k_{\rm e}\sin\phi を用いると,

{\bm T}_{\rm F}=\begin{bmatrix}
\cos{(k_{\rm n}d)} & jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}sin{(k_{\rm n}d)} \\
j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)} & \cos{(k_{\rm n}d) \\
\end{bmatrix}

ここで, k_{\rm n}=(k_{\rm e}^2-k^2\sin^2{\theta})^{\frac{1}{2}} です. 端末上の固定境界条件 (v_{\rm t}(d) = 0) の下では, 多孔質吸収体の比音響インピーダンスは次のように計算できます:

Z_{\rm n}=\frac{p_{\rm t}(0)}{v_{\rm t}(0)} = \frac{\cos{k_{\rm n}d}}{j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)}}=-jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}\cot{(k_{\rm n}d)}

上記の式は, 比音響インピーダンス自体が角度に依存することを示しています. したがって, 境界での音響吸収を完全にモデル化するには, 吸収体インピーダンスの角度依存性を考慮する必要があります.

ローカルおよび拡張反応モデル

境界での吸音をモデル化する場合, ローカルおよび拡張反応モデルの2種類の吸音境界モデルが採用されます. 室内音響シミュレーションの標準であるローカル反応モデルは, 角度に依存しないインピーダンス (通常は通常の入射条件のインピーダンス値を使用) を使用して境界の吸音特性を記述します. 吸音材の表面上の特定のポイントでの粒子速度は, 表面上の他のポイントでの挙動とは無関係であると想定されます. 拡張反応モデルは, 角度に依存するインピーダンスを適応させます. もちろん, ローカル反応モデルは近似的ですが, 効率的であり, 高い流動抵抗を持つ剛性のある多孔質材料やハニカムコアを備えた吸音材など, 音響インピーダンスが角度にほとんど依存しない吸音材をモデル化するのに適しています. 拡張反応モデルは正確ですが, 通常は吸音材内部の追加モデル化が必要です. 正確で効率的な室内音響モデル化を実現するには, 部屋に設置された吸音材に適した吸音境界モデルを選択する必要があります. 以下では, 吸収境界タイプがランダム入射吸収係数に与える影響を理論的および数値的に実証しています.

さまざまな表面モデルが吸収性能に与える影響

剛性のある裏打ちの多孔質吸収体と, その背後に空気層がある音響カーテンの吸収性能を評価しました. 多孔質材料は, 厚さ 100 mm の等価流体と見なされました. 流体特性は, 流動抵抗が 13,900 Pa s/m² の経験的 Miki モデルを使用してモデル化されました. 使用した音響カーテンは, 調査対象の周波数の波長に対して非常に薄いため, 透過膜モデルが使用され, 空気層と結合されました. 透過膜モデルでは, カーテンの伝達インピーダンスは次の式で計算されました:

Z_{\rm t}=(\frac{1}{R_{\rm C}}+\frac{1}{j\omega M_{\rm C}})^{-1}

ここで, R_{\rm C} と M_{\rm C} は流れ抵抗と表面密度を表し, それぞれ 416 Pa s/m と 0.5 kg/m² に設定されました. 理論的研究には TMM が使用され, 統計的吸収係数はランダム入射値として評価されました. 統計的吸収係数 \alpha_{\rm s} の定義を以下に示します:

\alpha_{\rm s}=\frac{\int_0^{\pi/2}\alpha(\theta)\sin\theta\cos\theta d\theta}{\int_0^{\pi/2}\sin\theta\cos\theta d\theta}

薄い材料の伝達行列 {\bm T}_{\rm T} は次のように表されます:

{\bm T}_{\rm T}=\begin{bmatrix}
1 & Z_{\rm t} \\
0 & 1 \\
\end{bmatrix}

上記の伝達行列を使用すると, 空気層のある音響カーテンの比音響インピーダンスは次のようになります:

Z_{\rm n} = Z_{\rm t}-jZ_{\rm 0}\cot{(kd\cos\theta)}

TMM の場合, ローカル反応モデルは \theta=0 を代入することで評価できます.

数値調査では, 残響室で測定された吸収係数である残響室吸収係数を計算します. 係数の値は, 測定された部屋とサンプルサイズによって異なります. 吸収係数は, ISO:354 で早くも測定手順として標準化されており, 実際の部屋の音響設計で広く使用されています.

COMSOL Multiphysics^® を使用して残響室吸収係数の測定を効率的にシミュレートするために, 以下に示すように, 埋め込まれた吸音材を備えた唯一のハードフロアを2次元でモデル化しました.

残響室の吸収係数を評価するための埋め込み吸音材モデル.

文献3の検証研究では, この簡略化されたモデルが残響係数の測定値に非常に近似していることが示されました.

圧力音響 (境界要素) インターフェースは入射圧力場と剛床のモデル化に使用され, 圧力音響 (周波数領域) インターフェースは吸収体内部の圧力のモデル化に, 多孔質音響 機能は多孔質材料に使用されています. 音響 FEM–BEM 境界 機能を使用すると, 音響カーテンの伝達インピーダンスを同時に設定できます. 局所反応モデリングの場合, 吸収体領域は無効になり, 対応する法線入射音響インピーダンスが吸収体の表面に割り当てられます. 残響室の吸収係数の評価は, 次の手順で行います:

入射角 \theta_n の平面波に対する吸収体表面の入射 W_{{\rm i},\theta_n} と吸収エネルギー W_{{\rm a},\theta_n} を評価します.
次の式を使用して, 吸収エネルギーの合計と入射エネルギーの合計の比を計算します.

残響室の吸収係数 \alpha_{\rm r} を以下に示します.

\alpha_{\rm r}=\frac{\sum_{n=1}^{N}W_{{\rm a},\theta_n}}{\sum_{n=1}^{N}W_{{\rm i},\theta_n}}

ここで, N は入射角の数です. 数値テストでは, 平面波入射場は 背景圧力場 でモデル化され, W_{{\rm i},\theta_n} と W_{{\rm a},\theta_n} は次のように定義されました:

W_{{\rm i},\theta_n}=\int \frac{p_0^2}{2Z_{\rm 0}}\cos\theta_n dS

W_{{\rm a},\theta_n}=\int {\bm n}\cdot {\bm I}_{\theta_n}dS

ここで, p_0 は入射圧力の振幅, \bm n と {\bm I}_{\theta_n} は吸音材表面の入射角 {\theta_n} の法線ベクトルと音の強度ベクトルです.

以下のグラフは, 多孔質吸収体のランダム入射吸収係数を比較したものです. 局所反応と拡張反応の差は小さいですが, 特に高周波数ではその差が見られます. したがって, 上で例示したように, 局所反応モデルは, 高い流動抵抗と剛性端を持つ多孔質材料の近似として適しているようです.

多孔質吸収体のランダム入射吸収係数.

一方, 以下に示す音響カーテンのランダム入射吸収係数の比較では, 局所反応モデルと拡張反応モデルの間に大きな相違が見られます. これは, 空気層の強い入射角依存性によるものです. また, 空気層のある吸収体では拡張反応モデリングが重要であるという従来のルールにも対応しています.

音響カーテンのランダム入射吸収係数.

残響室の吸収係数と統計値の比較?

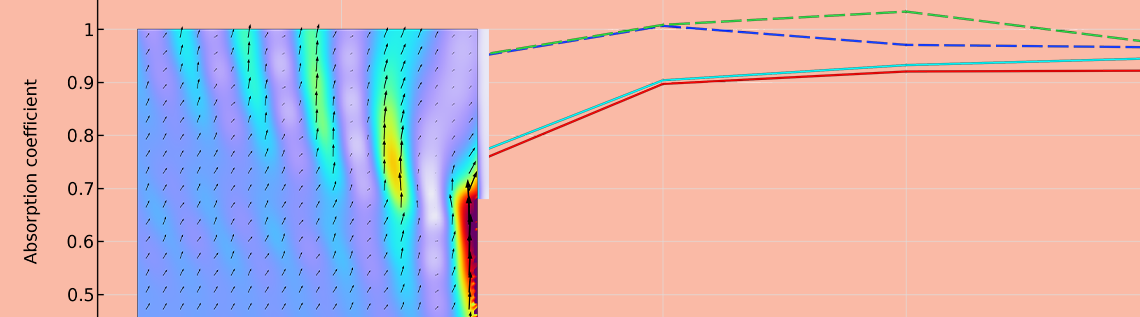
上記の吸収係数グラフに示されているように, 吸収体と吸収境界モデルの種類に関係なく, 残響室の吸収係数は統計値よりも大きく, 1 (完全吸収を超える) を超えています. この現象は エッジ効果 と呼ばれ, 実際の測定では一般的であり, 剛性床から吸収体表面へのエネルギーの流れによって発生します. このような状況は, 500 Hz で入射角 60^° の場合の音響カーテンの拡張モデルに対して示されています. エネルギー流れは, サンプルエッジ周辺の音圧勾配によって発生します. 床面近くの音圧は反射音の寄与により大きな値をとりますが, 吸音材前面の音圧は吸音効果により小さくなります. エネルギー流れはサンプルエッジ周辺で発生し, サンプル面積を増やすことで吸音率への影響を減らすことができます. そのため, 残響室吸音率を測定するためのサンプルサイズは, ISO:354 で規定されています.

入射角 60^° における 500 Hz での音響強度の振幅と矢印の可視化.

結論

このブログでは, 境界での吸音の理論的側面を紹介し, 吸音境界モデルの種類が吸音性能にどのように影響するかを検討しました. 室内音響モデリングには, COMSOL^® のフィジックスインターフェースとして, 音線音響, 圧力音響 (周波数領域) および 圧力音響 (陽的時間発展) インターフェースが適しています. 音線音響 インターフェースは幾何音響に基づいており, 音響波の挙動を正確に捉えることはできません. ただし, この実装では, 表面での吸音の入射角依存性の挙動を捉えることができるため, 室内音響モデリングの精度が向上します.

波動ベースのアプローチでは, 境界での吸音特性を正確にモデル化します. 多孔質音響 機能と 内部インピーダンス 機能は, 吸音境界の拡張された反応性をモデル化するために使用されます. 圧力音響 (周波数領域) インターフェースは, 本質的に周波数に依存する方法であるため, これらの条件を簡単に処理できます. 一方, 拡張反応境界条件の時間領域モデリングは, 吸収特性の周波数依存性を時間領域でモデリングするのが難しいため, 非常に困難です. ただし, 時間領域で 多孔質音響 機能を使用して, 拡張反応性を備えた多孔質吸収体をモデリングできます. この機能の時間領域バージョンでは, 効率的な補助微分方程式法を使用して, 多孔質材料の周波数依存性を考慮します. したがって, 吸収体の構成に応じて, 吸音境界モデルを柔軟に選択できます.

今後のブログでは, 時間領域の 多孔質音響 機能を使用して, 吸音境界タイプの選択が会議室の音響にどのように影響するかを解析し, 説明します.

参考文献

Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.

コメント (0)

COMSOL ブログを探索

吸音境界: 局所反応と拡張反応