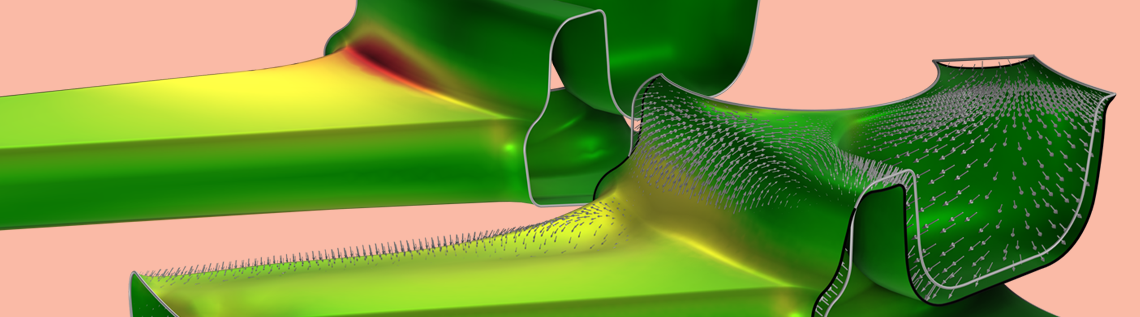
多くの疲労評価指標は応力評価に基づいていますが, 勾配ベースの最適化などの高性能な最適化手法とは相容れません. このため, 最適化手法を直接適用して疲労性能を改善することは困難です. このブログでは, 疲労挙動を改善するための試行錯誤的アプローチとして応力最小化を使用する方法を示します. この方法は, 勾配ベースの最適化に依存し, 設計の質量および剛性特性を維持しながら, 何千もの設計変数を改善します.
疲労の理解
部品が繰り返し荷重を受けると, 材料に小さな亀裂が生じることがあり ます. この発生, 進展, 最終的な破壊の進行が疲労破壊プロセスを定義します. ほとんどの実用的な状況では, き裂が発生した後の進展段階を制御することは困難な作業であるため, き裂の発生を完全に防止することが目標となります. 疲労解析の目的は, き裂が発生するまでに部品が耐えられる荷重サイクル数を計算する ことです. これにより, 疲労寿命が定義されます.

de Havilland Cometは, 窓の近くに開けられたリベットの穴から疲労亀裂が入り, 飛行中にばらばらになった飛行機です. このようなことが再び起こらないようにするために, 後のバージョンの飛行機では接着剤で取り付けられた窓が使用されました. Completeaerogeek による画像. CC BY-SA 4.0 に基づいてライセンスが付与されています Wikimedia Commons.
疲労き裂の発生は, 部品にかかる荷重とその荷重が発生させる応力に依存します. 疲労き裂は, 材料の降伏応力をはるかに下回る応力レベルで発生する可能性があり, 荷重の反復性が疲労き裂発生の主な要因であることに注意する必要があります. しかし, 設計の観点からは, 負荷の繰返し挙動を無視し, 代わりに静的な負荷ケースを考慮して高応力領域を特定することが有用な場合があります.
応力最小化
最大応力の最小化は構造力学において一般的な目的ですが, 最大応力の正確な位置が最適化の過程で変化する可能性があるため, このような最適化問題は実際には解くのが困難です. そのため, 最大応力を近似する応力集約法を使用するのが一般的で, 特にフォン・ミーゼス応力のpノルムを使用するのがよく知られています:
近似の精度はp\rightarrow\inftyのように向上しますが, これは勾配がより急激に変化し, 数値的な問題につながります. 従って, トポロジ最適化に10より大きな値が使われることはほとんどありません.
ただし, このブログでは形状の最適化に焦点を当てており, 数値的な問題を引き起こすことなく最大 50 までの大きな値を使用できる場合があります. COMSOL アプリケーションギャラリ ( たとえば, フライホイールプロファイルの最適化や最大応力制約を伴う荷重膝構造のトポロジ最適化モデルなどです. ). 次の例では, この目的関数が疲労挙動に関する形状最適化への試行錯誤的なアプローチとして使用できることを示します.
ブラケットの結果
最初の例はブラケットのジオメトリで, 構造力学のさまざまな概念を示すために使用されます. (詳細については, ブラケット – 疲労評価による応力最適化 モデルを確認してください. ) 下の図では, 荷重と境界条件が応力分布とともに示されています. 人為的な応力集中を避けるため, 固定穴にはスプリングが使用されています. あるいは, モデルを拡張してボルトを含めることもできます.
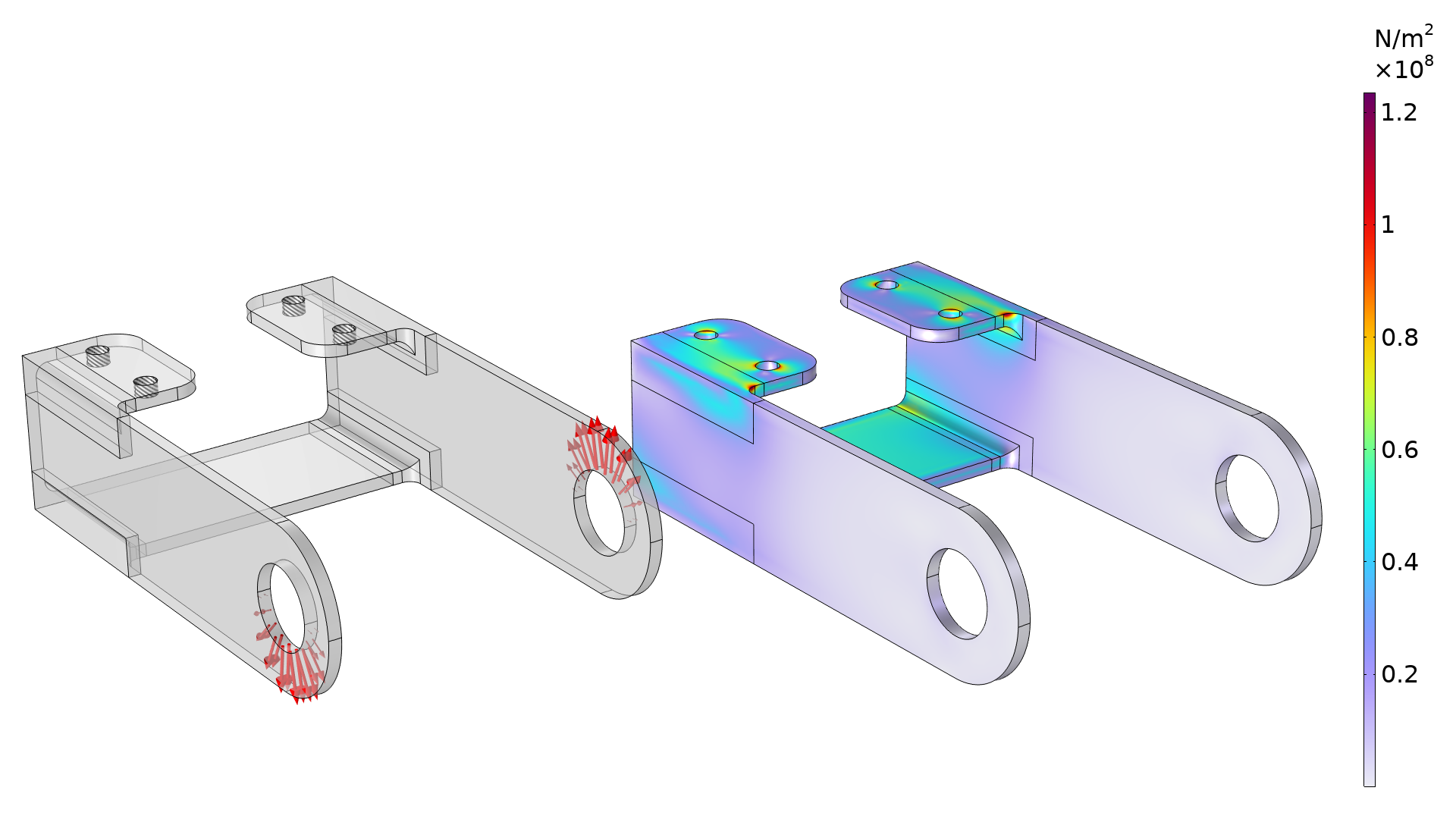
プロットは境界条件(左)と初期応力分布(右)を示しています. 応力はブラケット上部のフィレット付近に集中しています.
最適化では, 目的関数として前のセクションで述べたpノルム (p=50) を使用しますが, より重い, または剛性の低い構造を避けるために制約も追加されます. ここで検討している 3D サンプルでは自由形状境界機能を使用していますが, ブログ “電磁気学における形状の最適化: パート 1”で説明されているように, COMSOL Multiphysics® ソフトウェアには形状最適化のための他のさまざまな機能が組み込まれています. 自由形状境界機能を使用すると, 問題のあるフィレットの形状が変更されて応力集中が軽減され, 疲労特性が改善されます(下図).
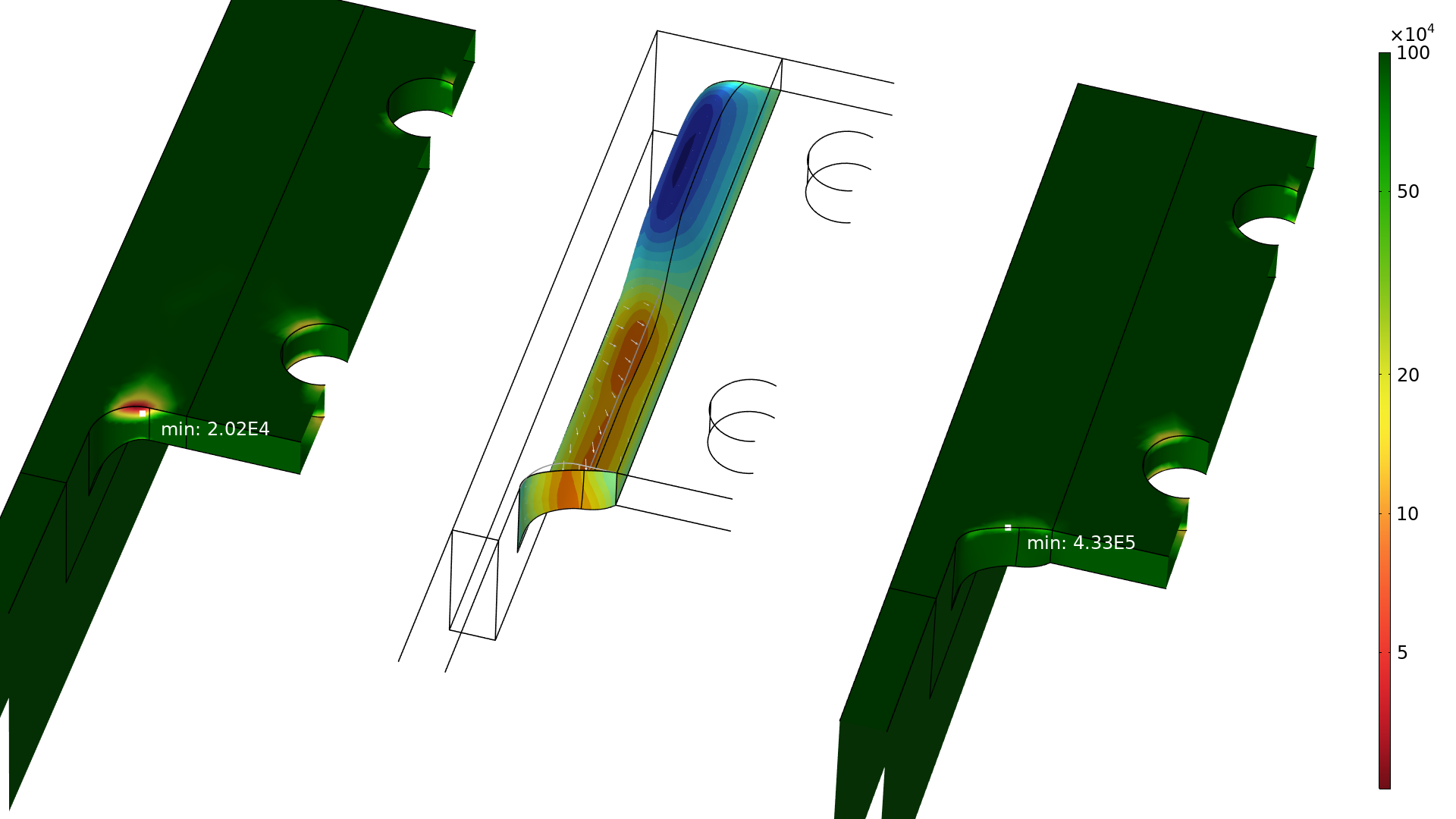
初期設計と最適化設計の切り抜き(それぞれ左と右)について, 破損までのサイクル数をプロットしました. 中央の切り抜きでは, 青と赤の部分がそれぞれ材料の除去と追加に対応し, 形状の変化も矢印で示されています.
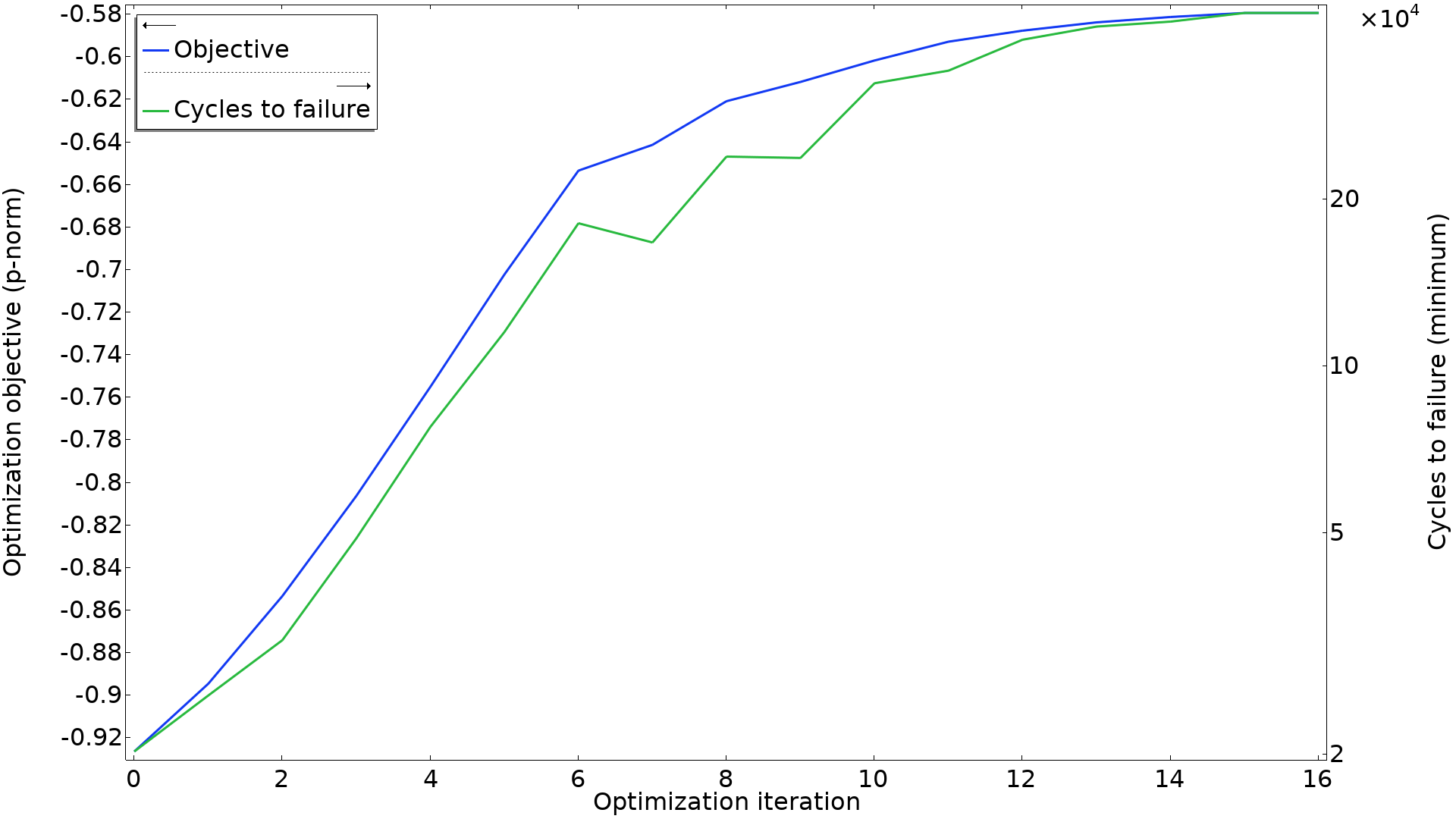
一般的に, 部品はそのどの部分であっても疲労寿命を超えると破損するため, 最も関連する数値は破損までの最小サイクル数です. 理想的には, これを直接目的関数として使用したいところですが, 下のグラフに見られるように, この数値とpノルム目的関数の間には良い一致があります.
pノルム目的関数値が破損までの最小サイクル数とともにプロットされています. いくつかの反復は, 破損までの最小サイクル数を改善することなくpノルムを改善しますが, 両者の間には良い相関がみられます.
フォン・ミーゼス応力と疲労寿命
純粋なフォン・ミーゼス応力の最小化が疲労寿命の改善とこれほどよく相関していることは, どのように説明できるのでしょうか?部品の疲労寿命は多くの要因に影響されますが, 応力範囲がその主な要因です. また, 平均応力にも強く影響されます. 荷重が完全に逆転している一般的なケースでは, 平均応力はどこでもゼロです.
通常, 疲労き裂は応力が集中する自由表面で発生します. 自由表面では平面応力状態が支配的ですが, 実際には応力状態がほぼ一軸であることが一般的です. これは, 例えば第一主応力とフォン・ミーゼス等価応力が同じになることを意味します.
平均応力を与える静的荷重ケースと脈動荷重を与える別の荷重ケースが混在している状況では, このアプローチは必ずしも最適ではないかもしれません. しかし, その場合でも, 応力集中部では, 異なるタイプの外部荷重が同様の応力パターンをもたらすことが一般的であるため, 成功する可能性は大いにあります.
ホイールの結果
2つ目の例として, ホイールリム – 疲労評価による応力最適化モデルからホイールリムを取り上げます. このモデルは, 4つの点を除いて, ブラケットと概念的に同じです:
- 複数の荷重ケースがあり, 疲労解析では(フィンドレー基準を用いて)最悪の組み合わせを探索するため, 最大応力との関係は弱くなると予想されます.
- 負荷ケースが増えるということは, 制約が増えるということでもあります.
- セクター対称性は, 形状の最適化のために設定されたもの(物理学的なものではない).
- 結果には(疲労寿命の代わりに)疲労使用率が使用され, これは相互安全率と考えることができます.
ホイールの形状, 制約, および境界条件を以下に示します. ボルトには単純な固定境界条件が使用されていますが, これは人為的な応力集中を引き起こすため, これらの領域は疲労解析から除外されています.
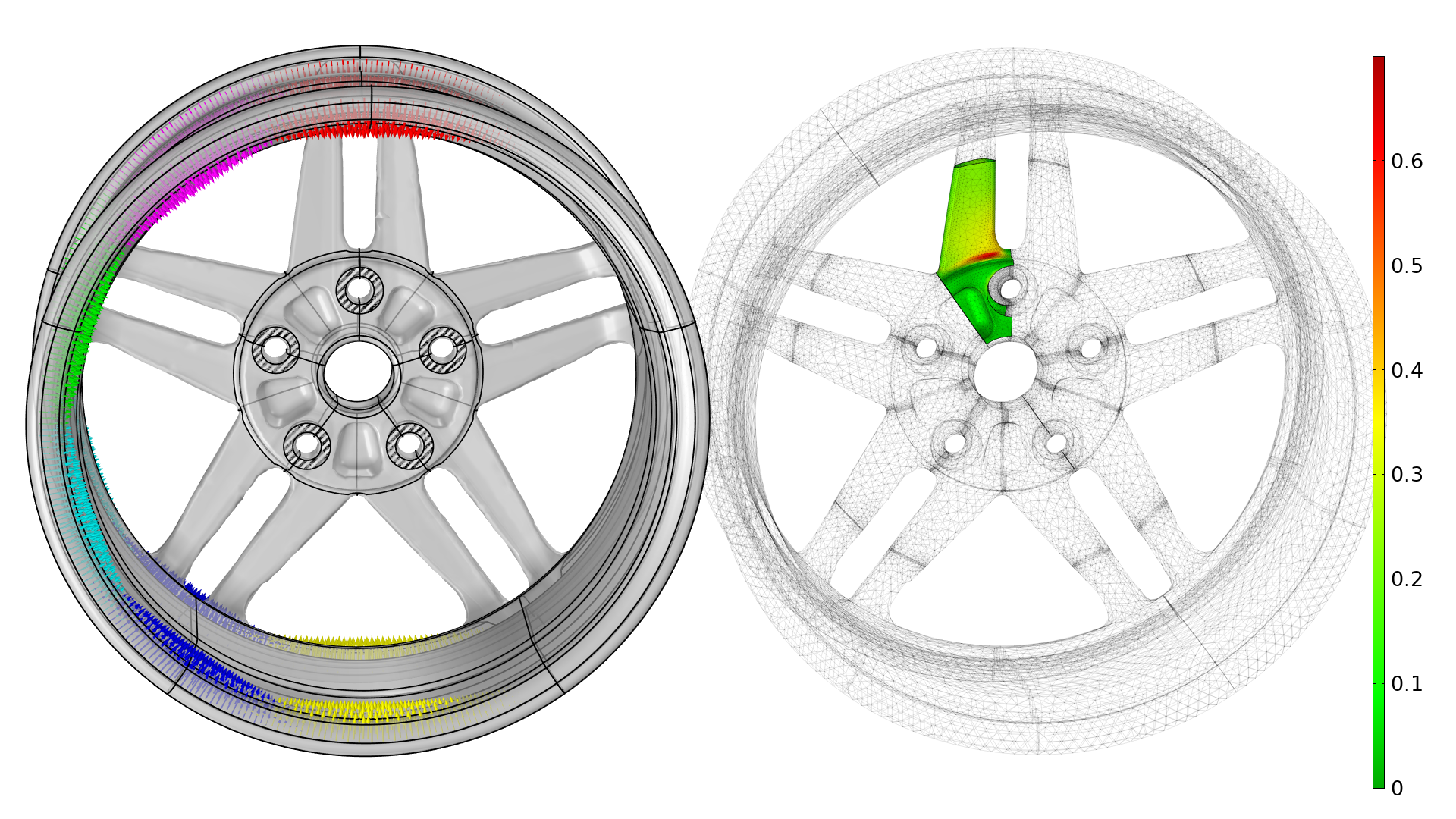
異なる荷重ケースを異なる色の矢印で示しています(左). このプロットは, ホイールの全回転に対応するすべての荷重ケースを考慮したものです. スポークには粗いメッシュを使用することができますが, 疲労や応力の評価には使用しないことに注意してください. ホイールにはタイヤの空気圧による負荷もかかりますが, これは図から除外しています.
最適化では, 質量に対する制約とともにp-ノルム目的関数 (p=20) を依然として使用しますが, この例ではより多くの荷重ケースを考慮するため, より多くの制約があります. 下図は, 最適化によってフィレットを修正することで疲労寿命がどのように改善されるかを示しています.
初期設計と最適化設計の切り抜き(それぞれ左と右)について疲労使用率をプロットしたもの. また, 中央の切り抜きでは形状の変化を矢印で示し, 灰色と黒色の線はそれぞれ初期形状と最適化形状を示しています.
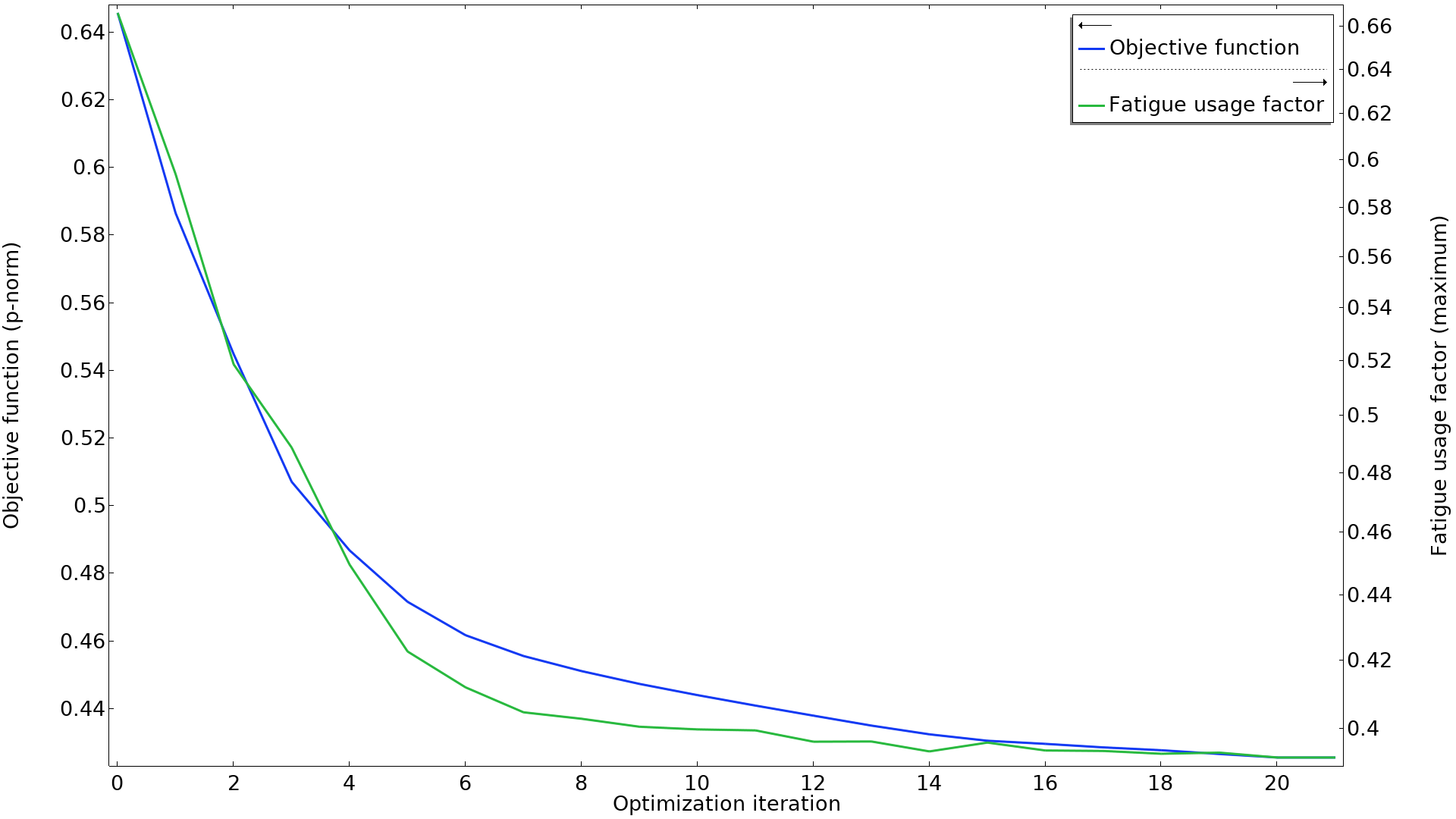
この例では, 下のグラフに見られるように, pノルム目的関数と破損までの最小サイクル数との間にも良い相関関係があります. 注目すべきは, 2つの荷重ケースがpノルムの点では優勢ですが, すべての制約が最適化を通して有効なままであることです.
pノルム目的関数値が最大疲労使用率とともにプロットされています. この2つの曲線はよく相関しています. 疲労使用率が対数軸上にプロットされていることに注意.
まとめ
疲労寿命の最適化は一筋縄ではいきませんが, 応力ベースの形状最適化によって挙動を改善できることがよくあります. 最適化の結果は, 疲労解析でチェックする必要があります. その後, 最適化結果をワークフローの次のフェーズのインプットとして使用することができます.
このブログでは, フォン・ミーゼス応力のpノルムを目的関数として使用することに焦点を当てましたが, COMSOL Multiphysics®は勾配ベースの最適化に必要な感度分析を自動的に実行しますので, 別の目的関数を試すことは簡単です.




コメント (0)