
Named after Plato, Platonic solids are regular, convex polyhedra that consist of the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. This well-known quintet has been studied since time immemorial due to their attributes and historical significance. As of version 5.5 of the COMSOL Multiphysics® software, the Platonic solids are available in the Part Library. In this blog post, we look into the story behind Platonic solids and show how to create a dodecahedron defined by the radius of the inscribed sphere.
Platonic Solids: A Historical, Geometrical, and Modern Point of View
Born in Athens around 430 B.C., Plato became one of the most famous philosophers of all time. As a student of Socrates and teacher of Aristotle, he founded the science-focused Academy (commonly referred to as the first Western university) and contributed to philosophy with iconic works like The Republic. In Timaeus, Plato unraveled the mystery of the four classical elements, connecting each element to a solid that is similar to the shape of their atoms. Fire is associated with the tetrahedron, earth with the cube, air with the octahedron, and water with the icosahedron. Lastly, the dodecahedron is considered to represent the constellations that make up the universe. Ever since then, this well-known collection of polyhedra has been called the Platonic solids.
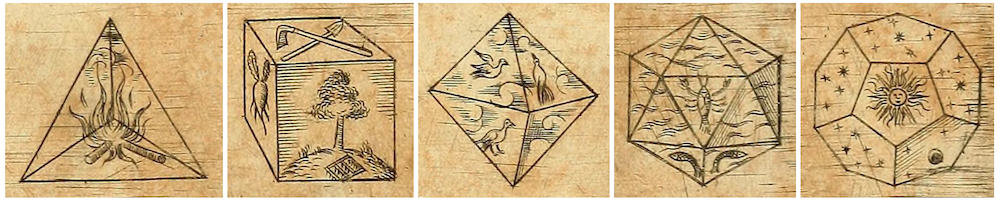
The Platonic solids with their respective elements, as drawn by Johannes Kepler in Harmonices Mundi from 1619. From left: tetrahedron, cube, octahedron, icosahedron, and dodecahedron. Images in the public domain, via Wikimedia Commons.
The Platonic solids are characterized as three-dimensional, convex, and regular solid objects. They have identical polygonal faces with respect to shape, size, angles, and edges, and an equal number of faces meet at every vertex. Only the tetrahedron, cube, octahedron, dodecahedron, and icosahedron satisfy these requirements. The names of the Platonic solids are based on the number of faces each solid consists of.
Following their symmetrical properties, it is possible to create different combinations of a Platonic solid and a sphere, specifically circumscribed spheres, inscribed spheres, and midspheres. A circumscribed sphere is a sphere with a radius such that the created Platonic solid fits perfectly inside. On the contrary, the sizes of an inscribed sphere and a midsphere are chosen such that they fit inside. The faces of the inscribed sphere are tangent to each face of the Platonic solid, while the faces for the midsphere are tangent to the edges of the Platonic solid. An example of an inscribed sphere is shown in the last image.
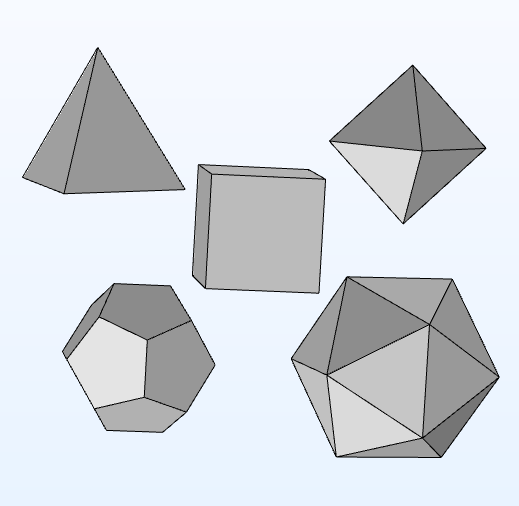
The complete collection of Platonic solids: tetrahedron (top left), cube (middle), octahedron (top right), dodecahedron (bottom left), and icosahedron (bottom right).
Apart from their natural beauty, many interesting uses of Platonic solids exist in technology. For instance, tetrahedrons are frequently applied in electronics, icosahedrons have proven to be useful in geophysical modeling, and speakers with polyhedral faces are used to radiate sound energy in all directions. Although the dodecahedral variant seems to be more established in room acoustics measurements as omnidirectional sources of sound, a tetrahedron loudspeaker can, under certain circumstances, have better radiation uniformity.

A dodecahedron hangs from the roof of the Tekniska Högskolan metro station near the Royal Institute of Technology in Stockholm, Sweden. Image by Arild Vågen — Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.
Now, let’s look at how you can model a dodecahedron with an inscribed sphere in the COMSOL Multiphysics® software.
Modeling a Dodecahedron with an Inscribed Sphere from the Part Library
As of COMSOL Multiphysics® version 5.5, you can choose between four variants of the specific Platonic solid, depending on which parameter is most relevant.
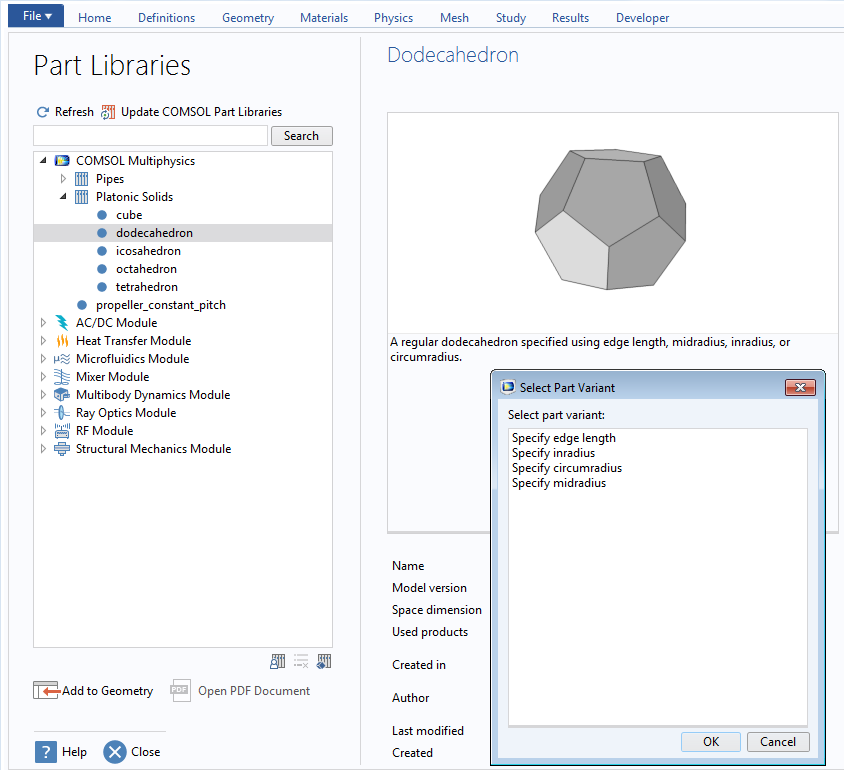
The Platonic solids are found under COMSOL Multiphysics in the Part Libraries. The part variants to choose from give the possibility to specify edge length, inradius, circumradius, or midradius.
Adding the inradius part variant to the geometry will generate a dodecahedron with the default expression for the inradius given as sqrt((25+11*sqrt(5))/10)/2, centered at the origin. This expression will automatically give an edge length of 1 m. You can easily change the input parameter, work plane, displacement, and rotation in the Settings window to create a customized dodecahedron. The image below shows an example of a dodecahedron where the inradius is set to 1[m]. The side length of the dodecahedron is automatically calculated based on the expression for the inradius.
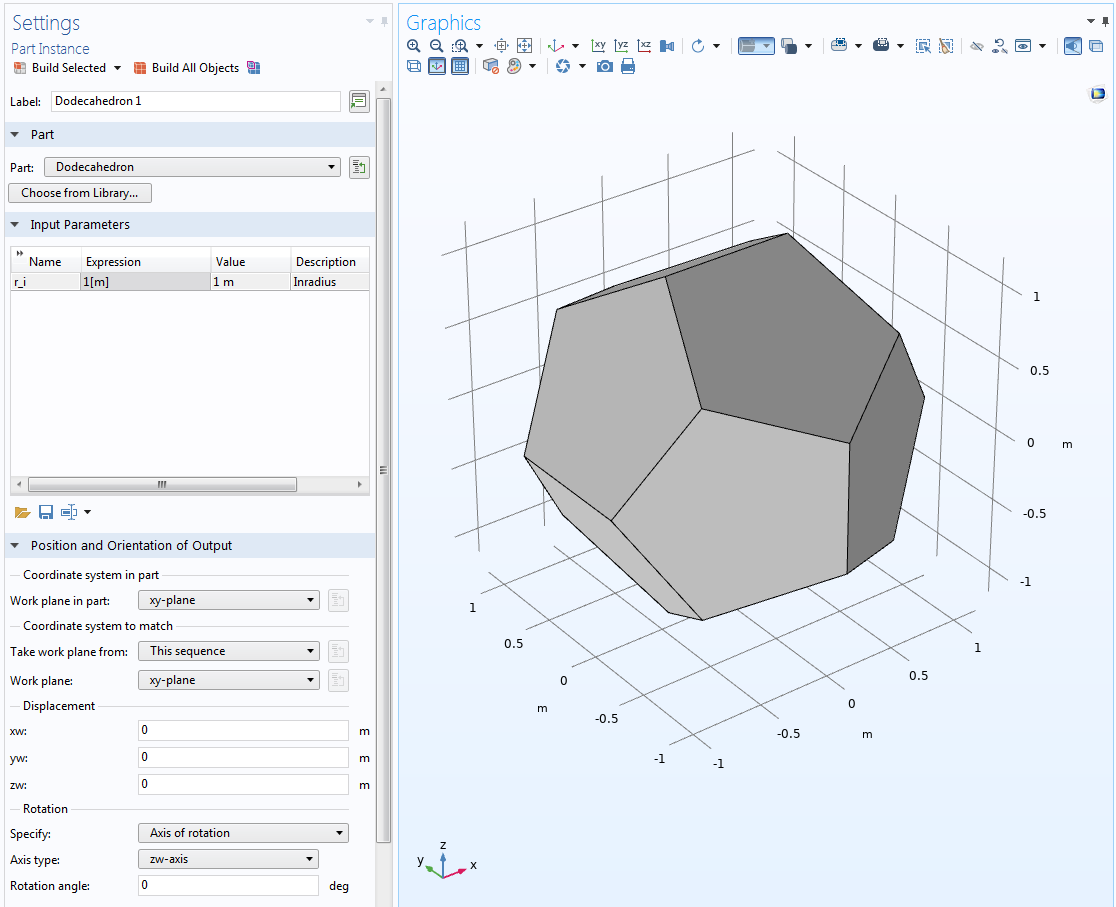
You can change the inradius, work plane, displacement, and rotation of the dodecahedron.
Now, let’s construct a sphere within the dodecahedron; i.e., an inscribed sphere. You can adjust the properties suitably to position the sphere inside of the Platonic solid and make sure that the inradius and the radius of the sphere are equal.
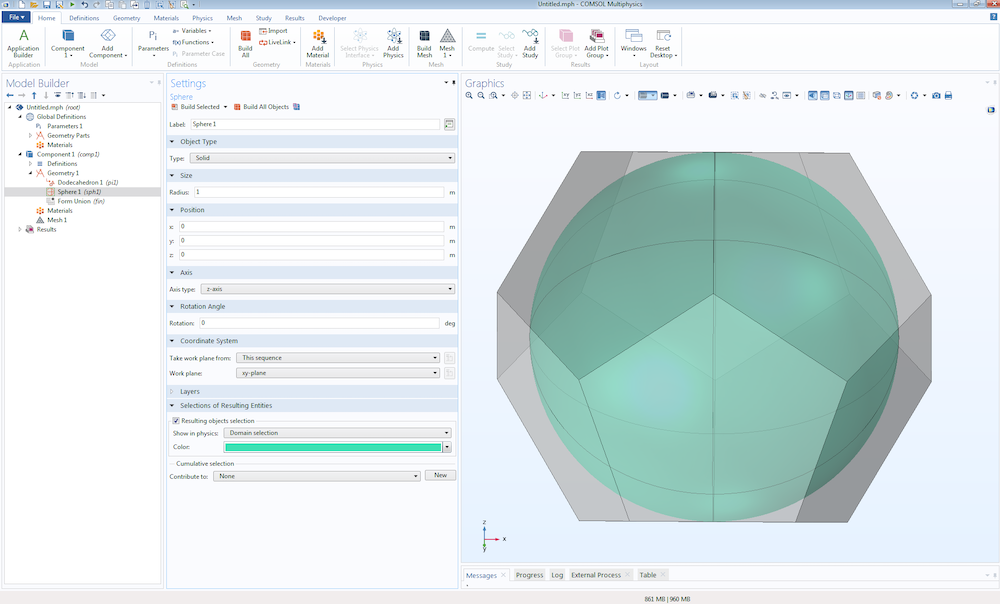
An inscribed sphere is created by adding a sphere to the geometry.
Learn More About Building Geometries in COMSOL Multiphysics®
Whether it concerns building a complex geometry for a simulation or studying the Platonic solids for educational purposes, there are plenty of possibilities with these built-in parts and their functionality. The Part Library in COMSOL Multiphysics also contains other useful parts that can simplify your simulations, some of which are specific to the add-on modules. It is also possible to create your own parts and add them to a user-defined Part Library, as shown with an example in the blog post Using Geometry Parts and Part Libraries in COMSOL Multiphysics®.
Take a look at these additional resources for more information about creating geometries:





Comments (0)