A shift-and-weight method for fast interpolation of probe charge electrostatic potentials
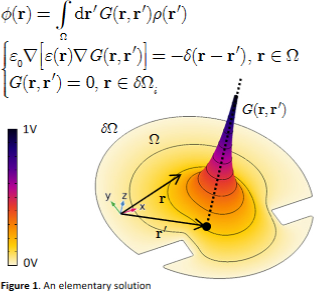
The Poisson equation, as implemented in the COMSOL Multiphysics® AC/DC module, solves for the electrostatic potential due to general charge distributions subject to various boundary conditions, very often Dirichlet conditions of constant potential at conductor surfaces. When both the charge distribution and the boundary conditions are fixed, finding the PDE solution with COMSOL Multiphysics® ’s electrostatic interface, is the most straightforward and efficient way. However, if the boundary conditions or the charge distribution vary, then using a primitive solution approach, also known as the Green’s functions method, which takes advantage of the linearity of the Poisson PDE, may prove more advantageous. This situation is often encountered with semiconductor electronic devices, whose terminal voltages are not fixed, and where the charge distributions within the semiconductors are unknown and have to be solved for iteratively from a Poisson-Schrödinger (or approximations thereof) system of PDEs. Iterating over 3D Poisson solution may prove very costly, and the aforementioned Green’s function approach can significantly accelerate (~ x100) and stabilize the computation, as we showed in a previous contribution to the COMSOL® conference in Rotterdam. The core innovation in that work was a method, labelled the “warping method”, capable of fast and accurate interpolation of the electrostatic potential of a test probe charge from the precomputed electrostatic potentials of two other probe charges bracketing the test charge. Bracketing here means that the test and two probe charges are collinear and the test charge is in between the probe charges. In this work we extend and generalize the “warping method” by a-similar-yet-essentially-different interpolation method, the “shift-and-weight method”, who is now able to deal with non-collinear probe charges, and any number (>1) of such probe charges in any 3D arrangement, provided the convex hull of the probe charges contains the test charge. This new method, will make the Green’s function approach to Poisson’s problem much more generally applicable. The main idea of the “shift-and-weight method” is utilizing a modified Laplace equation to compute a displacement (shift) field, which subsequently is utilized to shift the potential of any probe charge from its location to the position of the test charge. The shifting itself is implemented in COMSOL Multiphysics® via a generalized extrusion, and is similar in spirit to the moving mesh idea. Within the constellation of the probe charges, each precomputed electrostatic potential is first shifted to the position of the test charge and then weighted based on their relative distance to the test charge, with the furthest probe charges contributing less than the closer ones. In this presentation, we will introduce the method with illustrative examples and assess its performance in terms of accuracy and speedup.
ダウンロード
- poster.pdf - 0.33MB
