ラーニングセンター

Supplement A: More on the Advantages of Swept Meshing

---

For a swept mesh, there are three major advantages:

1. Using it results in a lower number of mesh elements.
2. Prisms and hexahedra are typically more robust for thin geometries.
3. It is efficient to generate.

Let us go through each advantage in more detail.

Low Number of Mesh Elements

For any type of volume mesh that is homogenous in size (i.e., all elements have the same size), the number of elements, , is proportional to the total volume to be meshed, , and inversely proportional to the cube of the typical mesh size, :

This constant of proportionality is of interest to us. It can be shown that for a given mesh size and volume:

• A prism mesh will consist of 1/7 of the amount of elements as a tetrahedral mesh.
• A hexahedral mesh will consist of 1/17 of the amount of elements as a tetrahedral mesh.

In reality, the mesh is almost never homogenous because of refinements due to the geometric complexities, but this gives a good order of magnitude.

The number of elements used to discretize a model domain affects the computational time and resources required to solve the model equations. However, this number alone is not really what matters when performing a study; the number of degrees of freedom (DOFs) is the governing number. For example, solving for the temperature field (using the energy conservation equation) means solving for a single DOF per computational point, whereas solving for solid mechanics means solving for at least three variables per computational point, which requires increased computational time and resources (when we use comparable solving strategies). Additionally, if the problem is nonlinear, we may find ourselves solving for a problem iteratively, resulting in an even more time- and resource-consuming simulation.

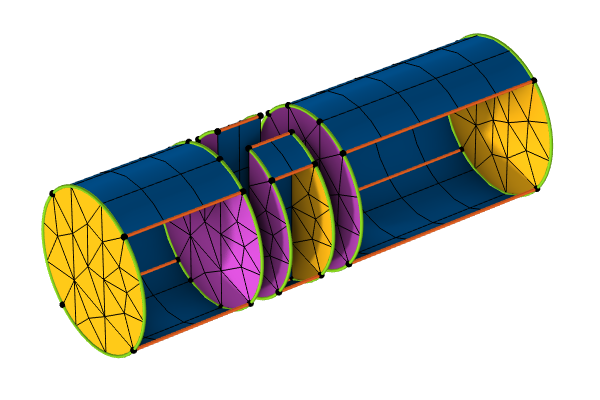
The placement of the element nodes for the three most common discretization types (linear, second-order Lagrange, and second-order serendipity) is depicted in the animation below:

Placement of the second-order Lagrange element nodes for different volume mesh elements (red, black, and blue points). If we remove the blue nodes, we obtain the corresponding serendipity elements. The linear element nodes are depicted with red points; they correspond to the mesh vertices.

Notice that for any of the three discretization types, prism and hexahedron elements contain more DOFs per element, but this is compensated by the fact that there are less elements in total in a swept mesh. Overall, the net gain is lower than the one we could have hoped for after comparing the number of mesh elements, but this is still significant. Notice also that a tetrahedral element with serendipity discretization has the same number of DOFs as a tetrahedral element with Lagrange discretization. This means that the net gain of swept meshes with serendipity discretization is even more significant.

It can be shown that a homogenous mesh composed of prisms or hexahedra, compared to a homogenous mesh composed of tetrahedra with same discretization and size, requires:

• Around 1/2 the number of DOFs, using linear or quadratic Lagrange discretization
• Around 1/4 the number of DOFs, using quadratic serendipity discretization

Robust Types of Elements in Thin Geometries

Throughout this section and course, we should keep in mind that the quality metrics are more of a hint of what matters for a simulation than something that is absolutely known. The interpretation of this measure will depend on the model and the type of physics being solved. Because of this, when we write that a mesh is "good", this means that the user followed the field guidelines and the current state-of-the-art in mesh quality.

Good element quality is something we should strive to achieve, as this quantity influences the robustness of the numerical problem. As a rule of thumb, the mesh should result in a well-conditioned stiffness matrix. (The mesh quality is a good indication of this.) A broader discussion on what constitutes a quality mesh is outside the scope of this course, but is one of the fundamental topics of numerical analysis.

The mesh should have the lowest number of elements, yet use a sufficient amount to still be accurate enough to provide reliable solutions. The mesh elements should also be of good quality, as higher-quality meshes provide better convergence. Note that these properties are in general conflicting and require you to use your own engineering judgement to decide on what is the best compromise between them.

Prisms or hexahedra, which compose a swept mesh, can be of good skewness quality even when the element is very flat. In other words, they can be stretched or compressed along one direction, and their skewness quality will not be impaired, unlike with tetrahedra.

From left to right: a tetrahedron, prism, and hexahedron mesh element are being vertically compressed from an optimal shape (all length equal) to a flat version.

Other types of quality measures (such as volume versus length) report a low mesh quality — even for swept elements — because those measures take the aspect ratio (ratio between the longest and smallest length) into account. With this, it seems that we arrive to a contradiction. So, what is the quality measure to "trust"? It depends.

In a general case, the ratio between largest and smallest coefficients of the stiffness matrix are proportional to the square of the aspect ratio. In other words, the matrix can become ill-conditioned for elongated elements. From a physics point of view, swept meshes with a high aspect ratio should not be used in case the solution field has a strong cross gradient (a gradient diagonal to the element, which is not uncommon in most solid mechanics problems) because the solution might not converge or be accurate.

However, for other particular fields being solved, it might happen that the cross gradient is negligible. In that case, the skewness quality is a good indicator to follow (remembering that the prism and hexahedron elements keep a high value). Consequently, this means that a swept mesh enables us to use fewer elements, and less DOFs, while keeping the solution robust.

Swept Mesh Elements on Thin Geometries

Let us suppose that the physics can use a mesh with elongated mesh elements. There are two cases of scenarios to consider.

This first scenario is for elongated geometries, such as cables and pipes. You would need to create a swept mesh with elements that are more or less stretched along the length of the geometry. Say, for example, that the aspect ratio of the swept mesh element is , and the number of DOFs is less compared to tetrahedra. ( for serendipity discretization.)

Two stacked elbow pipe geometries with different meshes.

Comparison between two types of meshes for an elbow pipe geometry. The swept mesh (at the top) is composed of prisms with a length twice as long as their base (hence why ). Compared to prisms with an aspect ratio of 1, this mesh has consequently around 2 times less DOFs if it is discretized with quadratic Lagrange elements. Overall, the swept mesh has 4 times less DOFs compared to the tetrahedral mesh (at the bottom).

The second scenario is for narrow geometries (plate-like geometries with a small thickness). For such geometries, the effect is even more noticeable. To be isotropic, the tetrahedra need to have at least the size of this small thickness, while swept elements can be large on the perpendicular directions of the sweep. For an aspect ratio, , of the swept mesh elements, the number of DOFs are now lower! ( lower for serendipity discretization.) This principle is also used when resolving high fluid velocity gradients near walls using a boundary layer mesh.

Comparison between two type of meshes for a resonator geometry, with each geometry zoomed in on a corner. The left image shows this geometry with a swept mesh using prism elements, whereas the right shows the geometry with an unstructured free tetrahedral mesh. In both cases, the meshes are resolving the depth with the same number of elements. However, the prisms have an aspect ratio of 50. This means that there are 2500 times less elements on the surface. Overall, this means that the mesh on the right would use around 5000 times more DOFs.

Efficient to Generate

In comparison with the tetrahedral mesher, where the insertion of interior nodes might take a long time for large meshes due to the fact that it is unstructured, a swept mesh is relatively quick to generate because it essentially only needs to mesh the boundaries, as the interior nodes are deduced automatically. This is a simplified explanation to fit the scope of this article. However, even though the mesh generation is faster, it might also necessitate further geometric operations in order for the geometry to be "sweepable". This part usually requires additional time that cannot be neglected in some cases.

Example

If used appropriately, swept meshing allows the meshing of different designs to be completed faster and require less resources in terms of RAM than other types of meshes, making our solution and overall product development process faster and leaner. The main takeaway is that, with this type of mesh, we can decouple the mesh discretization perpendicular to the sweep direction with the discretization along the sweep direction, which can be useful in many situations, as demonstrated below with the Surface Micromachined Accelerometer tutorial model. MEMS is a typical application where swept meshes are useful since they exhibit high aspect ratios.

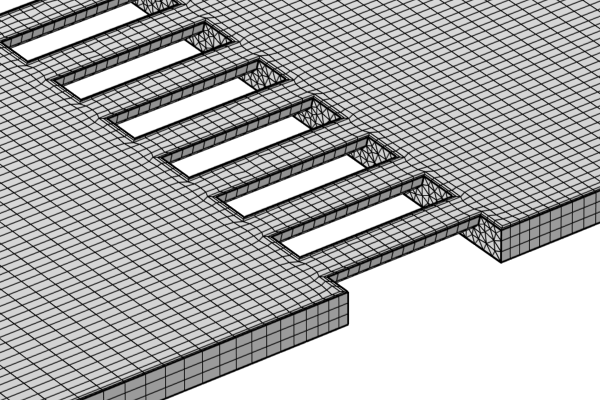
The geometry for the Surface Micromachined Accelerometer.

The model geometry for the Surface Micromachined Accelerometer tutorial model. The top air domains are hidden for visual purposes.

The default tetrahedral mesh generated for the model geometry uses over 120,000 elements, whereas a swept mesh with prism elements contains little over 30,000 elements — a significant difference. There are more elements in the swept mesh than the theory predicts due to the specifics of the topology in this particular geometry. In terms of DOFs, the swept mesh uses 1.3 times less than the default one. The swept mesh also has a higher minimum element quality than the default, unstructured mesh above it.

The default tetrahedral mesh for the Surface Micromachined Accelerometer tutorial model (left) with the size for the elements set to Normal. The swept mesh for the same geometry (right) contains significantly less elements.