一般 Blog Posts
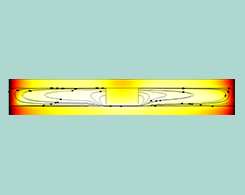
時間に依存する問題における時間ステップと次数の自動選択
ここでは, COMSOL Multiphysics® の時間依存ソルバーログを紹介し, 離散時間ステップスキームの理論と最適な時間ステップおよび離散化次数について詳しく説明します.
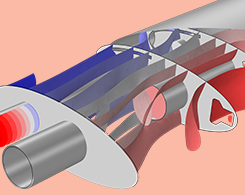
音響導波管モデルでのポート境界条件の使用
複数のポート境界条件を組み合わせることで, 排気系とマフラーシステムの透過損失と挿入損失を簡単に計算できます. 音響モデリングにおけるこの機能のその他の利点をご覧ください.

デジタルツインとモデルベースの電池設計
エンジニアは, 高忠実度のマルチフィジックスモデルと軽量モデルおよび測定データを組み合わせることで, デジタルツインを作成し, 現実世界のシステムを理解, 予測, 最適化, 制御できます.
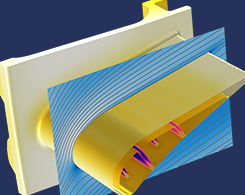
デジタルツイン: 単なる誇大宣伝ではありません
“デジタルツイン” という用語は, 単なる誇大宣伝から革命的な概念まで, さまざまな呼び方をされてきました. ジェットエンジンの例を使用して, デジタルツインの概念とシミュレーションがどのように適合するかを説明します.

FEMとFVMの比較
有限要素法, 有限体積法, あるいはハイブリッドなアプローチ. CFDにはどれが最適なのでしょうか?それは, 求解しようとしている流体の流れの問題によります.

共役熱伝達モデリングにおける不連続メッシュの使用
COMSOL Multiphysics® では, 隣接するドメインで異なる不連続メッシュを使用できます. この機能は, 特に共役熱伝達問題をモデル化する場合に役立ちます.

製造プロセスのシミュレーションで材料をアクティベートする方法
溶接や積層造形などの製造プロセスをモデル化していますか? 特殊な機能を使用して, 材料堆積シミュレーションで材料をアクティブ化または非アクティブ化できます.

COMSOL® で移動荷重と制約をモデル化する3つのアプローチ
COMSOL Multiphysics® で移動荷重と制約をモデル化する3つの方法 (変数, 補間関数, CAD ジオメトリからインポートしたパスの使用) を学びます.

Chladni 板はどのようにして音を可視化できるようにするのですか?
音を見ることは可能ですか? Chladni 板の背後にある音響に関するこのブログで, ご自身で確かめてください.

COMSOL Multiphysics® のクラスタースイープノードの使用方法
COMSOL Multiphysics® のクラスタースイープノードを使用して, クラスター上のパラメトリックコンピューティングの並列化を最適化し, クラスター管理者の負担を軽減します.
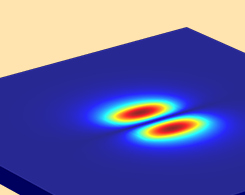
COMSOL Multiphysics® を使用して光学異方性媒体をモデル化する方法
Erasmus Bartholinus 教授は, 1669年に複屈折の光学効果を初めて観察しました. 今日では, 光学異方性媒体に特化したモデリング手法を使用してこの効果を観察できます.
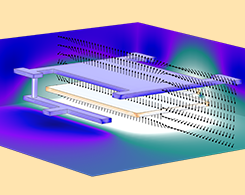
ワイヤー, 表面, および固体を使用して静電気モデルを作成する方法
AC/DC モジュールで利用可能な境界要素法に基づく静電気機能を使用して, ワイヤー, 表面, および固体を組み合わせたモデルを構築するためのガイドです.

計算された解をフーリエ変換する方法
この波動光学のデモンストレーションでは,フレ ネルレンズの電磁シミュレーションを例に, 計算された解に対するフーリエ変換の実装方法を学びます.
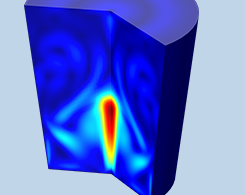
COMSOL Multiphysics® での自然対流のモデル化の概要
電子機器の冷却, 室内気候システム, 環境輸送の問題はすべて自然対流に依存しています. COMSOL Multiphysics® でこの現象をモデル化する方法を学びましょう.
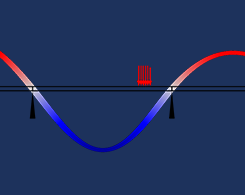
シミュレーションで境界条件を条件付きにする方法
モデリングシナリオによっては, 境界条件を幾何学的境界の一部または特定の条件下でのみ適用したい場合があります. その方法については, こちらを参照してください.

COMSOL Multiphysics におけるフーリエ変換の実装方法
フラウンホーファー回折の例を用いて, COMSOL Multiphysicsにフーリエ変換を実装する方法をご紹介します.

パート 2: ユーザーワークフローを強化するためのシミュレーションアプリの設計ヒント
シミュレーションアプリのユーザーインターフェースを設計して, アプリのユーザーにとってより直感的で効率的なものにするためのヒントとコツをいくつか紹介します. 2部構成のシリーズのパート2.
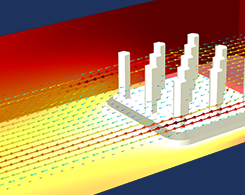
パート 1: シミュレーションアプリの設計と構造を改善するためのヒント
ここでは, 明確で合理化された設計と構造を持つシミュレーションアプリを作成するのに役立つアプリケーションビルダーのガイドラインをいくつか紹介します. 2部構成のシリーズのパート1.

アプリを使用した周波数領域での磁性材料のモデル化
有効な非線形磁性曲線計算機シミュレーションアプリを使用して, B-H 曲線または H-B 曲線を有効な B-H 曲線または H-B 曲線に簡単に変換できます.

パート 2: 一般押出し演算子による変数のマッピング
非線形マッピングと異なる次元のジオメトリエンティティ間の変数のマッピングを処理するように設計された一般押出し演算子の使用方法を学習します. パート 2/2.
シミュレーションアプリを使用してバイオセンサー設計でバイオを感知する
バイオセンサー設計デモアプリは, この分子の酵素への付着を理解し, 生体分子の濃度 (または活性) の測定結果を予測します.

波動電磁気学における完全整合層と散乱境界条件の使用
散乱境界条件と完全整合層を使用して波動電磁気学問題のドメインを切り取る方法と, 問題のモデリングシナリオに最適な手法を学びます.

シミュレーションアプリでのジオメトリモデリング
パラメーター化された CAD モデルに基づいてジオメトリをモデル化するために使用できるシミュレーションアプリを作成するときに, 累積選択とジオメトリパーツを使用する方法を確認してください.

管状反応器の数学的モデリングを指導するためのアプリ
化学工学の学生は, 管状反応器アプリを使用して非理想的な管状反応器をモデル化し, さまざまな動作条件の影響を調べることができます. 詳細はこちら >>
