たとえば, シミュレーション中に荷重がさまざまなメッシュ要素や境界を横切るように移動するモデリングケースに取り組んでいるとします. このような場合, 特に, 境界条件を幾何学的境界の一部のみに適用したり, 特定の条件下でのみ適用したりしたい場合があります. このブログでは, COMSOL Multiphysics の柔軟性を活用してこのような状況に対処する方法について説明します.
境界条件の分類
偏微分方程式の数学的処理では, ディリクレ, ノイマン, ロビン タイプの境界条件に遭遇します. ディリクレ条件では, 解く変数を指定します. 一方, ノイマン条件は, 流束, つまり従属変数の勾配を指定するために使用されます. ロビン条件は, 前述の2つの境界条件タイプを組み合わせたもので, 変数とその勾配の関係を指定します.
次の表には, さまざまな物理学の分野から, 対応する物理的な解釈を示すいくつかの例が示されています.
| フィジックス | ディリクレ | ノイマン | ロビン |
|---|---|---|---|
| 固体力学 | 変位 | 牽引力 (応力) | バネ |
| 熱伝達 | 温度 | 熱流束 | 対流 |
| 圧力音響 | 音圧 | 法線加速 | インピーダンス |
| 電流 | 固定電位 | 固定電流 | インピーダンス |
有限要素法 では, これらのタイプの境界条件は, 求解する問題の構造にさまざまな影響を与えます.
ノイマン条件
ノイマン条件は “負荷” であり, 方程式の系の右側に表示されます. COMSOL Multiphysics では, 方程式ビュー で弱寄与として見ることができます. ノイマン条件は右側への純粋な加法寄与であるため, 時間, 座標, またはパラメーター値など, 変数の任意の関数を含めることができます.
半径 R の円形熱源が速度 v で x 方向に移動する熱伝達の問題を考えてみましょう. その強度は, ピーク値 q_0 を持つ放物線分布をしています. この負荷を数学的に記述すると, 次のようになります.
移動負荷の場合, 負荷分布に常に適合するドメイン境界やメッシュを持つことは明らかに不可能です.
負荷分布自体は簡単に入力できます. ラジアル座標の変数 r は2か所で使用されるため, 変数として定義することをお勧めします. 移動する熱源の入力全体を次に示します.
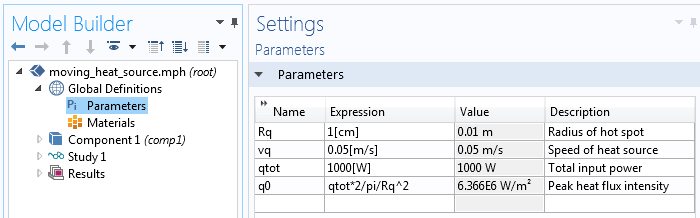
移動する熱源を表すパラメーター
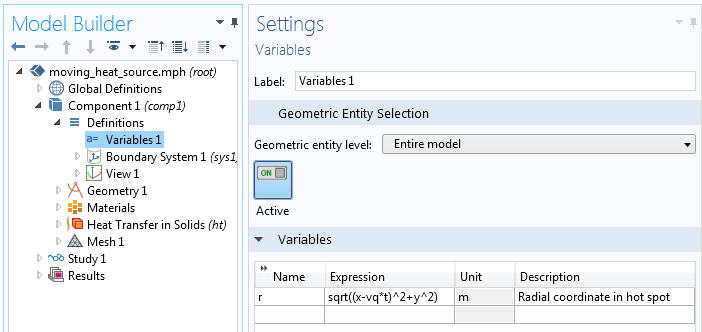
移動する熱源の現在の中心からのローカルラジアル座標を表す変数.
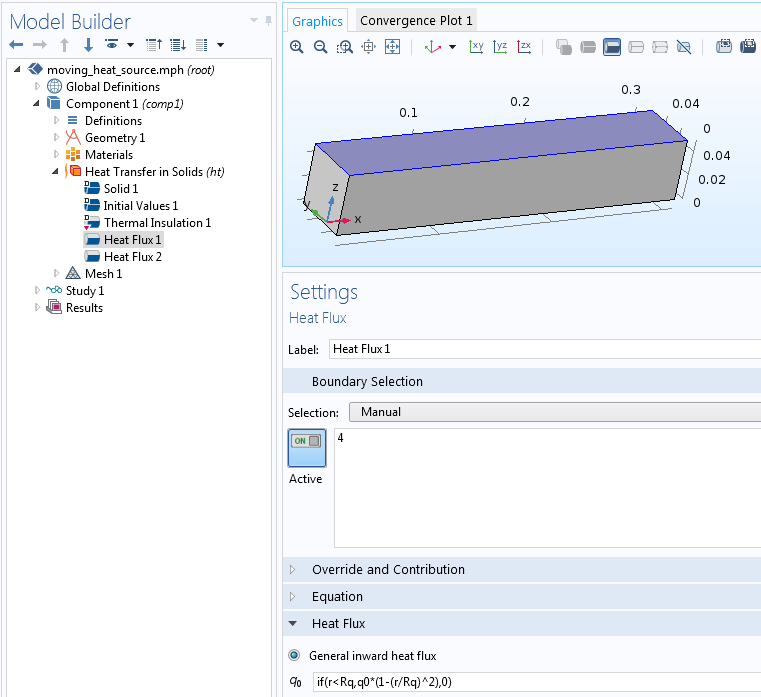
熱流束の入力.
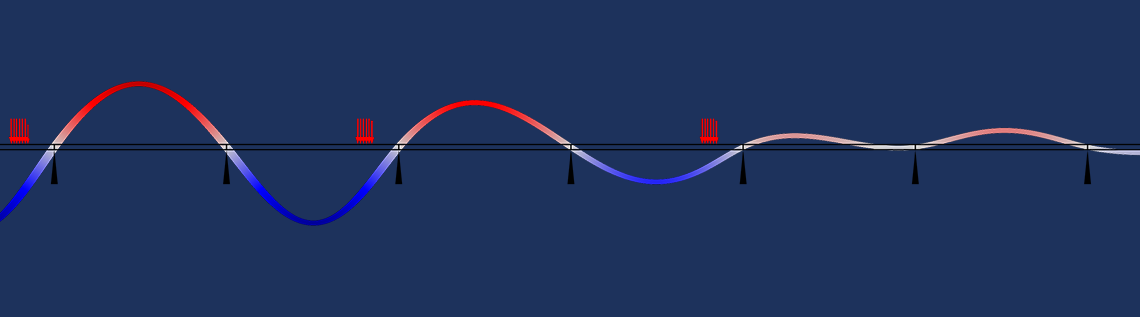
このようなデータを使用した時間依存シミュレーションの結果は, 次のアニメーションに示されています. yz 平面では対称性が想定されるため, 荷重は実際には移動する半円に適用されます.
熱源がバーに沿って移動するときの温度分布のアニメーション.
ディリクレ条件
ディリクレ条件が与えられている場合, 従属変数は規定されているため, それを解く必要はありません. したがって, このような自由度の方程式は問題から除外できます. したがって, ディリクレ条件は剛性行列の構造を変更します. COMSOL Multiphysics の 方程式ビュー を見ると, これらの条件は拘束として表示されます.
移動スポットの温度を正確に 450 K に規定するとします. これは少し不自然かもしれませんが, ノイマン条件とディリクレ条件の重要な違いを示しています. 温度 ノードを追加して, 同様の式 ( if(r < R,450[K],0)) を入力すると, ホットスポットで覆われていない境界部分の温度が絶対零度に設定されることになります.
ただし, ホットスポットの外側でディリクレ条件をオフにすることが目的です. これを行うには, ちょっとしたコツがあります. 代わりに, 規定値として if(r < R,450[K],ht.Tvar) を入力すると, 意図した動作が得られます (次のアニメーションを参照).
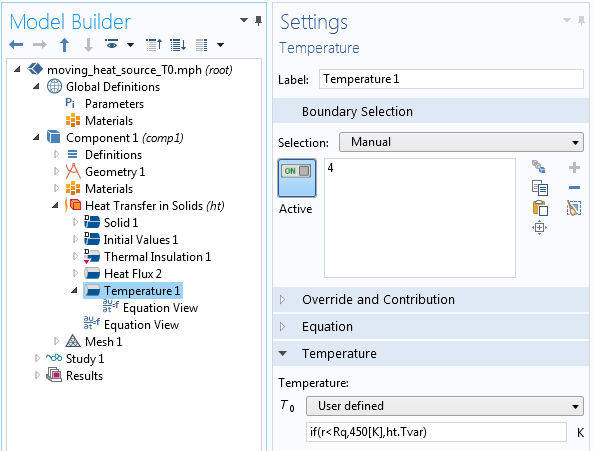
条件付きディリクレ条件の設定.
規定温度スポットがバーに沿って移動する際の温度分布のアニメーション.
これがどのように機能するかを理解するには, 方程式ビュー を有効にして, ディリクレ条件 (この場合は規定温度) の実装を確認します:
方程式ビューを有効にする.
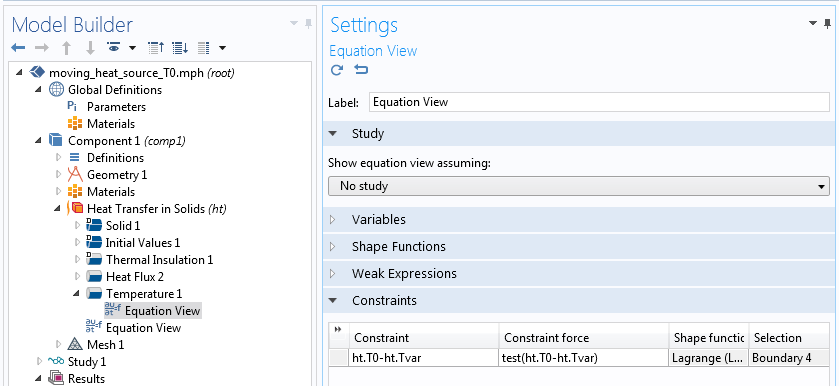
温度ノードの方程式ビュー.
拘束は ht.T0-ht.Tvar として定式化され, 暗示的的に ht.T0-ht.Tvar = 0 を意味します. 最初の項は規定の温度で, 入力として入力します. 2番目の項は, 変数に代入された温度の自由度です. これにより, 指定された値が文字列 ht.Tvar でない限り, 温度が指定された値と等しくなるように拘束されます. その場合, アセンブリ中のシンボリック代数によって式が ht.Tvar-ht.Tvar に縮小され, さらに 0 になります. 拘束式が 0 であるため, 拘束はありません.
弱拘束
COMSOL Multiphysics では, 実際にはディリクレ条件の2つの実装が可能です. デフォルトのケースは, 上で参照したように 点ごと拘束 ですが, 弱拘束 を使用することもできます. 弱拘束では, 方程式は削除されるのではなく追加されます. その後, 規定の温度値を適用するために必要な熱流束が, 追加の自由度 (ラグランジュ乗数) として追加されます.
基本的に同じトリックを使用して, 少し工夫するだけで, 弱拘束を条件付きにすることができます. 弱拘束を使用するには, まず 高度なフィジックスオプション を有効にする必要があります.
高度なフィジックスオプションを 有効 にする.
フィジックスインターフェース内のノードで弱拘束が選択されている場合, ラグランジュ乗数に自由度が追加されます. この場合, 自由度の名前は T_lm です.
上記と同じ温度の式を適用すると, ディリクレ条件がオフになっている境界部分では, 追加の自由度に剛性行列の寄与がまったくありません. 剛性行列は特異になります. この状況を回避するには, if(r < R,450[K],ht.Tvar) を if(r < R,450[K],ht.Tvar-T_lm*1e-2) に変更します. T_lm に使用される乗数は, さまざまなモデルや物理分野によって異なるため, 調整が必要になる場合があります.
これが機能する理由は, 教科書に書かれているように, “読者の課題として残されている” ためです.
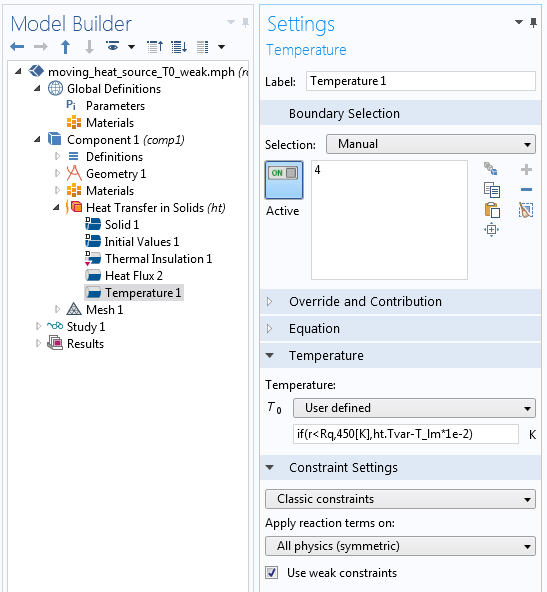
弱拘束を使用する場合の条件付きディリクレ条件の設定.
ロビン条件
ロビン条件は, 通常, 剛性行列と右辺の両方に寄与します. 剛性行列の構造は影響を受けませんが, 既存の位置に値が追加されます. ロビン条件は, 方程式ビュー にも弱寄与として表示されます. これらの条件を時間, 空間, およびその他の変数の関数に変換することは, ノイマン条件の場合と同じです.
ただし, 適切な値を選択することで, ロビン条件を近似的なディリクレ条件またはノイマン条件として機能するように変形できることは興味深いことです. これは, シミュレーション中に2つの境界条件タイプを切り替える場合に特に重要です.
ディリクレ条件を作成するには, バネ定数や熱伝達係数などの “剛性” に高い値を割り当てます. 数学的に言えば, これは実際にはディリクレ条件の ペナルティ 実装です. 剛性が高いほど, 自由度の規定値の精度が高くなります. ただし, 注意点があります. 剛性が非常に高いと, 剛性行列の数値的条件付けが損なわれます. 熱伝達の問題の場合, “高い” 熱伝達係数 \alpha を選択するための出発点は, 次のようになります
ここで, \lambda は熱伝導率, h は特性要素サイズです.
同じ考え方は, \lambda を適切な材料特性 (固体力学のヤング率など) に置き換えることで, 他の物理分野にも適用できます. 係数 1000 は単なる提案であり, 104 または 105 に置き換えることができます.
前の例の 450 K の移動するスポットを対流を使用してモデル化する場合は, 以下に示す設定を使用できます. 要素サイズの組み込み変数 h が式に適用されます.
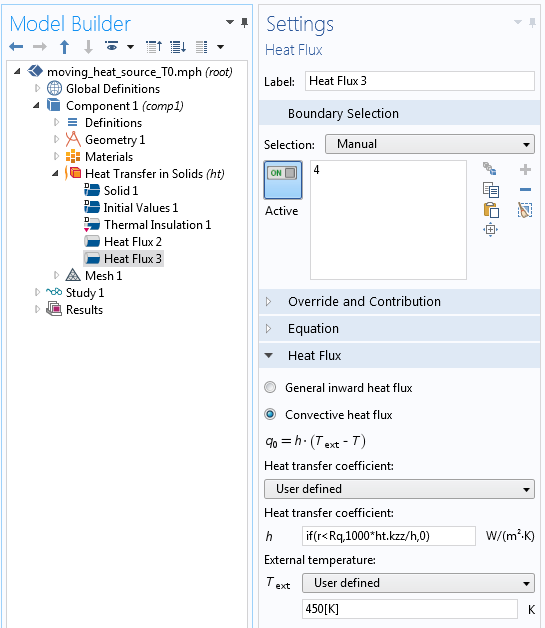
対流条件を使用して温度を指定します.
古き良き時代, 私が初めて有限要素解析を使い始めた頃は, 構造力学の有限要素プログラムで非ゼロ変位を指定できないことがありました. プログラミングの複雑さが増したために制限されていました. その場合, 最適な選択肢は, 事前に変形した硬いバネを追加してペナルティ法を使用することでした. ただし, 硬すぎるのは望ましくありません. 当時はまだ単精度演算が使用されていました.
ノイマン条件の近似に注目してみましょう. 表面温度に依存しない熱流束が必要です. 熱伝達の場合, ロビン条件は, 内向きの熱流束 q が
ここで, \alpha は熱伝達係数, T は境界の温度, T_{\textrm{ext}} は外部温度です.
したがって, T_{\textrm{ext}} が表面の予想温度よりもはるかに大きい場合, q \approx \alpha T_{\textrm{ext}} となります. その場合の方法は, 任意の非常に大きな T_{\textrm{ext}} を選択し, 以下で強調表示されているように, 適切な熱伝達係数を計算することです.
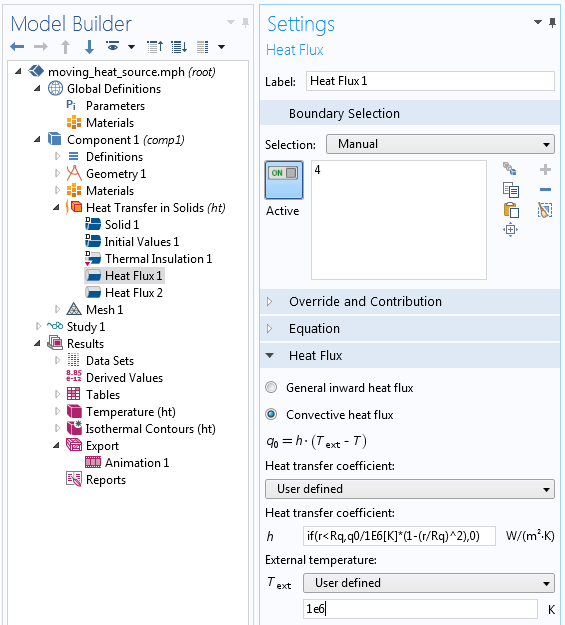
対流条件を使用して熱流束を規定します.
設計者は実際にこの原理を使用して, 実際の機械部品に固定の力を導入します. つまり, プレストレスを与えられた長くて弱いバネです. バネのプレ変形がバネが接続されている部品の変位よりもはるかに大きい場合, バネの力はほぼ一定になります.
離散化エラーへの対処
境界条件が if(r < R,... のようなブール式によって拘束されている場合, その条件が適用される領域の境界がメッシュ要素のエッジに沿わない可能性が高くなります. これにより, 離散化エラーが発生します.
ノイマン条件またはロビン条件の場合, 数値積分は各有限要素に対して実行されます. 関数の値は, 要素内のいくつかの 離散ガウス点 で評価されます. メッシュ要素のサイズが負荷の幾何学的サイズに比べて大きい場合, 負荷によってカバーされるガウス点の正確な数が総負荷に大きな影響を与える可能性があります. そのため, どの瞬間にも, 負荷によってカバーされるパッチ上に複数の要素が存在する必要があります.
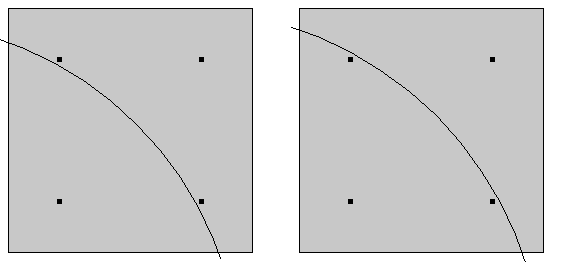
荷重位置の小さな変更により, 寄与積分ポイント数が変わる場合があります. (実際には, 積分ポイントの数はより多くなります.)
代わりに, 少なくとも点ごとの意味でのディリクレ条件がメッシュノードに適用されます. 下の図では, 指定された温度 450 K で移動する円形スポットをシミュレーションする際の一定時間の温度分布と熱流束が示されています. ホットスポットの前には, 260 K の暗い色合いが見えます. シミュレーションの初期温度と周囲温度は 293 K なので, これは予想外です. これは, 各要素のすべてのノードにディリクレ条件があるわけではないという事実に関連する数値アーティファクトです. ディリクレ条件の不連続点では, 特異点が発生します. これは, 以前のブログ で議論されているトピックです. メッシュを改良すると, このような影響が軽減されます.
次の図の緑の矢印は, 温度の指定に対する反応として熱の流入が生成されるノードを表しています. モデルのメッシュ密度では, 半円の近似はかなり粗くなります.
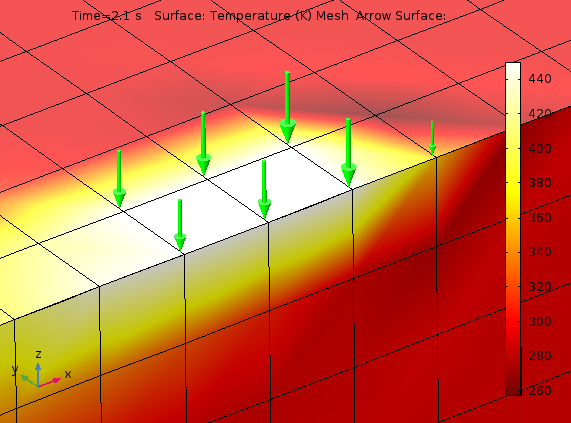
半円状の規定温度周辺の温度分布と熱流束.
境界条件における解の依存性
解が境界条件に入る方法は多数あります. 通常, これによって非線形性が生じますが, これは COMSOL Multiphysics によって自動的に検出されます.
例として, 梁の少し下に配置された支持を備え, 一定のたわみの後にそれ以上の動きを阻止する梁を見てみましょう. これは, 梁 インターフェースの 指定された変位/回転 ノードを介して条件付きディリクレ条件で実装できます.

たわみのある梁, 支持と分散荷重の制御.
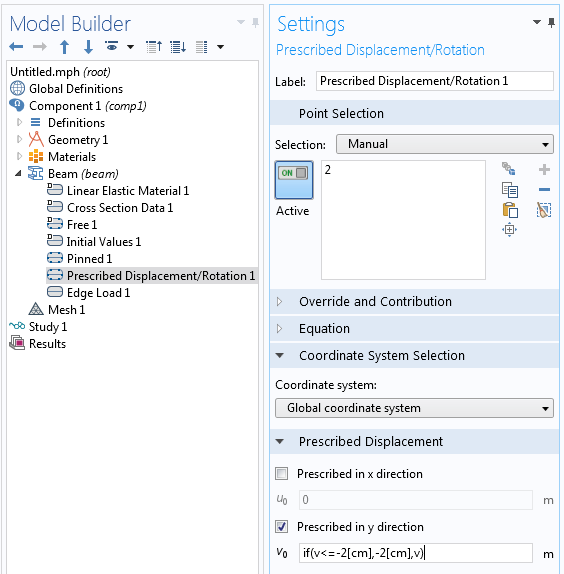
梁が 2 cm のたわみで停止するように指定する設定.
解析では, 予想どおりの動作が示されています. 低荷重ではたわみの形状は対称ですが, 高荷重レベルでは, 梁上の追加支持が配置されているポイントの動きが停止します. 最終荷重レベルでは, 梁の曲率の符号が変わります. これは変形プロットで確認できますが, 曲げモーメントグラフではより明確に表示されます.
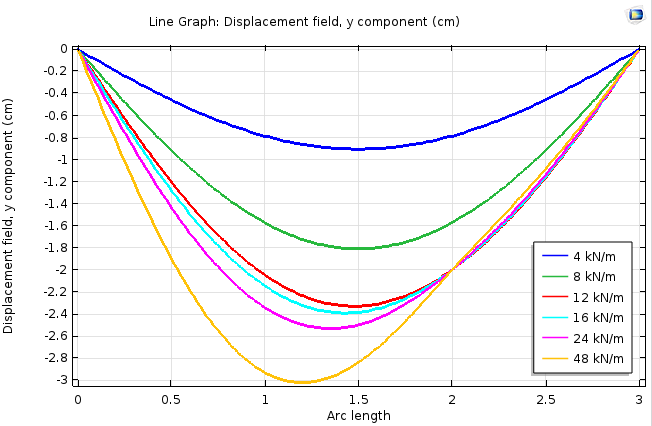
支持点の梁の変位は 2 cm で停止します.
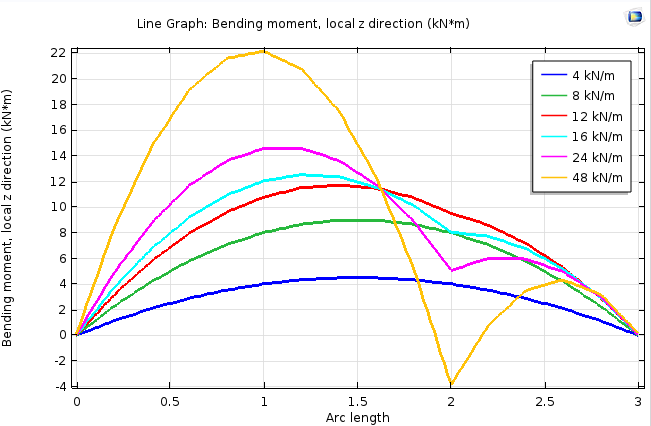
さまざまな荷重レベルにおける梁に沿った曲げモーメント.
ここで強調されているアプローチはかなり粗雑で, 反復解は良好な収束特性を持たない可能性があります. より安定した実装は, 支持点で高度に非線形なスプリングを使用することです. これにより, 反力は変位の連続微分可能な関数になります. これは, 実際には, 固体力学 インターフェースでペナルティ接触が実装される方法に似ています.
COMSOL Multiphysics での境界条件の利用に関する結論
COMSOL Multiphysics では, 非標準の境界条件を規定するための非常に強力なメカニズムにアクセスできます. 今日は, これらの条件を使用して何ができるかについて, いくつかの例を示しました.
移動荷重のあるモデルの解析に関心のある方は, アプリケーションギャラリで入手可能な 移動荷重チュートリアルモデル をご覧ください.
独自のモデリングプロセス内で非標準境界条件を規定する方法についてさらに質問がある場合は, 今すぐ お問い合わせ ください.





コメント (0)