
COMSOL Multiphysics® ソフトウェアの強みの1つは, 時間の経過とともに変化する荷重と制約を簡単に定義できることです. 実際には, ソフトウェアのコア機能内でこれを行う方法はいくつかあります. 今日のブログでは, これらのアプローチのうち3つについて説明します.
例: 平板のレーザー加熱
レーザー熱源によって加熱されている平らな板状の材料の場合を考えてみましょう. 下の図に示すように, 板の中心は原点にあり, 時間の経過とともに表面のさまざまな場所を加熱したいと考えています. レーザー (またはワークピース) は, 焦点の位置を制御できるステージに取り付けられているとします. また, レーザーのビームプロファイルを形成する光学系があり, 熱源が焦点の周りの小さな領域に広がっていると仮定します.
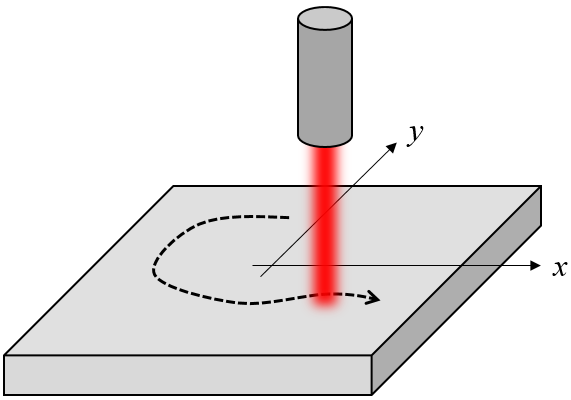
ワークピース上を移動するレーザー熱源の概略図.
ここで, 既知のツールパスに沿って移動する焦点ポイントを定義するさまざまな方法を見てみましょう.
方法1: 変数を使う
最もシンプルなアプローチは, 一連の変数を使用して, 焦点の位置と熱負荷の分布を時間とともに定義することです. たとえば, 10秒ごとに半径 40 cm の円形の経路で移動する合計 1 kW の熱負荷があるとします. さらに, 熱負荷は 5 cm のビームウエスト半径を持つガウス強度分布を持ちます. この情報は, 以下のスクリーンショットに示すように, 変数を使用して定義できます.
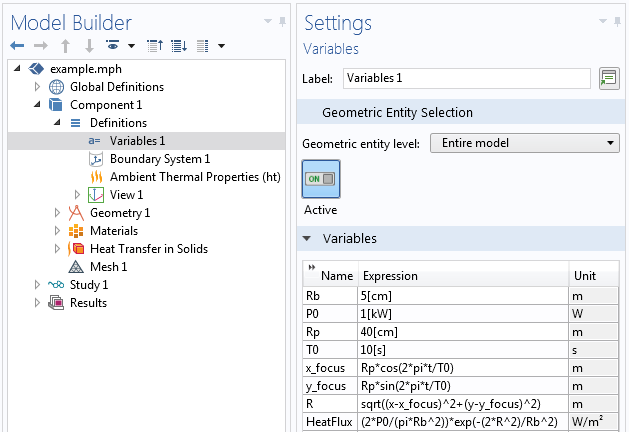
最初の4つの定義, Rb, P0, Rp, T0 は, 実際には単なる定数です. 後でパラメトリックスイープを使用してこれらの定義のいずれかを変更する場合は, それらをグローバルパラメーターとして定義することもできます. 現時点では, すべてを1か所に表示するのが最も簡単です.
次の2つの変数, x_focus と y_focus は定数ではありません. これらは時間の関数, つまり組み込み変数 t に応じて変化します. これらの変数は, 原点を中心に円軌道上を移動する点を表していることがわかります:
Rp*cos(2*pi*t/T0)
Rp*sin(2*pi*t/T0)
次の変数 R は, 時間と空間の関数です. これは, 座標変数 x と y, および先ほど説明した時間の関数である x_focus と y_focus を使用します. したがって, 時間の各瞬間と空間の各ポイントで, この変数はレーザー焦点からの距離 (xy 平面内) を示します.
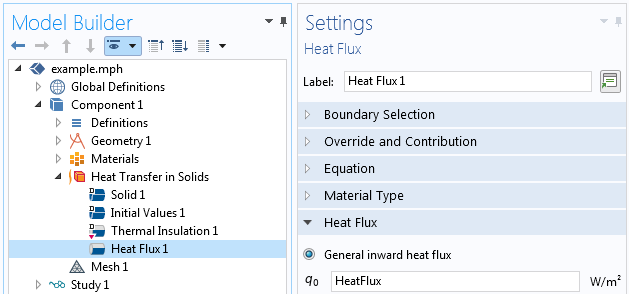
最後の変数 HeatFlux は, R と定数の関数です. これは, 合計熱流束が定義された電力と等しくなるように, 焦点の周りのガウス強度プロファイルを定義します. 下のスクリーンショットに示すように, 境界条件として入力するのはこの変数 HeatFlux です.
この規定された熱流束式により, 以下に示すような加熱プロファイルパスが与えられます.
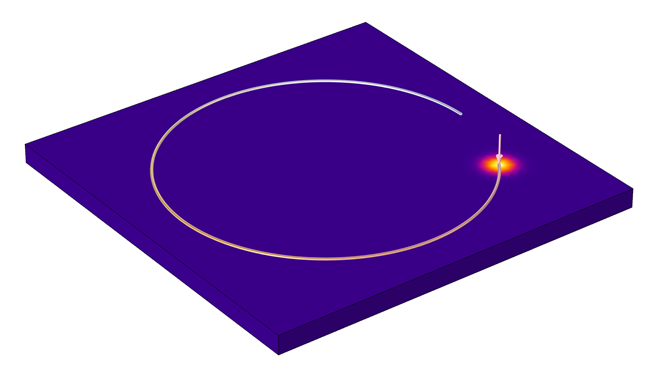
変数ノードで設定された円形加熱プロファイル.
方法2: 補間関数を使う
ここまでは, それほど複雑ではありません. 数式があるだけです. しかし, x_focus と y_focus の簡単な式を, もっと一般的なものに置き換えることができます. COMSOL Multiphysics は, ソフトウェアにさまざまな組み込み関数を提供しています. ここでの説明で最も便利なのは, テキストファイルからデータを読み込むことができる補間関数です. 時間のデータ行とその時点のレーザー焦点の x 位置と y 位置を含むテキストファイルがあるとします. このようなファイルのサンプルを以下に示します:
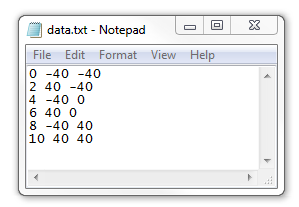
このようなデータは, 以下に示す設定を使用して, 補間関数に読み込むことができます. ここでは, 引数は1つだけ (時間) であり, その後の2つのデータ列は, それぞれ x 焦点と y 焦点をセンチメートル単位で表していることに注意してください. 指定された時間点の間では, レーザーが直線的に移動するようにします. 関数名をそれぞれ x_f と y_f として指定し, 引数を正しく設定してください.
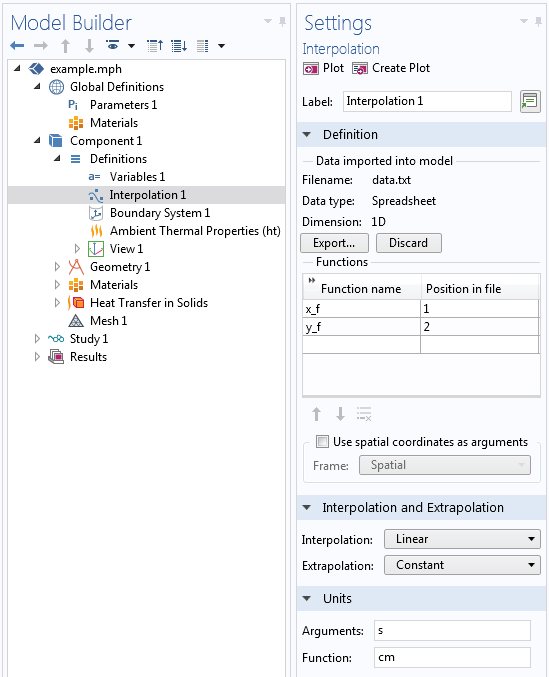
次に, 焦点の前の式を x_focus = x_f(t) および y_focus = y_f(t) に変更するだけで, 下図のような移動荷重が得られます.
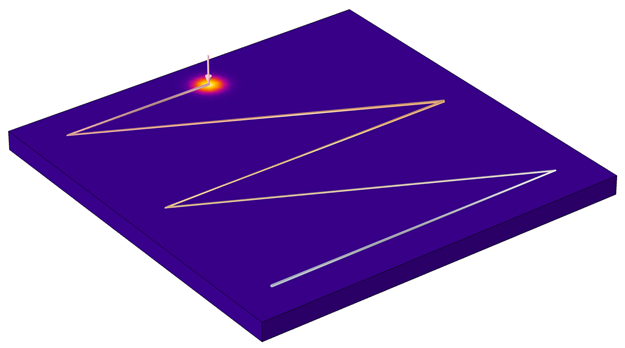
テキストファイルから読み込まれた加熱プロファイル.
この補間関数を使用すると, 非常に複雑なプロファイルパターンをすばやく読み込めることがわかります. 必要なのは, これらのプロファイルとテキストファイルを生成する方法だけです. たとえば, ここで使用されているテキストファイル形式は G コード 形式とそれほど変わらないため, このような形式で加熱パスを定義している場合は, それを COMSOL® 対応の入力に変換するのは非常に簡単です. 一方, 一般的な 2D DXF ファイル形式で作成されたプロファイルをインポートしたい場合もあります. 次にそれを見てみましょう…
方法3: CAD ジオメトリからインポートされた経路を使う
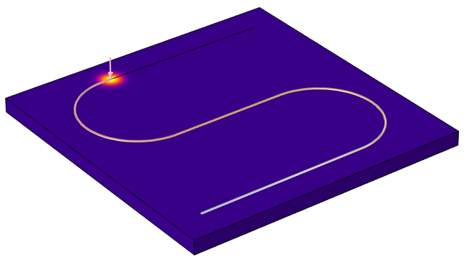
下の画像に示すように, 外部ファイルから読み込んだパスに沿って荷物を移動させたいとします. レーザーがこのパスに沿って端から端までスムーズに移動するようにします. ここで, もう少し作業が必要です.
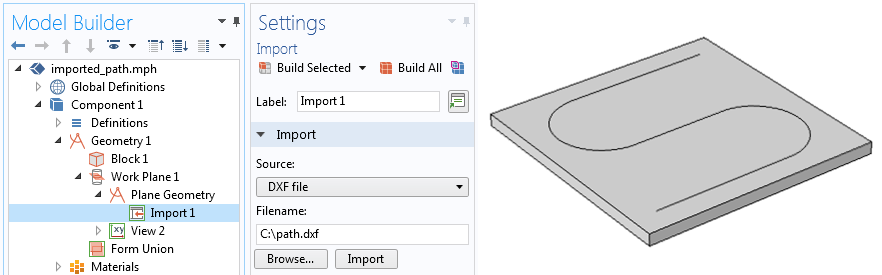
レーザーパスの S 字型プロファイルは, DXF ファイルからジオメトリとして読み込まれます.
読み込んだファイルには時間に関する情報は含まれていません. これは, レーザーが一定速度で進むと予想されるパスにすぎません. インポートしたパスの各エッジ (エッジは数千ある可能性があります) には, 長さに沿って線形に変化するパラメーター s1 と s2 がありますが, エッジが多数ある場合は, これらのパラメーターを操作したくないでしょう. では, 代わりに, すべての線に沿って, すべての時点でレーザーがどこにあるかを計算するにはどうすればよいでしょうか. これを行う1つの方法は, 別の偏微分方程式 (PDE) を導入して, 目的の線に沿って解くことです. 解きたい PDE は次のとおりです:
ここで \nabla_t は曲線の接線方向を示します.
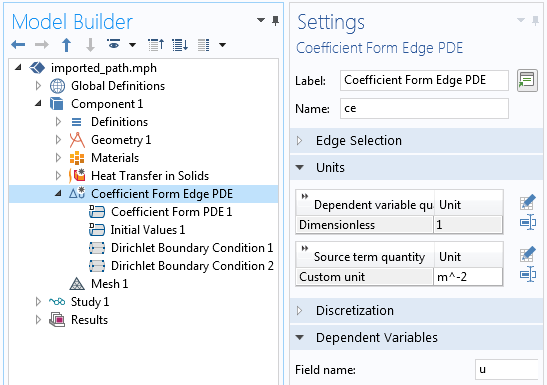
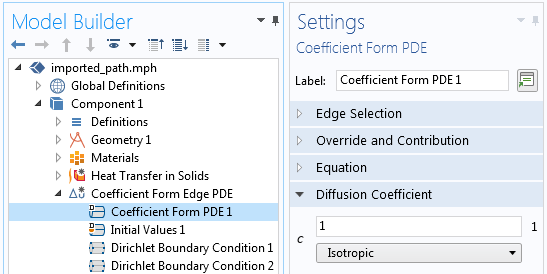
この PDE は, パスの一方の端で u = 0, もう一方の端で u = 1 という境界条件とともに, パスに沿って0から1まで線形に変化する場を提供します. この場は, すべてのエッジの合計弧長に比例します. これは, 以下のスクリーンショットに示すように, 係数形式エッジ PDE インターフェースを使用して設定できます. 拡散係数, c 以外のすべての係数項は, ゼロに設定されています.
左: パスを計算するために必要な係数形式エッジ PDE インターフェースの設定. 右: 拡散係数項 c は定数です. 他のすべての係数はゼロに設定されています.
次に, 2つのディリクレ境界条件によって, 場 u が両端に設定され, 熱伝達問題を解く前に, 同じスタディ内でこの PDE を定常ステップで解きます.
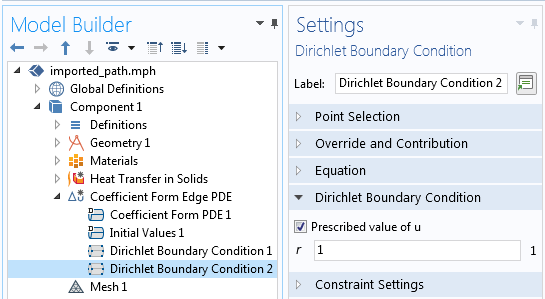
プロファイルパスの開始と終了で, 場を制約するために2つのディリクレ境界条件が使用されます.
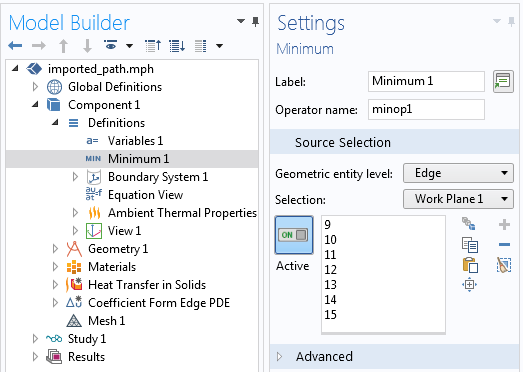
次に, ソースをたどるエッジとして選択した単一の最小演算子をモデルに導入します. この最小演算子は, 焦点座標を定義するために使用されます. 例えば:
x_focus = minop1(abs(u-t/T0),x)
y_focus = minop1(abs(u-t/T0),y)
最小演算子には2つの引数が与えられることに注意してください. 2つの引数で演算子を呼び出すと, 最初の引数が最小値である2番目の引数の値が返されます. したがって, 各時間 t で, 端から端までの t/T0 分数にあるエッジ上の点の x 位置と y 位置が返されます.
左: 最小演算子は, 熱源がたどるパス上で定義されます. 右: インポートされた DXF ファイルによって定義されたパスをたどるレーザー熱源.
では, レーザーがパスのさまざまな部分をさまざまな速度で通過するようにしたい場合はどうでしょうか. それらのエッジセットに沿って係数 c を調整するだけで済みます. レーザーが曲線の境界に沿って直線に沿った場合よりも3倍速く移動するようにするには, c を3倍大きくするだけです. 絶対値は重要ではなく, 係数の大きさの比率が重要であることに注意してください. このアプローチの唯一の欠点は, パスが交差するときに発生します. その場合, パスを2つ以上のパスグループに分割し, それぞれで PDE を解き, 変数の記録をもう少し行う必要があります.
おわりに
このブログでは, 移動荷重をモデル化する3つの異なるアプローチについて説明しました. 実際に試してみるには, 下のボタンをクリックしてアプリケーションギャラリに移動してください. そこで, 上記のモデルの MPH ファイルをダウンロードできます.
アプリケーションギャラリ内の他のいくつかの例でもこれらの技術が使用されています:
このブログでは荷重のみを考慮しましたが, シミュレーションで境界条件を条件付きにする方法で説明されているように, これらの手法を制約に適用することもできます.
モデリングアプリケーションでの COMSOL Multiphysics の使用についてさらに質問がありませんか? ぜひお知らせください.






コメント (0)