The KdV Equation and Solitons
Application ID: 85
The Korteweg-de Vries (KdV) equation models water waves. It contrasts sharply to the Burgers equation, because it introduces no dissipation and the waves travel seemingly forever. Solitons have their primary practical application in optical fibers. Specifically, a fiber’s linear dispersion properties level out a wave while the nonlinear properties give a focusing effect. The result is a very stable, long-lived pulse. This solution says that the pulse’s speed determines its amplitude and width. This simulation illustrates this effect.
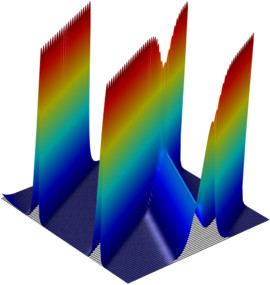
この model の例は, 通常次の製品を使用して構築されるこのタイプのアプリケーションを示しています.
ただし, これを完全に定義およびモデル化するには, 追加の製品が必要になる場合があります. さらに, この例は, 次の製品の組み合わせのコンポーネントを使用して定義およびモデル化することもできます.
アプリケーションのモデリングに必要な COMSOL® 製品の組み合わせは, 境界条件, 材料特性, フィジックスインターフェース, パーツライブラリなど, いくつかの要因によって異なります. 特定の機能が複数の製品に共通している場合もあります. お客様のモデリングニーズに適した製品の組み合わせを決定するために, 製品仕様一覧 を確認し, 無償のトライアルライセンスをご利用ください. COMSOL セールスおよびサポートチームでは, この件に関するご質問にお答えしています.



