アプリケーションギャラリ

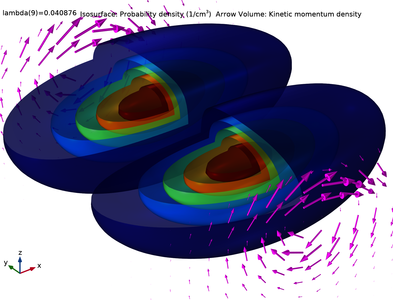
This tutorial model solves a two-component Schrödinger equation for the eigenstates of a simple silicon quantum dot in a uniform magnetic field, based on the paper by Jock et al. on the topic of spin-orbit qubits. The built-in domain condition Lorentz Force for the Schrödinger Equation interface is used to account for the contribution to the kinetic momentum from the vector potential. The coupling of the spin-up and spin-down components is implemented using the built-in domain condition Zeroth Order Hamiltonian. Together with the benchmark model k dot p Method for Strained Wurtzite GaN Band Structure, these examples show how to set up multiple wave-function components with the Schrödinger Equation interface. The computed probability density and kinetic momentum density of the ground state compare well with Supplementary Figure 1 in the paper. In addition, the computed energy difference between the first two eigenstates agrees well with the expected value from an intuitive analytic calculation.