Problem Description
I am solving a transient model and am expecting the solution to oscillate over time in response to step changes in the loads. How should I set up such a model? What solver changes should I make?
Solution
Certain models will produce solutions that are wave-type, or oscillatory in time in response to time-varying loads. Common examples include the transient pressure acoustics formulation and the transient electromagnetic wave formulation. The governing equations are hyperbolic partial differential equations, the solutions to these represent sound waves and electromagnetic waves, respectively. The Structural Mechanics interfaces in the time-domain can also produce oscillatory solutions. For example, consider the problem of a tensioned guitar wire: When the wire is abruptly plucked, it will vibrate at its fundamental frequency, as well as at a number of higher overtones.
Regardless of the physics being solved, all such models require a bit of care in how the loads are applied, because of the way in which the COMSOL time-dependent solver chooses the time-step to compute the solution. By default, the software automatically adjusts the timestep size to capture (within the specified tolerance) the response of the system. This can lead to a very small timestep if the applied load is instantaneously changing in time.
Consider, for example, a load that varies in time (as shown below) along with its Fourier Transform. The load changes instantaneously and this leads to a lot of high-frequency content. Although the magnitudes of these higher-frequency components does drop off, they can still be significant. If we excite a structure with such a load, the software would try to resolve all of this high-frequency content, and it would start taking very small timesteps (proportional to a fraction of the period) to compute the system response.
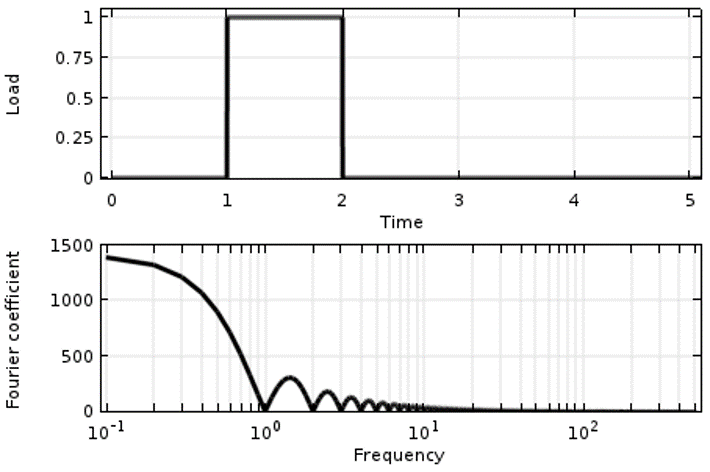
A Step Load in time and its Fourier transform
From a modeling point of view, though, we may not actually be interested in all of this high-frequency content (the higher overtones, small vibrations, etc... in the solution) The resolution is to smooth the input signal such as to avoid any abrupt changes. This is physically motivated, since most loads cannot truly change instantaneously in time. It is also reasonable from a modeling point of view: The high frequency content contains a relatively small fraction of the total energy of the system, and is likely of little practical interest. An example of such a smoothed input signal, as well as its Fourier transform, is shown in red in the image below. Note that the low frequency content of the signal is almost unchanged, but the smoothed signal has negligible higher frequency content past the a certain point, as compared to the original signal.
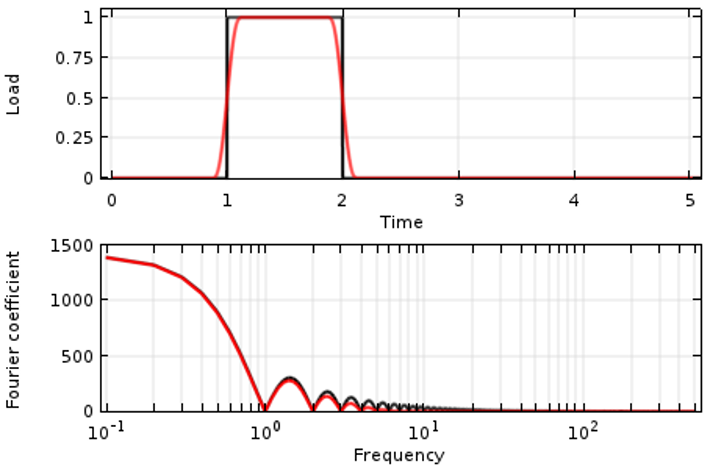
A Smoothed Step Load in time (red curve) and its Fourier transform
The built-in Rectangle, Triangle, Step, Ramp and Waveform of Type Sawtooth, Square and Triangle all include the option to smooth the signal, as shown in the figure below. The Piecewise function also permits smoothing between intervals. If you are setting up other types of user-defined loads, make sure to add some kind of smoothing to them as well. For more information see the COMSOL Multiphysics Reference Manual > Global and Local Definitions > Functions > Specifying Discontinuous Functions > Additional Smoothed Functions.
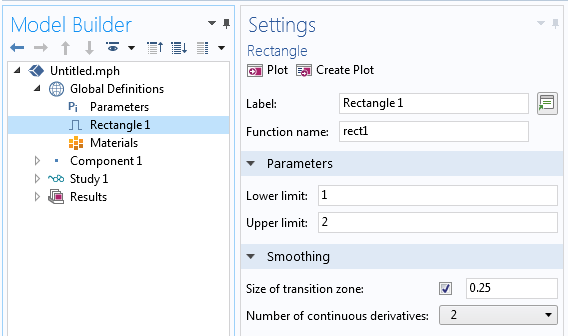
Smoothing of a Built-In Function
Once you have appropriately smoothed all of your loading functions, you will also know the maximum possible frequency content of your excitation. This will let you choose the appropriate mesh, and you can then manually adjust the timestep, as described in: Knowledge Base 1118: Resolving time-dependent waves
See also:
Knowledge Base 1240: Manually Setting the Scaling of Variables
Knowledge Base 1245: Solving Models with Pulsed Loads in Time
COMSOL は, 本ページに掲載されている情報の確認に合理的な努力を払っております. リソースおよびドキュメントは情報提供のみを目的としており, COMSOL はその有効性について明示的または黙示的な保証を行いません. 開示されたデータの正確性について, COMSOL は法的責任を負いません. 本文書で言及されている商標はすべて, それぞれの所有者に帰属します. 商標に関する詳細は, 製品マニュアルをご参照ください.



