
燃料電池は, クリーンエネルギー分野で最も話題になっている新技術の 1 つです. 燃料電池は, 水素と酸素を含む電気化学反応によって電気を生成し, その合計反応により水素の酸化と酸素の還元が生じます. 簡単に言うと, 燃料電池に水素と酸素が安定して供給されれば, 電気が発生します. さらに, この過程で生成される副生成物は水であるため, 二酸化炭素や有害な副生成物を発生しないクリーン燃料です.
異なる燃料電池デザインを試す
燃料電池が最適に機能するには, 電池内の電流密度分布, 反応物質の供給, および温度プロファイルの間のバランスを維持する必要があります. これらの側面は通常, モデリングとシミュレーションを使用して解析されます. マルチフィジックスモデルでは, 熱膨張による構造変形の可能性も考慮できます. COMSOL Multiphysics® ソフトウェアのアドオン製品である 燃料電池&電解槽モジュール を使用すると, 次のことが可能になります. さまざまな燃料電池を設計およびモデル化し, これらすべての側面を単一のモデルに組み込むことができます. このソフトウェアは, 反応流れや非等温流れなどのさまざまなマルチフィジックスカップリングを提供しており, これらを実装することで, 実際のアプリケーションでセルがどのように機能するかを明確に把握できます. これらの解析を燃料電池スタック全体に拡張することもできます.
COMSOL Multiphysics® を使用して燃料電池設計のさまざまな側面を評価する方法の 4 つの例を見てみましょう…
1. 固体酸化物型燃料電池
固体酸化物型燃料電池では, 電解質と電極は金属酸化物(硬質セラミック材料)でできています. このセルの電極は多孔質ガス拡散電極 (GDE) であり, それらの間に固体電解質が含まれてサンドイッチ構造を形成しています. このセクションでは, 固体酸化物燃料電池の電流密度分布チュートリアルモデルを使用したモデリングとシミュレーションにより, 固体酸化物型燃料電池の内部動作を調べます.
このチュートリアルは, 向流を備えた平行チャネル固体酸化物型燃料電池の単位セル内の電流密度分布をモデル化します. このセルの燃料は加湿された水素ガス (水素と水蒸気) であり, アノード側から入ります. カソード側には加湿空気(水蒸気, 酸素, 窒素)が供給されます.
図 1. バイポーラープレートを含む, スタック内の 1 つのセルの固体酸化物型燃料電池の形状 (左). モデルのジオメトリは, 1 つの空気流路と 1 つの水素流路を含む 1 つの単位セルです (右). バイポーラープレートは一定の電位であると想定されており, モデルには含まれていません. 代わりに, 電位は GDE とバイポーラープレート間の接触面の境界条件として設定されます.
このモデルは次のフィジックスの完全連成を含みます:
- アノードとカソードの質量バランス
- ガス流路中の流れ
- 多孔質電極中のガス流れ
- 酸化物イオンが運ぶイオン電流のバランス
- 電子電流のバランス
- アノードとカソードでの電荷移動反応(電気化学反応)
真のマルチフィジックス問題であるこのモデルには, 細胞内で発生するプロセスと現象を記述するいくつかのフィジックスインターフェースが含まれます. マックスウェル・ステファンの拡散方程式と対流方程式は, 気相内の物質輸送を記述しており, これらは水素燃料電池インターフェースで求解されます. 開いた流路を通る流れは, 圧縮性ナビエ・ストークス方程式によって定義され, ブリンクマン方程式は多孔質電極内の流速を記述します. 電解質, 細孔電解質, および電極内の電流バランスは, 熱力学に関するネルンスト方程式によるGDE 内の局所濃度, および電荷移動反応速度論 (電極速度論) に関するバトラー・ボルマー式を連成させて, 多孔質電極理論を使用して定義されます.
このモデルで調査する興味深いパラメーターは, 次の関係です:
- 流路幅
- 電極厚み
- 電解質導電率 (多孔質電解質を含む)
- 電極導電率
- セル長さ
- ガスの組成と供給率
これらの設計パラメーターと動作パラメーターによって, さまざまな負荷におけるセルの性能が決まります. モデルは完全にパラメーター化されているため, 上記のパラメーターのさまざまな値に対してシミュレーションを実行して, セルの動作を理解および調べることができます. 以下のセクションでこのモデルの結果のプレビューを参照し, アプリケーションギャラリのMPHファイルとPDFマニュアルをチェックして, そのモデルがどのように構築されているかの詳細を見てみましょう.
モデルの結果
図 2 のプロットは, 左から右に, アノードの水素モル分率, カソードの酸素モル分率, および電解質上の電流密度を示しています. このモデルは, 空気の供給によりセルの性能が制限され, その結果, 空気入口での電流密度が高く, 空気出口での電流密度が低くなることが示されています. さらに, 電流密度は, 電流コレクターとフィーダーの接触面がガスの輸送を妨げている端に比べて, 流路の中央でわずかに高いことがわかります.
図 2. セル電圧 0.6 V におけるアノードでの水素モル分率 (左) とカソードでの酸素モル分率 (中央) を示すプロット. ガス流路とガス拡散電極の組成が示されています. 電解質内の電流密度分布 (右) は, 空気の供給によってセルの性能が制限され, 空気入口の位置で高い電流密度が発生することを示しています.
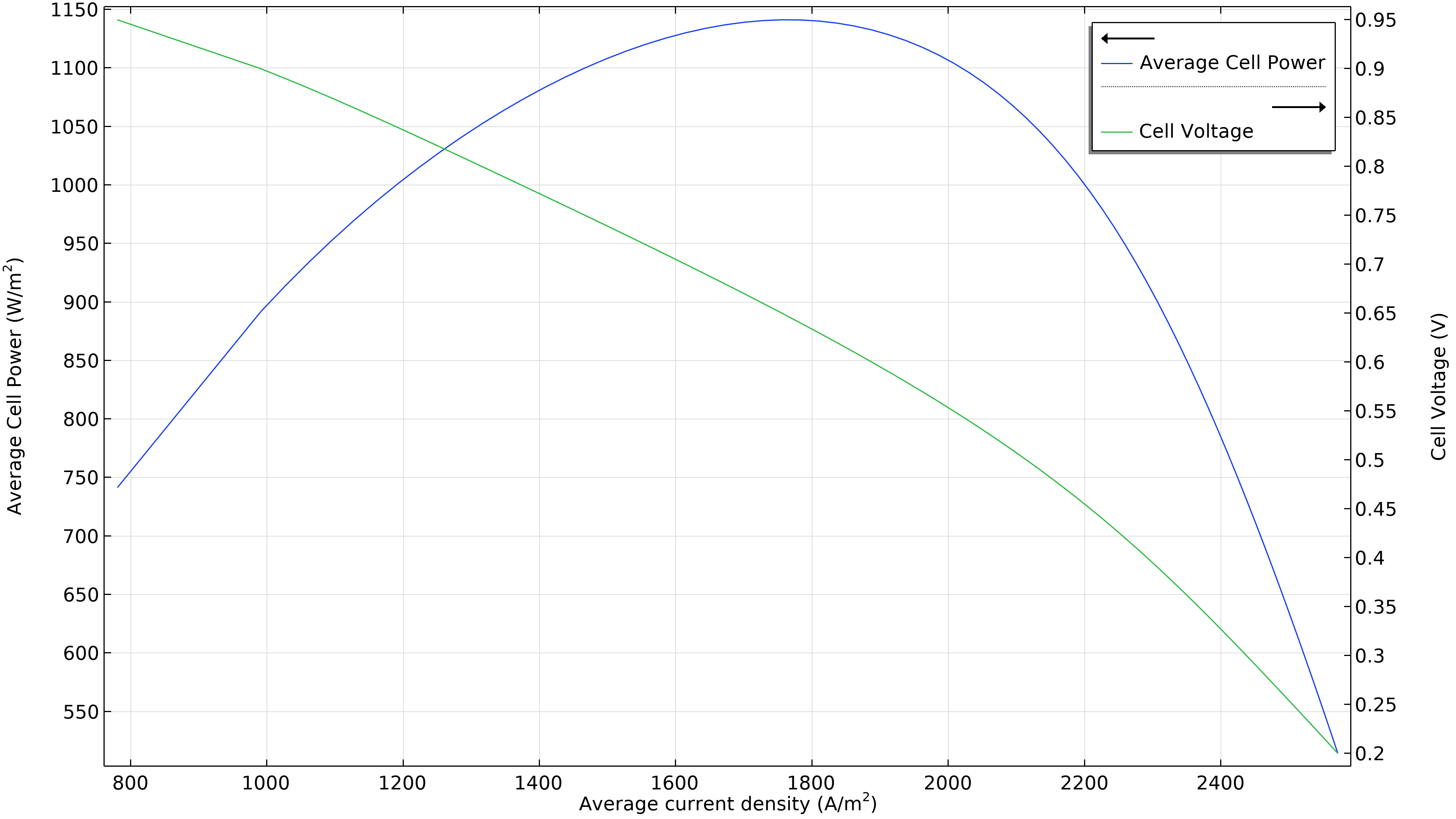
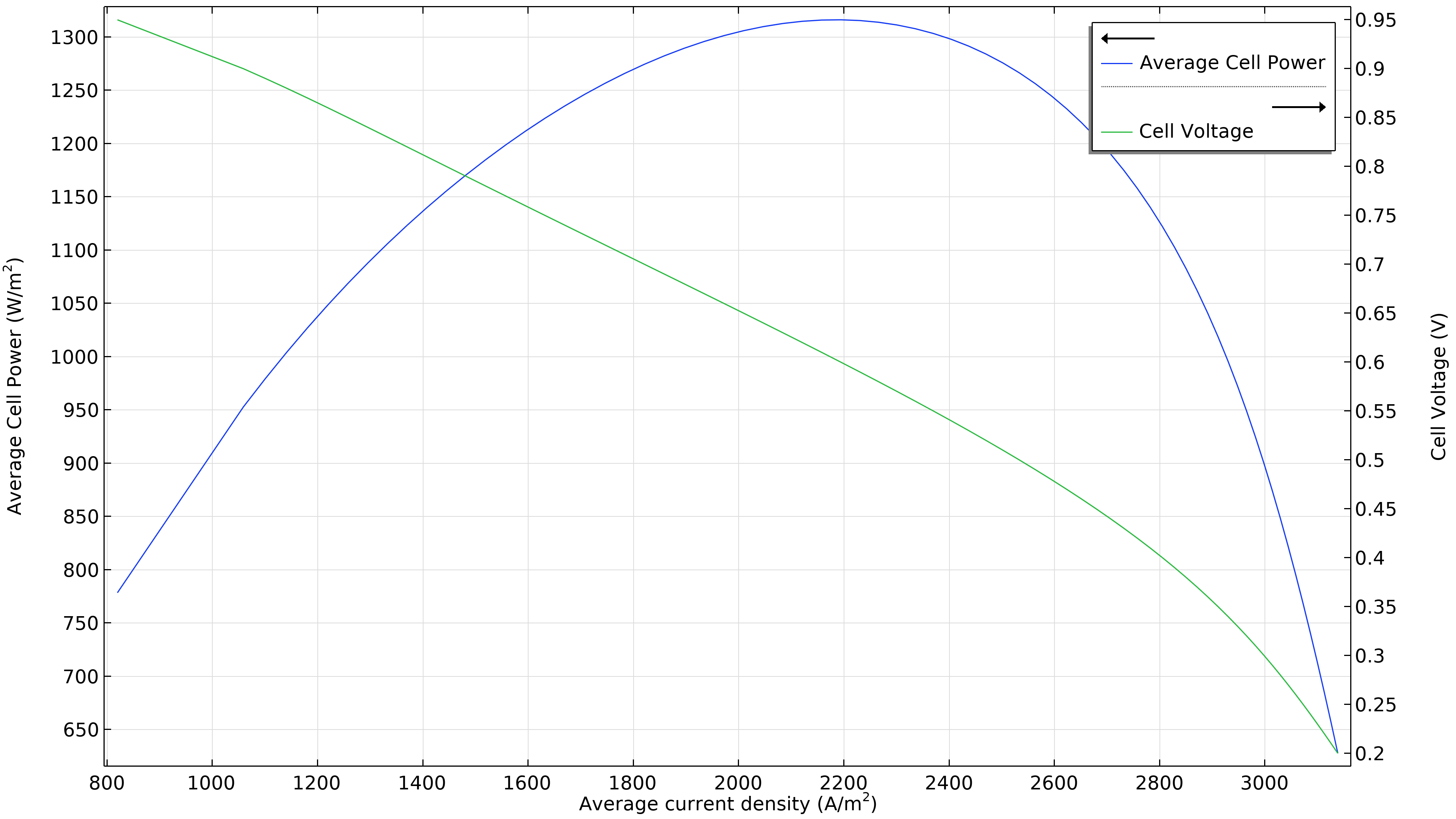
図 3 は, 図 2 の動作条件での最大電力が 1800 A/m2 未満の電流密度であることを示しており (下の左のプロット), 最大電力は 1150 W/m2 未満になります. 空気流量が増加すると, 最大電力密度は 1300 W/m2 まで増加します (下の右のプロット). 電解質内の電流密度分布をプロットすると, それが大幅に均一になっていることがわかります. ただし, このパフォーマンスの向上は, 50% 高い圧力を供給する必要があるエアーポンプに必要な出力とのバランスを取る必要があります.
図 3. 空気流入圧力 6 bar での分極と出力密度の曲線 (左). 約 1800 A/m2 で最大出力が 1150 W/m2 をわずかに下回っていることを示しています. 流入圧力を 9 bar (右) に上げて空気流量を増やすと, 最大値がより高い電流密度 (2200 A/m2) とより高い電力密度 (1300 W/m2) にシフトします .
2. 低温 PEM 燃料電池
プロトン交換膜 (PEM) 燃料電池は, 電解質としてポリマーメンブレインを備えています. 一般に, PEM は動作中に比較的高い含水量を持ちます. 蛇行流場を備えた低温 PEM 燃料電池 チュートリアルモデルでは, メンブレイン電極アセンブリ (MEA) とガス拡散電極 (GDE) で構成されます. 蛇行状のガス流路を含むバイポーラープレートの間に挟まれています. 以下の形状では, 入口を備えた空気流路は MEA の上にあり, 入口を備えた水素流路は MEA の下にあります.
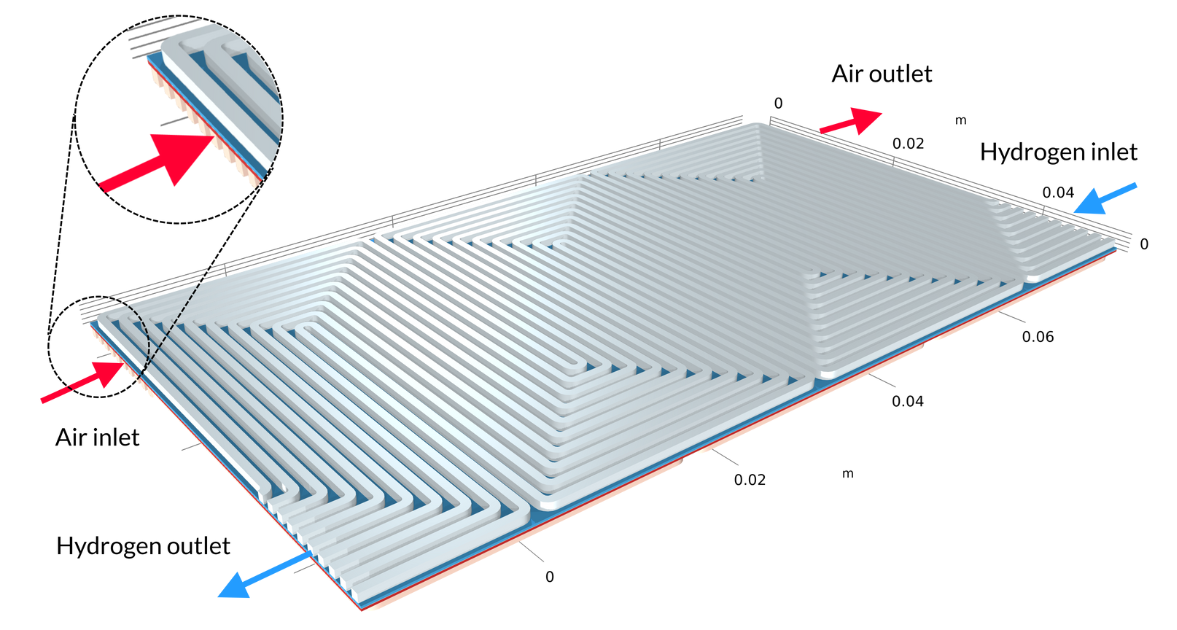
図 4. PEM 燃料電池モデルの形状.
PEM 燃料電池は, アノード (負極) での水素酸化反応とカソード (正極) での酸素還元反応により, カソードで水を生成します. 生成された水はメンブレインを通ってアノード側に浸透する可能性があります. 水が生成されるカソード GDE から効率的に水が除去されないと仮定します. その場合, 電極細孔の浸水が発生し, 酸素の供給が遮断され, その結果として性能が大幅に低下します. 対照的に, メンブレインと細孔電解質が乾燥しすぎると, 電解質のオーム伝導率が低くなります. したがって, PEM 燃料電池の動作における重要な要素の 1 つは水の管理です.
このモデルは以下を求解します:
- ガス拡散電極とメンブレイン電解質における電荷平衡と物質輸送方程式
- メンブレインの両側の気相の流れ方程式
- 拡散 (透過) と移動 (電気浸透抵抗) によるメンブレイン内での水の輸送方程式
- 電極における電荷移動反応方程式(電気化学反応)
このモデルで調査すべき興味深いのは次の点です:
- 蛇行模様の影響
- 流路断面寸法
- バイポーラープレートと電極間の接触面の幅
- MEA寸法
- セルの全部品の材料特性
これらの側面はすべて, さまざまな動作条件 (ガス供給速度と負荷) で解析できます. このモデルは, 特定のガス供給と負荷に応じてセル設計を最適化するために使用することもできます. 以下のセクションで, このモデルのモデリング結果の概要を確認してください. このモデルを構築するための段階的な手順をすぐに知りたい場合は, こちら をダウンロードしてください.
モデル化の結果
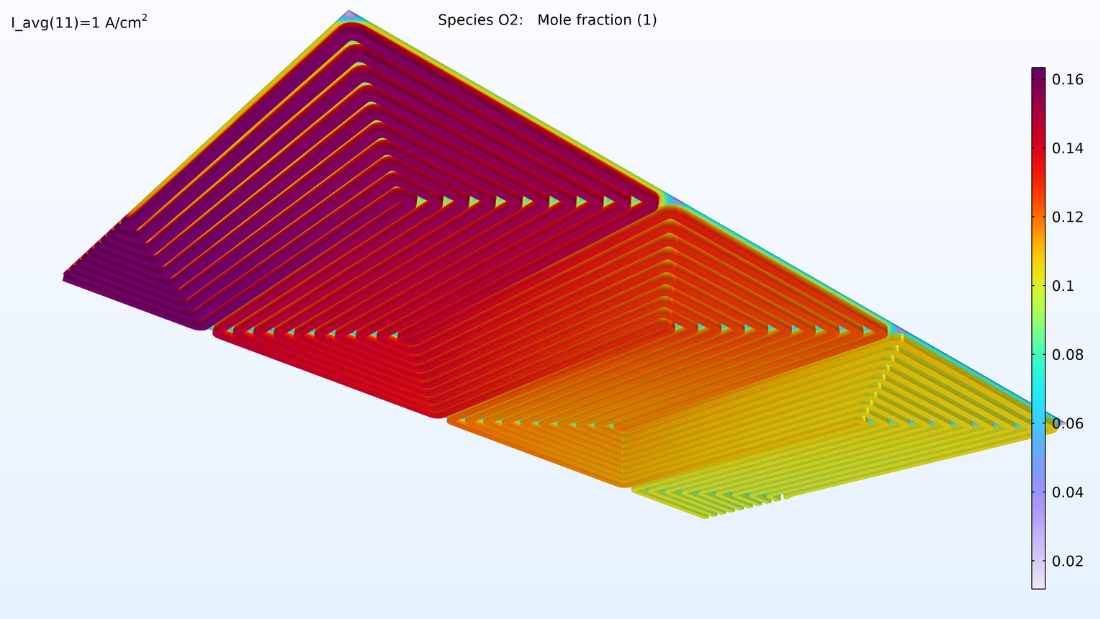
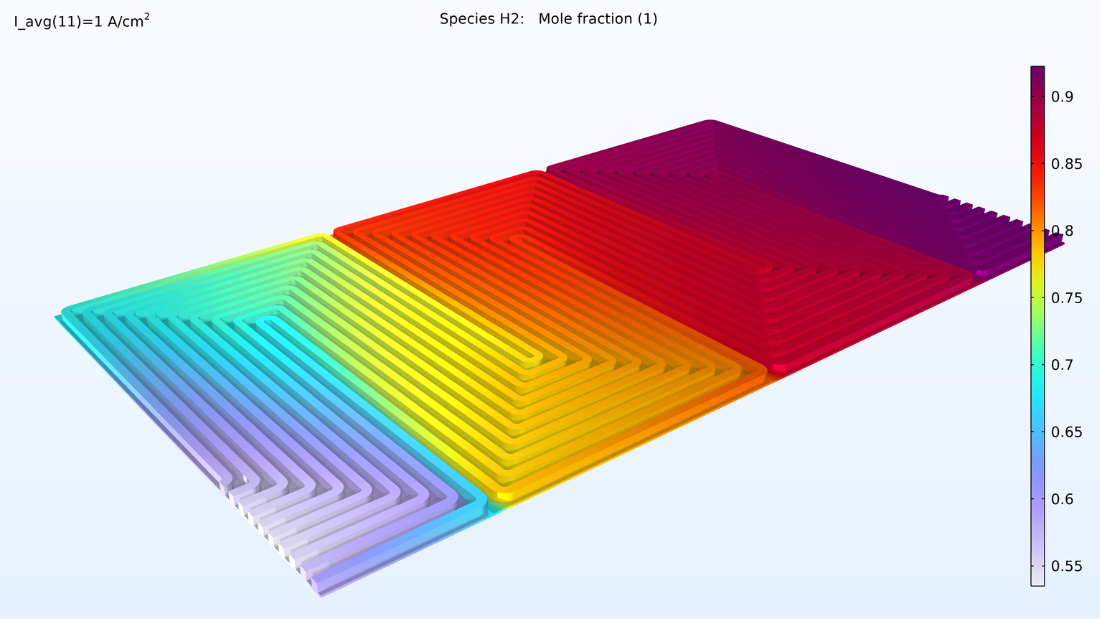
このモデルは, 図 5 のプロットに示すように, それぞれの GDE およびガス流路内のガスの組成を計算します. これらのプロットは, 水素よりも酸素の大幅な減少を示しています. この空乏化は, 主に拡散率が小さい酸素に起因して, GDE の厚さに沿って発生します. 空気と水素の流路の流れは向流であるため, 2 つの反応ガスはバイポーラープレートの両端で枯渇します.
図 5. 酸素モル分率 (左) と水素モル分率 (右) のプロット.
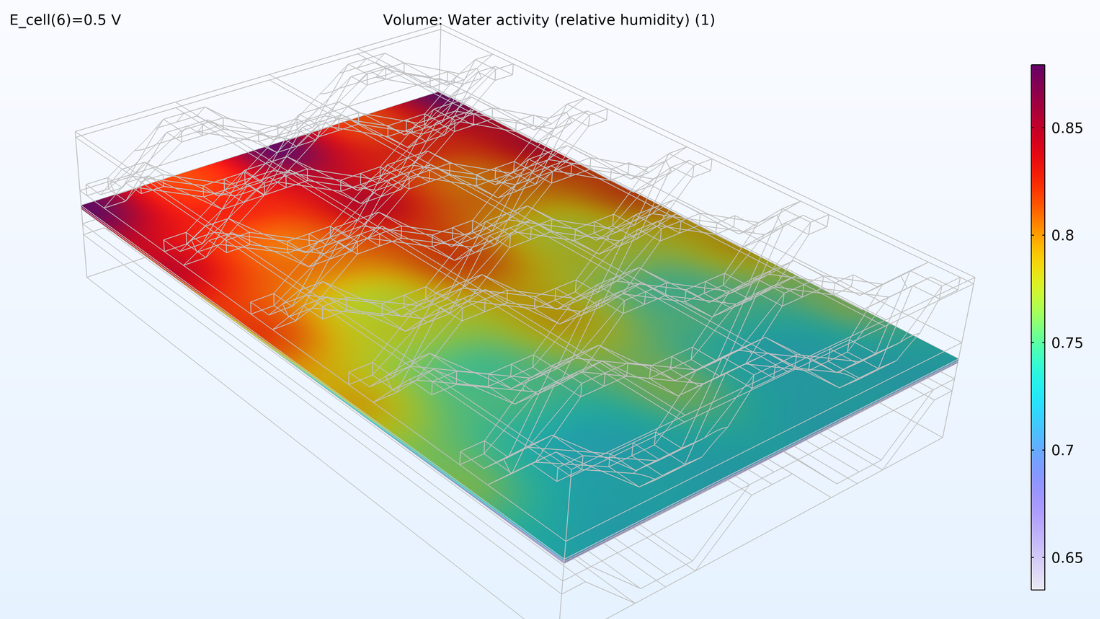
水素流路とメンブレイン内の水分活性を見ると, この活性は空気入口に近いほど大きくなることがわかります. この位置では気相中の酸素含有量が高く, 酸素の輸送により反応速度が制限されるため, 局所電流密度が高くなります. また, 水分活性が大きい位置ではメンブレインの導電率がより顕著になり, セル内のセルの電流密度分布に影響を与えることもわかります. 酸素と水分の含有量により, カソード GDE 内の液体水分がガスの輸送を妨げ始めるまで, 電流密度が増加します.
図 6. 流路内の相対湿度 (左) とメンブレイン内の水分活量 (右) のプロット.
3. 非等温 PEM 燃料電池
非等温 PEM 燃料電池 チュートリアルモデルを使用すると, 相互結合した電気化学反応, 流体の流れ, 熱伝達, 電荷と化学種, PEM燃料電池での輸送をモデル化できます. このチュートリアルのセルには, 電極として機能するガス拡散層 (GDL) の間に挟まれたメンブレイン電解質アセンブリが含まれています. 電極の活性層は表面としてモデル化されており, その幾何学的厚さは無視されています. (活性層の厚さはパラメーターですが, モデルのジオメトリの厚さとしては反映されません. これは, ガス組成と電位が活性層の厚さに沿って一定であることを意味します. ) 水素流路は, 波形プレートによって形成されます. アノードと接触する電流フィーダーとして機能します. 液体の水で満たされた冷却流路が水素流路の反対側を通っています. 空気コンパートメントは, 平らな金属プレートからカソードを分離する拡張メッシュ集電体によって形成されます. 拡張されたメッシュの上に配置された金属プレートは, バイポーラープレートとして機能します. また, カソードコンパートメントを次のセルの冷却流路から分離します. これはスタック内の現在のセルの上に繰り返されることになります.
図 7 の幅は2単位であることに注意してください. 2つの水素流路が含まれています. 幅に沿った対称性により, このジオメトリの 1/4 のみをモデル化する必要があります. ただし, そのような結果は解釈が難しいため, モデルの方程式は数分で解けるので, 必要以上に大きなジオメトリを持つモデルを使用することができます.
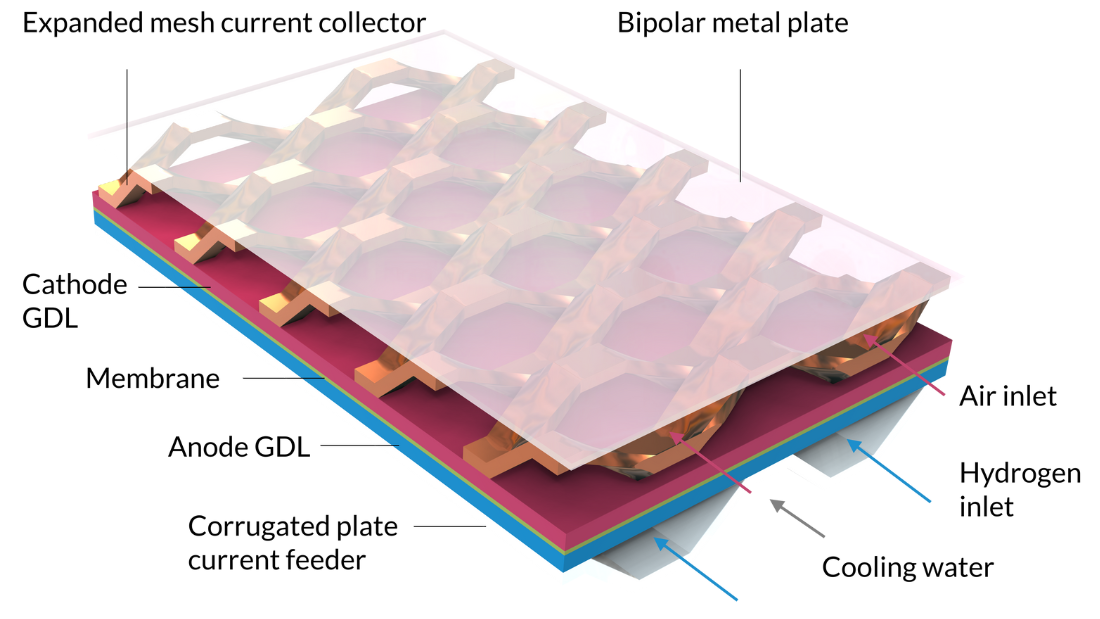
図 7. 非等温 PEM 燃料電池チュートリアルモデルのジオメトリ.
加湿空気と水素ガスの流れ, および液体冷却流体の入口が図の右側に見られます.
冷却液の水は単相流インターフェースを使用した層流のナビエ・ストークス方程式を使用して記述され, セル温度は伝熱インターフェースを使用して定義および求解されます. 細胞の働き全体の理解, 流れ, 化学種輸送, 電気化学反応, セル内の熱伝達などが解析されます. モデル内の次のマルチフィジックスノードを使用して定義されるさまざまなマルチフィジックス現象が含まれます: 反応流, 電気化学加熱, および非等温流.
ここで空気流路に使用される拡張メッシュ構造の影響を解析するのは興味深いです. この構造の目的は, MEA に対して垂直な流れ場成分を作ることです. これにより, 酸素の供給と水分の除去が可能になります. 燃料電池の性能は, 拡張されたメッシュ形状を制御するパラメーターによって異なる場合があります. このようなパラメーターは, 集電体の電極との接触と, 水の除去を含む物質輸送に利用できる面積との関係に影響を与える可能性があります. このモデルにより, 特定の動作条件と負荷に応じて構造を最適化できます. このモデルの結果の概要を以下に示します. その後, アプリケーションギャラリ から PDF ドキュメントと MPH ファイルをダウンロードして, モデルを自分で構築する方法を学習してください.
モデル化の結果
左の以下のプロットはメンブレインの電解質電流密度を示しており, 電流密度は出口側に向かって増加します. これは, メンブレインの導電率が水の形成により含水量とともに増加するためです. メンブレイン内の水分含有量を見ると, 電流密度が大きい集電体とカソード間の接触領域の下に水が溜まっていることがわかります. これは, 水がカソードに溢れ, 酸素の輸送を妨げた場合, 最終的に問題になる可能性があります. 動作条件を一定に保ちながら, 水素流路を 2 倍の長さにしてセルを延長するとします. その場合, 物質輸送の制限により酸素還元反応が遅くなり, 最終的に流路の長さに沿って電流密度が劇的に減少することがわかります.
図 8. セル電圧 0.5 V におけるメンブレインの貫通電解質電流密度 (左) とメンブレインの相対湿度 (右).
このモデルを使用すると, カソードガス混合物中の酸素モル分率と水蒸気モル分率も観察できます. 酸素レベルは出口に向かって減少し, 水レベルは増加します.
図 9. 酸素モル分率 (左) と水素モル分率 (右) のプロット.
さらに, セル全体と冷却流路の温度プロファイルを確認できます. MEA では最高温度が観察されますが, ジュール加熱と活性化損失によって熱源が見つかる場所であるため, これは当然のことです.

図 10. セル内の温度分布.
セル内の電力損失を図 11 に示します. このプロットは, セル内での発熱の分布を示しています. 最も重要な熱源はメンブレイン内にあることがわかります. これはメンブレインの伝導率が低いためです. さらに, 膨張したメッシュがカソードと接触する位置でかなりの熱が発生していることがわかります. ここで, 電極の導電性は(集電体と比較して)相対的に劣りますが, 電流密度は高くなります.

図 11. MEA, 電流供給装置, および電流コレクター内の熱源の対数プロット.
最後に, 平均電流密度 (単位膜面積あたりの電流) の関数としてセル電圧を示すセルの分極曲線を生成できます. 低電流密度でのセル電圧の大幅な低下は, 主にカソードでの活性化過電圧によるものです. 同時に, わずかに高い電流密度では, 抵抗損失が支配的な線形領域が続きます. 高電流密度では損失がわずかに増加しており, 物質輸送抵抗により曲線がわずかに下向きに曲がっています.
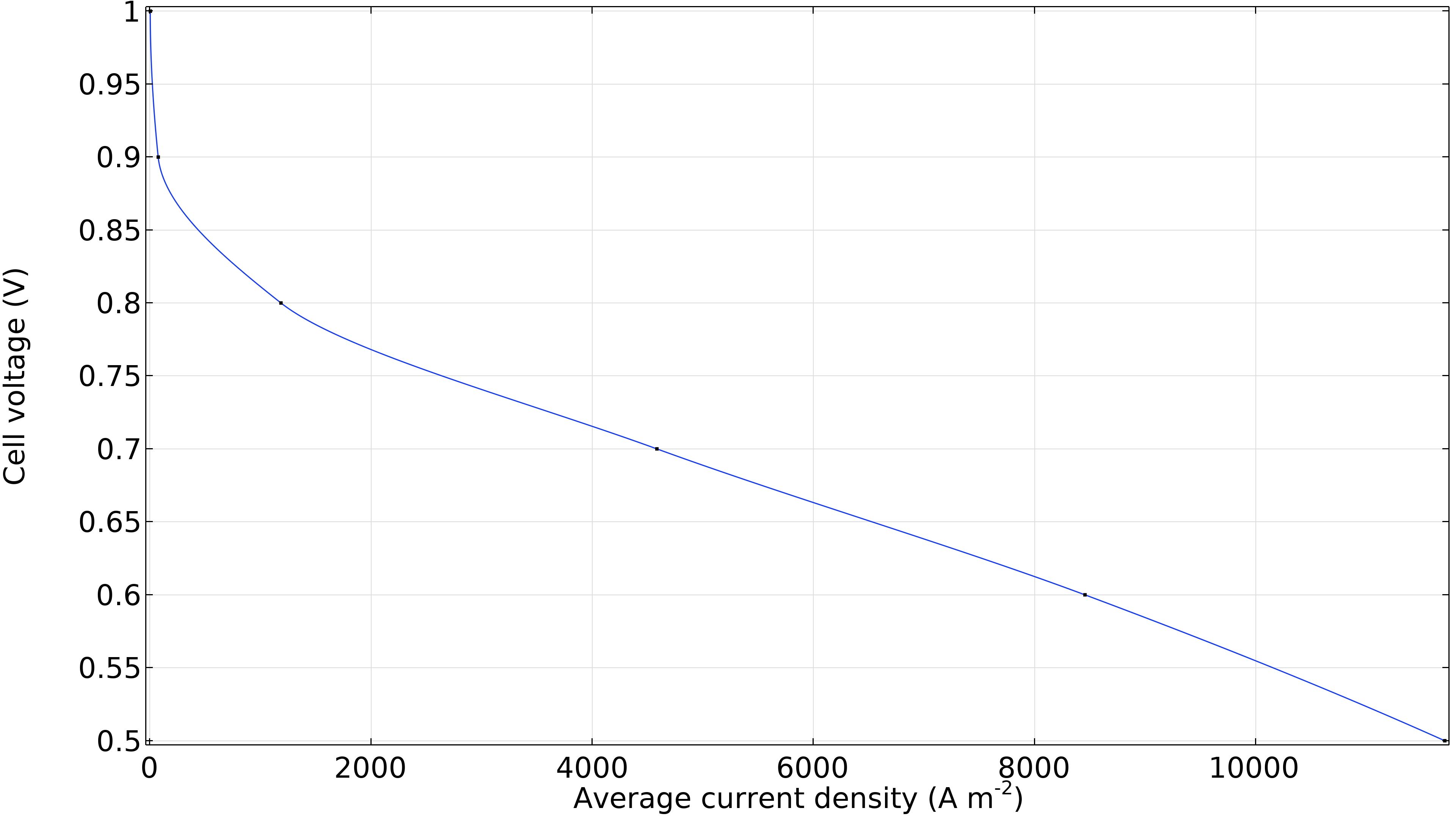
図 12. 平均電流密度の関数としてセル電圧を示す分極曲線.
4. 燃料電池スタック冷却
COMSOL Multiphysics® バージョン 6.1 で導入された燃料電池スタック冷却チュートリアルモデルは, PEM 燃料の熱管理を評価するために使用できます. 5つのセル, 5つの MEA, および 2つのエンドプレートで構成されるセルスタック. 燃料電池スタックのセル内の温度分布が不均一であると, 水蒸気の凝縮が不均一になり, セル間の性能に望ましくないばらつきが生じる可能性があるため, この種の分析は重要です.
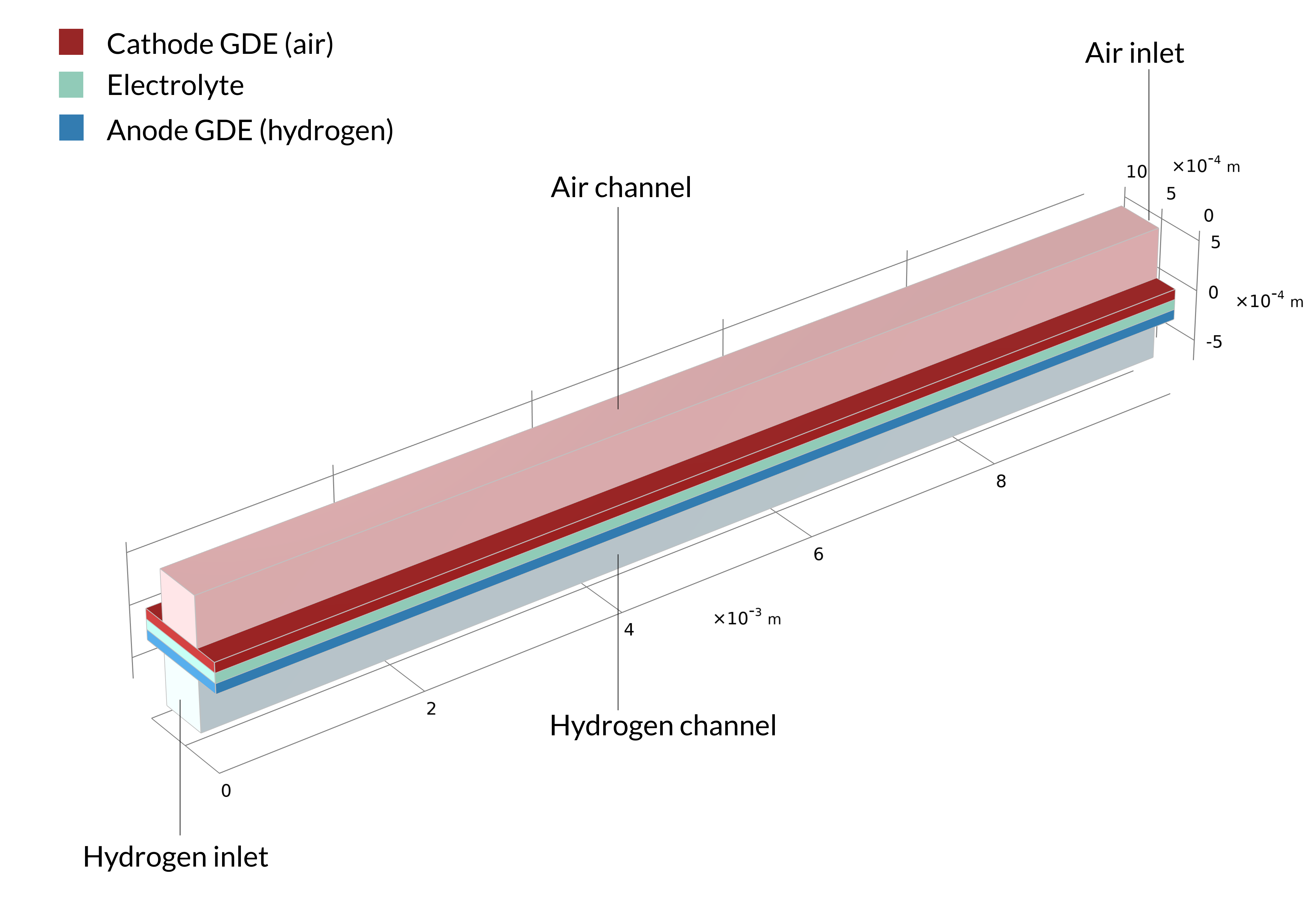
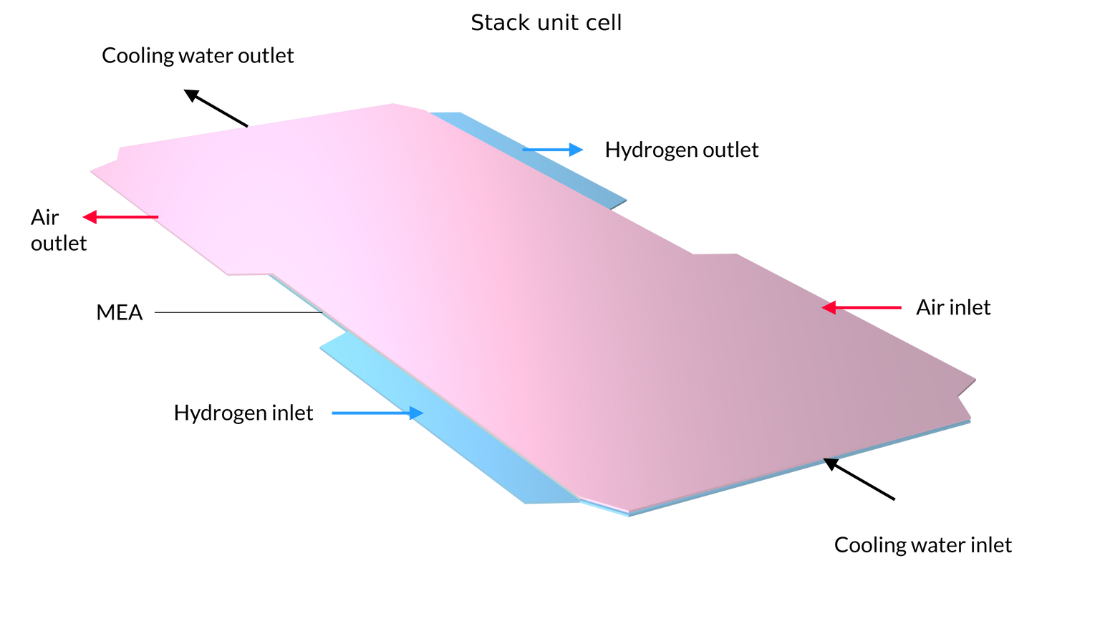
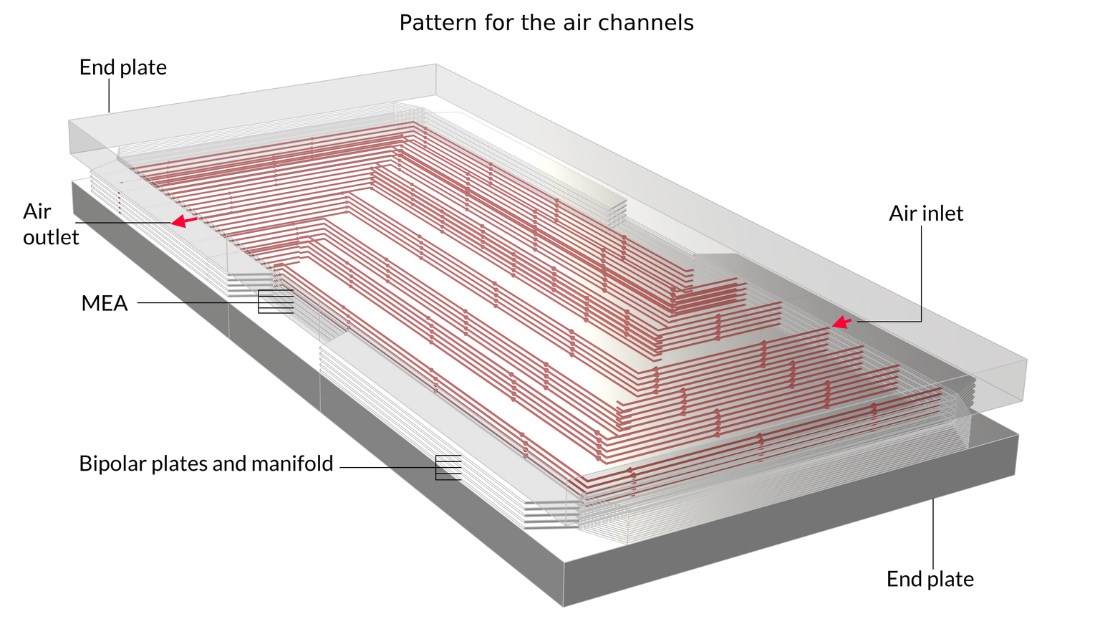
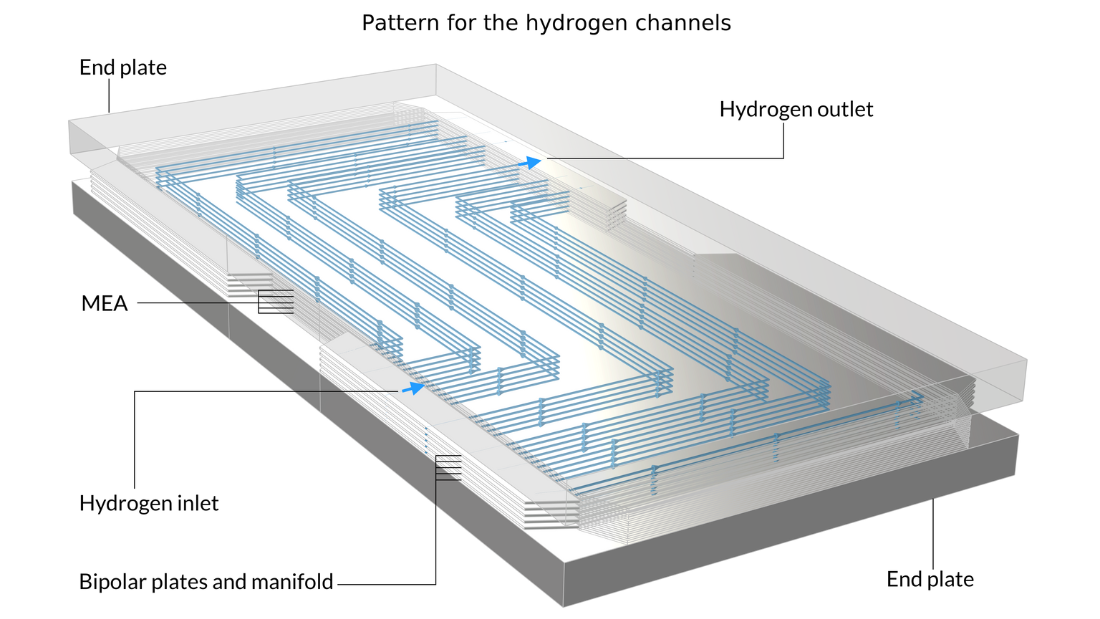
この例では, スタックには液体冷却流体を運ぶバイポーラープレートが中間層に配置されています. 左側の画像は, モデルジオメトリの形成に使用される反復単位セルを示しています. 対照的に, 中央と右側の写真は, 最終的なモデルの形状を示しています. これは, 2つの金属エンドブロックの間に5つの積層された単位セルを挟むことによって構築されています.
図 13. ここでは, 反復単位セル (左) と, 酸素流路パターン (中央) と水素流路パターン (右) を示す 5 つの単位セルを含むスタックの図が表示されます. 左の図でピンクと青で示されている, 空気と水素の流路を含む金属プレートがスタック内で背中合わせに溶接されています. 流路のパターンにより, 冷却水の流路を形成する溶接部の間にスペースが残ります. エンドプレートは構造を保持し, バイポーラープレートと MEA 間の最適な接触を維持するために圧力を加えます.
モデルは次の式を定義します:
- 温度
- 電極および電解質相ポテンシャル
- それぞれの個別のガスコンパートメントにおける反応種の大量輸送
- 気体および液体の流れコンパートメント内の流体圧力と流れ場
- MEAの活性層における電極の反応速度論
このモデルで研究すべき興味深い側面は, スタック内で発生する可能性のある組成, 温度, 電流密度分布の変化です. これらの側面は, バイポーラープレートと MEA の形状に依存します. また, スタックに含まれるセルの数にも依存する場合があります. このモデルにより, ガス流路の構造を反映する異方性特性を備えた多孔質媒体アプローチを使用して, ガス流路の形状を扱うことができます. このようなアプローチをガス流路の完全な記述と比較することで, その精度を検証できます. このアプローチの利点は, 計算コスト (CPU 時間とメモリ要件) を大幅に削減しながら (目的に応じて) 優れた精度が得られることです.
以下でこのモデルの結果の一部を参照し, アプリケーションギャラリで PDF の説明書と MPH ファイルをダウンロードして試してください.
モデル化の結果
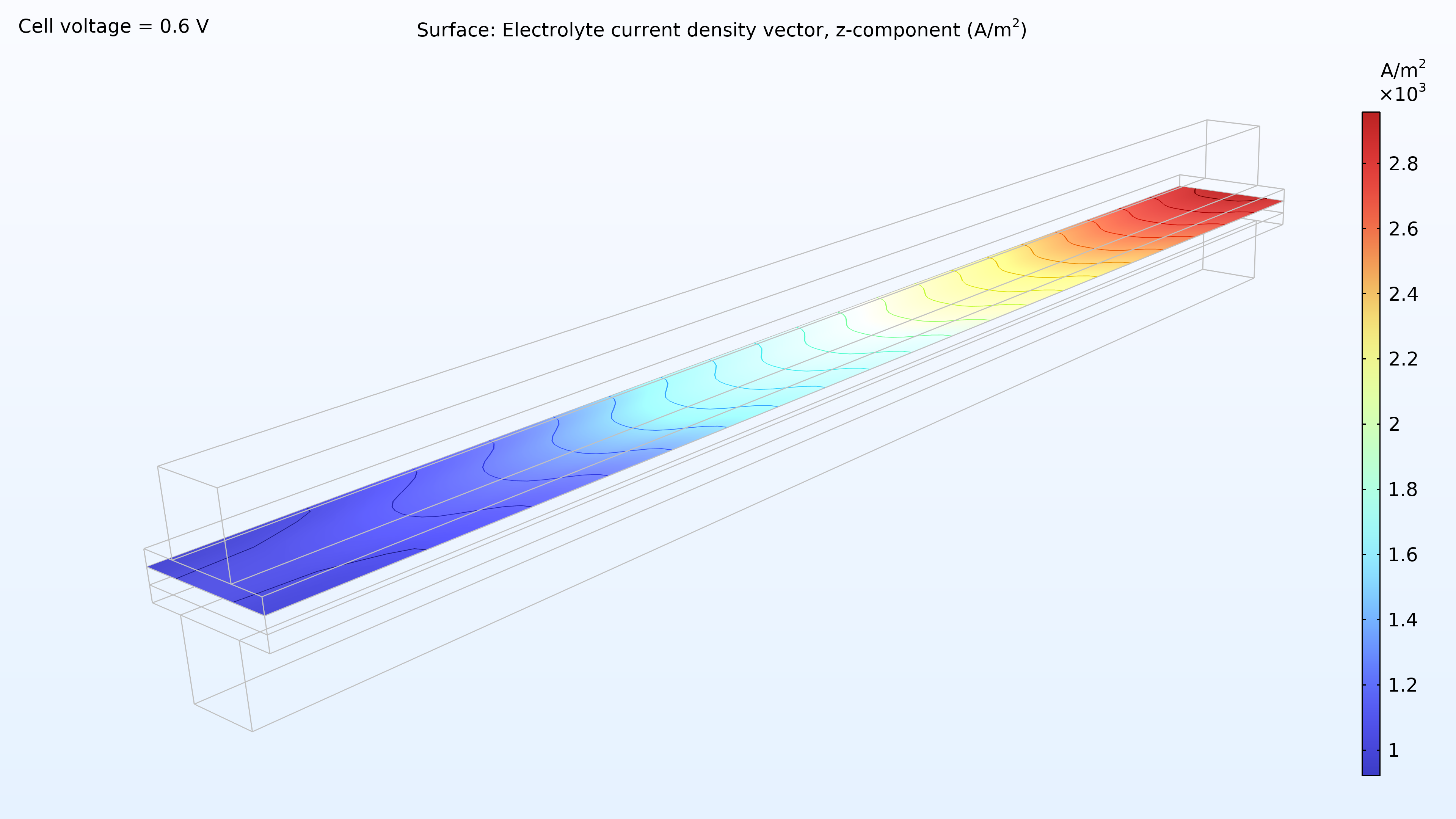
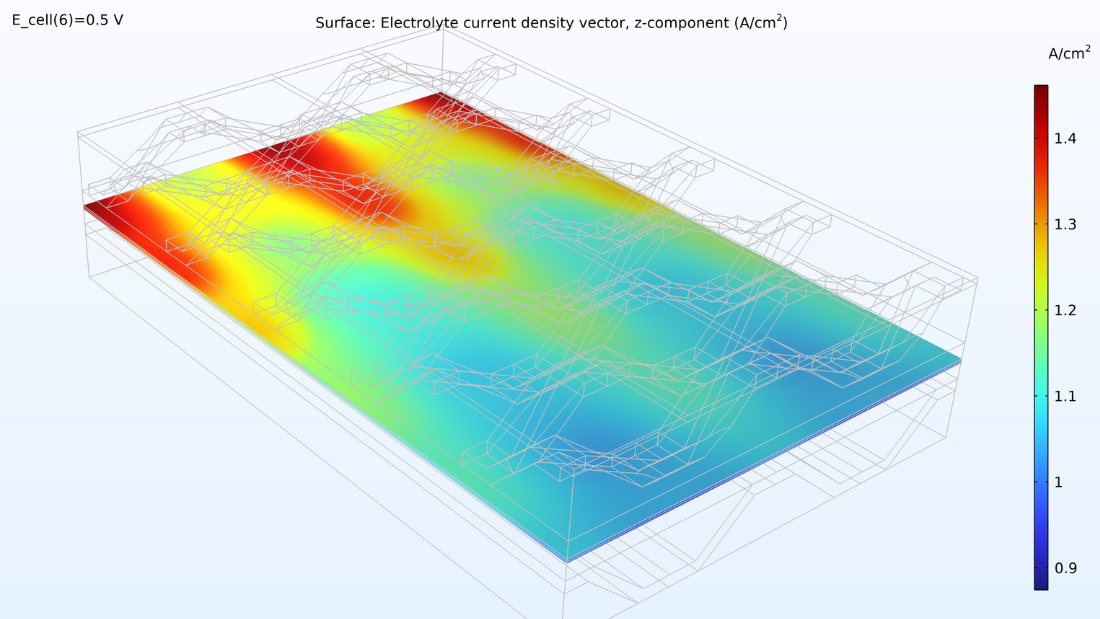
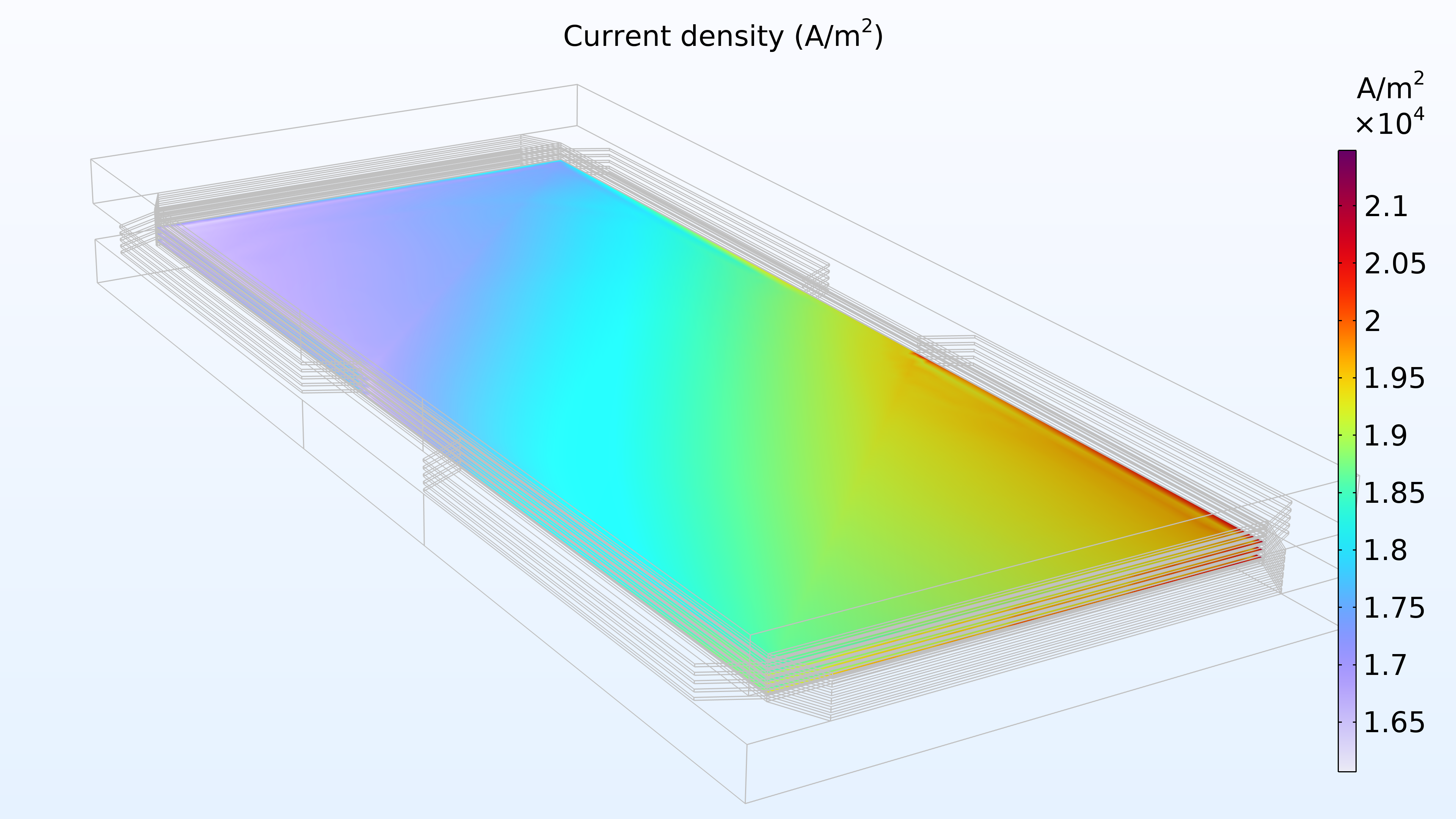
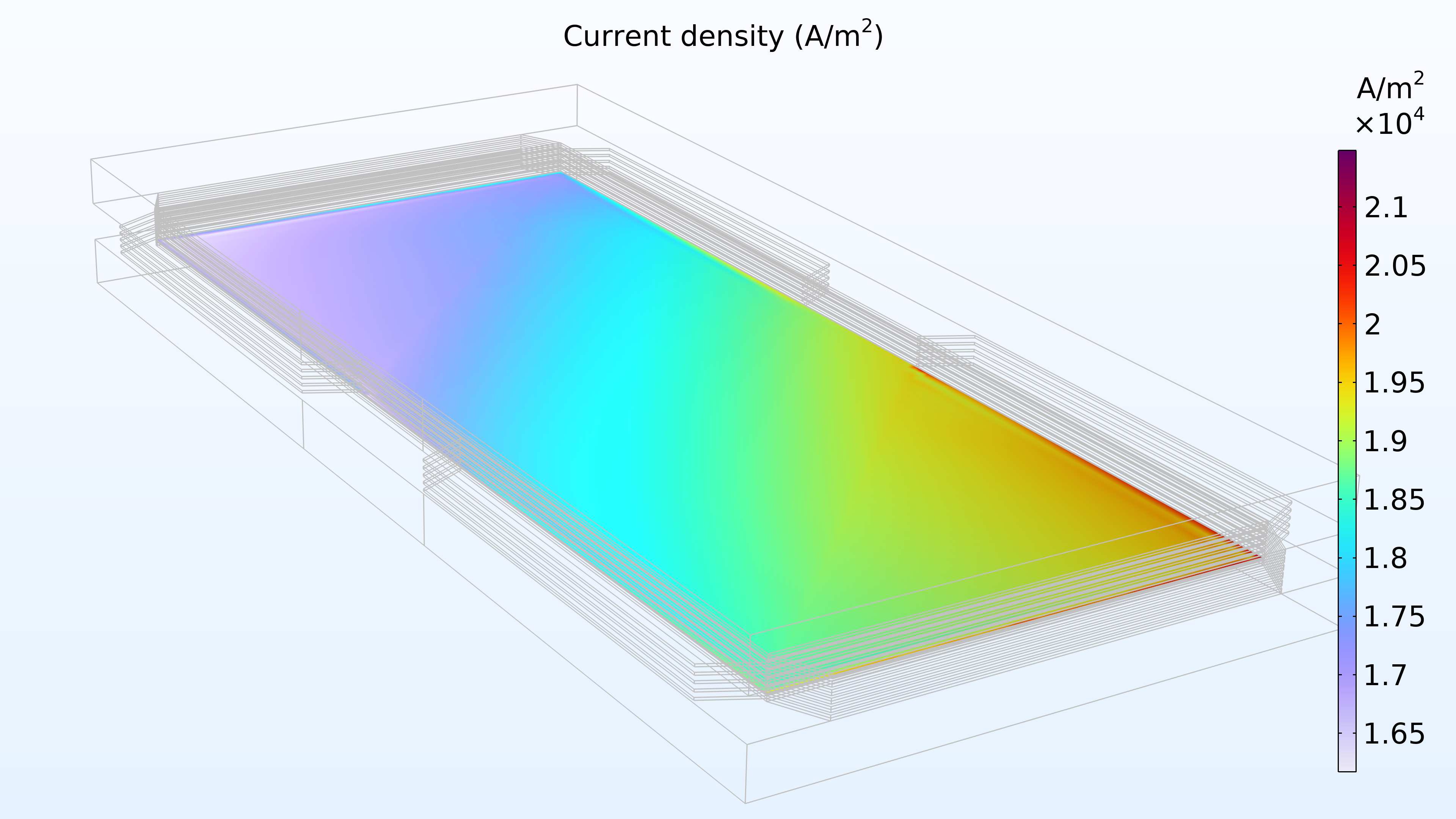
図 14 は, 電極間のメンブレイン内の電流密度分布を示しています. 空気の供給は電荷移動速度を決定すると考えられ, その結果, 空気入口での電流密度が高くなり, 空気出口での電流密度が低くなります. さらに, 電流密度分布はスタックの上部, 中間, 下部でほぼ同一です.
図 14. 上部セル (左), 中間セル (中央), および下部セル (右) のメンブレイン内の電極間の電流密度.
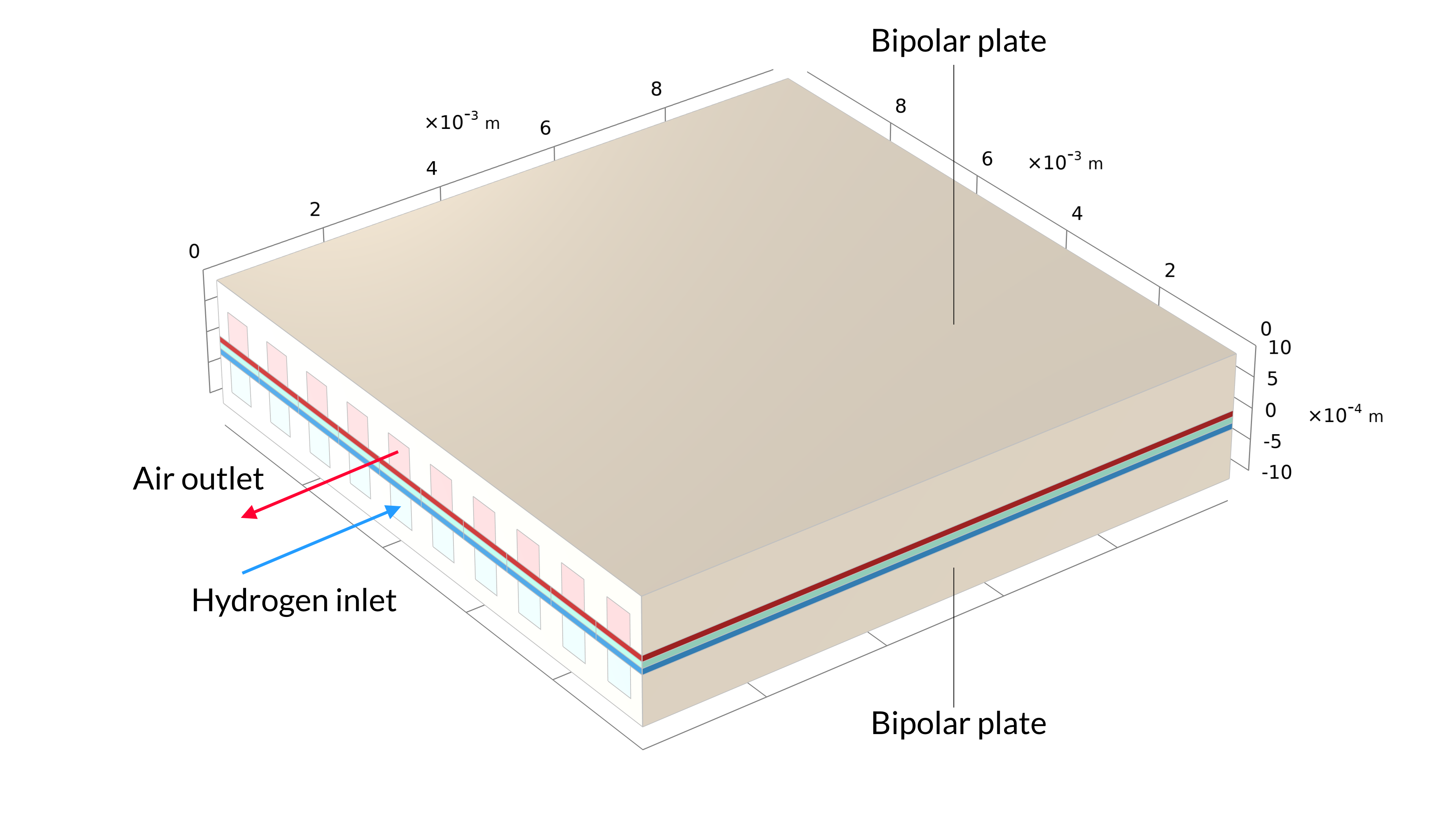
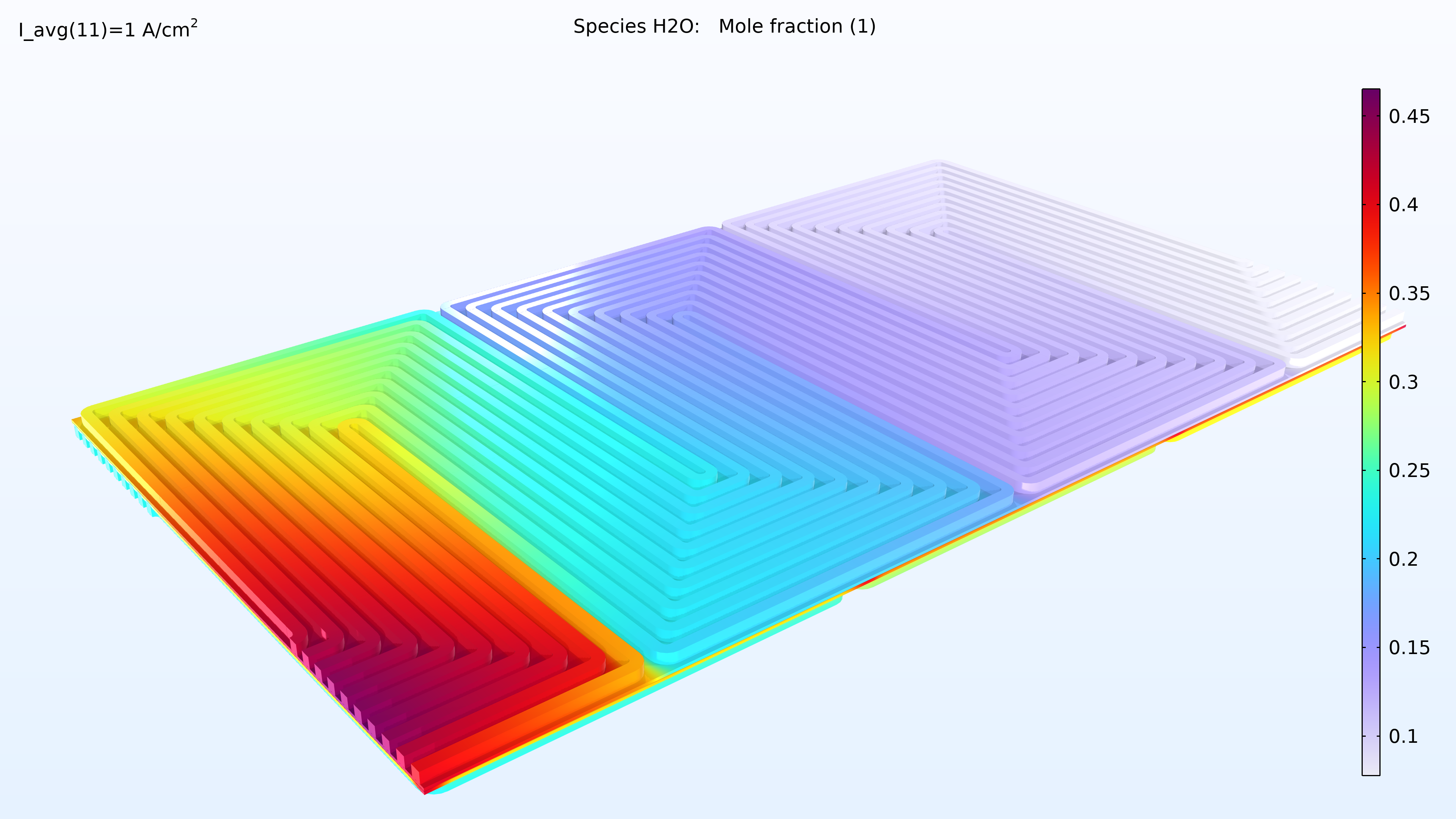
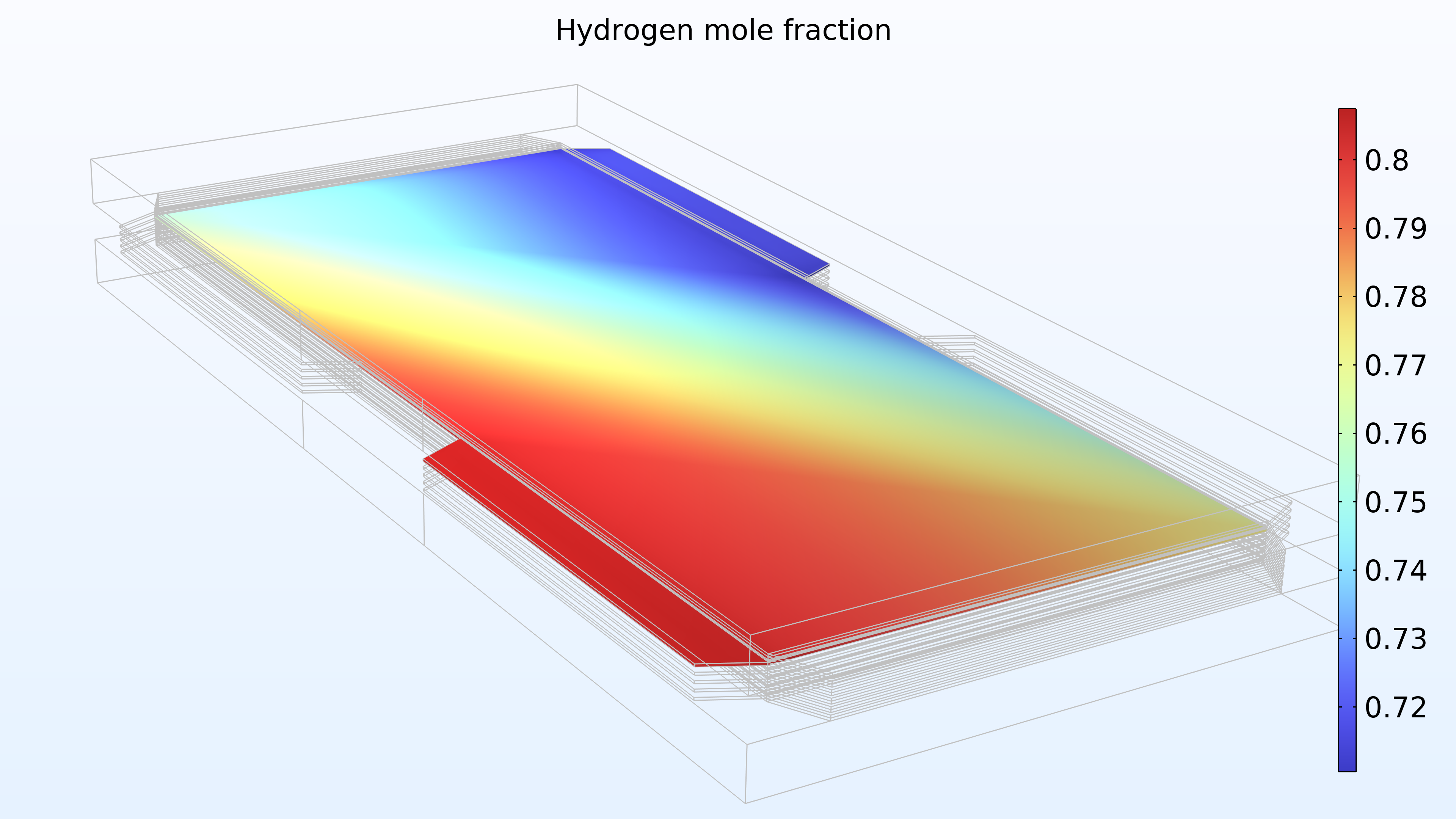
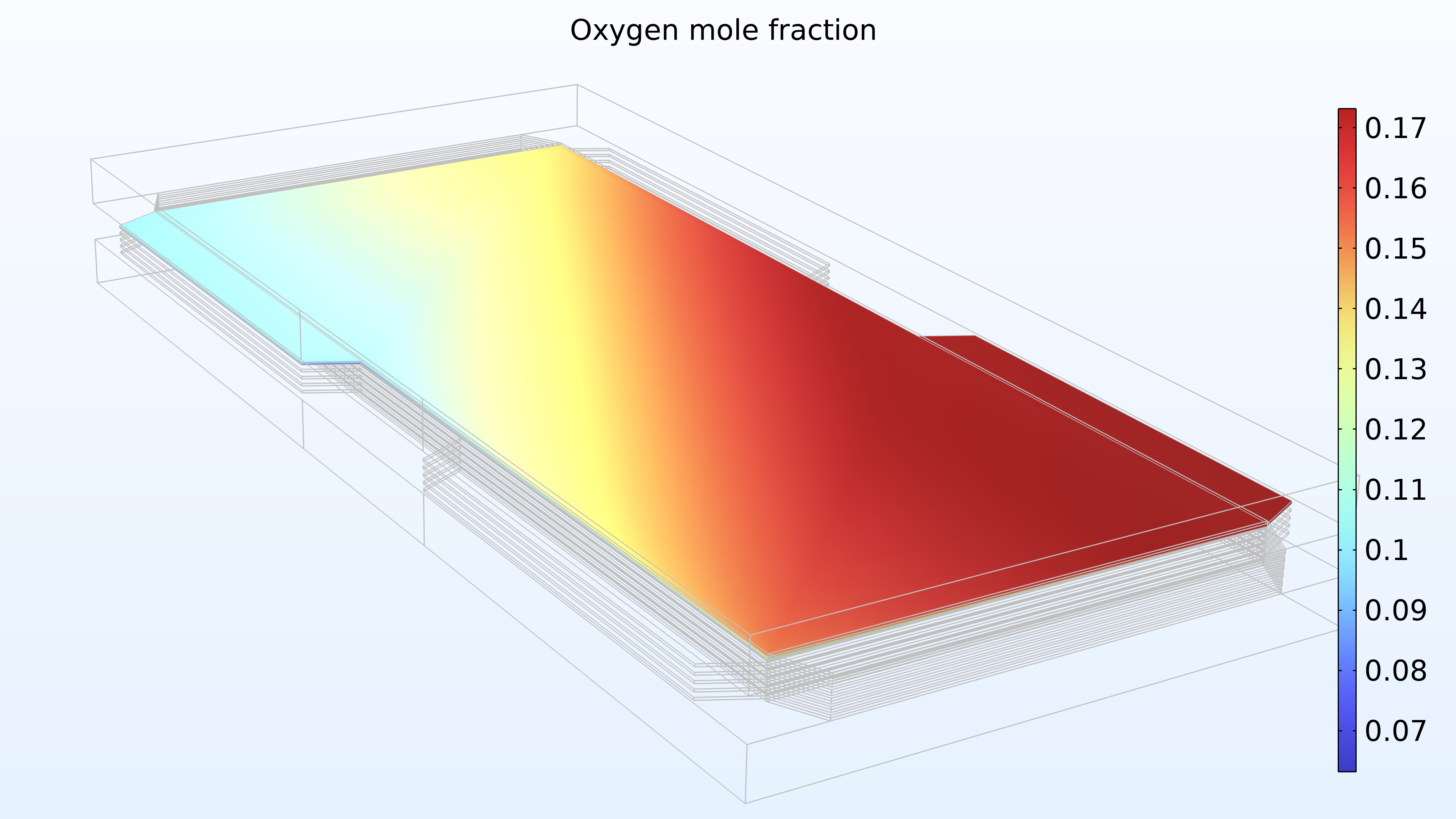
図 15 は, ガス流路と多孔質電極の上部セル内の水素と酸素のモル分率を示しています. 予想通り, 上記の電流密度分布は酸素モル分率のプロファイルを反映しています. 酸素は水素よりも大幅に消耗されることに注意してください. さらに, 酸素はカソードの厚さに沿って減少しますが, 水素のモル分率はアノードの厚さに沿ってほぼ一定です.
図 15. スタックの一番上のセルの水素モル分率 (左) と酸素モル分率 (右).
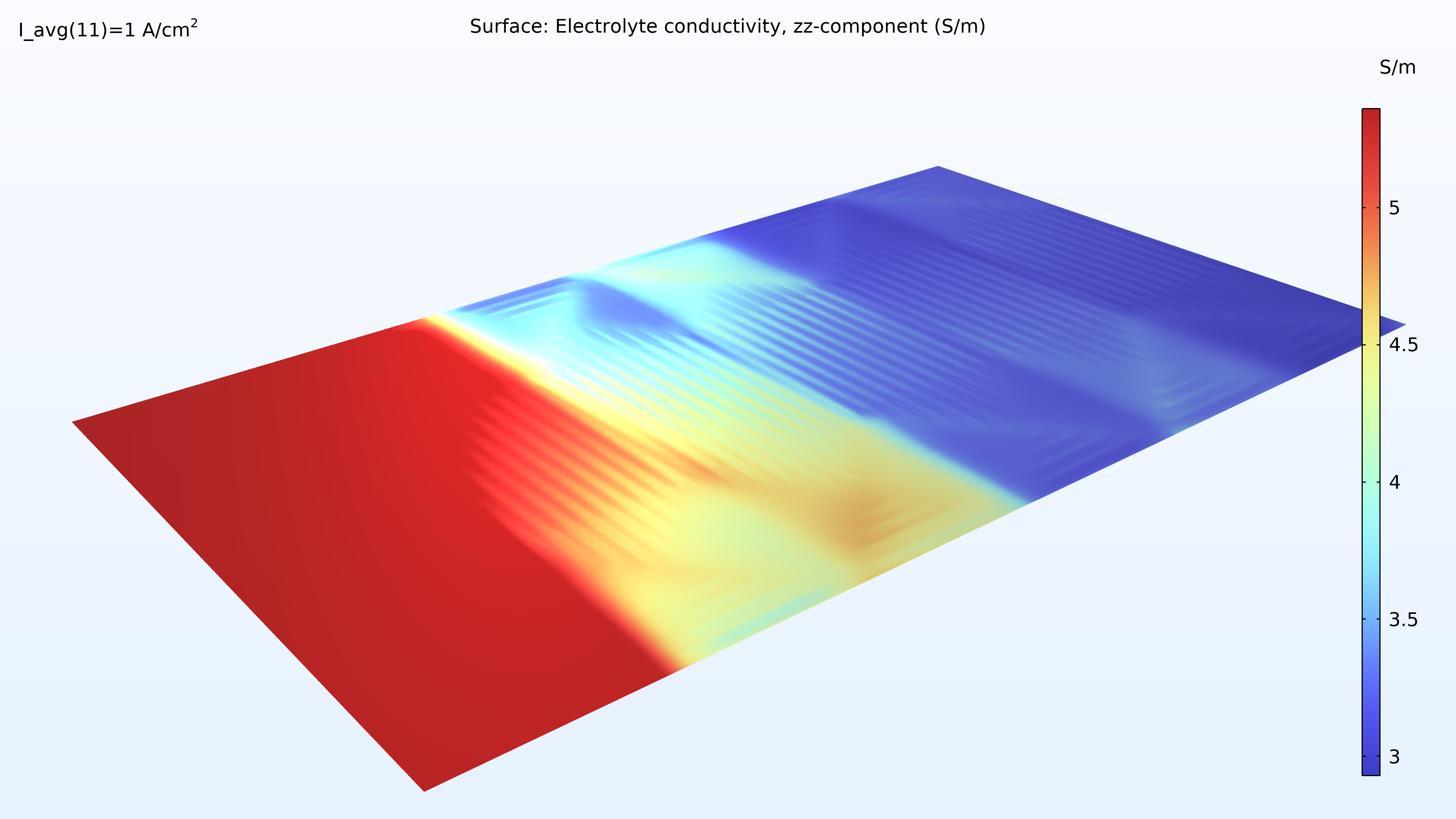
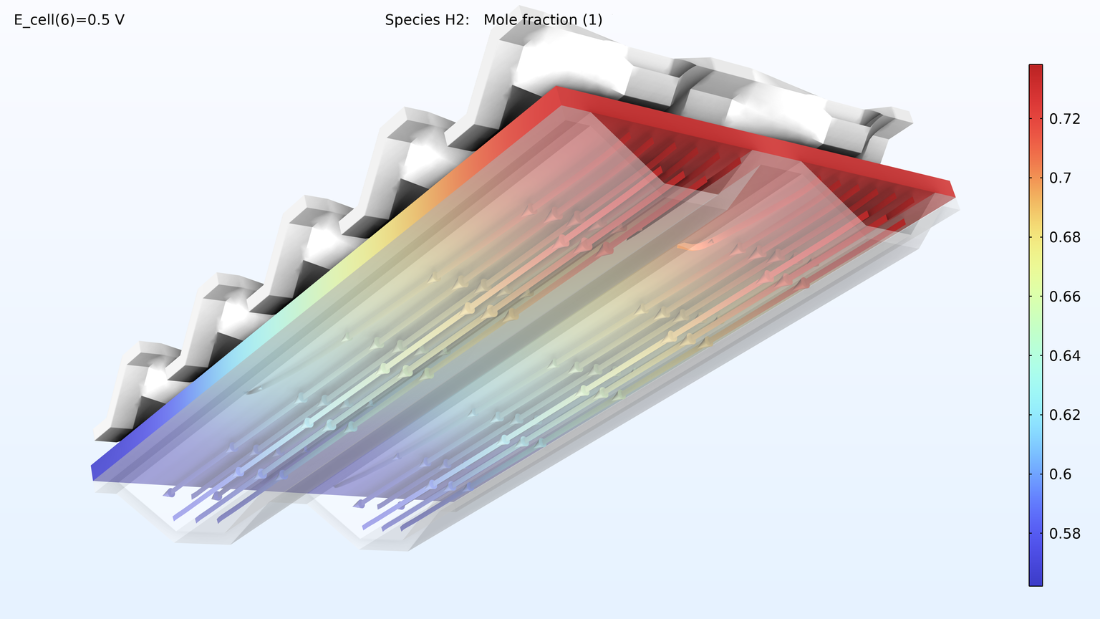
図 16 は, カソードガス流路と電極, メンブレイン, アノード流路と電極のスタックの上部セルの温度を色の凡例で右から左に示しています. メンブレイン内の温度は高くなりますが, これは膜の電気伝導率と熱伝導率が低いため予想されます. また, 冷却水の方向に温度が上昇することも予想されます.
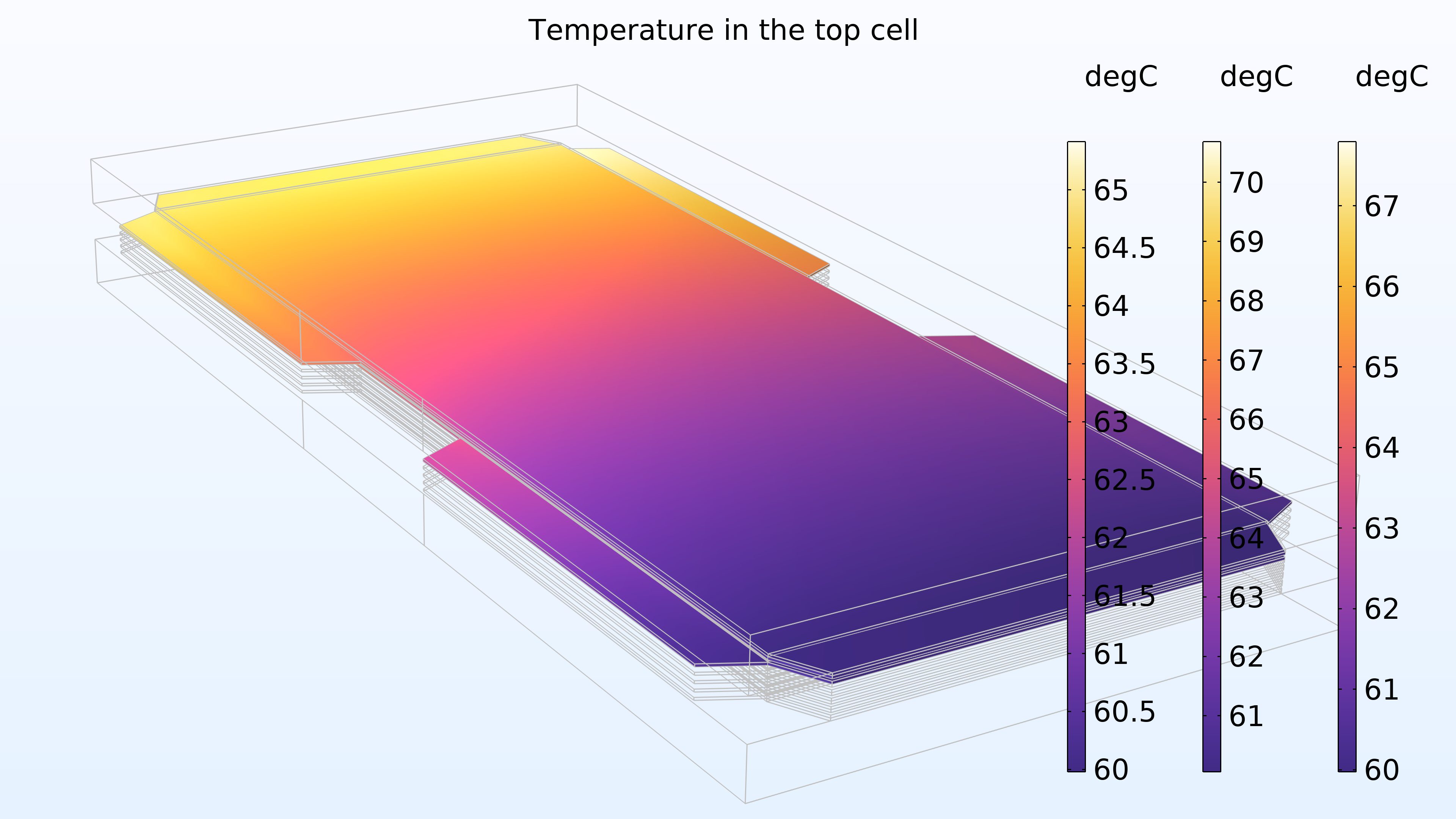
図 16. スタックの最上位セルの温度.
図 17 はスタック内の温度を示しています. 最高温度は中央セルのメンブレインで得られます. この位置はエンドプレートから最も離れており, ある程度の冷却に寄与します. バイポーラープレートの冷却流路も冷却を提供します. さらに, 温度分布は 2 つのエンドプレートで同一であることがわかります.
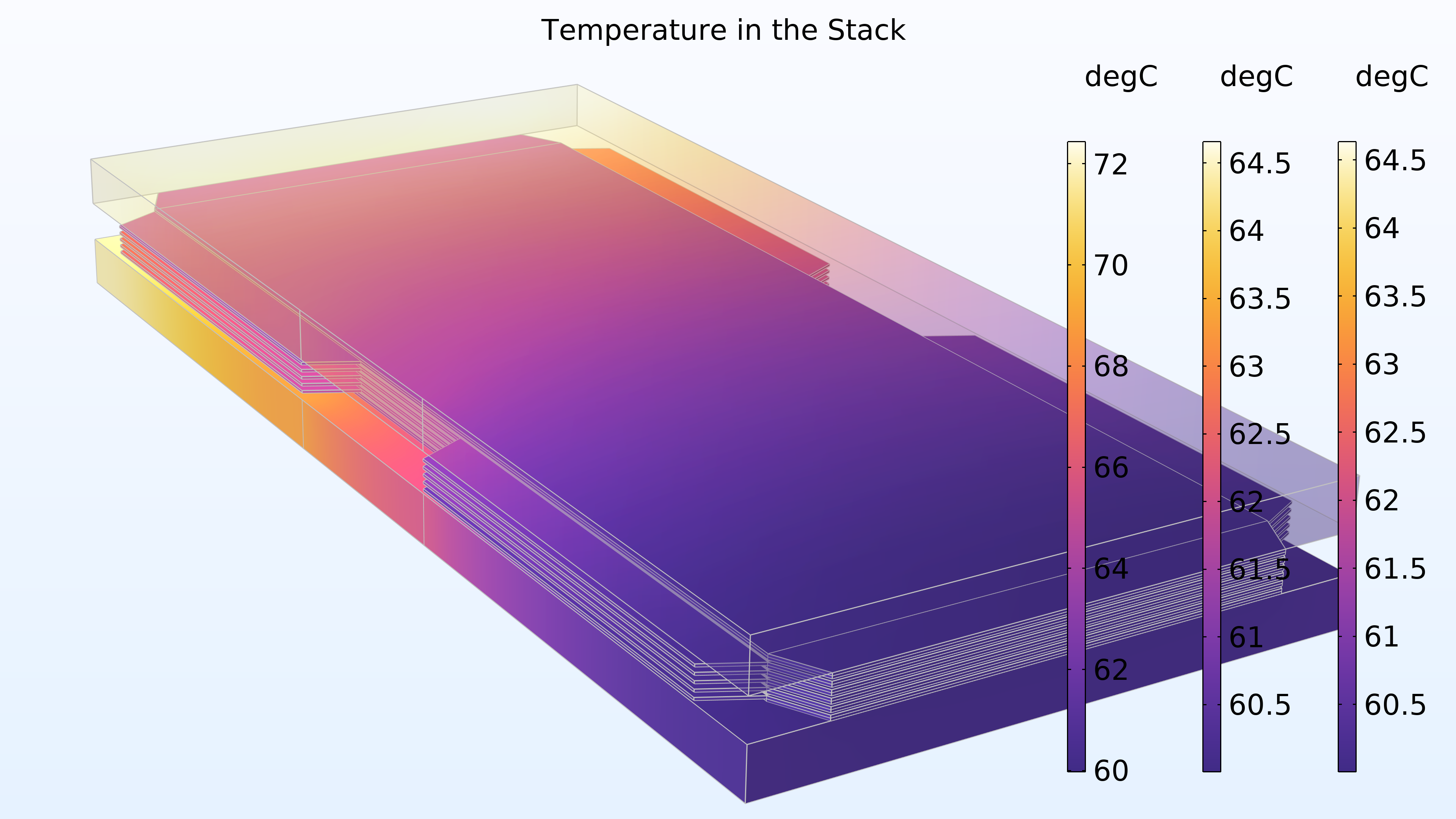
図 17. スタック内の温度. 右と中央の色の凡例はエンドプレートに対応し, 左の色の凡例は細胞に対応.
モデルには, スタックの高さに沿ってわずかな変化が見られます. これは, より多くのセルを積層すると変わります. その結果, セルの高さに沿って酸素または水素が減少し, マニホールド内のガス流路も変化します.
次のステップ
これらは, モデリングとシミュレーションを燃料電池開発にどのように使用できるかのほんの数例ですが, 他にもたくさんあります. シミュレーションを使用して燃料電池をより深く理解することで, エンジニアはこれらのセルの全体的な効率, 出力, 信頼性を向上させ続けることができます.
ここで示した例はすべて, 通常, 燃料電池および電解槽モジュールを使用して構築されることに注意してください. このモジュールの詳細については, こちらをご覧ください. これは, 水素燃料電池, 工業用電解装置などのモデリングに使用できます. 下のボタンをクリックしてください!
チュートリアルモデルを試す
上記のチュートリアルモデルを自分で使ってみてください. 以下のリンクをクリックすると, アプリケーションギャラリのエントリに移動し, 付属の MPH ファイルをダウンロードできます.







コメント (0)