
連続回転対称性を持つオブジェクトの電磁波散乱シミュレーションは, 3D ではなく 2D 軸対称モデルで実行することで, 計算時間やリソースを大幅に削減することができます. このブログでは, 円筒座標での平面波展開を利用して, 2D 軸対称モデルで任意の平面波入射をシミュレーションする方法についてご説明します.
電磁場シミュレーションにおける散乱場定式化
基本的には, 伝播する電磁波がオブジェクトに衝突すると, オブジェクトとの相互作用により, 元の波の伝播特性が変化します. この種の散乱現象は, RF, マイクロ波, 光工学の分野で大きく注目されています. 電磁波散乱の正確なシミュレーションを行うため, COMSOL Multiphysics® ソフトウェアのアドオンである “RF モジュール” と “波動光学モジュール” は, 便利な “散乱場” 定式化を提供しています. ここで, 全場はユーザー定義の背景場と, シミュレーションで解かれる散乱場の和として記述されます. 背景場の一般的なオプションには, 平面波とガウシアンビームがあります. 任意の背景場を柔軟に定義することもできます.
円筒座標での平面波展開
様々な背景場の中で, 最もよく使われるのが平面波です. しかし, 2D や 3D モデルの場合と異なり, 2D 軸対称モデルの背景場を, 任意の方向に伝播する平面波として単純に設定することはできません. これは, 回転対称性を破ることになるためです. 幸い, これからご紹介する裏技を使えば, 2D 軸対称モデルでも平面波の背景場を実現することができます.
ここで, 次のように与えられる一般的な平面波背景場を考えてみましょう.
一般性を失わず, \bm{k} は xz 平面上にあると仮定し, \bm{k} と z 軸線との間の角度は \theta で与えられます. 簡略化のため, P 偏光入射のみを考えますが, S 偏光も同様の方法で実装可能です. P 偏光の場合, \bm{E_0}=E_0 (cos \theta \bm{\hat{x}} + sin \theta \bm{\hat{z}}), そして \bm{k} = k (sin\theta \bm{\hat{x}} – cos\theta \bm{\hat{z}}) であり, ここで, k=\omega/c となります. したがって, 平面波は次のように書くことができます.
ここで, \phi=atan\frac{y}{x} は方位角, そして r=\sqrt{x^2+y^2} です. ここでは簡略化のため, 因子 e^{i\omega t} を省略しますが, 暗示されています. 展開するには, 2つの重要な要素が必要です. 次の円筒座標での平面波展開, 部分波展開
と, デカルト座標から円筒座標への座標変換です.
ここで, J_m は第1種ベッセル関数の次数 m です. 先の式といくつかの代数を組み合わせると, 次のようになります.
これでようやく, 平面波の背景場をモード番号 m の方位角モードの無限和として円筒座標上で書くことができます. つまり, 2D 軸対称シミュレーションに実装することができるということです. さらに, 正の m と負の m は位相因子が異なるだけなので, 原理的には m=0 から m=N まで和を求めれば良いことになります. 例えば, 背景場の \bm{r} 成分は次のように書くことができます.
ここで, \chi は m=0 に対して \chi(m)=1, m>0 に対して \chi(m)=2 となる階段関数です. 和は無限大に拡張されますが, 散乱の大きさが波長と同程度であれば, 結果はわずか数項で収束します.
長球の散乱解析
具体的な例として, COMSOL Multiphysics を用いて, 5 THz から 50 THz までの赤外周波数範囲における銀の長球の散乱を解析します. まず, 半軸 a=2\ \mu m と b=5\ \mu m の長球を作成します. 該当する周波数範囲における銀の光学特性は, 材料ライブラリから見つけることができます. この周波数範囲では銀の導電率が高く, それでも小さな損失を考慮したいので, 回転楕円体の表面には “インピーダンス境界条件” を適用することができます. 外側の境界には完全整合層 (PML) を追加して, 外向きの放射を吸収します.
次に, 背景場の各成分を, 固定の方位角モード番号 m で以前に導出したように定義し, 散乱の定式化における背景場として使用します. “変数” サブノードでは, ポインティングベクトルの表面積分である散乱断面積も定義しています. (これについては後で詳しく説明します.)
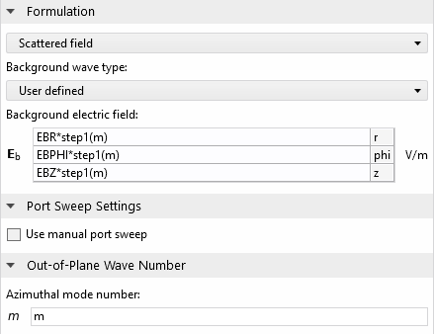
散乱場定式化が使用されています. 階段関数では, 正負の m が考慮されています.
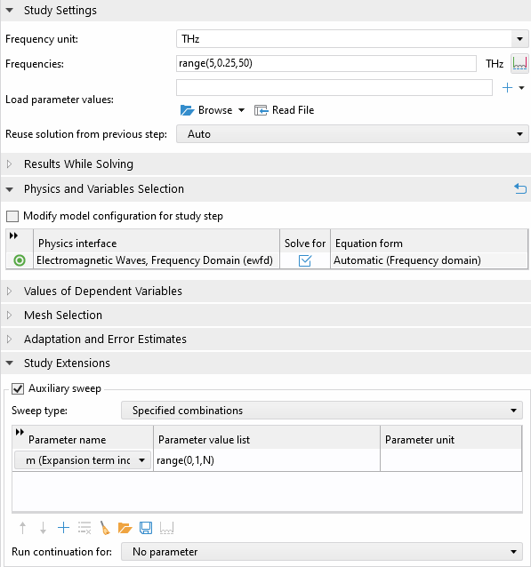
最後に, 周波数スイープを5 THz から50 THz まで0.25 THz 刻みでスイープするように設定し, 補助スイープで m を0から N までスイープします. より一般的なパラメータースイープの代わりに周波数スイープと補助スイープを使用することで, シミュレーションの速度を向上させることができます.
要素サイズを極端に細かく設定しても, 広帯域シミュレーションはわずか5分程度で終了します. ポスト処理では, 全散乱場と全背景場の両方を可視化し, 平面波に近いことを確認するために, いくつかの裏技を使用します. そのために, ミラー 2D データセットを利用します (詳細は関連モデルを参照). このようにして, \phi と \pi-\phi における磁場分布を同じプロットでプロットすることができます. 全散乱場は, 各展開項の散乱場の和です. 例えば, 30 THz, \phi=0 における全散乱場のノルムは, 以下のように計算できます.
sqrt(abs(sum(withsol('sol1', ewfd.relEz*cos(m*0), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2 + abs(sum(withsol('sol1', ewfd.relEr*cos(m*0), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2 + abs(sum(withsol('sol1', j*ewfd.relEphi*sin(m*0), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2)
ここでは, “withsol” 演算子を用いて, 周波数30 THz, 方位角モード番号 index の散乱場を選択しています. さらに, 各解の寄与を合計するために “sum” 演算子を使用しています.
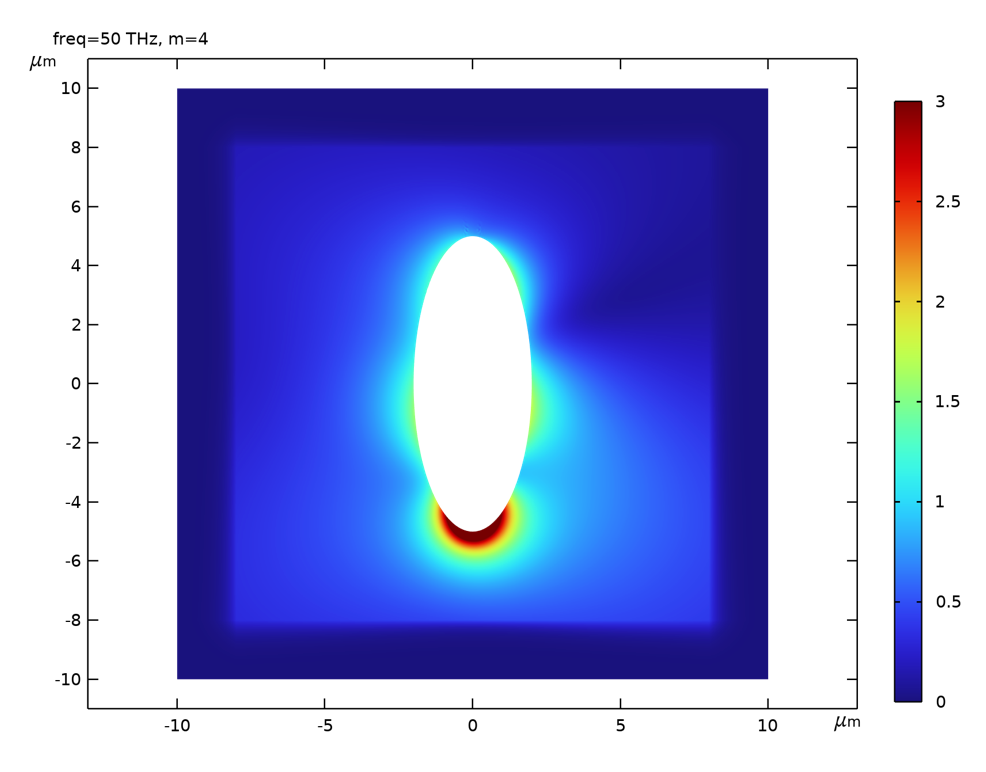
各展開項からの寄与を合計した30 THzでの全散乱場のノルムの 2D プロット.
また, “回転 2D” データセットを使用して, 3D で散乱場をプロットすることもできます. デフォルトでは, “回転 2D” データセットは, 再評価のボディを実装するだけであり, 方位角の依存性は無視されることにご注意ください. 正しい \phi 依存性は, まず “回転 2D” データセットの設定の “高度” タブで “変数の定義” を有効にすることで手動で追加することができます. これにより, 方位角の rev1phi という変数が有効になります. そうすると, 3D での全散乱場のノルムの正しい式は, 以下のようになります:
sqrt(abs(sum(withsol('sol1', ewfd.relEz*cos(m*rev1phi), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2 + abs(sum(withsol('sol1', ewfd.relEr*cos(m*rev1phi), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2 + abs(sum(withsol('sol1', j*ewfd.relEphi*sin(m*rev1phi), setind(m,index),setval(freq,30[THz])), index, 1, N+1))^2)
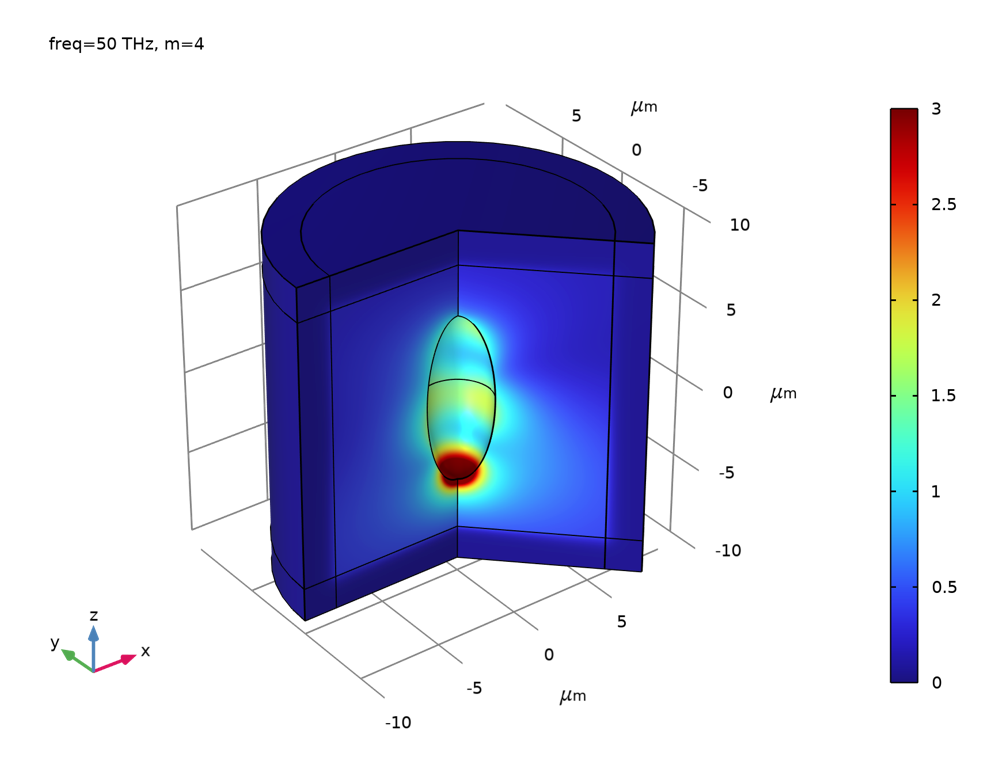
“回転 2D” データセットによる同じ磁場の 3D サーフェスプロット.
背景場は散乱場と同じようにプロットすることができます. 展開で N=4 のみがあるとき, 散乱場の周りの背景場が平面波と区別がつかなくなることがわかります.
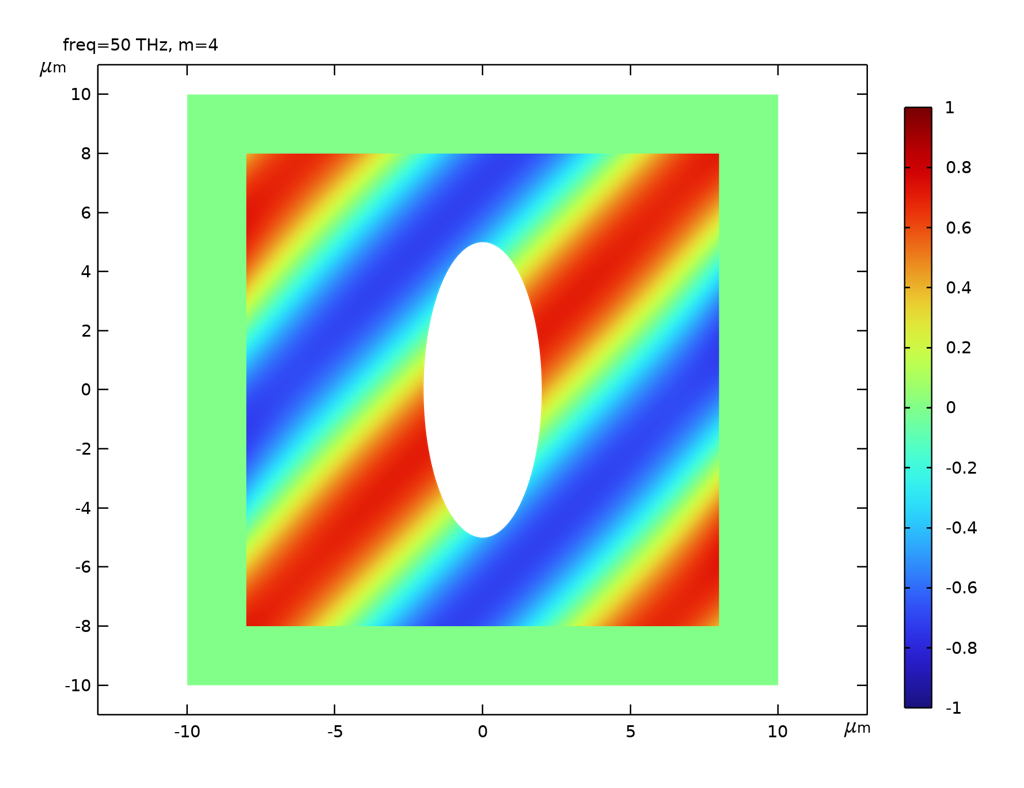
各展開項からの寄与を合計することによって得た, 全背景場の z 成分.
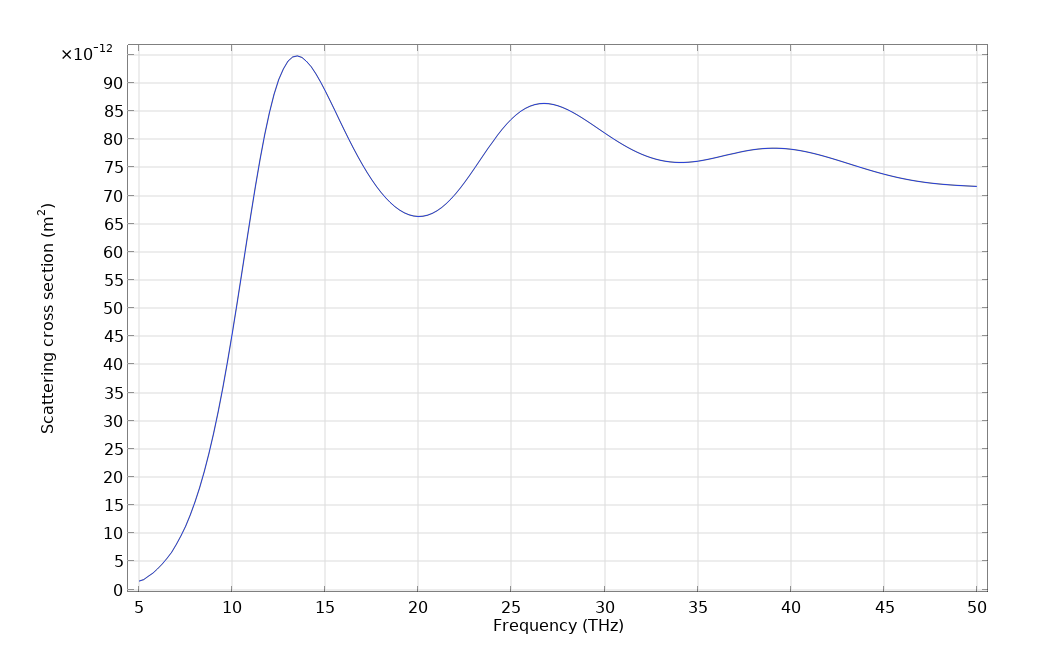
最後に, 散乱断面積を周波数の関数としてプロットします. “変数” で散乱断面積の式を定義したことに注意してください. 全散乱断面積は次のように計算することができます.
-withsol('sol1', sigma_sc, setval(m,0),setval(freq, freq))-sum(withsol('sol1', 0.5*sigma_sc, setval(m,val),setval(freq, freq)),val,1,N)
マイナス記号は, 回転楕円面の面法線が内側を向いているためです. m>0 の項の乗法因子0.5は, 各項が正と負の m の和であるため, エネルギーの倍増を補うためのものです. 通常, 全散乱断面積は, 各展開項で計算されたものを単純に合計したものではありません. これは, 散乱断面積とポインティングベクトルが, 磁場ではなく, エネルギーに直接関連しているためです. エネルギーは磁場の2乗に比例します. したがって, 多くの項の和を2乗すると, 2乗の和に加えて交差項が出てくるのです. 幸運なことに, 我々が見ているケースでは, 方位角モードが直交しているため, 交差項はすべて消えます. つまり, \phi で積分すると, 交差項はすべてゼロになるということです. その結果, 全散乱断面積は各展開項からの和となります. このように, 長球の散乱断面積は回転楕円体のそれと定性的に似ており, これはよく知られる Mie 散乱理論 の結果です.
最後に
このブログでは, 平面波励起下での回転体の散乱特性を 2D 軸対称モデルでシミュレーションする方法をご紹介しました. この方法でシミュレーションを実行すると, 完全な 3D シミュレーションと比較して, 非常に多くのメリットがあります. 計算メモリや時間のコストが少なくとも1桁は小さくなります. そのため, 細かいメッシュを使用することで,非常に高いシミュレーション精度を実現することができるのです. また, 今回は明示的にご紹介しませんでしたが, 多数のパラメーターをスイープする必要がある一方で RAM の必要量は少ないため, “バッチスイープ” 機能を使って複数のシミュレーションを同時に実行することも大きなメリットになると思われます. 今回のモデル例では, 散乱場と散乱断面積の計算を示しましたが, 遠方場放射パターンなどの散乱問題に関連するその他の重要な量も同様に導出することができます. 最後に, 様々な物理量を計算するときに, モード番号に関連する位相因子を追跡するために注意を払う必要があることに気を付けなければなりません.
試してみましょう
下のボタンをクリックすると, アプリケーションギャラリのエントリに移動し, “平面波展開” モデルをご自身でお試しいただけます.







コメント (0)