
COMSOL Multiphysics®半導体フィジックスインターフェースの金属コンタクト境界条件に接触抵抗の寄与をオプションで追加することができるようになりました. このブログでは, この新機能を利用したクロスブリッジケルビン抵抗器のベンチマークモデルについてご説明します.
モデル構造
クロスブリッジケルビン抵抗構造は, 金属ー半導体コンタクトの接触抵抗を評価するために一般的に使用されます. ここでは, 参考文献1に記載されている一連のテスト構造について検証します.
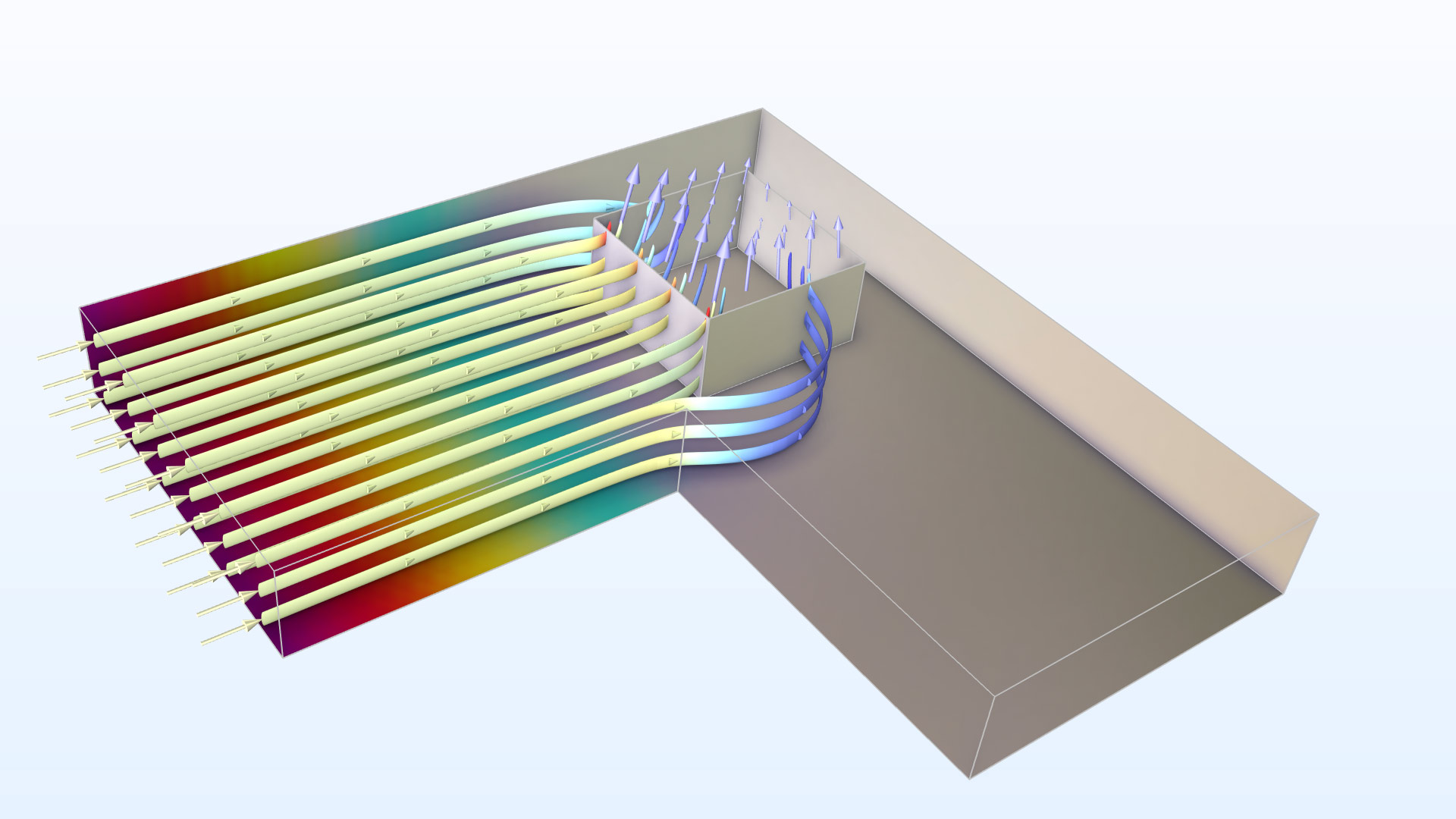
接触抵抗測定用クロスブリッジケルビン抵抗の電位 (色) と電流密度 (矢印と流線) のシミュレーション.
構造の中心は, 上のスケッチに示すように, “L” 字型にパターン化された厚さ n+ 5000 Å のドープポリシリコン層です. 電流は ”L” の左アームに注入され, 矢印で示すように, 四角いコンタクトウィンドウから上の金属層に流れます (金属層はスケッチでは明示的に表示されていません). ブリッジ電圧計で ”L” の右アームと金属層との間の電圧降下を測定します.
この構造では, 直接測定可能な量, ケルビン接触抵抗 R_c (SI 単位: Ω) を得ることができます. これは電圧降下を, コンタクトウィンドウを流れる総電流で割ることによって得られます. しかし, この抵抗値は, テスト構造の寸法によって変化するため, 接触の特性評価に適した量ではありません. これは, コンタクトウィンドウを流れる電流密度の分布が不均一であることに原因があります (上のスケッチの矢印の異なる長さが示しているこの現象のことを電流集中効果と言います).
金属ー半導体接触の性質は, もう一つの量, 特性接触抵抗 \rho_c (SI単位:Ω m2)でよりよく特徴付けられます. これは, 局所電圧降下を無限小の接触面積要素内の法線方向の電流密度で割ったものと定義されます. この量は直接測定することができないため, 数値シミュレーションによって測定したR_cの値から抽出する必要があります.
特性接触抵抗の抽出
テスト構造の寸法を変化させたときに R_c の値がどう変化するかについて, 参考文献1の中では二種類の計測を行った結果が報告されています. 最初の実験では, コンタクトウィンドウ (l) のサイズを5.0~65 μm に変化させ, “L” の2本のアームの幅 (拡散タップ幅, w) は l より5 μm 大きく維持されるようにしました. もう一つの実験では, 拡散タップ幅 w を7.5〜60 μm に変化させ, コンタクトウィンドウのサイズ l を5 μm で一定にしました. これらの実験から得られた R_c–l と R_c–w のデータは, \rho_cの値を変えて数値シミュレーションを行い, 実験データとシミュレーションした R_c–l と R_c–w の曲線との最適なフィッティングを調べることにより, 特性接触抵抗 \rho_c を抽出することができます.
参考文献1の著者らは, 数値シミュレーションのために 2D 近似モデルを選択しました. 2D モデルについては, 参考文献2にて詳細に説明されています. 簡単に説明すると, 半導体モジュールが提供するものと同様の 3D モデルから始め, ショットキーバンドの屈曲と少数キャリア効果を無視し (理想的なオーミック接触を仮定), 多数キャリアのみを考慮します. 金属の導電率は半導体よりもはるかに高いため, 金属内の電位はコンタクトウィンドウ全体で均一であると想定しています.
近似 2D モデル
3D モデルを近似 2Dモデルに簡略化するために, 半導体の導電率は面内方向で均一であると仮定し, 導電率の厚み方向依存性はシート抵抗 (SI 単位: Ω) のパラメーター R_s に一本化しました. 金属が接地され, 伝達長 l_t (\equiv\sqrt{\rho_c/R_s}, SI 単位: m) が n+ ドープ層の厚さより大きいという仮定のもと, 新しい変数, 導電率加重平均電位 V_{2D} (SI 単位: V)に対して単純な 2D 方程式を導くことができます. 式は, コンタクトウィンドウの下では次となります.
(1)
また, 他のすべての場所では次となります.
(2)
ラプラシアン演算子の添え字 t は面内 (接線) 方向を表しています. この 2D モデルにおいて, 面内電流密度は次のように評価され,
(3)
コンタクトウィンドウを通る法線方向の電流密度は次の式で与えられます.
(4)
チュートリアルの例では, 3D と 2D の両方のモデルを構築し, 結果を比較しています.
3D モデル設定
3D モデルは, 半導体インターフェースを使用し, コンタクトウィンドウの金属コンタクト境界条件に対して接触抵抗のオプションを有効にすることで, 簡単に設定することができます.
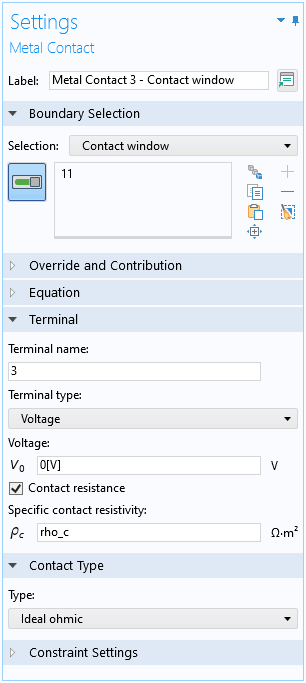
コンタクトウィンドウの接触抵抗のオプションが有効になっています.
左側の端子には, 電流入力の代わりに小さな電圧 V0 を印加し, 収束しやすくしています. 入力電流は内蔵の変数で解いた後, 簡単に評価することができます. 右側の端子では, ブリッジ電圧計のインピーダンスは無限と仮定し, 金属コンタクトにゼロ電流の境界条件を適用し, 測定された電圧降下は解いた後の端子電圧に対応します.
デフォルトの有限体積離散化で必要とされるスウェプトメッシュが使用されています. メッシュは, テスト構造の寸法をスイープしたときに, コンタクトウィンドウの周囲の解像度が維持されるようにパラメーター化されています.
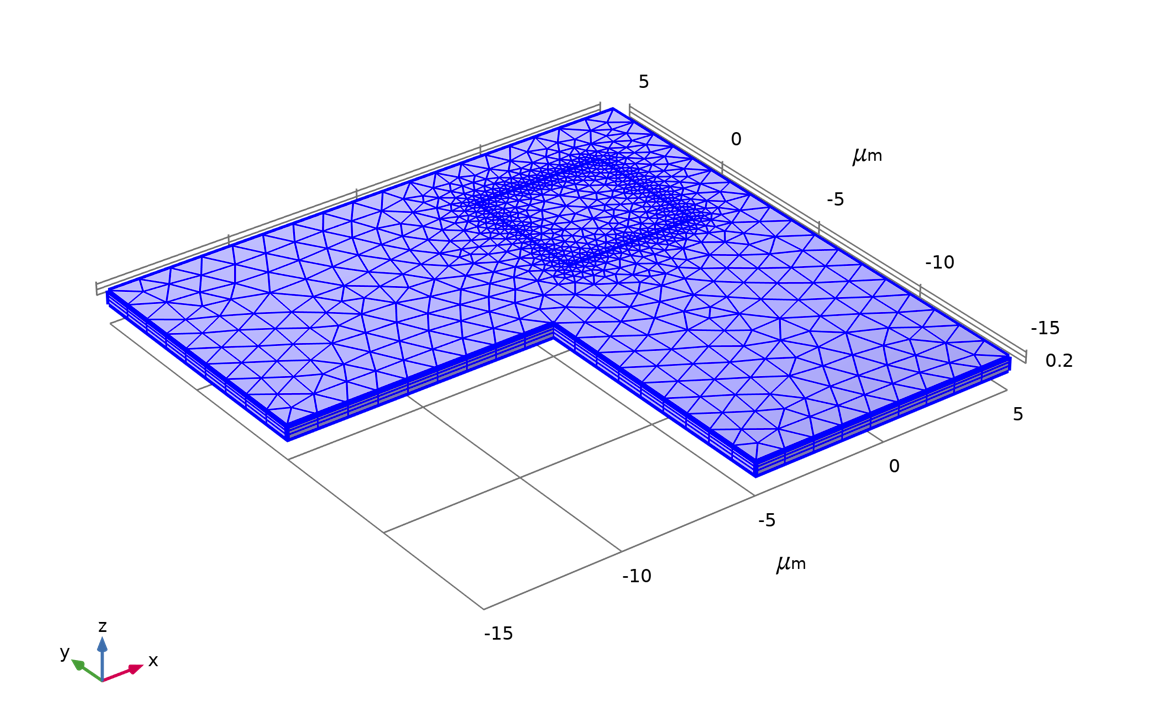
モデルで使用されているメッシュの一例.
2D モデル設定
カスタマイズされた方程式1~4を持つ 2D モデルは, 3D モデルに使用したのと同じジオメトリの上面で, 一般形式境界 PDE 数学インターフェースを使用して簡単に作成できます. この数学インターフェースは表面上に “存在” するため, “ドメイン” は 2D サーフェス, “境界” は 1D のエッジとなります. 従属変数には V2D という名前がつけられ, 方程式系中の変数 V_{2D} を表現しています.
方程式1と2の左辺は同一であり, 以下のスクリーンショットに示すように, デフォルトの一般形式 PDE のドメイン条件で実装することができます. ここでは, 保守型流束のデフォルト式からマイナス記号を削除し, ソース項と減衰係数をゼロに設定して方程式系の左辺と一致させます. (保守型流束ベクトル {V2DTx,V2DTy,V2DTz} は導電率加重平均電位 \nabla_t V_{2D} の接線方向の勾配を表します.)
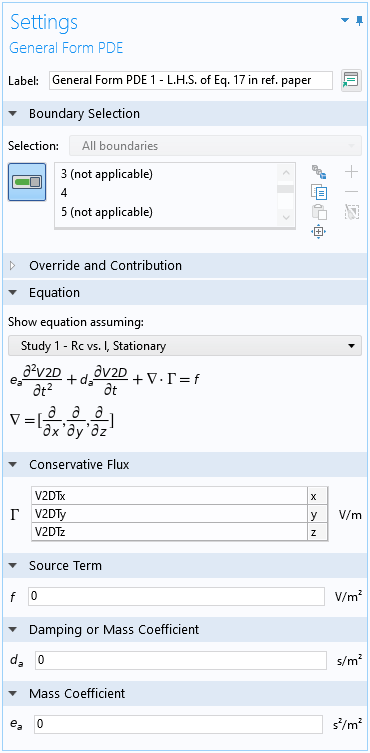
デフォルトの一般形式 PDEのドメイン条件の設定ウィンドウ.
方程式1の右辺について, 接触窓にソースのドメイン条件を追加し, ソース項の入力に右辺の式 \frac{V_{2D}}{l_t^2} に対応する式 V2D/lt^2 を入力します.
ディリクレ境界条件を使用し, 3D モデルと同じ小さな電圧 V0 を左端子に印加します. 式3に基づいて正確な電流密度を得るために, 弱拘束使用のチェックボックスを有効にします. これは, 境界上にラグランジュ乗数 V2D_lm を作成し, 求解するようにソフトウェアに指示するものです. 式3に対応する表式 V2D_lm[V/m]/Rs を使うことで, この値から法線方向の入力電流密度を計算することができます. そして, 電流密度を境界上で積分演算子を使って積分することで, 端子での総入力電流を計算することができます.
右側の端子にも弱拘束のあるディリクレ境界条件を適用し, そして未知の印加電圧 V2D_ode を指定します. グローバル方程式ノードを追加し, 端子電流がゼロになるように, 未知の V2D_ode を解きます (ブリッジ電圧計のインピーダンスが 3D モデルのように無限大であると仮定します). 端子電流は, 左側の端子と同様にラグランジュ乗数から計算されます.
最後に, コンタクトウィンドウから流出する法線方向の電流密度の式は, 式4で与えられるように, 単に V2D/rho_c となります.
スタディと結果
参考文献1で行われた2種類の実験に続き, パラメトリックスイープを用いてコンタクトウィンドウサイズ l と拡散タップ幅 w を変化させる2つのスタディが作成されます. (補助スイープでは, ジオメトリやメッシュを変化させることはできないことにご注意ください).
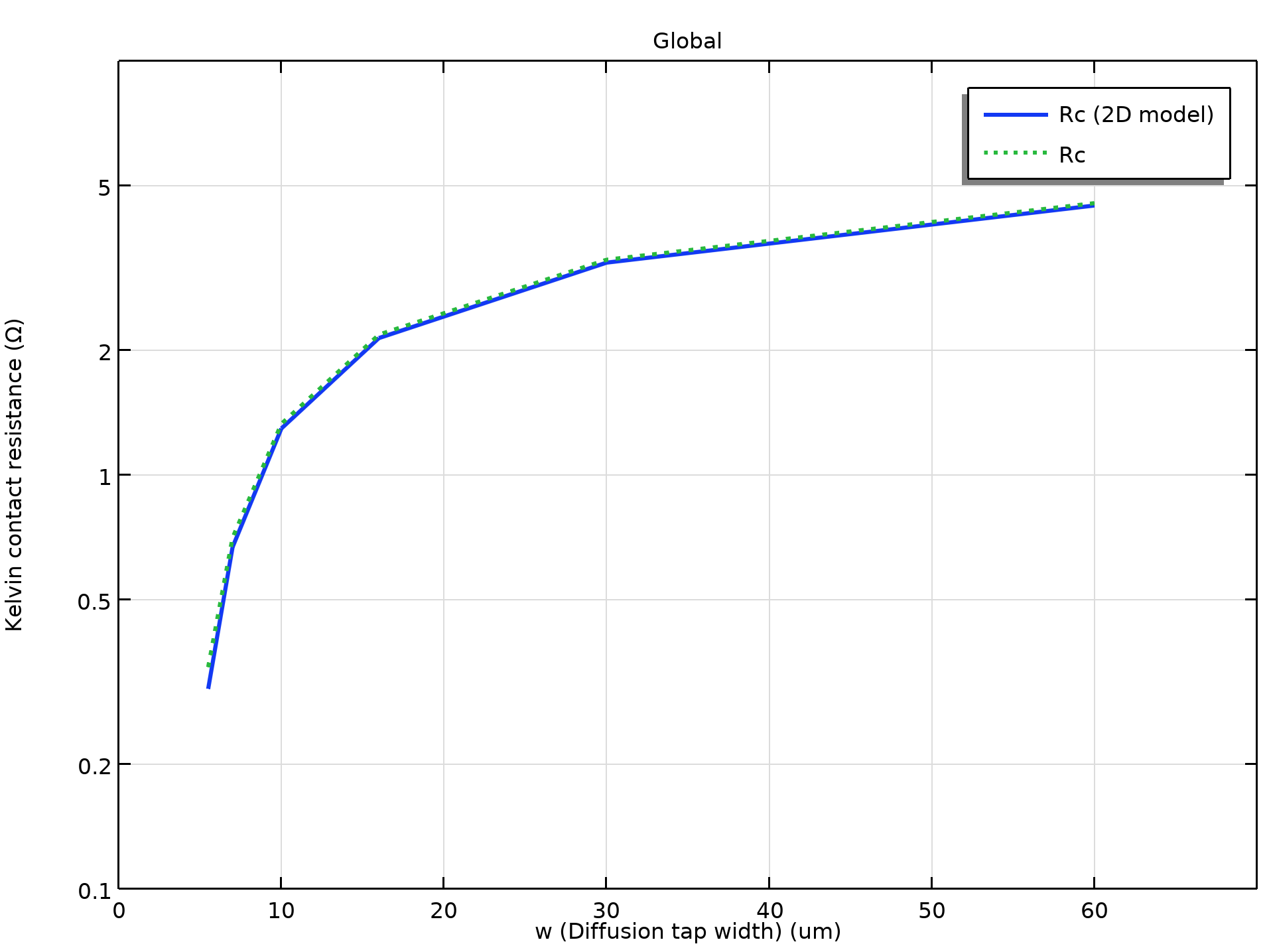
モデルへの入力として, 特性接触抵抗 \rho_c のベストフィット値 (4.5e-8 Ω cm2) を用いて, シミュレーションしたケルビン接触抵抗 R_c を, コンタクトウィンドウ面積 l^2 と拡散タップ幅 w に対してプロットすると, 次の2つのプロットのようになります.
接触面積 l^2 および拡散タップ幅 wに対するケルビン接触抵抗 R_c のシミュレーション結果. 実線カーブ: 2D モデル, 点線カーブ: 3D モデル.
2D モデルと 3D モデルで非常によく似た結果が得られ, 参考文献の図とよく一致していることがわかります.
最後に
このブログでは, 金属コンタクト境界条件に対する接触抵抗機能の使用方法をご説明しました. また, 内蔵の数学インターフェースを使用した方程式ベースのモデリングがいかに簡単であるかについてもご解説しました. 皆さんは, COMSOL Multiphysics のこの柔軟性と汎用性をどのようにシミュレーションに活用しているか, ぜひ下のコメント欄でお聞かせください!
試してみましょう
以下のボタンをクリックすると, アプリケーションギャラリと MPH ファイルをダウンロードしていただけます. 特性接触抵抗を抽出するためのクロスブリッジケルビン抵抗器のモデリングをぜひお試しください.
参考文献
- W. M. Loh, S. E. Swirhun, E. Crabbe, K. Saraswat and R. M. Swanson, “An accurate method to extract specific contact resistivity using cross-bridge Kelvin resistors”, IEEE Electron Device Letters, vol. 6, no. 9, pp. 441–443, 1985, doi: 10.1109/ EDL.1985.26185.
- W. M. Loh, S. E. Swirhun, T. A. Schreyer, R. M. Swanson and K. C. Saraswat, “Modeling and measurement of contact resistances”, IEEE Transactions on Electron Devices, vol. 34, no. 3, pp. 512–524, 1987, doi: 10.1109/T-ED.1987.22957.







コメント (0)