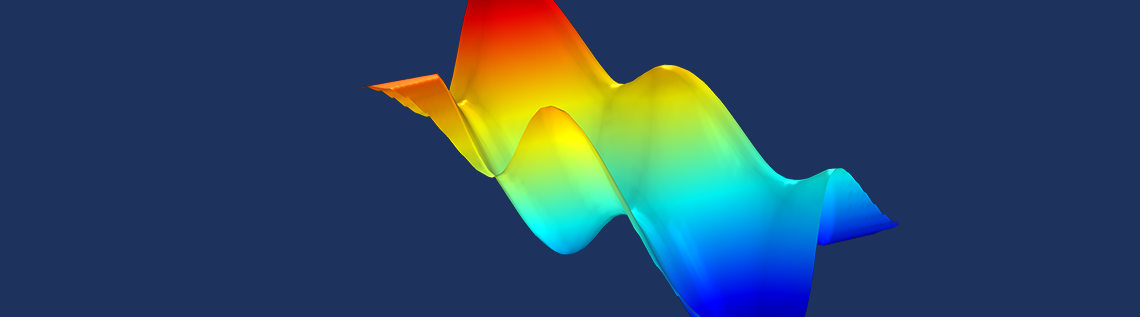
すべての解析プロジェクトが, CADモデルから始まるわけではありません. 時には, 利用可能なデータが点の集合(点群とも呼ばれる)しかない場合があります. このブログでは, 点群データを COMSOL Multiphysics® ソフトウェアでのシミュレーションに使用できるジオメトリモデルに変換する方法をご紹介します.
点群とは?
点群とは, X, Y, Z座標で表される3次元の点の集合のことです. 点は通常, レーザー, 測定機器, レーダーなどを使ってスキャンされた物理的な物体の表面から得られます.
下のスクリーンショットは, 「Notepad」のテキストファイルで, x-, y-, z– 座標がタブで区切られた列に整理された点群データファイルの先頭を示しています.
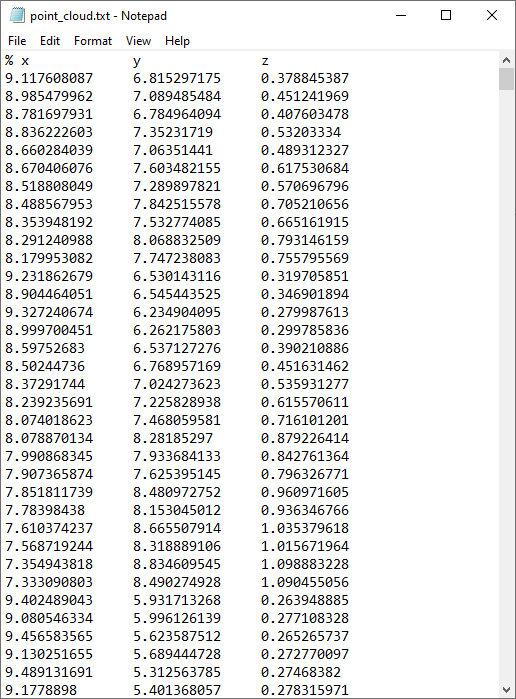
点群データのテキストファイル.
これは, COMSOL Multiphysics がインポートできる座標フォーマットの中で最もシンプルなタイプの一つです. スプレッドシート形式と呼ばれます. このフォーマットでは, コメント行を示すために任意の%(パーセント) 文字を使用することができます. 値とインデックスは, スペース, コンマ, セミコロン, タブのいずれかの文字で区切ることができます.
インポートされた点は, その座標のファイルの行番号に応じてインデックスが割り当てられます. このようなポイントセットには, ポイント間の関係(接続性)に関する情報がないため, 曖昧さが生じることがあります. どのような曖昧さが発生するか, 簡単な2Dの例を見てみましょう. 下の図のような2次元の曲線の場合について考えてみます. この図から, 点5, 18, 7が曲線上の連続した点であることは明らかです.
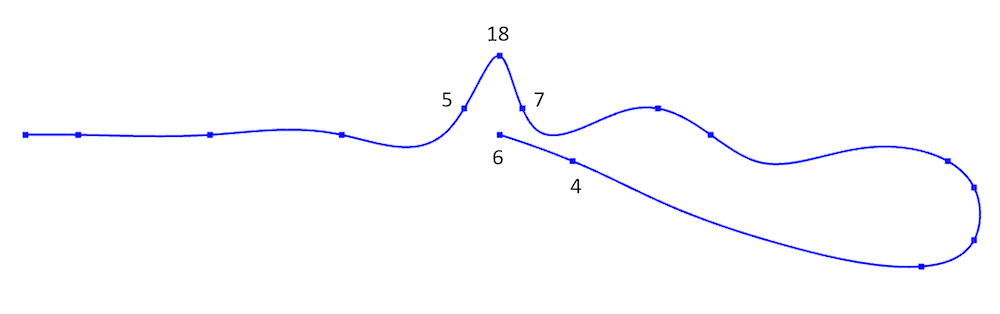
しかし, 点群データを取り込んだ曲線に対応する次の図では, あまりわかりません. 5, 6, 4は曲線上の連続した点かもしれません.
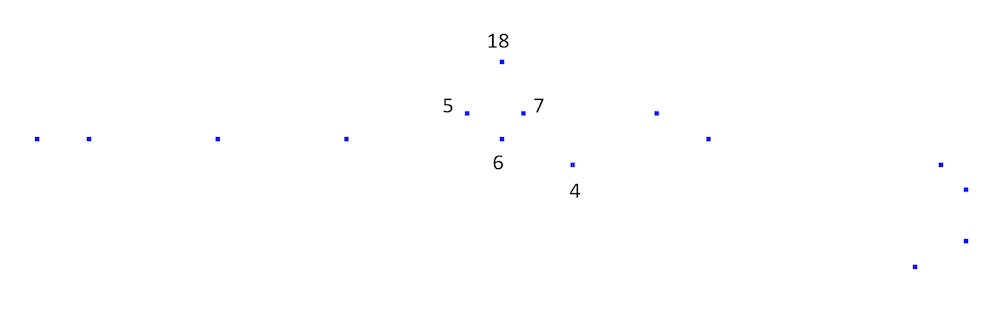
点群データには本質的な曖昧さがある場合があります. 点5, 6, 4はつながっているのでしょうか? この場合, これらの点はつながっていません. これは, 元の曲線からはわかりますが, 比較的疎らにサンプリングされた点群からはわかりません.
STL, PLY, 3MFなどのファイルフォーマットのように, インポートされた3D座標のリストに, 関連する三角形の曲面接続性データが含まれている場合, この曖昧さは解消されます. これにより, 点間の接続性によって定義された三角形のリストが得られ, これによって曲面が一意に定義されます. 例えば, 曲面三角形のデータファイルでは, 以下のような行は,
15 17 23
インデックス15, 17, 23の点が三角形の頂点として接続されていることを意味します.
一方で, 接続性の情報がない点群データしかない場合, このような曖昧さを解消するためには, 追加の仮定が必要になります. 例えば, 曲面データがz=f(x,y)の形をしていると仮定するとします. もし, データがそのような形でない場合は, z=f(x,y)という形でいくつかのパーツに分けてみることができます. なお, y=f(x,z)やx=f(y,z)といった形式のデータでも, いくつかの工夫をすれば同じように使用できます.
点群の可視化
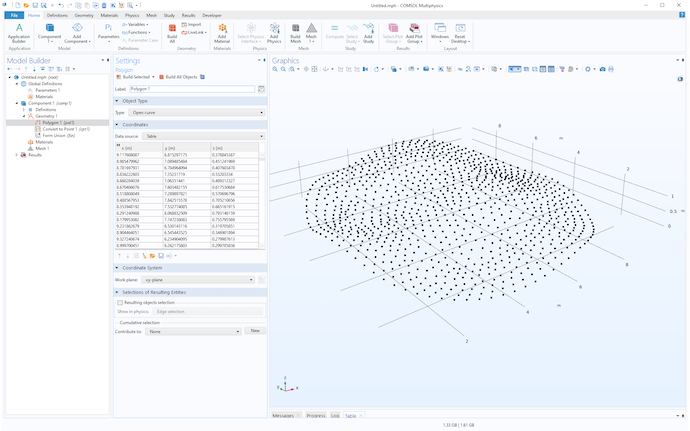
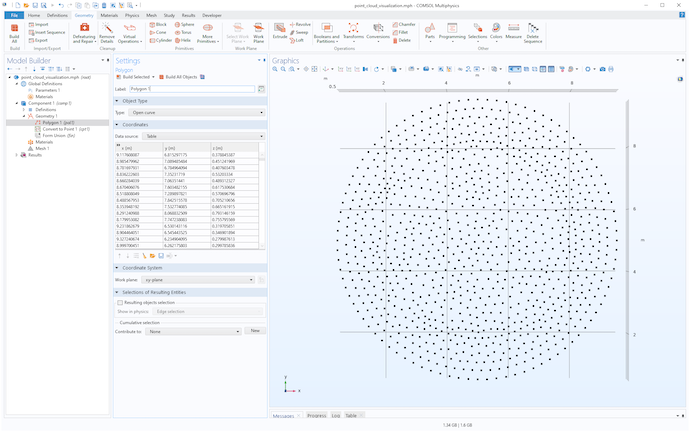
点座標データを簡単に可視化する方法として, 下図のように多角形ジオメトリオブジェクトにテーブルとしてインポートし, 点群に変換操作を行う方法があります.
点群データを2つの異なる角度から見たジオメトリ点群オブジェクトとして可視化したもの.
この可視化結果から, 点群はz=f(x,y)という形の関数曲面を定義していると考えられます. 後で使用するためには, 点群の範囲を知る必要があります. この情報を簡単に得るには, ジオメトリノードを右クリックして測定を選択します.
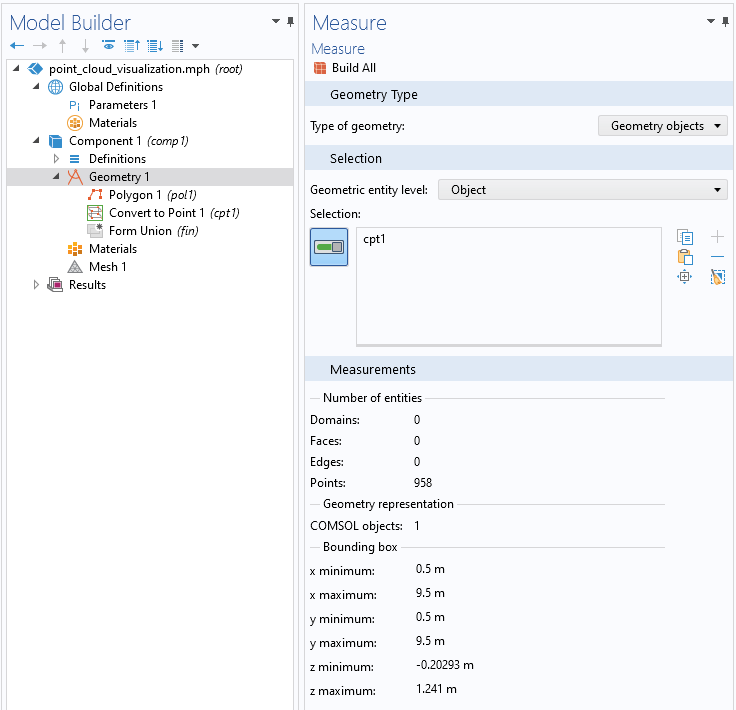
測定設定ウィンドウでは, 点群の範囲に関する情報を得ることができます.
x方向, y方向ともに0.5から9.5まで, z方向は約-0.2から+1.5mまでの958個の点があることがわかります. この例では, 単位をメートル(m)としています.
ここで, 曲面に変換という操作を使って, この点群を曲面に変換しようとします. しかし, これはうまくいきません. 点の接続性情報がないため, エラーメッセージが表示されます. 接続性データを何らかの方法で構築する必要があります. さらに, データがz=f(x,y)の形であるという仮定を使用する必要があります. 解決策としては, 点群を構造化されていない補間曲面としてインポートすることです.
補間曲面の作成
次のステップとして, グローバル定義に補間機能を追加し, データソースをファイルに設定します. 下図のように, 点群のテキストファイル(この例では, C:\COMSOL\point_cloud.txt)を参照します. このファイルは, このブログの最後にあるリンクからダウンロードできます.
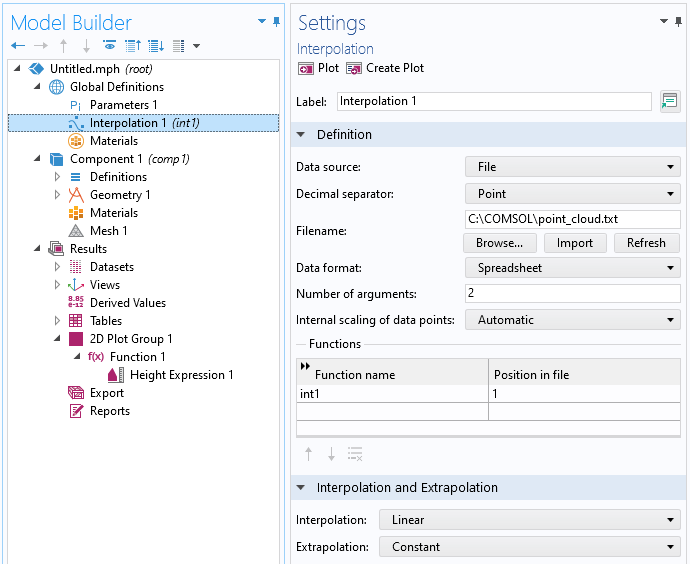
点群によって定義された補間関数.
補間機能は, データがz=f(x,y)フォーム上にあり, ファイルの最初の2列がそれぞれx-座標とy-座標を表し, 3列目が関数値を表していることを自動的に推測します. 私たちは, これを関数曲面のz-座標と解釈します. これは, 引数の数が自動的に2に設定されていることからもわかります(x-座標とy-座標にそれぞれ対応しています). 関数名は自動的にint1に設定され(変更可能), ファイル内の位置の設定1は, z-座標を表すint1(x,y)の関数値が, 入力引数の列に続く最初の列で与えられることを意味します. つまり, 列番号2+1=3となります. この場合, ファイルには3列しかないので, 1だとわかります. データの形式が異なる場合は, テキストエディターや Excel® などの表計算ソフトを使って, データを並べ替えてから読み込むことができます.
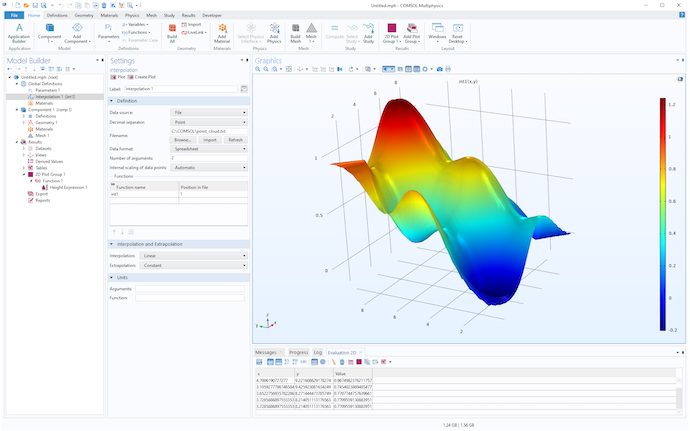
補間設定ウィンドウの上部にあるプロットまたはプロットの作成ボタンをクリックして, 補間関数を可視化します. プロットオプションは一時的な可視化を行い, プロットの作成は2Dグリッドデータセットとそれに関連する関数のプロットを結果の下の2Dプロットグループに作成します.
補間関数が可視化され, 結果とそれに関連する設定ウィンドウの下に関数プロットとして表示されたもの.
z=f(x,y)という仮定だけで, ソフトウェアはどのようにしてこの曲面表現を作ったのでしょうか? 補間機能は, 裏でx-座標とy-座標の2次元三角メッシュを作成し, 各点に関数値を関連付け, 最後に関数値間の線形補間を行います. これは, 点群の上に魚網を落としたようなものだと考えることができます. なお, この三角メッシュはユーザーには見えません. 補間と外挿セクションの補間の設定ウィンドウで, 補間の設定を見ることができますが, デフォルトでは線形に設定されています. もう一つのオプションはニアレストネーバーですが, これは断片的な定数関数の補間を行うもので, ここでは役に立ちません.
このセクションのもう1つの設定は外挿です. これは,関数の定義領域(x-座標とy-座標で決まる)の外側にある関数の値を推測するために使用します. この場合, 点群はxy平面上の円内に分布しています. データを関数プロットとして可視化する場合, xyデータは長方形のグリッド2Dデータセットから取得され, 補間機能によって一定の関数値が放射状に割り当てられ, 点群データを囲む円と長方形の間のスペースを埋めます. これは下の図で確認することができ, 点群データから円形のインプリントを識別することもできます.
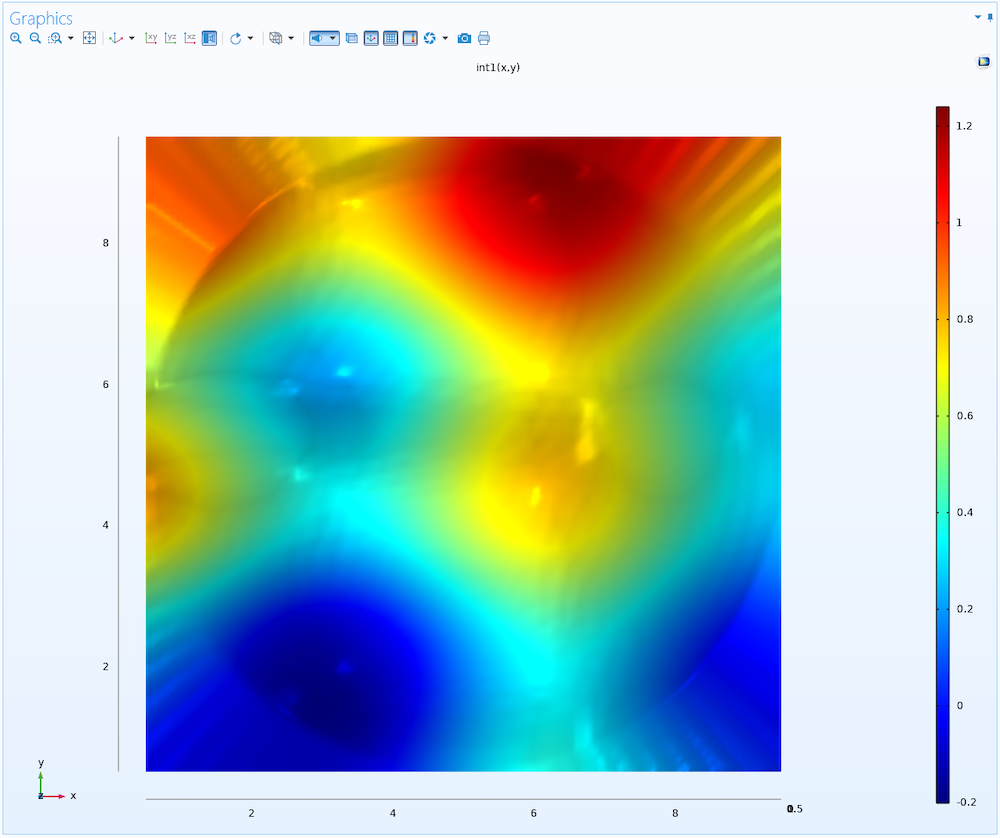
補間機能を上から見た図. 元の点群のフットプリントを定義する円形の領域の外側に, 外挿された部分が見えています.
この補間関数を, メッシングやシミュレーションに使用できるジオメトリ表現に変換するにはどうすればよいのでしょうか. これには, 次に説明するように, パラメトリック曲面ジオメトリオブジェクトを使用します.
パラメトリック曲面の作成
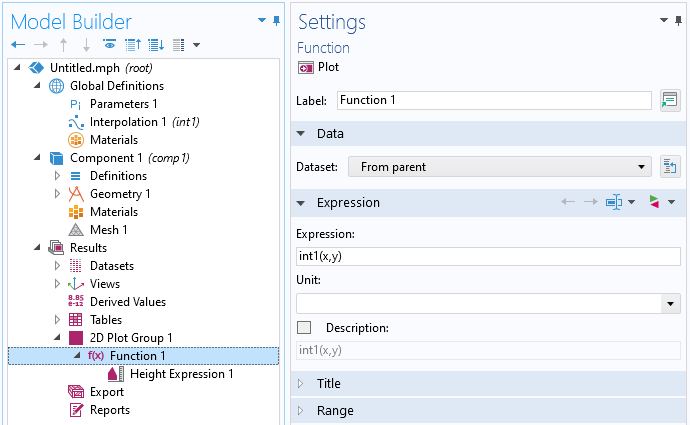
上記の補間機能に従うジオメトリ曲面を作成するには, 下図のようにジオメトリの下にパラメトリック曲面機能を追加します.
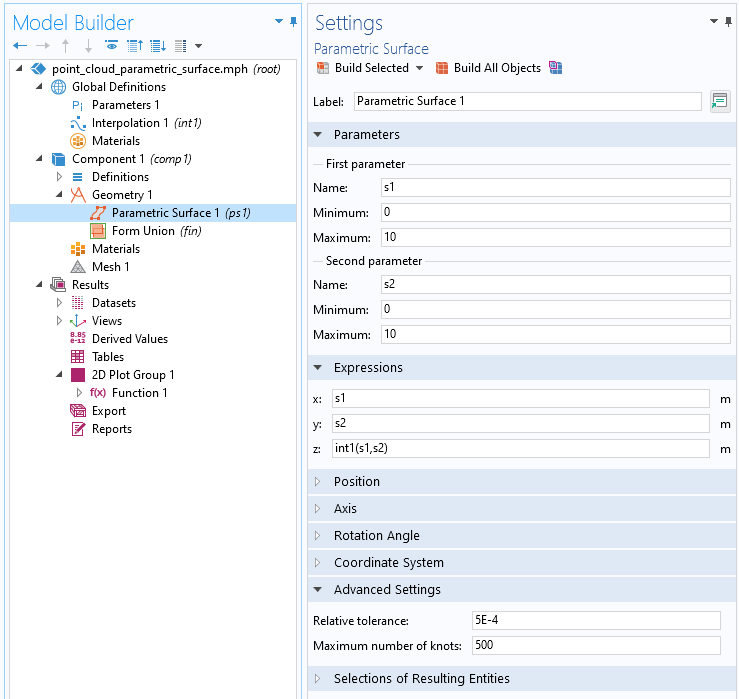
点群補間機能に基づいた曲面のパラメトリックサーフェス設定.
この設定画面では, s1とs2をそれぞれx-座標, y-座標とし, int1(s1,s2)をz-座標と解釈しています. ここで, 先ほど測定ツールで得た情報を使います. s1とs2の最小値と最大値は, 点群の測定範囲よりも少し広く設定して, 細部を見逃さないようにします.
この場合, パラメトリックサーフェスは両方向とも0~10の間で定義され, 0.5~9.5の間で測定された点群データと比較されます.
内部的には,パラメトリックサーフェスをBスプラインサーフェスで表現しており, れはx-,y-,z-の式で定義される数学的な曲面を近似するように計算されています. Bスプラインサーフェスは区分多項式曲面で, 使用される区分多項式の数はノットの数によって間接的に決定されます. ノットの数が多いほど, 区分多項式の数が増え, より良い近似が可能になりますが, 計算コストは高くなります. Bスプラインサーフェスのノット数は, 表面近似が相対的な許容範囲フィールドで指定された許容範囲を満たすまで, または最大ノット数フィールドで指定されたノット数に達するまで, 自動的に増加します. 許容値は, パラメトリックサーフェスのバウンディングボックスの空間対角線を基準にして測定されます.
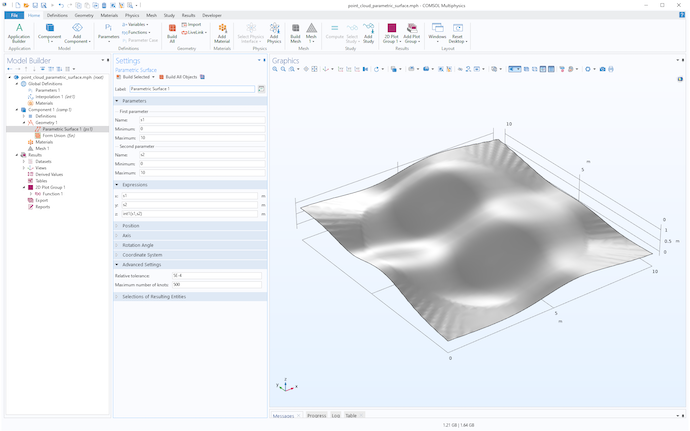
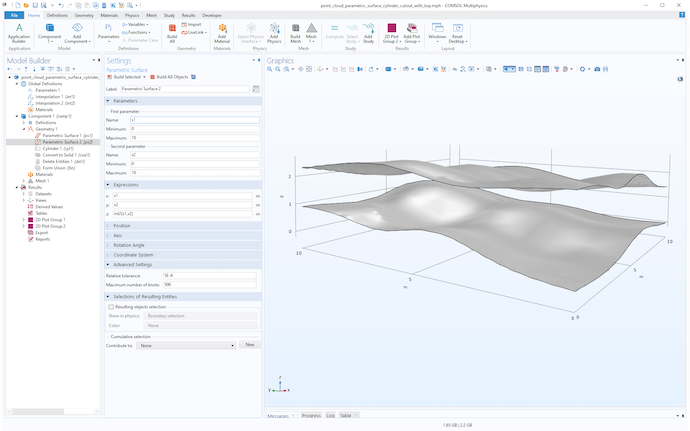
ここでは, 試行錯誤の結果, 相対的な許容範囲を5e-4, 最大のノット数を500としました. (デフォルトはそれぞれ1e-5と20) その結果, 表面は次の図のようになりました.
パラメトリックサーフェスジオメトリオブジェクト.
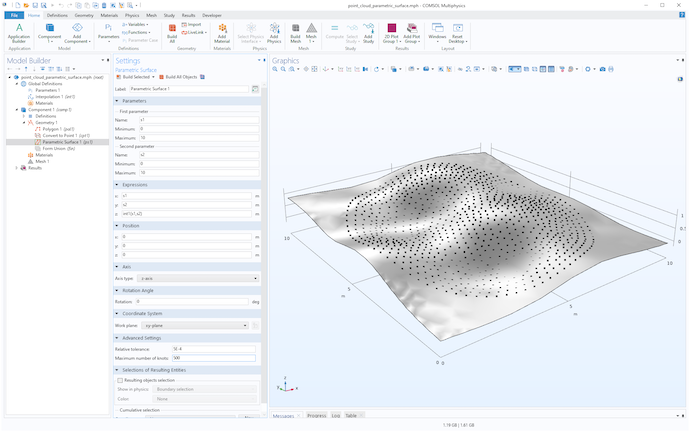
先ほどの方法を使って, 下の図のように点群とサーフェスを同時に可視化することができます.
パラメトリック曲面ジオメトリオブジェクトと点群.
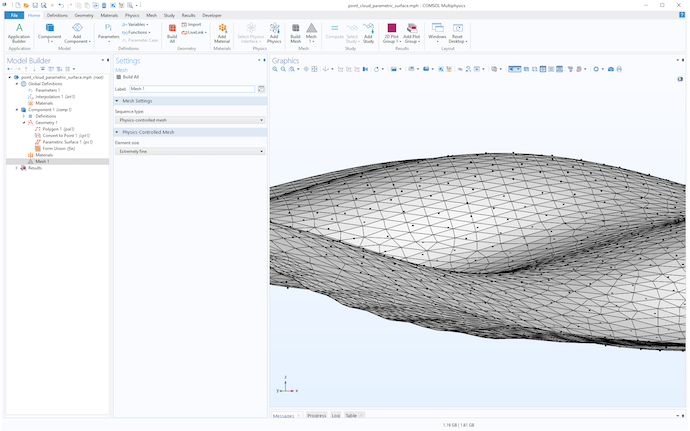
表面可視化の詳細度をより制御するには, メッシュノードをクリックして, 適切な要素サイズのメッシュを作成することができます. 次の図は, 非常に細かい設定のメッシュを示しています. さらに高い解像度を得るには, ユーザーが制御するメッシュオプションを選択し, カスタム要素サイズを設定します.
点群とパラメトリックサーフェスジオメトリをメッシュで可視化したもの.
サーフェスのトリミング
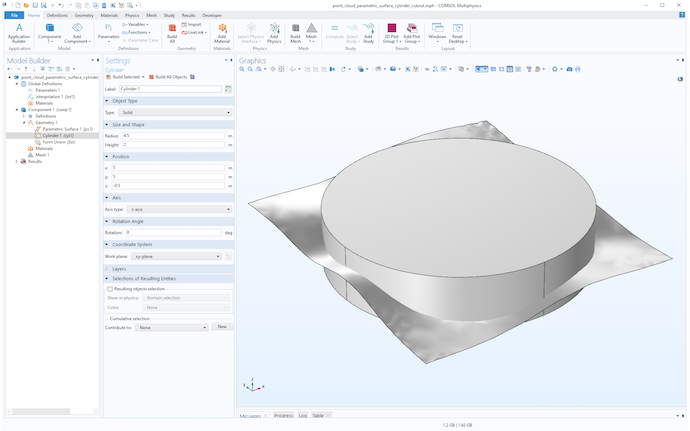
元の点群データは, x = 5, y = 5を中心とした半径4.5の円形のフットプリントを持っています. 次の図は, これらの測定値にフィットし,z方向の最小値と最大値に従う高さを持つ円柱を追加した結果です.
サーフェスのトリムに使われた円柱.
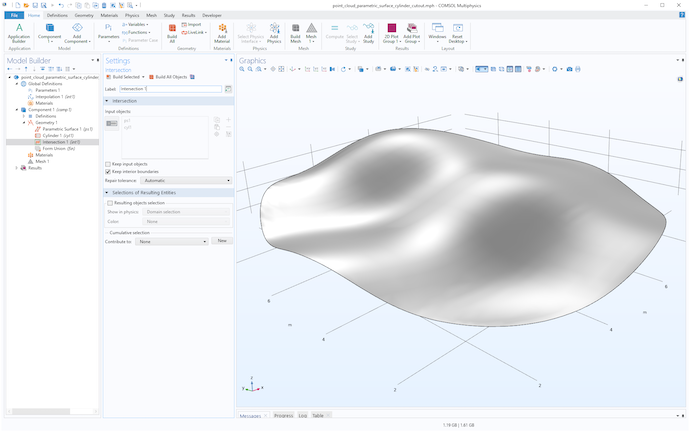
次に, 下図のように, サーフェスと円柱の両方を選択して, 交差操作でサーフェスをトリミングします.
サーフェスと円柱を交差させた結果.
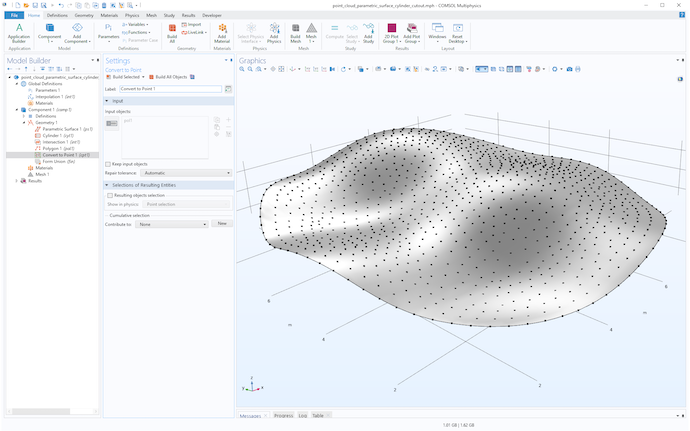
点群とトリムされた曲面.
2つの曲面間のスペースでのソリッドの作成
2つの補間されたサーフェス間のスペースに円形のフットプリントを持つソリッドを作成するには, 次の図のように, 上記の手順を繰り返して2つ目のサーフェスをインポートします.
2つ目の点群に対応する2つ目のサーフェス.
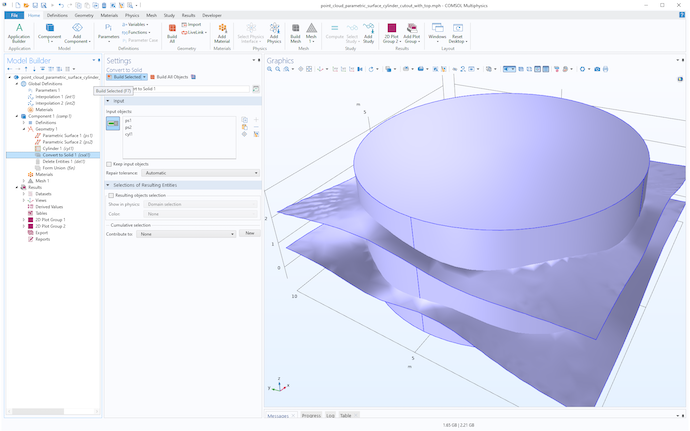
次に, サーフェスをトリミングするためのシリンダーを作成し, 次の図に示すように, すべてのオブジェクトに対してソリッドに変換操作を行います.
円柱を使って2つのサーフェスをトリム.
オブジェクトの分割またはドメインの分割のいずれかの操作を使用することでも同じ結果を得ることができます. これらの操作はソリッドに変換よりも洗練されており, 分割するオブジェクトまたはドメインとして円柱を選択することができます. 次に, 分割に使用するツールオブジェクトとして補間サーフェスを選択します. ドメインの分割では, オブジェクトから選択したドメインを分割することができ, 分割するドメインと交差していない平面, 円筒, 球体のツール面を自動的に拡張するオプションもあるので, 状況によってはより汎用的な操作が可能です.
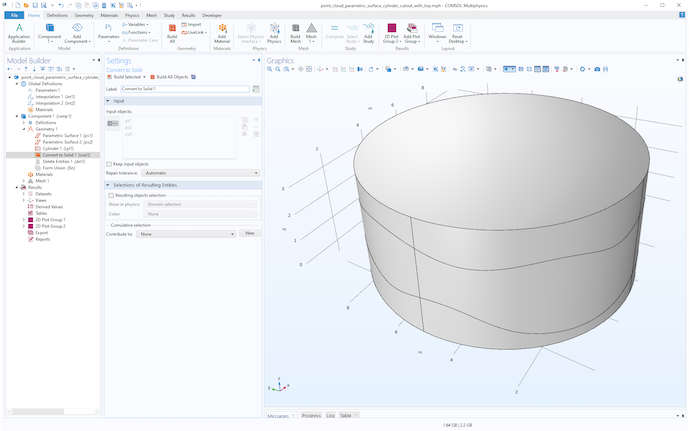
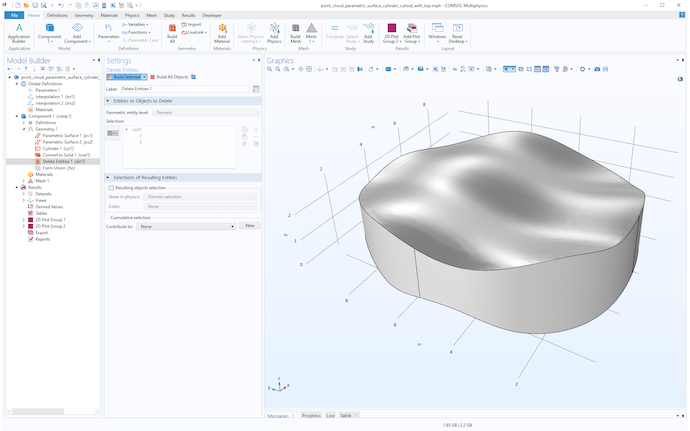
最後にエンティティの削除で不要なドメインを削除すると, 下図のようになります.
2つの補間サーフェスをインポートしてトリミングしたソリッド.
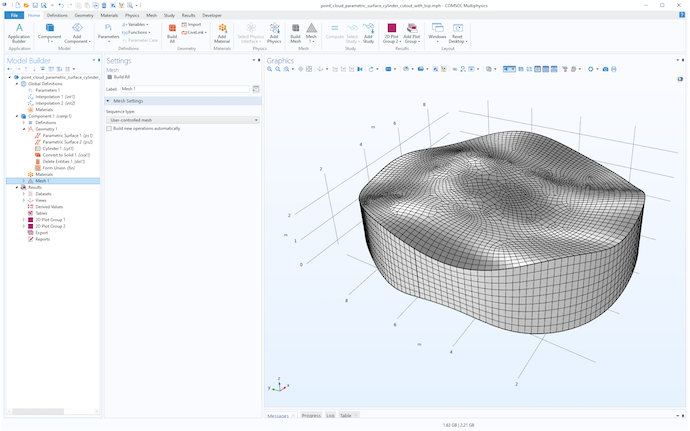
これで, このソリッドをメッシュ化して, あらゆるタイプのシミュレーションに使用することができます. ここでは, 次の図のように, スイープヘックスのみのメッシュを作成します.
円筒形ソリッドのスイープメッシュ.
テスト用点群データの作成
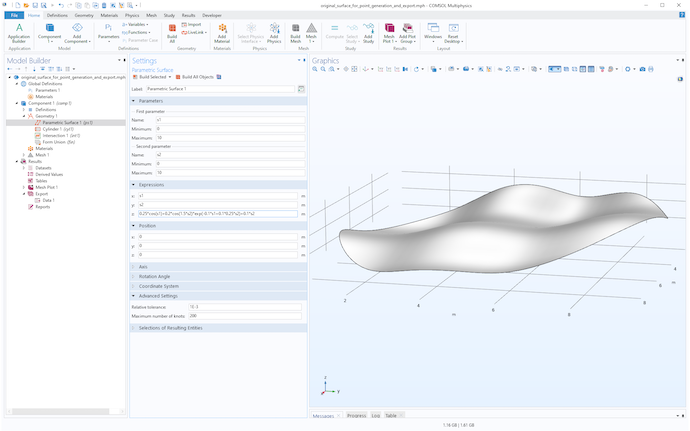
今回のブログで使用した点群データとファイルは, このページの下にあるリンクからダウンロードしていただけます. ご自分で点群データを作成したい場合は, 任意の曲面から始めることができます. 次の図では, 上の例と同じように円柱で縁取られたパラメトリックサーフェスを使用しており, z-座標には次のような式を使用しています.
z=0.25*cos(s1)+0.2*cos(1.5*s2)*exp(-0.1*s1+0.1*0.25*s2)+0.1*s2
実は, これは最初の例で点群データを生成した際に使用したサーフェスなのです.
数式で与えられたパラメトリックサーフェスを, 円柱オブジェクトでトリミングしたもの.
ここで, メッシュを作成し, メッシュノードを右クリックしてプロットを選択すると, 結果の下にメッシュプロットが生成されます. 次に, メッシュプロット>メッシュを右クリックし, エクスポートするプロットデータを追加を選択します. データの設定ウィンドウで, 1を式としてを使用します. このエクスポートされた定数値は使用されません. ファイル名を選択し, ウィンドウ上部のエクスポートをクリックすると, データがファイルに書き込まれます.
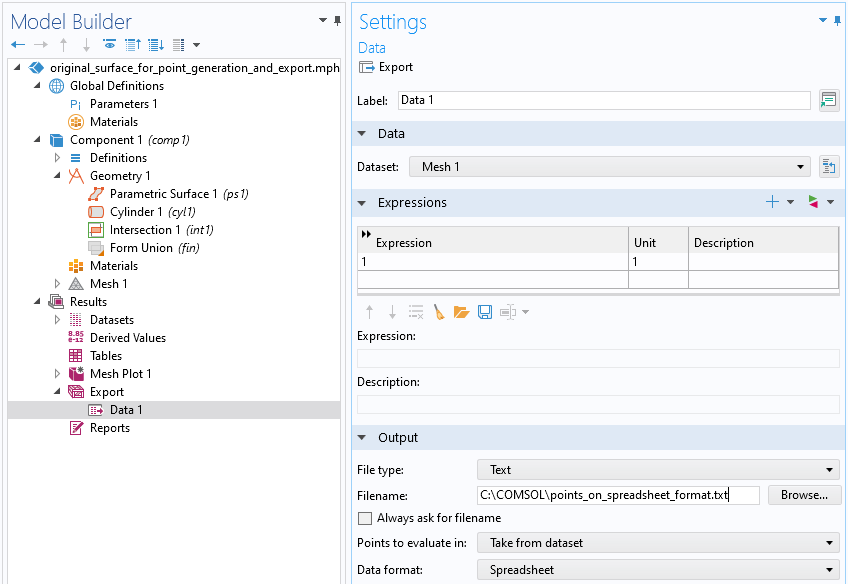
スプレッドシート形式のデータをエクスポートする際に使用されるエクスポートの設定.
できあがったテキストファイルをテキストエディターや表計算ソフトで開くと, コメント行のあるヘッダーと4つの列が表示されます. 最後の列には, 定数式1が入っています.
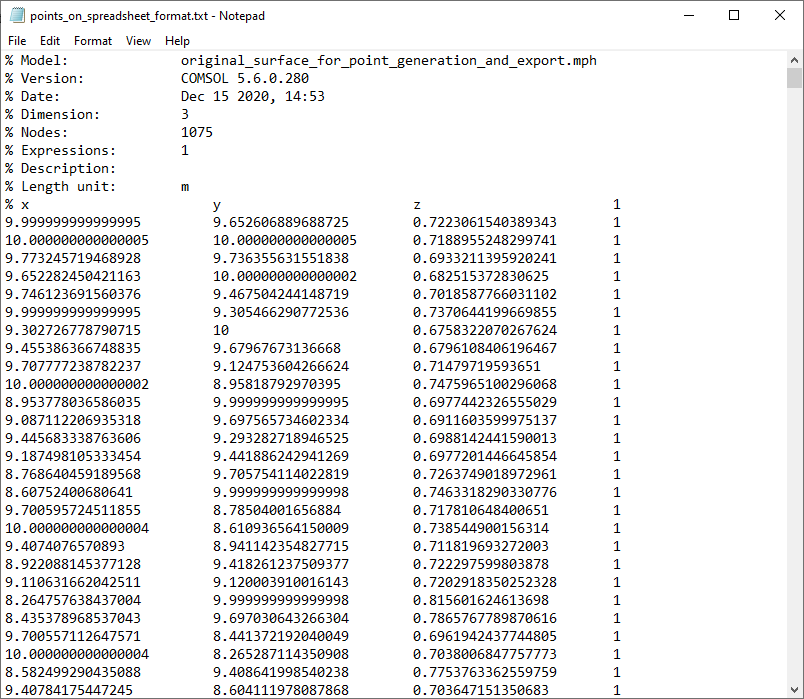
Excel® などの表計算ソフトでは, 4列目を削除して, 再度テキストファイル形式で保存することができます. できあがったファイルは, 上述の例と同じ形式になります. なお, ヘッダーの先頭のコメント行は任意であり, 削除することも可能です.
一般化と参考文献
上記のテクニックは, さまざまな方法で一般化することができます. 例えば, 2つ以上のサーフェスをインポートして, より複雑な構造を作成することができます. 円柱ではないオブジェクトを使ってデータをトリミングすることもできます. また, 点群データが円筒座標や球座標に基づいている場合もあります. 上記のテクニックと座標変換を組み合わせて, 円筒形や球形のパッチを生成することができます.
補間されたデータを地学応用で使用した実例については, こちらのブログをご覧ください. 地域スケールの地下水モデルへの地質構造の統合
さらに関連する例として, こちらのブログをご参照ください. 標高データからジオメトリを構築し, 不規則なジオメトリをモデル化する方法
試してみましょう: 点群データの変換
下のボタンをクリックすると, このブログで使用したMPHファイルとデータファイルをダウンロードできます. また, 式で定義された初期ののパラメトリックサーフェスと, 点群で定義されたパラメトリックサーフェスを比較する方法を示すMPH ファイルもご用意しています.
Microsoft および Excelは, 米国 Microsoft Corporation の米国およびその他の国における登録商標または商標です.





コメント (0)