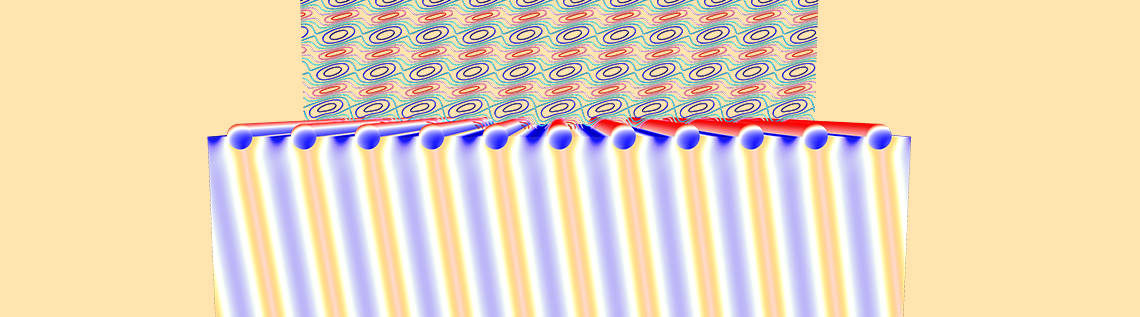
ガラスなどの誘電体に光が当たると, 光の一部は透過し, 一部は反射します. 金などの金属コーティングを施すことで, 透過率と反射率が変化し, 光の吸収も生じます. 誘電体表面と金属コーティングは, 高さや厚さにランダムなばらつきを持つことがよくあります. このブログでは, このような状況に対応する計算モデルを紹介し, 開発していきます.
シンプルなものから: 光学的に平坦な表面
粗い表面を扱う前に, まずはシンプルなものから始めましょう. 下の図に示すように, 光学的に平坦 なガラスの上に, 薄く均一な金コーティングを施したものです. このようなモデルでは, ガラス面内の構造変化はごくわずかです. さらに, COMSOL Multiphysics® ソフトウェアでは, 波長よりもはるかに小さな幅を持つ小さな2次元単位セルを想定することで, 非常に簡単にモデル化できます.
この計算モデルは, アプリケーションギャラリの検証モデルの一つである フレネル方程式の例 に基づいていますが, 波長に依存する屈折率を持つ金層を追加するように修正されています. この屈折率では, 以前のブログ で説明したように, 各材料の最小波長と表皮深さに基づいてメッシュサイズを手動で調整する必要があります.
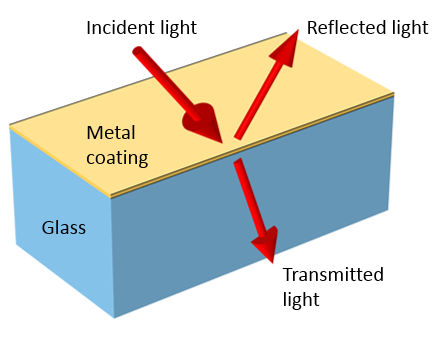
ガラス基板上の金属コーティングに入射する光は, 反射, 透過, 吸収されます.
このモデルには, モデリング領域の左右にフロケ周期境界条件, 上下にポート境界条件が設定されています. 上部のポート境界条件は, 指定された入射角で平面波を入射し, 反射光を計算します. 一方, 下部のポート境界条件は透過光を計算します. 金属層内の 損失を積分 することで, 金層内の吸光度を計算できます.
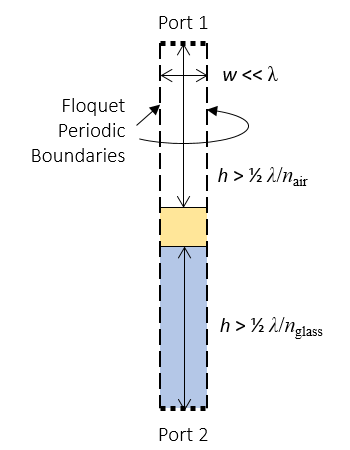
ガラス上の金属膜の光学特性を計算する計算モデル.
入射光を法線から外れた角度で計算する場合, モデリング領域の高さ, つまり物質界面とポート境界条件間の距離にも注意を払う必要があります. この距離は, モデリング領域内でエバネッセント場がほぼゼロに減衰するほど十分に大きくなければなりません.
その理由は, ポート境界条件が電磁場の伝搬成分のみを考慮できることに関係しています. ポート境界条件に到達する電磁場のエバネッセント成分は人工的に反射されるため, ポート境界を物質界面から十分に離れた位置に配置する必要があります. 多くの場合, エバネッセント場がどこまで広がるかを判断するのは困難です. 簡単な目安としては, ポート境界条件を物質界面から少なくとも半波長離して配置し, 領域を拡大することで結果が変化するかどうかを確認します.
以下のサンプル結果は, 透過光, 反射光, 吸収光, およびそれらの合計を示しています. これらの合計は常に1になるはずです. 合計が1にならない場合は, モデルの設定を慎重に確認する必要があります.
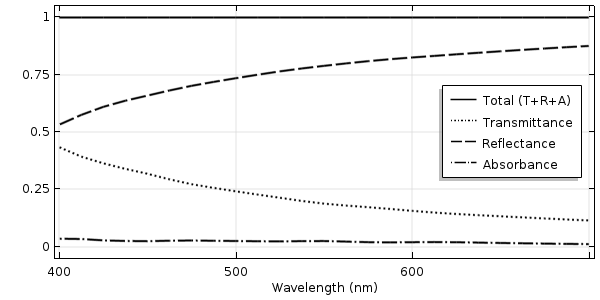
金属コーティングを施した平坦なガラス面に垂直に入射する光の透過率, 反射率, 吸光率を波長の関数として表したものです.
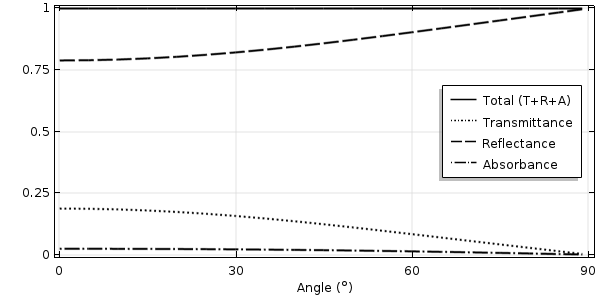
様々な入射角における 550 nm 光の透過率, 反射率, 吸光率.
複雑さの付加: 周期的な変化を持つ表面
ここで, もう少し複雑な例として, 周期的な構造変化. すなわち正弦波状のリップルを導入してみましょう. 当然のことながら, 単一のリップルを考慮した, より大きな単位セルを考慮する必要があります.
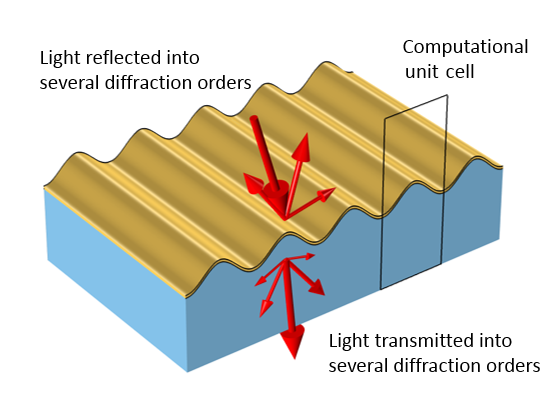
周期的な変化を持つ表面は, 複数の異なる回折次数の光を反射および透過します.
これまでと同じ主要特性と境界条件をすべて適用できます. しかし, 間隔が十分に大きい場合, 高次の回折が発生する可能性があります. つまり, 光は複数の異なる方向に反射および透過する可能性があります. 反射と透過を適切に計算するには, 複数の回折次数ポートを追加する必要があります. ソフトウェアは, ドメイン幅, 材料特性, および指定された入射角に基づいて適切なポート数を計算します. 入射角の範囲を調べる場合は, 角度スイープの限界に存在するすべての回折次数を計算する必要があります.
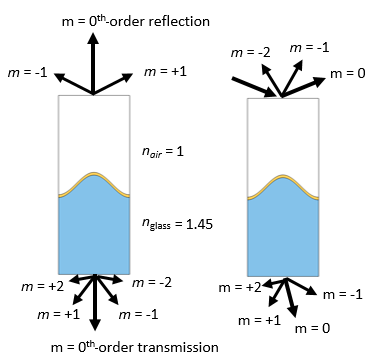
波長とドメイン幅の比, 屈折率, および入射角に応じて, 複数の回折次数が存在する可能性があります.
高次回折が現れる条件と適切なモデリング手順については, プラズモニックワイヤーグレーティング の例で詳しく説明しているので, ここでは長々と説明しません. つまり, 上下の材料の波長に対して計算領域が広いほど, より多くの回折次数が存在する可能性があります (回折次数の数は入射角によって異なります). 以下に示す結果は, 総透過率と反射率をプロットしたものです. つまり, 異なる回折次数で反射された光と透過光がすべて合計されています.
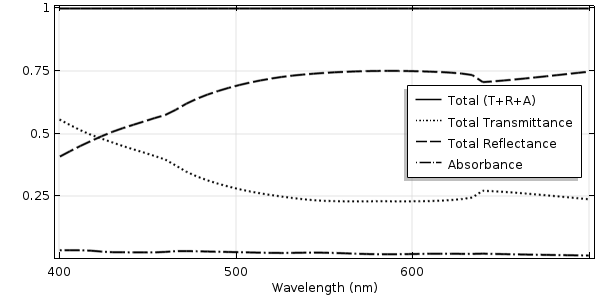
金属コーティングされた波状ガラス表面に垂直に入射した光の透過率, 反射率, および吸光率.
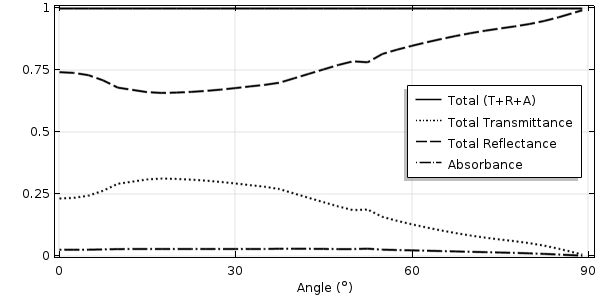
様々な入射角における 550 nm 光の透過率, 反射率, および吸光率.
より困難なケースの求解: ランダムな粗さを持つ表面
では, 計算上最も難しいケース, すなわち表面の高さに多くのランダムな変化がある表面に移りましょう. このランダム性をモデル化するには, 幅が徐々に増加する複数の異なる領域と, 粗面プロファイルの異なるサブセットをモデル化する必要があります. 領域幅が広くなるにつれて, そして表面の異なるサブセットがサンプリングされるにつれて, これらの異なるモデルから計算される平均的な挙動は収束します. つまり, 粗面をサンプリングすることで一連の統計値を生成します. これらの統計値の計算方法を詳しく説明するのではなく, ここで説明するように, 高さの変化をランダムな高さと位相を持つ異なる正弦波の合計として定義することにより, 粗面を近似する1つの領域をモデル化する方法に焦点を当てましょう.
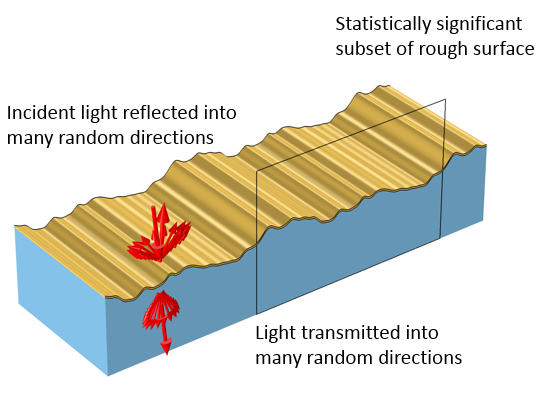
ランダムな変化を持つ粗面は, 光をランダムな方向に反射および透過します. 計算モデルは, 粗面プロファイルの統計的に有意なサブセットをサンプリングする必要があります.
計算領域は非常に広く, 波長の数倍の長さにする必要があります. 構造物に様々な角度で入射する平面波をモデル化したいため, フロケ周期境界条件を使用します. この条件では, 周期境界上に同一のメッシュが必要です. 実際には, 左側と右側の境界が同一になるように, 領域の形状を若干変更する必要があるかもしれません. ここで説明したように, 正弦関数の和を使用すれば, プロファイルは自動的に周期的になります.
ポート境界条件を用いて波を発射したいのですが, 反射光と透過光をモニタリングするために回折次数ポートを使用することはもはや現実的ではありません. なぜなら, 数百 (あるいは数千) もの回折次数が生じる可能性があるからです. さらに, このモデルは統計的なサンプリングを表すため, これらの異なる次数に散乱された光の相対的な割合は重要ではなく, 反射光と透過光の合計のみに着目します. つまり, このモデリング手法は, 積分散乱光の総和に加え, 表面の鏡面反射と透過を計算します.
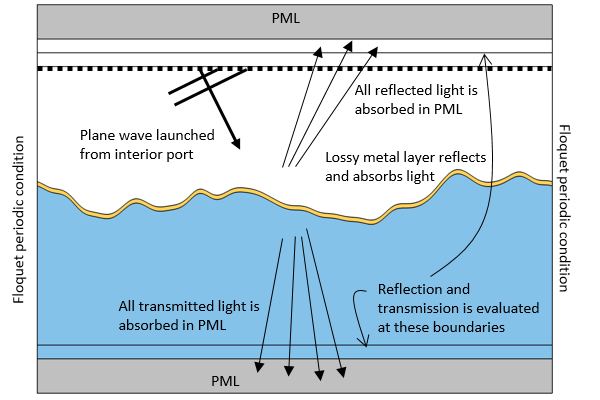
粗面モデルの計算領域. 光は内部ポートから物質界面に向けて発射されます. このポートに向かって反射された光はポートを通過し, 透過光と同様に PML に吸収されます. 全反射率と透過率をモニタリングするために, 2つの追加境界が導入されます.
そこで, 反射率と透過率を計算するためにポートを使用しない代替モデリング戦略を導入します. 代わりに, 上下に完全整合層 (PML) を使用してすべての反射光と透過光を吸収し, プローブを使用して反射率と透過率を計算します. PML は, 波動電磁気学の問題における PML の使用 に関するこちらのブログで説明されているように, 入射するあらゆる電場を吸収します.
PML は電場の伝搬成分とエバネッセント成分の両方を吸収しますが, ここでは伝搬成分のみを吸収するようにします. したがって, ここでも PML を材料界面から十分離して配置する必要があります. 前回と同じ経験則に従い, PML を材料界面から少なくとも半波長離して配置します.
斜入射角に近づくと, PML ドメインでさえデフォルトではすべての光を吸収するわけではありません. 斜入射角に近づくと, 吸収方向の実効波長が非常に長くなるため, PML 設定でデフォルトの波長を変更する必要があります (下図参照). この設定変更は, 約 75°を超える入射角に着目する場合にのみ必要です.
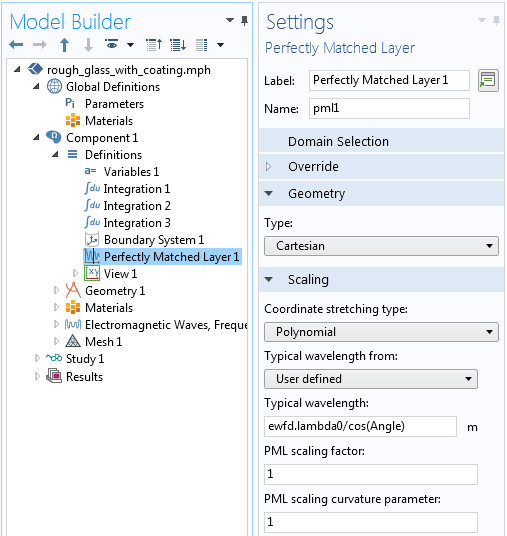
斜入射角を考慮して変更された PML 設定.
ドメインが上下に PML で区切られるようになったため, 波を発射するポートをモデリングドメイン内に配置する必要があります. そのためには, スリット条件 オプションを使用して, ドメインに裏打ちされた内部ポートを定義します. つまり, ポートはこの内部境界から一方向に波を発射することになります. 境界に向かって反射された光は, 妨げられることなく通過し, PML に吸収されます.
これは波を発射する良い方法ですが, 反射光の量を計算するためにポート境界条件を使用することはもうありません. 数百の回折ポートを追加する必要があり, 同様に, 総透過率を計算するためにも数百のポートが必要になるためです.
総透過光と反射光を監視するために, 代わりにモデルに2つの内部境界を導入し, PML ドメインの直前に配置します (上の図を参照). これらの2つの境界において, 入射光で正規化された上方向と下方向のパワーフラックスを積分し, 総反射率と総透過率を算出します. これらの境界における電力流束の積分をより正確に決定するために, 波長よりもはるかに小さい単層の要素で構成される境界層メッシュも導入します.
入射側では, このモニタリング境界を内部ポートの上に配置します. 入射ポートは, 物質界面に向かって伝播する平面波を導入します. 界面で反射された光はこの内部ポートを通過し, 反射率をモニタリングする境界を通過し, PML で吸収されます.
以下のプロットは, 透過率, 反射率, 吸光度のサンプル結果を示しています. これらは, 滑らかな表面や周期的に変化する表面の結果とは明らかに異なります. 入射角のスイープは, 法線から 85° で終了していることに注意してください. もちろん, 実行するランダムジオメトリのケースごとに, これらのプロットは若干異なります.
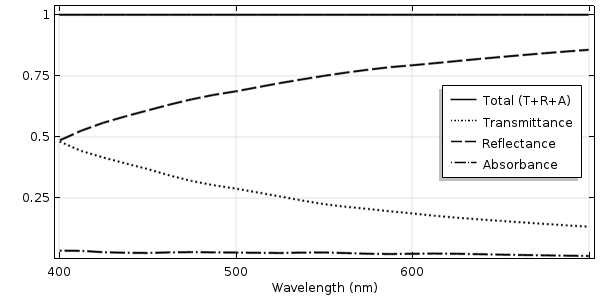
粗いガラス表面に垂直に入射した光の透過率, 反射率, 吸光度.
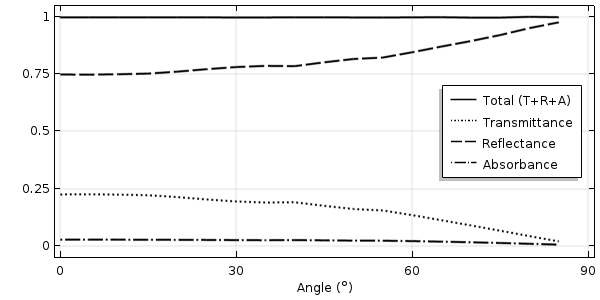
法線から最大 85° の入射角における 550 nm 光の透過率, 反射率, 吸光度.
粗い表面の光学特性計算に関する結論
ここでは, 粗い表面からの光透過率と反射率を計算するのに適したモデリング手法を紹介しました. この手法は, 均一な光学的に平坦な表面をモデリングする手法や, 周期的に変化する表面をモデリングする手法とは対照的です. 粗い表面のモデリング方法は, 異なる回折次数への散乱が重要でないときなど, 非常に長い周期を持つ周期構造のモデリングにも使用できます.
真にランダムな表面をモデリングするには, 形状を周期的に変更する必要があるため, ある程度の注意が必要です. さらに, 統計的に意味のある結果を得るためには, 検討対象となる領域サイズと異なるランダム形状の数が十分に大きくなければなりません. これには, 同じモデルの様々なバリエーションを解き, 結果の後処理が必要となるため, モデリングワークフローではアプリケーションビルダー, LiveLink™ for MATLAB®, または LiveLink™ for Excel® を使用すると便利です.
その他の参考資料
- 正弦関数の和として粗面を作成する方法 をご覧ください
- 手法を用いてランダム形状を作成する方法 をご覧ください
- 波動光学シミュレーションに関連するその他のブログをご覧ください:
MATLAB は The MathWorks, Inc. の登録商標です. Microsoft および Excel は, 米国およびその他の国における Microsoft Corporation の登録商標または商標です.






コメント (0)