
このブログは, 最小限の前提条件で弱形式を紹介することを目的としたシリーズの一部です. 最初のブログ では, 弱定式化の基本概念について学習しました. すべての方程式は解析形式のままでした. 今日は, COMSOL Multiphysics シミュレーションソフトウェアを使用して方程式を数値的に実装し, 解きます. COMSOL ソフトウェアの作業用コピーを使用して手順に従うことをお勧めします.
基本的な考え方のまとめ
前のエントリ で, 熱源のない定常状態での1D熱伝達の簡単な例を学習したことを思い出してください. ここで, 温度 T は, 区間 1\le x\le 5 で定義されたドメイン内の位置 x の関数です.
弱定式化により, 熱伝達物理の微分方程式が積分方程式に変換され, テスト関数 \tilde{T}(x) が積分関数内の局所的なサンプリング関数として解を制限します. 弱形式を部分積分すると, 微分階数が減るという数値的な利点が得られます. また, 熱流束に関して境界条件を指定する自然な方法も提供されます. 温度に関して固定境界条件の場合, 弱定式化ではテスト関数と同じメカニズムとその自然境界条件を使用して, 方程式系に追加の項を構築します.
最終的に, 次のような模範的な方程式にたどり着きました:
(1)
ここで, 左側の積分関数には温度の1次導関数のみが含まれ, 右側の最初の項は, 出力流束が左側の境界 (x=1) で 2 になる必要があることを定義します. 右側の他の2つの項は, 右側の境界 (x=5) で温度が 9 になる必要があることを指定します.
弱形式 PDE インターフェース
COMSOL Multiphysics で式 (1) を実装するには, モデルウィザードを使用して, 弱形式 PDE (w) インターフェース (数学 > PDE インターフェース の下) と 定常 スタディを含む新しい1Dモデルを作成します. 従属変数は, 式の表記と一致するように T に設定できます. ジオメトリについては, 1 から 5 までの 間隔 を作成します. デフォルトの 弱形式 PDE 1 ノードの下の弱式は, -test(Tx)*Tx+1[m^-2]*test(T) です. ここで, 最初の項は, 式の積分関数に対応します. (1) で, 2番目の項は熱源に対応しますが, これはこの簡単な例には含まれていないため, 入力フィールドから削除する必要があります.
弱式は次のように表示されます: -test(Tx)*Tx. ここで, Tx は, 温度の1次導関数である \partial_x T(x) の COMSOL Multiphysics 表記であり, test(Tx) はテスト関数 \partial_x \tilde{T}(x) の1次導関数です. 負の符号は, 入力フィールドが式が等号の右側にあると想定する規則 (設定ウィンドウの方程式セクションに表示) から来ており, 方程式の積分は左側にあります.
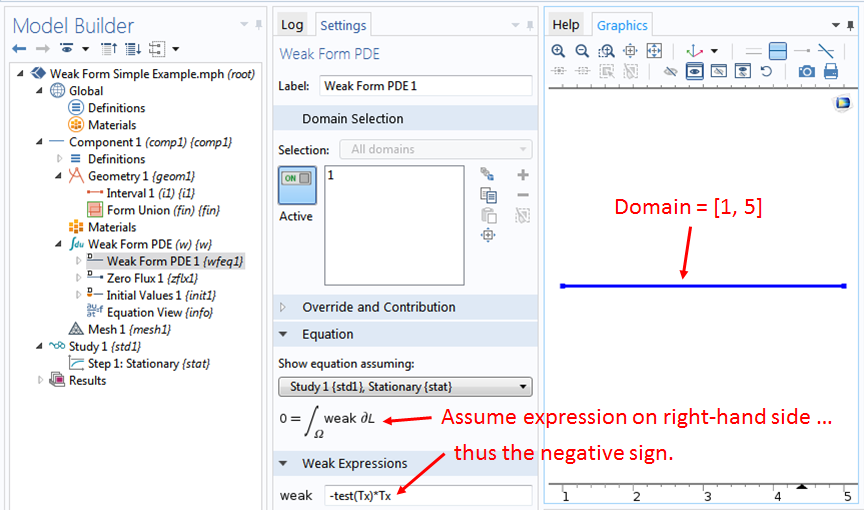
弱寄与機能
境界条件の式 (1) の右側の弱形式項を実装するには, 弱形式 PDE (w) ノードを右クリックします. ディリクレ境界条件 項目などの組み込み境界機能があり, ポップアップメニューで便利に使用できます. ただし, ここでは方程式を自分で入力することに関心があるため, ポップアップメニューの項目 More にマウスを移動し, 次のポップアップメニューの項目 弱寄与 をクリックします.
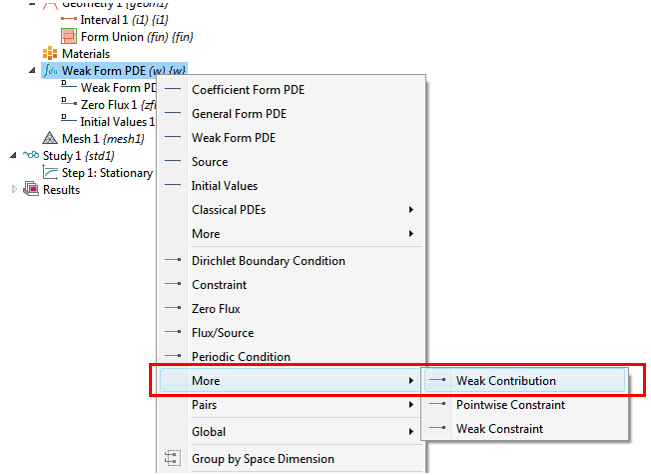
弱寄与 1 ノードの設定ウィンドウの 境界選択 で, ドメインの左端 (x=1) にある境界 1 を選択します. 次に, 同じ設定ウィンドウのセクション 弱寄与 に, 弱式を -2*test(T) として入力します. これにより, 境界 x=1 で出力流束が 2 になることを指定する, 式 (1) の右側の最初の項が処理されます.
固定境界条件
式 (1) の右側の最後の2つの項が一緒に T=9 を指定する, x=5 での固定境界条件については, ドメインの右端の境界 2 に別の弱寄与 ノードを作成し, その下に 補助従属変数 サブノードを作成します.
サブノードの 場の変数 名に lambda2 と入力し, 次に式内の2つの項として弱式を入力します. (1): -lambda2*test(T)-test(lambda2)*(T-9)
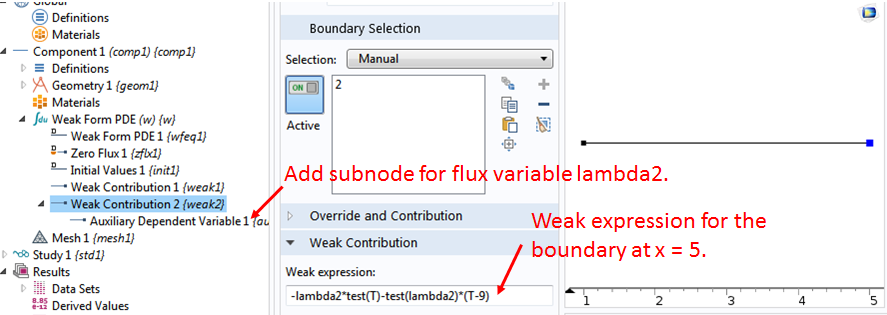
離散化
COMSOL ソフトウェアは, メッシュを作成してドメインを離散化します. メッシュ 1 ノードを右クリックして エッジ を選択し, エッジ 1 を右クリックして 分布 を選択します. 次に, 要素数を 4 に設定して 全てをメッシュ化 をクリックします. 後で離散化について詳しく説明するときにわかりやすくするため, 要素数を意図的に少なくしています.
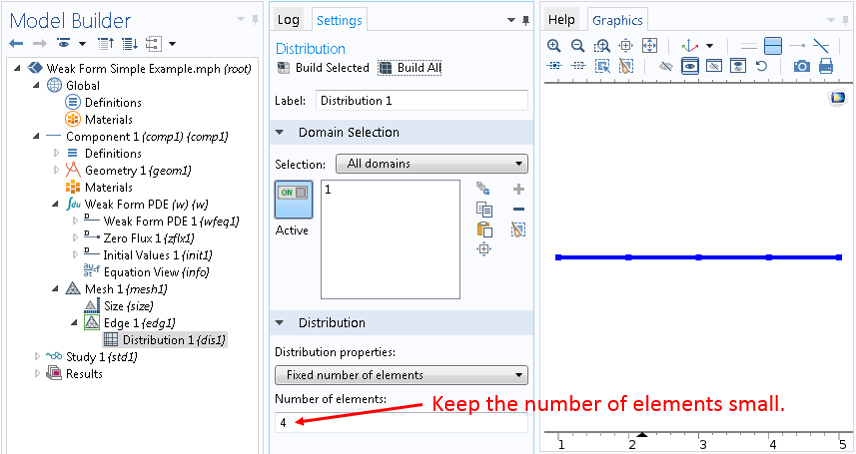
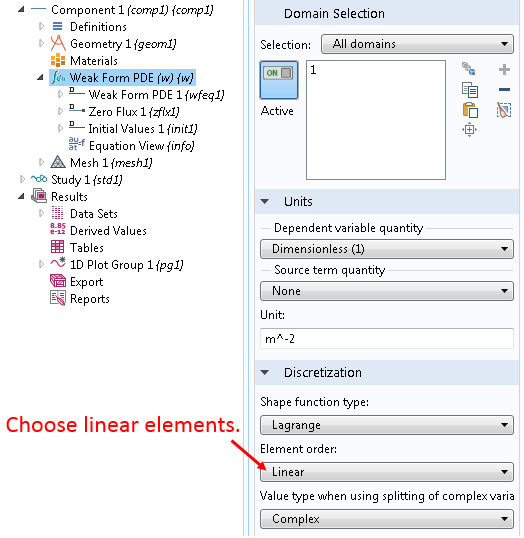
また, 弱形式 PDE (w) インターフェースノードの設定ウィンドウの 離散化 セクションで, 要素の次数を 1次 に設定します (モデルビルダーの 表示 ボタンをクリックし, ポップアップメニューの項目 離散化 をクリックして, 離散化 セクションを有効にします).
COMSOL Multiphysics で解を計算
これで, 計算 をクリックして, 解が意味をなすかどうか確認する準備ができました.
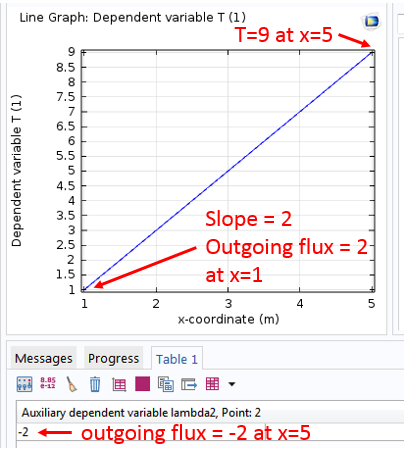
解はドメイン内で直線を示し, これは熱源のない定常状態での温度プロファイルと一致します. 直線の傾きは 2 で, これは x=1 で出力流束が 2 であるという境界条件と一致します. 温度は, 固定境界条件で指定されているように, x=5 で 9 です. 熱源がないため, 定常状態ではドメインから出力される熱流束の合計は 0 になるはずです. したがって, 出力流束は x=5 で -2 になるはずです.
以下のスクリーンショットに示すように, 熱流束変数 lambda2 の点評価を行うことで, これを簡単に確認できます:
読者の中には, 補助変数 lambda2, いわゆる ラグランジュ乗数 を解くことが常に必要かどうか疑問に思う人もいるかもしれません. 特に, モデル作成者には必要なく, 解くには必然的に計算量が増えるからです. 次のブログで説明するように, COMSOL Multiphysics には代替機能があり, ユーザーはラグランジュ乗数を解くかどうかを決定できます.
まとめと今後の予定
今日は, 弱定式化の概念を一新し, COMSOL Multiphysics で弱形式方程式 (1) の例を実装しました. 結果として得られる数値解は, 単純な物理的議論から予想されるとおりに動作します.
今後のブログでは, 式 (1) などの弱形式方程式がどのように離散化され, 数値的に解かれるかを “内部” から見ていきます. 同じ問題をさまざまな方法で解く方法や, さまざまなタイプの問題に対してさまざまな境界条件を設定する方法を確認します.
お楽しみに!





コメント (0)