
Newman モデルとその派生モデルは, さまざまな動作条件下でのリチウムイオン電池設計の動作を正確に予測するために使用される標準理論を形成します. Newman モデルでは, 電池電極の多孔質構造の形状は詳細に記述されません. 代わりに, 一般的な平均寸法が入力として使用され, 電極が均質で等方性の材料であると記述されます. しかし, このアプローチは, 詳細で不均質な形状モデルと比較してどの程度正確でしょうか? 調べてみましょう.
リチウムイオン電池のモデリングに対するさまざまなアプローチ
リチウムイオン電池モデリングの分野では, Newman モデルとその派生モデルが主流です. これらのモデルは, 多孔質構造の均質化に基づいています. 多孔質電極の詳細な3D形状を描画する必要はありません.
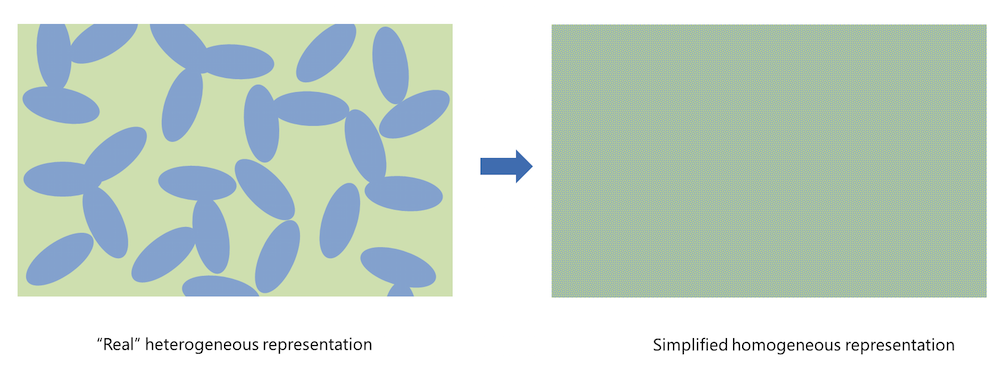
図 1. 均質化により, 実際の不均質多孔質電極構造が簡略化されます.
均質 Newman モデル
均質化とは, 実際の多孔質構造がスラブで近似され, 固体粒子 (上の図の左側で青で表示) と細孔電解質 (緑で表示) の完全に混合された溶液として扱われることを意味します. 均質な表現の結果, 細孔電解質 (イオン伝導体) と導電性電極粒子 (電子伝導体) は同じ幾何学的領域で定義されます. 次に, 多孔質構造と粒子の特定の形状の観察可能な効果を考慮するために, 多孔度や屈曲度などの変数を使用して, 有効な電荷と質量輸送特性が記述されます.
均質多孔質電極モデルでは, 電極材料と細孔電解質の間で電流を転送する電荷移動反応は, 溶液中の2つの化学種間の均質反応の定義と同様に, 電極領域と電解質領域のバランスの取れた電流ソースとシンクとして導入されます. カソード電荷移動反応は, 電子導体の電流バランスのソースであり, 細孔電解質の電流バランスの対応するシンクです. 物質バランスには, 均質化された電荷移動反応の化学量論に従って, ファラデーの法則から対応するソースとシンクが含まれます.
これらのタイプの多孔質電極モデルは, さまざまなタイプの電気化学セル内の 多孔質電極のモデリングとシミュレーションで十分に機能してきました. しかし, これらのモデルは, リチウムイオン電池の多孔質構造の詳細設計を説明するのにどの程度有効でしょうか. Tommy Zavalis (電池の専門家, 元同僚, 現在の COMSOL の顧客) と私は, スウェーデンでの “神聖な” コーヒーブレイクの1つでこの質問について話し合いました. 私たちの結論は, 均質モデルと不均質モデルを比較するまで, この質問の答えはわからないというものでした. そこで, 理想的な3D多孔質電極ジオメトリの Newman モデルを検証するために, 不均質モデルを構築しました.
不均質モデルの構築
不均質モデルでは, 電子伝導性粒子と細孔電解質が3Dで明示的に記述され, モデリング空間内の2つの別個のドメインとして扱われます.
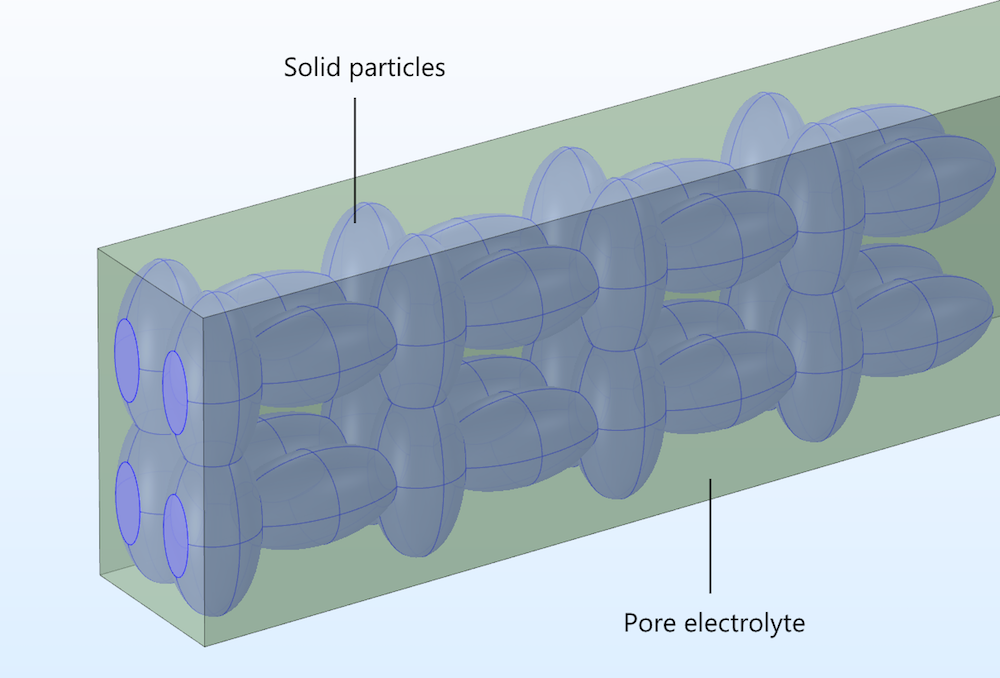
図 2. 理想的な多孔質構造における細孔電解質と粒子領域.
イオン伝導体の電流保存は細孔電解質領域でのみ定義され, 導電性粒子の電流保存は固体電極領域でのみ定義されます. イオンの質量輸送は細孔電解質領域でのみ定義され, 固体粒子の表面は, イオンまたは他の溶液種が不均一な電子移動によって反応できる境界を形成します. これは, 物質収支と反応が均質化された電極領域全体で定義される均質モデルとは対照的です.
固体粒子の表面で形成されたリチウム金属は, 粒子領域自体でのみ拡散し, 粒子表面が外部境界としてモデル化されます.
Newman モデルの精度の評価
ここで, Newman モデルと不均一モデルが詳細な3D構造をどの程度正確に記述するかを比較できます. 簡単なモデリング実験として, リチウムイオン電池の負極と正極に使用する, 理想的な3D多孔質構造を持つ理想的なユニットセルを構築します. 下の図に, 自由電解質と細孔電解質内の電流の流れを示す流線を含む形状を示します. 電極粒子は, 電子伝導体のマトリックスを形成するために, 長軸を異なる方向に回転する楕円体で構成され, 細孔電解質は粒子間の空隙に含まれています.
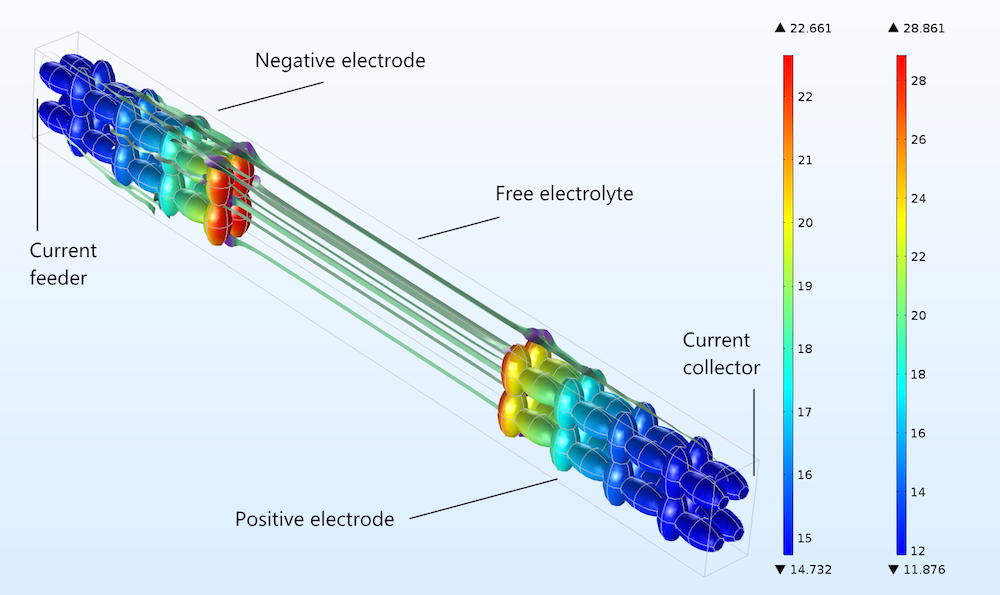
図 3. 右側の形状と色の凡例に示されている正極と, 左側の形状と色の凡例に示されている負極の電荷移動電流密度 (A/m2) 分布.
上の図は, 放電中の固体粒子の表面における電荷移動電流密度の絶対値を示しています. プロットは, 電極の集電体と給電器に面する側が, 電極間の自由電解質 (またはセパレーター) に面する側よりも利用率が低いことを示しています.
粒子の回転を変更して, 全体的な空隙と固体の比率 (多孔度) を一定に保ちながら, 電極の深さに沿って2つの異なる多孔度分布を作成できます. Newman モデルは, 入力として普遍的な平均多孔度のみを使用するため, このような変化があっても結果が変わることはありません.
図 3 の電極を, 下の図の正極に示すように 180° 回転させると, 電流密度分布に違いが生じますが, この違いは非常に小さいです (2つの図の色の凡例を比較するとわかります). このような小さな電流分布の違いは, 以下で説明するように, 電気化学インピーダンス分光法でも検出できません.
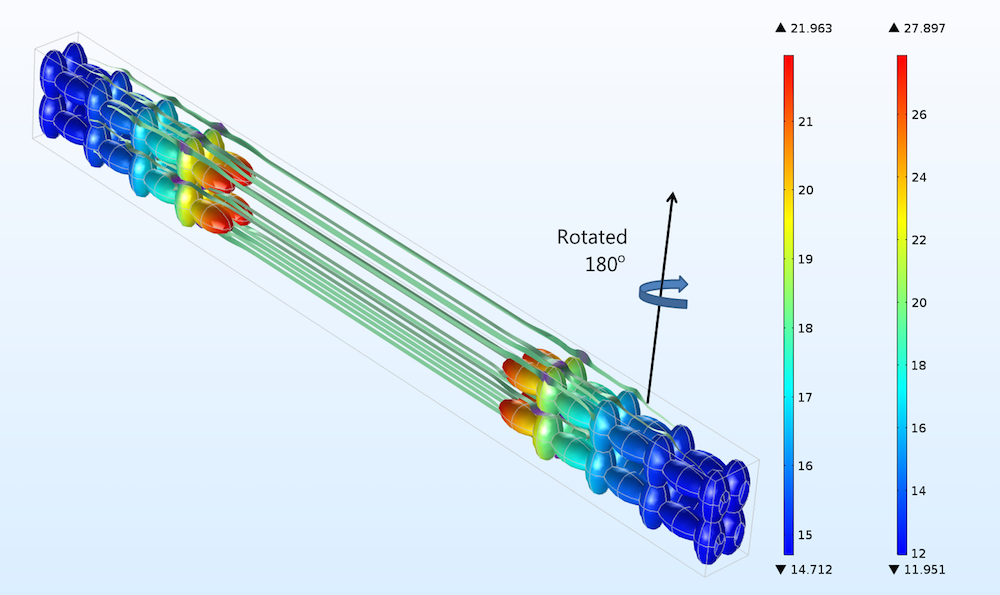
図 4. 正極 (右) と負極 (左). 正極と負極の両方が水平面内で 180° 回転した場合の図です. 図 3 と比較してください (上記では正極の回転のみが示されています).
コーヒーを飲みながらの議論で, Tommy と私は, 電極内のサブプロセスを異なる時間スケールで分離する電気化学インピーダンス分光法 (EIS) のような方法であれば, 異なる形状の違いを捉えることができるだろうと推測しました. そのため, 私たちは, 異種ジオメトリと同種 Newman モデルの両方に対して EIS 実験をシミュレートすることを選択しました.
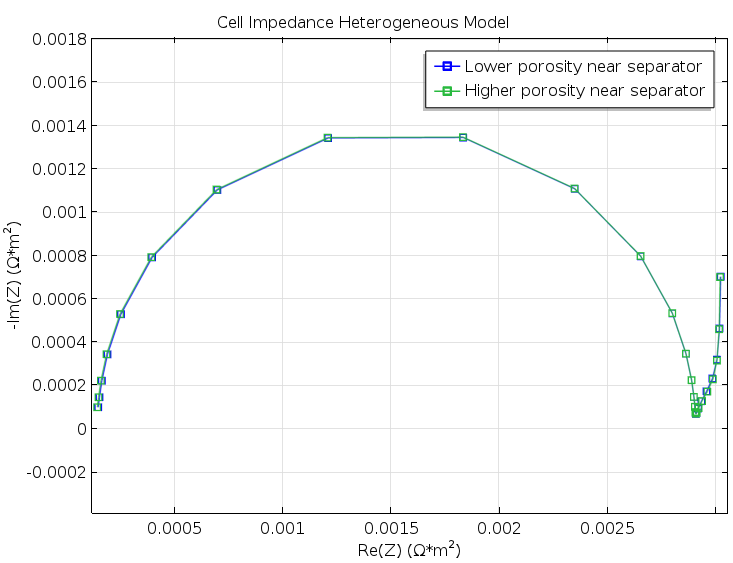
図 5. 図 3 と 図 4 の2つのモデルジオメトリのナイキストプロット. 違いは非常に小さく, 実際の実験では検出されなかったでしょう.
結果は有望であると同時に残念なものでした. 残念なのは, 図 3 と 図 4 のケースの構造の小さな変化が, 図 5 に示すように, 2つのジオメトリのモデリング実験のナイキストプロットに現れていないためです. しかし, 結果は有望です. なぜなら, Newman モデルは, フィッティングをまったく行わずに, 不均質モデルとかなり一致するからです (下の図を参照). これは, 理想化された構造の詳細が粗すぎて効果的に均質化できないように見えるため, 多少意外です. たとえば, 粒子のサイズは, モデル化された単位セルの幅よりも1桁小さいだけです.
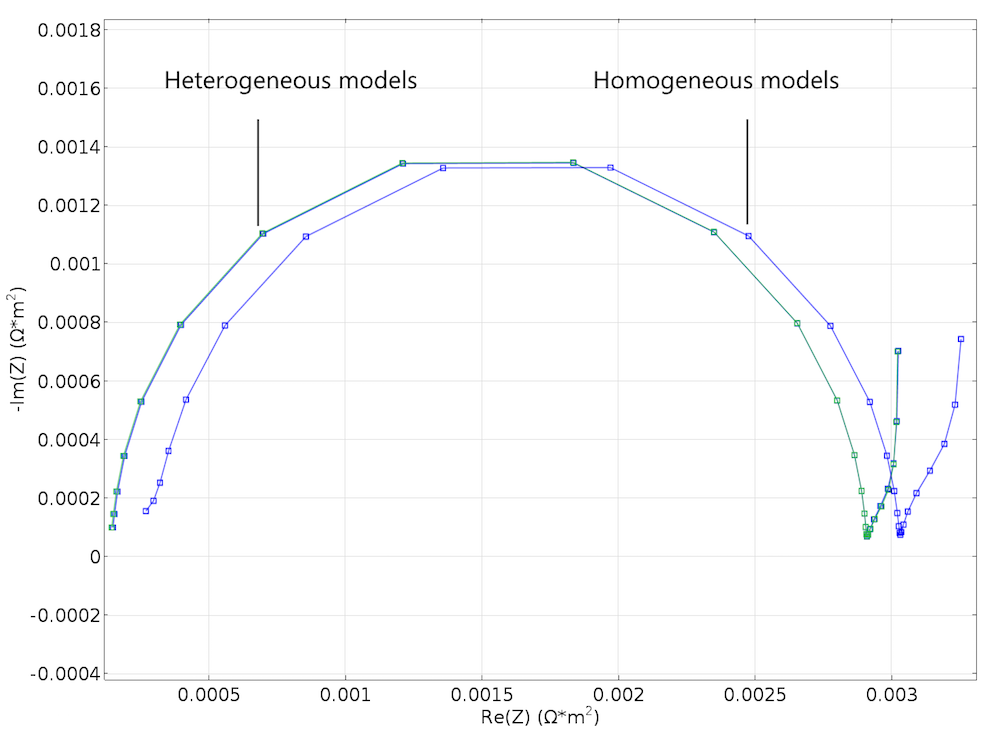
図 6. Newman モデルを使用して EIS 実験をシミュレートして作成されたナイキストプロット. 図 5 の異種モデルの対応するプロットとよく一致しています.
Newman モデルと異種モデルを使用したリチウム電池のモデリングに関する結論
もちろん, この件に関する最後の言葉はまだ出ていません. 非常に単純な構造をシミュレートしましたが, 電極を回転させることによって得られる構造の変化は明らかに小さすぎて, 結果に劇的な影響を与えることはできません. 自然な次のステップは, 一定の平均特性の下で詳細な説明でより大きな変化を試すことです. そうすれば, 均質な Newman モデルでは捉えられない, 異なる不均質構造で結果に違いが出る可能性があります.
自分で試してみませんか? 以下のリンクでは, このブログで紹介されているモデルの短いプレゼンテーションと, 上記の結果を生成するために使用した COMSOL Multiphysics ファイルをご覧ください. ジオメトリに大きな変化を加えたり, モデルを開始点として使用してゼロから独自のジオメトリを作成したりできます.
これらの出版物もご覧ください:
- J. O’M. Bockris and A. K. N. Reddy, Modern Electrochemistry Volume 2, Springer-Verlag, 1970.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems 3rd Edition, Wiley, 2004.






コメント (0)