不均一触媒作用のモデリングアプローチ

不均一触媒のモデリングは, このタイプの触媒を利用する工業プロセスが多数あるため, 化学工学コミュニティから伝統的に大きな関心を集めています. ここでは, 詳細なマイクロジオメトリから始めて, 均質化を通じて近似を進める手順について説明します. この手順に従うことで, ミクロレベルの粒子からマクロレベルの反応器レベルまで, 触媒を詳細に設計し, この設計が反応器全体のパフォーマンスに与える影響を研究できます.

不均一触媒の概要

バルク化学物質とファイン化学物質の膨大な生産量と, 不均一触媒に基づくプロセスにおける環境に有害な化学物質の大規模な除去に刺激されて, 科学および工学コミュニティはこの主題に非常に興味を持っています. また, 数学的モデリングとシミュレーションを通じてこれらのプロセスを理解することにも大きな焦点が当てられています.

不均一触媒は, 2つの異なる相の界面での触媒反応に関係します. ここでは, 工業プロセスにおける最も一般的な不均一触媒である固体-流体界面における不均一触媒についてのみ説明します. このようなプロセスでは, 反応物と生成物は固体触媒表面と接触する流体混合物中に存在し, そこで触媒反応が起こります.

固体-流体 不均一触媒 に基づく一般的な大規模工業プロセスには, Haber-Bosch 法でのアンモニア, Ostwald 法での硝酸, Wacker 法でのエチレンオキシド, 水蒸気改質による水素, Ziegler-Natta 重合でのポリエチレンとポリプロピレンの生成などがあります.

電気触媒の表面での電気化学反応も不均一触媒に分類されます. 電気触媒に基づく大規模工業プロセスの例としては, 塩素アルカリ, 塩素酸塩, 水分解プロセスがあります.

自動車産業で使用される触媒コンバーターは, 窒素酸化物を窒素と酸素に還元する工程の1つであり, 不均一触媒に基づく広く使用されているプロセスのもう1つの例です. 環境の観点から重要な他のプロセスには, 石油の脱硫と二酸化硫黄の触媒酸化があり, どちらも石油製品の燃焼中に環境への硫黄酸化物の排出を減らすことを最終目標としています.

吸着された分子のごく微量を検出できるセンサーは, 多くの場合, 不均一触媒に基づいています. 水素センサーと酸素センサーは, 電気触媒を介して動作するセンサーの例であり, 酵素反応に基づくバイオセンサーも同様です.

主な手順

不均一 触媒の触媒は, 均一 触媒の場合と同じように, 触媒反応の活性化エネルギーを下げることによって作用します.

触媒が実際にこれを実現する方法については説明しませんが, ほとんどのプロセスには2種類の固体触媒, つまり酸触媒と金属触媒 (G. F. Froment, K. B. Bischoff, J. De Wilde 著 Chemical Reactor Analysis and Design による) が関係していることを簡単に述べておきます. アルミノケイ酸塩などの酸触媒は, ルイス酸またはブレンステッド酸として作用し, このようにして活性化エネルギーが低い表面錯体を形成します. 金属触媒は主に, 吸着された水素の表面複合体を伴う水素化および脱水素化反応に関係しています.

不均一触媒反応における化学種の主なステップは, 次のように説明できます (Chemical Reactor Analysis and Design および H. S. Fogler の書籍 Elements of Chemical Reaction Engineering による):

1. 混合物のバルクから触媒粒子への反応物の輸送
2. 触媒粒子の細孔内の反応物の活性部位への輸送
3. 反応物の活性部位への吸着
4. 吸着された生成物を形成する反応物の反応
5. 活性部位からの生成物の脱着
6. 触媒粒子の細孔内の生成物の輸送触媒粒子を粒子から取り出す
7. 粒子から混合物のバルクへの生成物の輸送

下の図は, 触媒粒子の断面でこれらの7つのステップを模式的に示しています. 触媒粒子は, 触媒担体の粒子で構成されています. 活性部位はアプリコット色で, 触媒担体の表面 (青いパターン) に配置されています.

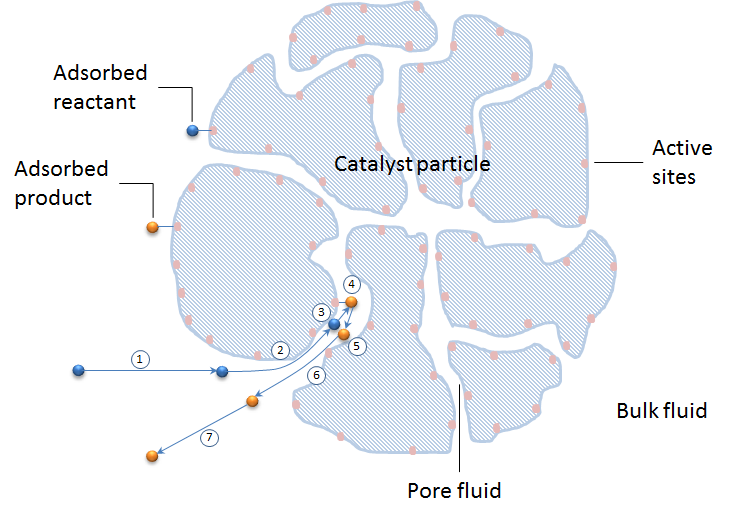
これらの7つのステップの可能なモデリングアプローチを見てみましょう. また, 反応混合物のバルク内の物質収支を含む, 触媒反応器全体のモデルに7つのステップがどのように組み込まれるかを調べることもできます.

吸着-脱着モデル

吸着には主に2つの種類があります. 物理吸着と化学吸着です.

物理吸着はファンデルワールス力によって起こりますが, 化学吸着は共有化学結合を伴います. 不均一触媒では, 化学吸着は通常, 触媒反応の必須部分です. したがって, ここではこの種類の吸着のみを取り上げます.

不均一触媒における化学吸着の最も一般的な説明は, Langmuir 等温線によるものです. Langmuir 等温線の理論は, 次の仮定に基づいています:

1. 吸着は, 異なる吸着部位および異なる表面被覆率でエネルギー的に均一
2. 吸着された化学種は単層を形成すると仮定
3. 吸着された分子間に相互作用はない

ここで, 表面被覆率は, 占有されている吸着部位の割合を指します.

Freundlich 等温線は, 吸着が不均一であり, 一部の部位の吸着係数が高く, 最初に分子で覆われるという仮定に基づいています. これらの部位の吸着熱はより発熱的です. 吸着熱は, 表面被覆率に対数的に依存します. Temkin 等温線は, 吸着熱が表面被覆率に線形依存すると仮定することで得られます. BET 等温線などの他の吸着モデルにも分子の複数の層が含まれており, その説明には物理吸着を含める必要があります.

表面反応

化学反応工学の要素 によると, 不均一触媒のモデリングでは, 3つの可能な反応メカニズムがよく使用されます.

単一サイト 反応メカニズムは, 分子の吸着と, この単一サイトでのその 異性化 または分解を表します. 下の図は, 分子の異性化の例を示しています.

双対サイト 反応メカニズムは, 反応物分子の吸着を記述します. この反応物は, 生成物が吸着される別の自由サイトと相互作用します. 双対反応メカニズムは, 2つの反応物が異なるサイトに吸着され, 吸着された種が反応して生成物を形成することも記述します (下の図を参照).

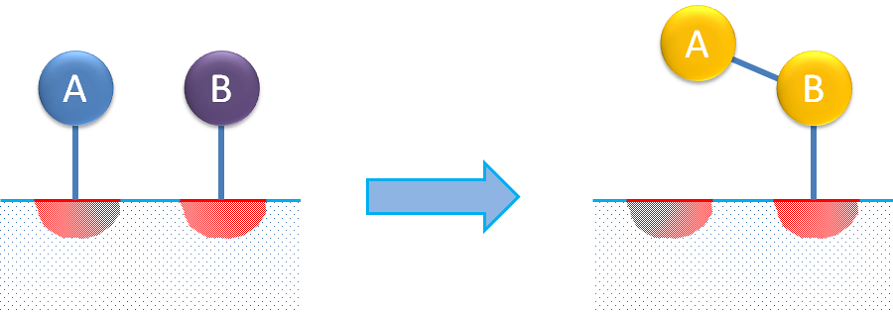
双対サイト反応と単一サイト反応は, 通常, Langmuir-Hinshelwood または Hougen-Watson の速度論に従うと考えられています.

3つ目の表面反応メカニズムは, 反応分子が単一サイトに吸着され, 吸着された種が流体内の分子 (吸着されていない) と反応して吸着生成物を形成することを説明しています. これは通常, Eley-Rideal メカニズムと呼ばれます.

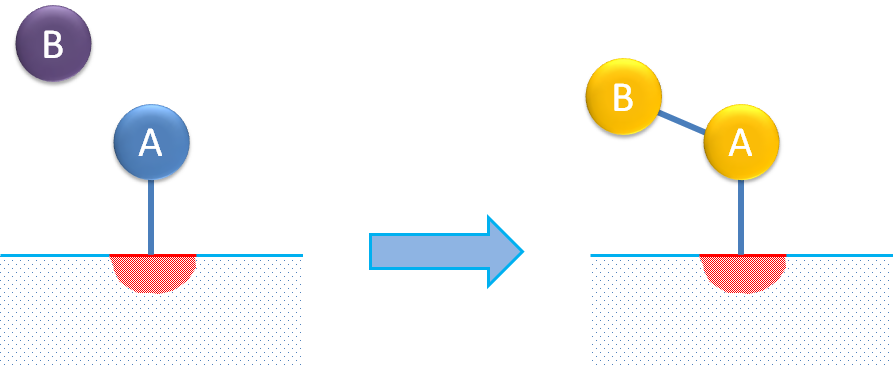
最も単純な単一部位反応メカニズムであっても, 全体的な速度式は, 単一の式として解析的に表現すると比較的複雑になる場合があります. 次の全反応に従って異性化の例を見てみましょう:

(1)

反応機構は次のように表すことができます:

(2)

ここで, S は活性部位, AS(ads) は吸着された反応物, BS(ads) は吸着された生成物, B は生成物を表します.

この単純なメカニズムでも, 質量作用の法則と反応1と3が定常状態に近いという単純化を使用した反応速度式は比較的複雑です (G. F. Froment, K. B. Bischoff, J. De Wilde が Chemical Reactor Analysis and Design で示したように):

(3)

この式で, \theta は, 占有されていない活性部位の表面濃度 {c_A} を表し, {c_B} はそれぞれ異性体 A と B の濃度です. {K}, {k_1}, {k_2}, および {k_3} は定数です.

数値法を使用する場合, メカニズムの全速度式を導出する必要はありません. この場合, メカニズムの化学式を入力するだけで済みます. 代わりに, 各ステップの速度定数の推定値と, プロセス開始時の表面濃度の推定値を与える必要があります.

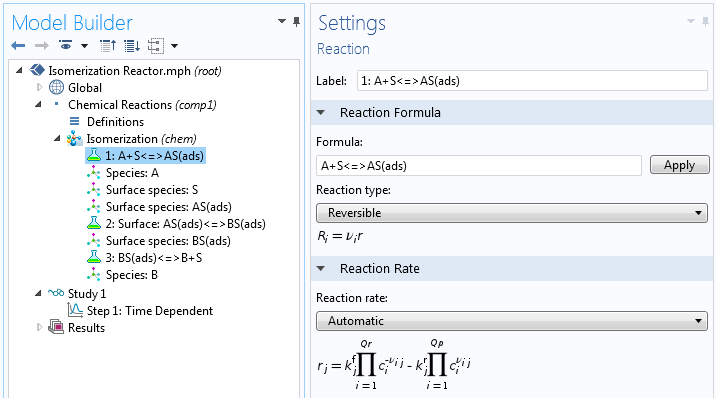
解析式を導出することと, 簡略化せずに完全な反応メカニズムを入力することを組み合わせることも, 良い代替手段です. その理由は, 解析式には, 反応の全反応速度の測定から得られる定数と中間濃度の積が含まれているからです. これらの製品を使用して, 詳細なメカニズムのすべてのステップの反応速度を推定できます. さらに, この組み合わせたアプローチにより, 簡略化の仮定がどの条件で有効であるか, およびモデルで反応の完全なセットを使用する必要がある場合を解析できるようになります.

輸送ステップ

バルクおよび多孔質触媒内の輸送の説明は, 微視的スケールの粒子レベルで実行でき, 触媒粒子と細孔形状が詳細に記述されます. さらに, 触媒が非常に活性である場合, 多孔質構造は必要なく, 形状も詳細に記述できます.

ただし, 細孔が触媒形状の典型的な代表単位セルのサイズに比べて非常に小さい場合, またはこの単位セル内の細孔の数が多すぎる場合は, 多孔質触媒の詳細な形状記述は実行できません. この段階では, 多孔質触媒構造の均質化された記述を使用できます.

触媒の微細構造を均質化モデルで処理すると仮定します. 反応器全体のバルク混合物の輸送を研究する場合, 詳細なモデルを使用して粒子で構成される構造を記述することができます.

粒子の数が多くなりすぎて粒子ベッドの形状が複雑になりすぎると, バルク混合物のスケールでの均質化も使用する必要があります.

これら4つの可能なモデリングアプローチを見てみましょう:

1. 微視的触媒構造の詳細な説明
2. 各粒子の均質化された説明
3. 個々の粒子の説明が均質化された多数の粒子の構造の詳細な説明
4. 粒子の均質化された説明と組み合わせた粒子層の均質化

微視的スケール

X 線マイクロトモグラフィー の開発と, モデリングやシミュレーションに携わるエンジニアや科学者が利用できる計算性能の向上により, 非常に複雑で不規則な構造をモデリングする可能性が高まっています.

電池内の多孔質触媒の小さな部分.

さらに, 触媒と細孔の形状が明確に定義された微細構造を製造できるようになったことで, 詳細な形状を使用してこれらの規則的な構造を研究することへの関心も高まっています. 上の図に従って, 規則的な形状の流路で構成された触媒粒子の仮想例を見てみましょう. この形状は, 約100個の重なり合った触媒粒子で構成され, それらが一緒になって直径約10マイクロメートルの球状の触媒粒子を形成します. 触媒粒子間の空隙は, 曲がりくねったマイクロ流路システムを形成します.

物質収支の式は, ドメイン内の蓄積と流束のバランスを記述します. 吸着, 反応, 脱着プロセスは, 触媒粒子の表面の境界条件として記述されます. 粒子自体はモデリングドメインの一部ではなく, 粒子の外側の流体と粒子内部の細孔内の流体のみがモデリングドメインの一部です. 均一な反応がない場合の流体内の種 _i の物質収支は, 次のようになります:

(4)

ここで, {{\bf{N}}_i} は, 化学種 _i の流束ベクトルを表します.

触媒表面を表す境界での種の流束は, 触媒反応における化学種 _i の消費または生成に対する反応速度 R_i によって与えられます.

(5)

ここで, {\bf{n}} は, 触媒の表面に対する外向きの法線ベクトルを表します.

下の図は, 粒子の周りの流れと反応物の濃度のシミュレーション結果を示しています. 表面プロットは, 触媒粒子の表面で反応する種の濃度を示しています. 流線は速度場を示しています.

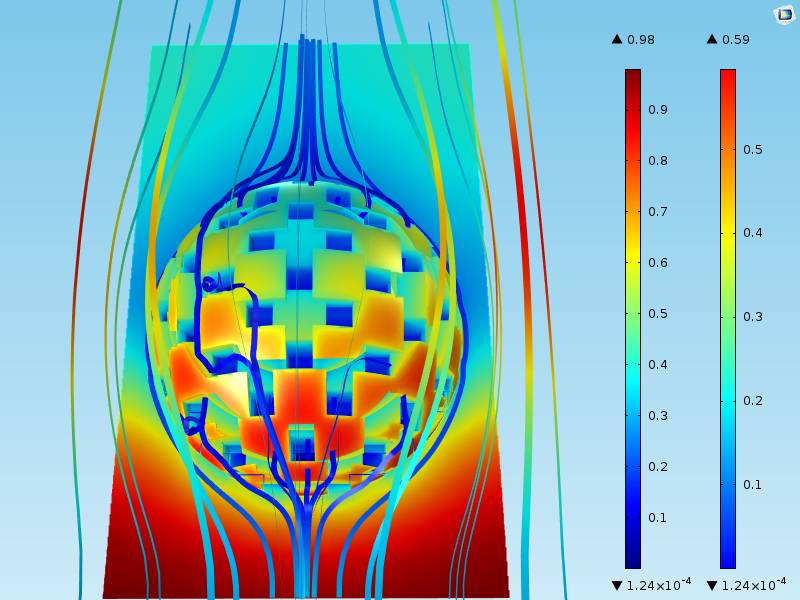
粒子の周りのバルク内の濃度は, 入口 (領域の下部) の 0.98 mol/m³ から出口 (領域の上部) の約 0.4 mol/m³ まで変化していることがわかります. さらに, 球の下部にある触媒粒子表面の最高濃度は 0.59 mol/m³ です. これは, 流体が球体の下部にある触媒粒子と最初に接触した場合でも, 濃度が約 0.30 mol/m³ (= 0.98-0.59) 変化する 質量輸送 境界層が存在することを意味します.

球状触媒粒子の周囲では, 球体と球状表面の濃度差が異なります. この質量輸送境界層は, 上記の “主な手順” セクションで概説したリストのステップ1に相当します.

反応分子のすべてが触媒粒子の外表面で消費されるわけではありません. 一部の分子は多孔質構造に拡散し, 後に細孔壁の表面, つまり多孔質粒子内部の触媒粒子の表面で吸着して反応します. この輸送プロセスは, リストのステップ2に相当します.

微視的スケールでの均質化

多数の粒子をモデル化する場合, 上記と同じ詳細レベルで形状をモデル化することはできません. その場合, 均質化によって多孔質構造をモデル化できます. 基本的に, これは多孔質粒子を流体と触媒の両方を含む均質なスラブとして扱うことを意味します. 流体は, 粒子の多孔度と曲がり具合に依存する有効な輸送特性を持つ記述の多孔度を使用してモデル化されます.

均質化後, 吸着, 反応, 脱着プロセスは物質収支のソースとシンクになります. 言い換えると, これらはもはや流体領域への境界条件として記述されません. 代わりに, 反応は触媒粒子の多孔質領域内のソースまたはシンクとして表されます.

(6)

この式で, {S_a} は粒子の特定の触媒表面積, つまり単位体積あたりの表面積を表します.

さらに, 2つの異なるモデリング領域と, 2つの異なる領域方程式のセットがあります. 1つは触媒反応項のない粒子を取り囲むバルク流体用で, もう1つは多孔質粒子用です. これら2つの領域間の内部境界では, 濃度と化学種の流束に連続性があります.

また, 流体流れ方程式にも連続性があります. バルク流体の場合は ナビエ・ストークス方程式 で記述されますが, 多孔質領域では Brinkman 方程式で流体流れを記述できます.

下の図は, 表面と均質化粒子の周りの流れ場と濃度を示しています. 表面は多孔質ペレットの外側表面の濃度のみを示していることに注意してください. 上記の詳細なケースでは, 表面プロットは粒子の表面から粒子の中心までを表していました.

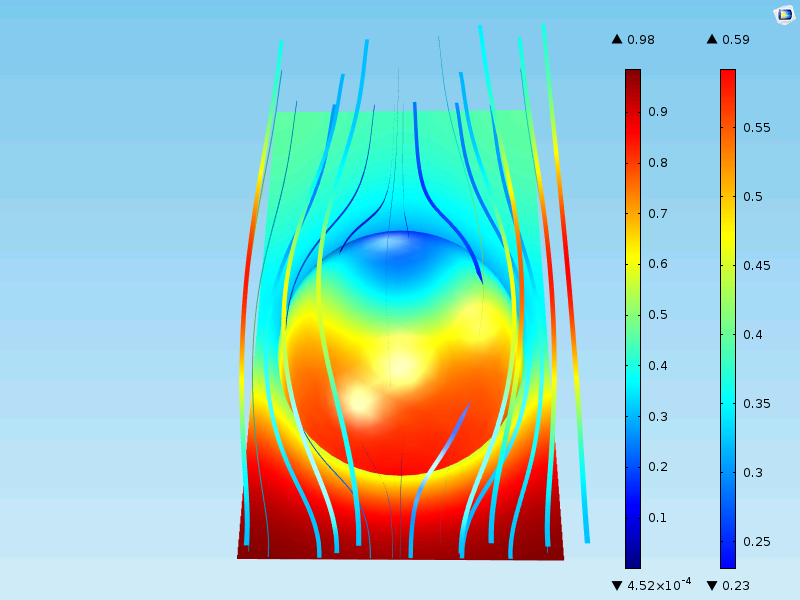
結果は, 完全な幾何学的説明を含む結果に近いです. ペレットの表面の最大濃度は 0.59 mol/m³ で, 最小値は粒子の中央でほぼ 0 mol/m³ です. これは, 詳細な説明の場合と同じです. また, ユニットセルの出口は, 詳細な説明の場合と同じように, 約 0.40 mol/m³ です.

なぜ, かなり一致しているのでしょうか? そうですね, それは, 詳細なジオメトリ内の触媒粒子が粒子全体のサイズに比べて比較的小さいためです. 触媒粒子が大きく, 形状がより不規則になると, 均質化はそれほど正確な説明ではなくなります.

均質化の場合と詳細な場合の粒子内部の濃度を調べることも興味深いかもしれません. 下の図は, 粒子内の濃度分布も均質化モデルで適切に説明されていることを示しています. 均質化モデルを設計目的で使用する場合, 粒子内部の輸送と反応を適切に説明することが非常に重要です. 反応分布は, 触媒の内部部品が吸着, 反応, および脱着プロセスでどれだけ使用されているかを示します. 内部部品が使用されない場合, 実際には多くの触媒材料が無駄になっているため, 代わりに モノリシック反応器 のような非多孔性触媒を使用する場合があります. 非常に活性の高い触媒の場合, 多孔質粒子によって提供される表面積の拡大は通常必要ありません.

多数の均質化粒子のマクロスケールでの詳細な説明

均質化粒子モデルによって詳細な形状の適切な近似が得られることがわかったら, この近似を使用して固定床反応器内の多数の粒子を説明できます. 例としては, マイクロテクノロジーを使用して詳細な形状を構築できるマイクロ反応器があります. このような反応器は, 詳細な速度論的研究やラボオンチップ (LOC) デバイスに使用できます.

また, この場合, 2種類のドメインがあります. 1つはバルク流体用, もう1つは多孔質粒子用です. また, バルク流体と多孔質粒子の間の内部境界を横切る流束と濃度の連続性も見られます.

ここで, 触媒粒子の外側のバルク混合物でも濃度が小さい値に減少します. 粒子の表面の最大濃度は依然として同じで, 0.59 mol/m³ です. これは予想どおりです. 最初の列の粒子は, 上記の単一粒子モデルとほぼ同じ入口を経験するからです.

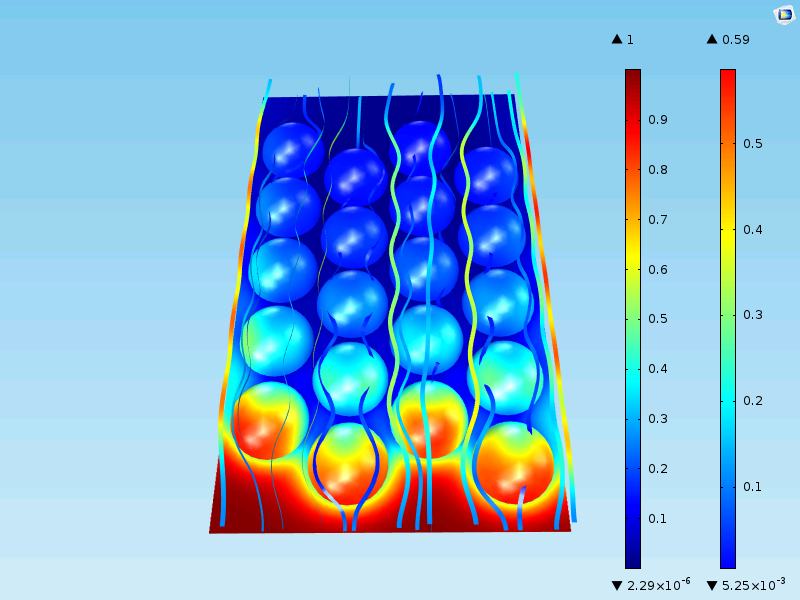
下の図は, 入口から出口までの2つの垂直線に沿った濃度のプロットを示しています. 1つの線は粒子の少し上の平面を走り, もう1つの線は粒子の中心の位置に沿った平面を走ります. 粒子に近い線 (緑) に沿った曲線は, 波状のパターンで粒子の位置を示していることがわかります. 粒子から少し離れた線に沿った濃度曲線は, 拡散 によって平滑化されているため, 滑らかです. 入口から出口までの反応器に沿った平均濃度は, 緑と青の曲線の中間のどこかにあります.

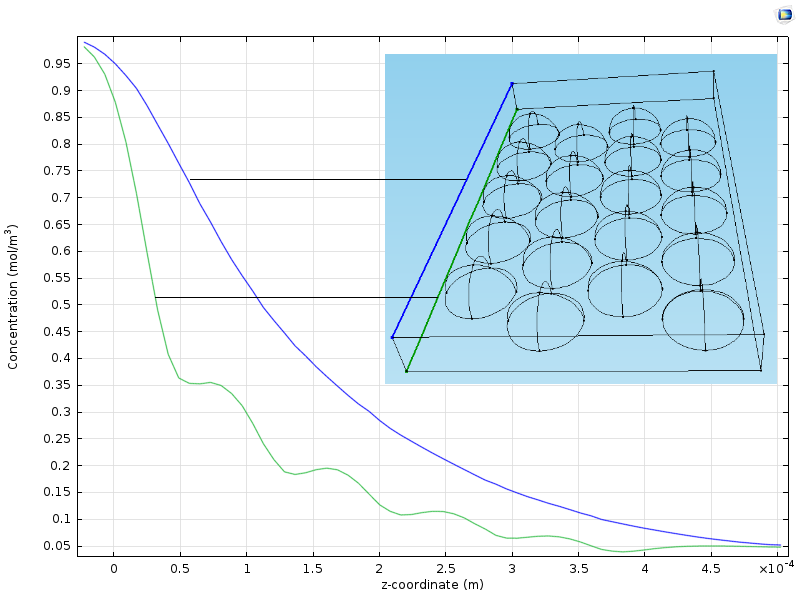
マクロスケールでの均質化の説明

上記の例では, 触媒粒子の内部に対して最初の均質化を導入しています. 下の図を参照してください:

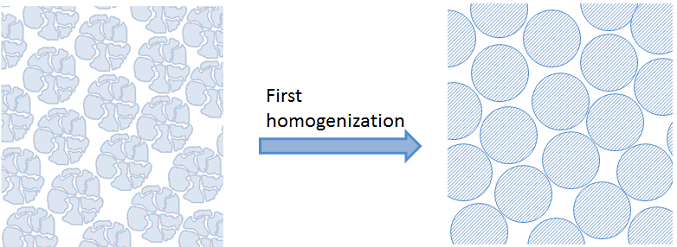
固定床反応器内の粒子が多すぎる場合, 粒子も固定床の寸法に比べて非常に小さくなります. その場合, 床の詳細な形状を記述する余裕はありません. 代わりに, 固定床と固定床内のバルク流体に対して第2の均質化を使用できます.

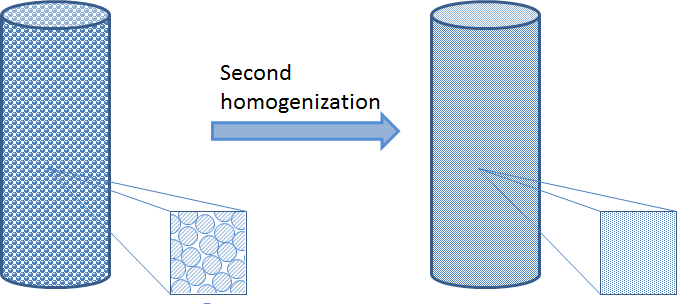
多孔質粒子はベッドのサイズに比べて非常に小さいため, 多孔質バルク領域内のソースとシンクに粒子を圧縮できます. ただし, この均質化では, すべての粒子を取り囲む境界層を横切る輸送と多孔質粒子内の輸送反応プロセスの記述を維持する必要があります. また, 多孔質バルク領域内の輸送と流れのおおよその記述も維持する必要があります. 均質化されていない粒子に描かれている原理については, 下の図を参照してください. これは, 固定ベッド内のすべてのポイントに独立変数 r を導入することで実現できます. これは, この粒子のすぐ外側の境界層を含む多孔質粒子の半径に対応します.

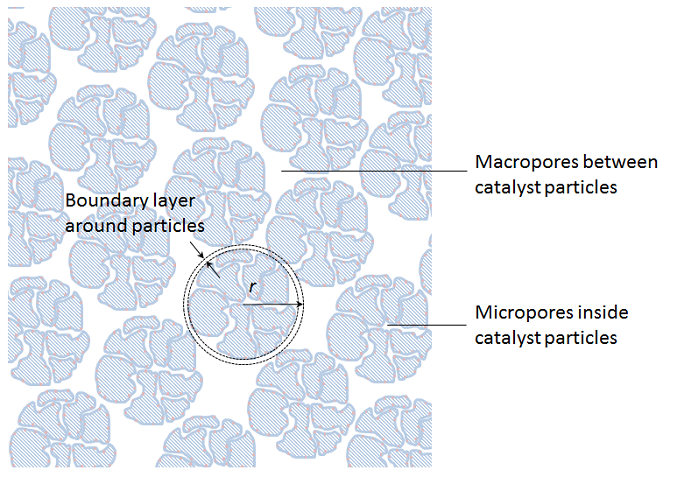
境界層内の輸送と粒子内部の輸送反応プロセスは, 半径に沿った球対称の物質収支で近似されます. 上記の例の詳細モデルにおける移流流束は主に軸方向 (粒子を横切って上下方向) に流れますが, 2番目の均質化では粒子の半径方向の変化のみが考慮されています. ただし, この移流の一部は, わずかに増加した有効拡散率として考慮される可能性があり, 簡略化された説明では分子拡散に加えて分散も生じます.

固定床を3次元でモデル化すると, 実際には, 粒子半径に沿った変数として, x, y, z, r の4つの独立した空間変数が得られます. 5番目の独立変数は時間です. さらに, いわゆる バイモーダル多孔度記述 を使用する必要があります. これは, 触媒粒子内のミクロ多孔度と, バルク混合物が流れる粒子間の空隙のマクロ多孔度を記述します (上の図を参照).

粒子レベルの1D輸送反応方程式と固定床のバルクとの結合は, 多孔質バルク領域のソースとシンクとして多孔質粒子の内外への流束を導入することによって得られます. 逆に, バルク領域の局所濃度は, 多孔質床のすべてのポイントにおける粒子モデルの境界層の濃度の境界条件です.

1つの濃度の多項式として記述される比較的単純な反応速度論を持つ定常状態モデルの場合, 粒子の半径 (境界層を含む) に沿った輸送反応プロセスを解析的に解くことができます. この解は, Thiele 係数 といわゆる 有効係数 を使用して, さまざまなタイプの粒子と運動反応順序ごとに表にまとめられています. このような場合, 多孔質粒子に出入りする流束の解析式は, 固定床内の流体の大部分の物質収支のソースとシンクとして使用されます.

また, マクロスケールでは, 均質化近似の精度は, 固定床のサイズと比較した粒子の相対的なサイズに依存します. 近似の精度は, 粒子のサイズが小さくなるにつれて高くなります.

また, 興味深い点があります. 固定ベッド反応器の幅と深さ (円筒形反応器の場合は半径) に沿って小さな変化がある場合, 入口から出口まで, 反応器の高さに沿った1Dモデルを使用してマクロモデルを記述できます. 2つの独立した空間変数, 1つは z 方向, もう1つは多孔質触媒粒子の半径 r を持つモデルが得られます. 上記のマイクロ反応器の場合, このような簡略化により, 高さに沿った平均濃度と反応物の総変換率について, より詳細なモデルと適切に一致します.

下の図は, 上でモデル化したケースとは異なるケースを示しています. ここでは, 反応器はメートルスケールで, 固定ベッドには何百万もの触媒粒子があります. この触媒は, これまで研究したケースよりも活性が低くなります. この図の固定ベッド反応器は, 入口ノズル (赤) が反応器内の濃度分布に影響を与えるため, 1Dモデルで簡略化することはできません. この場合, モデルはマクロスケールで3Dであり, 粒子半径用の4番目の次元と時間用の5番目の独立変数が追加されています.

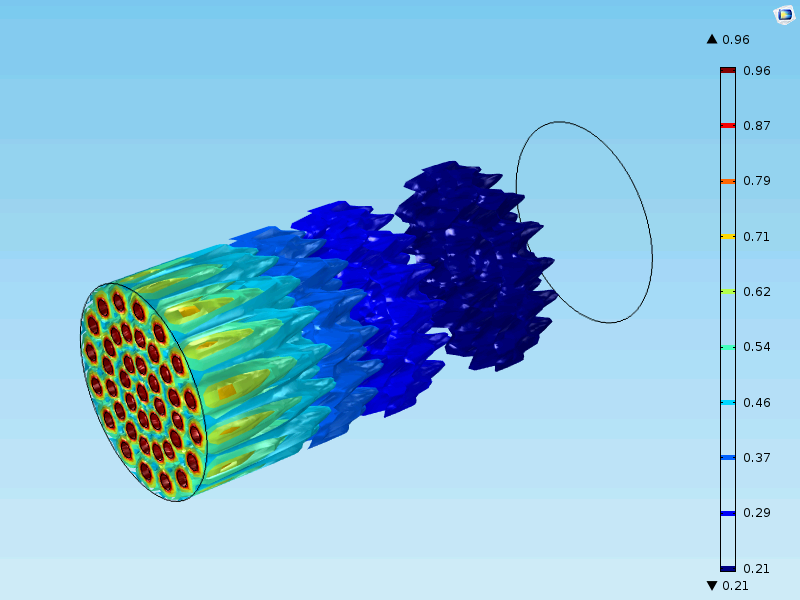
おわりに

輸送, 吸着, 反応, 脱着の各ステップを含む, かなり複雑な触媒の幾何学的構造を微視的レベルで記述できることが分かりました.

この記述は, 触媒粒子を多孔質の板として表す均質化を使用して, 微視的レベルで近似されました.

次のステップでは, 簡略化された粒子モデルを使用して多数の粒子をモデル化しましたが, 各粒子の位置と形状を詳細に記述すると, 粒子の内部のみが簡略化されました.

その後, 粒子の数も大きくなりすぎたため, マクロ的な反応器レベルで固定ベッド領域も均質化しました.

均質化と近似の手順に従うことで, ミクロレベルの粒子からマクロレベルの反応器まで, 触媒を詳細に設計し, この設計が反応器全体の性能に与える影響を研究することができます. さらに, この方法論は “逆” にも使用できます. つまり, マクロレベルの操作がミクロレベルの操作条件にどのように影響するかを研究し, 反応器内のさまざまな位置で関連する操作条件に合わせて触媒と床の設計を適応させることができます.