
Lightness by Design のゲストブロガー Björn Fallqvist が, 熱機械疲労を分析するためのさまざまな考慮事項とアプローチについて説明します.
このブログでは, 熱機械疲労を解析するための COMSOL Multiphysics® ソフトウェアの関連材料モデルを解析します. 熱機械疲労試験の実験データと, 参照文献の材料パラメーターを使用します. 次に, 高温で動作していると想定される圧力容器を解析し, 非線形連続疲労損傷モデルを使用して疲労寿命を評価します.
なぜ熱機械疲労を解析するのか
多くのアプリケーションでは, 従来の等温疲労解析では不十分です. 部材は高温で動作したり, 高温間を循環したりするため, 材料の挙動が室温とは大きく異なるからです. このようなアプリケーションの代表的な例としては, タービンや発電所の部材が挙げられます.
従来の疲労解析, 特に高サイクル疲労 (HCF) では, 高温による影響は直接考慮されません. HCF 領域では, 荷重は低く, クリープなどの影響は無視できると想定されます. 温度上昇による疲労強度の低下を考慮するために, S-N 曲線の縮小が行われることもあります. ただし, これは, 熱機械疲労と呼ばれる, 温度と荷重を同時に循環させる影響を考慮していません. この温度変化の影響は, 特に低サイクル疲労 (LCF) 領域で重要であり, この領域では, 主に弾塑性およびクリープの材料特性の変化など, 複数の側面を考慮する必要があります.
高温での疲労能力を評価する 1 つの方法は, いくつかの温度で安定した (多くの場合, 寿命の中間の) 試験片の応力 – ひずみ曲線を使用して, 応力またはひずみの振幅を取得し, 非線形応力 – ひずみ曲線を支配する硬化パラメーターを決定することです. その後, 理論的には, 適用された荷重と温度の特定の組み合わせで実験を行い, 実験結果から疲労寿命を推定することができます. ただし, 熱機械疲労試験は比較的時間がかかり, コストもかかります. 高温での疲労能力を評価するより便利な方法は, 応力レベルと破損までのサイクルの関係を表す解析式を使用し, それを温度で補正することです.
熱機械疲労試験
熱機械疲労試験では, 通常, 試験片は周期的なひずみと周期的な温度に同時にさらされます. これは, 同位相 (IP) または異位相 (OOP) のいずれかです. 前者の場合, 最大引張荷重は最高温度と同時に発生し, 後者の場合, 最大引張荷重は最低温度で発生します.
このブログの実験結果との比較のために, 参考文献 1 を参照します. この文献では, P91 (一般的な発電所用鋼) の熱機械疲労が解析されています. 応力-ひずみ曲線が取得され, 材料モデル パラメーターは 参考文献 2 から取得されました. 参照されている作業では, 統合モデル (つまり, 粘塑性ひずみが塑性成分とクリープ成分の両方で構成されている) が使用されていることに注意してください. ただし, これはモデルのクリープ部分の値にのみ影響します.
熱機械疲労解析のための材料モデル
温度の関数としての材料モデルパラメーター(参考文献 2)は以下のように指定されます. :
| Temp [°C] | E [MPa] | k [MPa] | Q [MPa] | b [-] | a1 [MPa] | C1 [-] | a2 [MPa] | C2 [-] | Z [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 150.0 | 2350.0 | 120.0 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 98.5 | 2191.6 | 104.7 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 52.0 | 2055.0 | 463.0 | 463.0 | 1750 | 2.7 |
表 1. 参考文献からの材料パラメーター.
パラメーターa と C は非線形移動硬化モデルに関連し, E は弾性係数, k は初期降伏応力, Q と b は等方性硬化パラメーター, Z と n は粘塑性流量の材料パラメーターです.
これらについては, 次のセクションで詳しく説明します. これらのパラメーターを組み合わせることで, 応力空間における降伏面の移動と拡張または収縮が決まります. モデル内のすべてのパラメーター値は, 温度間で補間されます. この実装については, 次のセクションで説明します.
粘塑性
速度依存効果は, 参考文献 5 に従って, 粘塑性ひずみテンソル \dot{\epsilon}_{vp} の速度に対する次の粘塑性 Chaboche 定式化を使用して考慮されます.
ここで, A は速度因子 (1/sと等しくなるように設定), F は降伏関数), nD は応力偏差のテンソル方向, n は材料パラメーター, \sigma_{ref} は参照応力値です.
調べてみると, COMSOL Multiphysicsパラメーターσrefとnは, それぞれ表1のZとnに対応することが分かります. 降伏関数Fは次のように定義されます.
ここで, R は降伏表面での増加, k は初期降伏応力, \sigma_b は移動硬化による背景応力テンソルです.
関数 φ はフォン・ミーゼス等価応力になるように選択されます.
等方硬化
降伏面サイズσyに対する等方硬化則(Voce)は次のように定義されます.
性ひずみにおける降伏面の大きさに対する飽和応力, β は材料パラメーター, \epsilon_{vp,e} は等価粘塑性ひずみです.
この定式化では, 飽和応力値に応じて, 塑性ひずみの増加に伴って降伏面が拡大または縮小することがあります. COMSOL Multiphysics パラメーター σsat と β は, それぞれ 表 1 の Q と b に対応します.
移動硬化
選択された非線移動硬化則はChaboche硬化であり, 背景応力テンソルはArmstrong–Frederick非線形硬化項のj個の重ね合わせたブランチで構成されます:
初期の移動硬化係数を持つ最初の項は, この解析では無視されます. 参考文献 1, 2 で使用されている定式化と比較すると, COMSOL Multiphysics® の 2 つのブランチの硬化パラメーター C と γ は, それぞれ Ca と C です.
クリープ
前述のように, 参照された論文では, 著者らは統一された粘塑性モデルを使用し, 粘性応力は直接定義されています. COMSOL Multiphysics®では, クリープひずみの速度に次のNortonクリープモデルを使用しています:
ここで, Ac は速度テンソル, σeff は等価応力, σref は参照応力値 (1 MPa に設定), nc は材料パラメーターです. これらのパラメーターの値は, 参考文献 4 から取得されました.
COMSOL Multiphysics® で使用する材料パラメーターの概要
解析に使用した材料パラメーターを以下にまとめます. パラメーター名はほとんどの場合, COMSOL Multiphysics® のラベルを反映するように変更されていることに注意してください. また, 定数 C の定義は参照文献で使用されているものと異なるため, 異なる値になります.
| Temp [°C] | E [MPa] | \sigma_{ys0} [MPa] | \sigma_{sat} [MPa] | β [-] | C_1 [MPa] | \gamma_1 [-] | C_2 [MPa] | \gamma_2 [-] | \sigma_{ref,vp} [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 352,500 | 2350.0 | 810,000 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 215,870 | 2191.6 | 863,810 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 106,860 | 2055.0 | 810,250 | 463.0 | 1750 | 2.7 |
表 2. COMSOL Multiphysics® で使用する材料パラメーター.
クリープパラメーター A_c=2.462 \cdot 10^{-6}/s, \sigma_{ref,cr}=1 MPa, n_c=7.538 はすべての温度で同じであり, ポアソン比 0.3 および熱膨張係数 \alpha=14.5 \cdot 10^{-6}/^{\circ}C も同様でした. クリープパラメーターは 873 K で測定されましたが, 温度依存性も COMSOL Multiphysics® に含めることができることに注意してください.
非線形連続損傷疲労モデル
背景
疲労解析で使用する疲労モデルは, Chaboche が提案した非線形連続疲労損傷モデルです (参考文献 3). このモデルは, その使いやすさと, 低サイクル疲労と高サイクル疲労の両方 (鋼の場合) に有効であることから魅力的です. 簡単に言うと, 次の式の速度損傷方程式に基づいています.
サイクル数 N に対する損傷変数 D の速度は, 最大応力 \sigma_M, 平均応力 \bar\sigma, および現在の損傷に依存します. 関数 f の特定の選択により, (ここでは導出を省略) 破損までのサイクル数 NF の関係が得られます:
ここで, a と \beta_{fat} は材料パラメーター, \sigma_u は最大引張強度, \sigma_l は
に基づく平均応力の疲労限界 \bar\sigma です.
ここで, b_{fat} は材料パラメーターです.
最終的に, M\bar{(\sigma)} は次のように定義されます.
ここで, M_0 は材料パラメーターです.
熱機械疲労では, 温度Tが変化するため, サイクル中の有効温度(T*)は次のように計算できます.
基本的に, 有効温度 T* は, 極端な温度間の時間範囲 \Delta t にわたる平均サイクル数と同じサイクル数 NF が計算される温度とみなされます.
疲労データといくつかの仮定
室温では, P91 鋼の最大引張強度は 600 MPa (文献 7), 疲労限度は 文献 6 から引用した約 420 MPa で, さまざまな応力レベルでの破損までのサイクル数も示されています. これらを使用して, Chaboche 疲労モデル (図 1) で定義されている S-N 曲線の最小二乗近似を決定できます. ここで, 荷重比 R (R=\frac{\sigma_{min}}{\sigma_{max}}, 最小応力と最大応力の比) は R = -1, つまり \bar\sigma=0 です. パラメーター決定については, M\bar{(\sigma)}=M_0および\sigma_l(\bar\sigma)=\sigma_{l0}です.
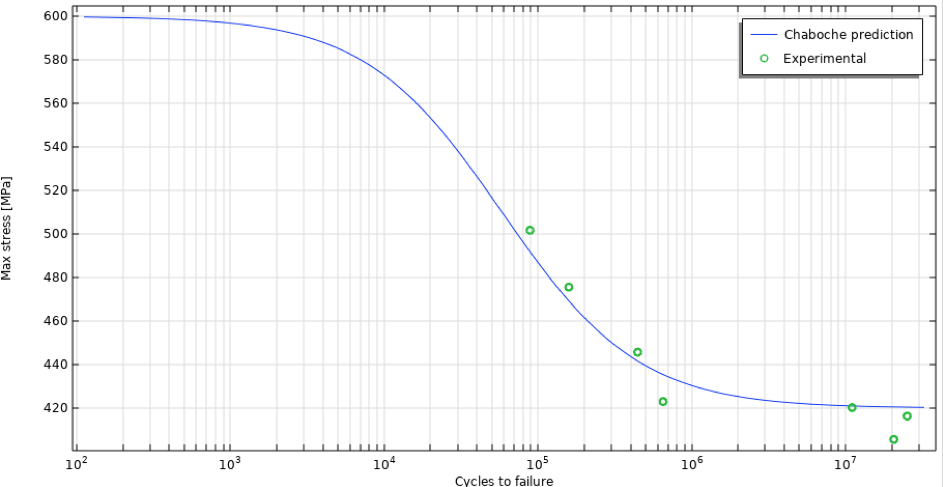
図 1. Chaboche 疲労モデルによって定義された S-N 曲線.
結果として得られるパラメーターは, a = 9 \cdot 10^{-6}, \beta_{fat}=0.287, M_0=54.3 MPa です.
理想的には, 曲線を完全に定義するには中間領域にさらに多くの点が必要ですが, 方法のデモンストレーションにはこれで十分です. 熱効果を考慮することが重要なので, S-N 曲線をスケーリングする必要があります. これを行うにはいくつかの方法がありますが, 最も適切なのは, さまざまな温度での曲線を使用し, 各温度での材料パラメーターを取得して, これらを補間することです. ただし, そのようなデータがない場合, 極限引張強度と疲労限界を, 参考文献 1 の図 3.24 で定義されている低減係数に従ってスケーリングすると便利です. 結果として得られる S-N 曲線を図 2 に示します. これらはすべて R = -1 の場合であることに注意してください.
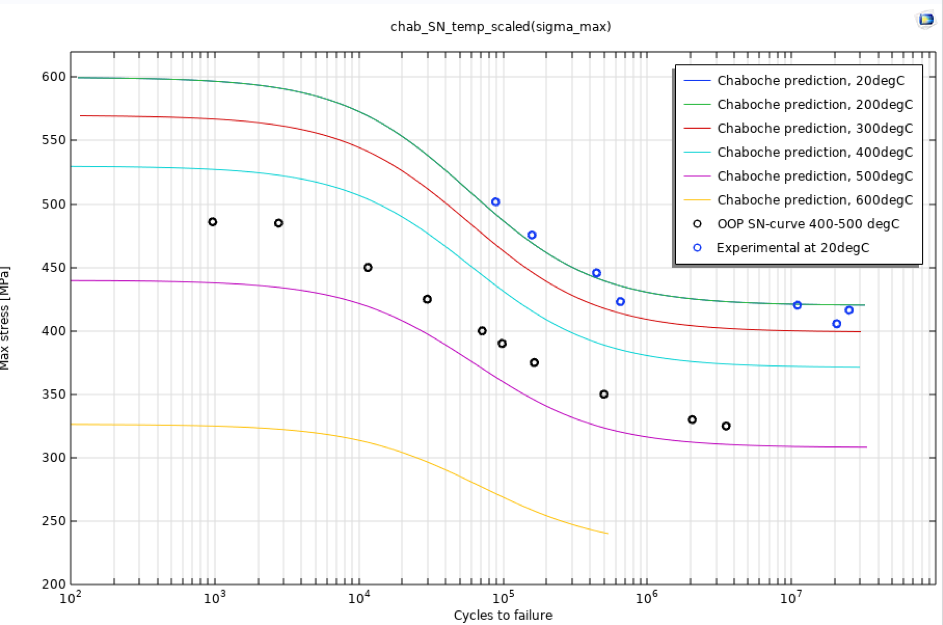
図2. 温度低下によるChaboche S-N曲線.
これらの曲線を温度に合わせてスケーリングする実装については, 次のセクションで説明します. 参考文献 2 の設定で定義されている, 400°C から 500°C の間の位相がずれた温度サイクルを想定して, 選択した数の応力レベルについて計算された破損サイクルも含まれています.
平均応力の影響を考慮する必要がある場合は, パラメーター b_{fat} が必要です. 必要な場合は, 平均応力に関する疲労限度の Goodman 減少が使用されます. つまり, \bar\sigma=\sigma_u, \sigma_l=0 の場合です. これにより, b_{fat}=0.0041/MPa になります.
計算モデル
背景: 実験的比較
実験的な熱機械的疲労試験 (等温および位相外れ) は, 参考文献 2 で実施されました. 単軸引張試験は, 等温および非等温条件の両方で高温で実施されました. 熱機械的疲労解析に必要な手順を定義するプロセスを示すために, 実験セットアップと試験手順が COMSOL Multiphysics® で再現されています. 公開された実験の結果が解析結果と比較されています.
背景: 疲労評価
試験片よりも現実的なケースを示すために, 周期的な温度と圧力負荷を受ける圧力容器の疲労解析が解析されます. 結果として生じる応力状態によって疲労計算の入力が定義され, 破損までのサイクル数が推定されます.
幾何モデル: 実験的比較
参考文献 2 には, 試験片の形状が示されています. 周期的な応力-ひずみ曲線を簡単に計算するには, 狭い領域の半分だけを軸対称モデルとしてモデル化すれば十分です. 図 3 を参照してください. 軸からのオフセットは, 試験片に穴があるために生じることに注意してください.
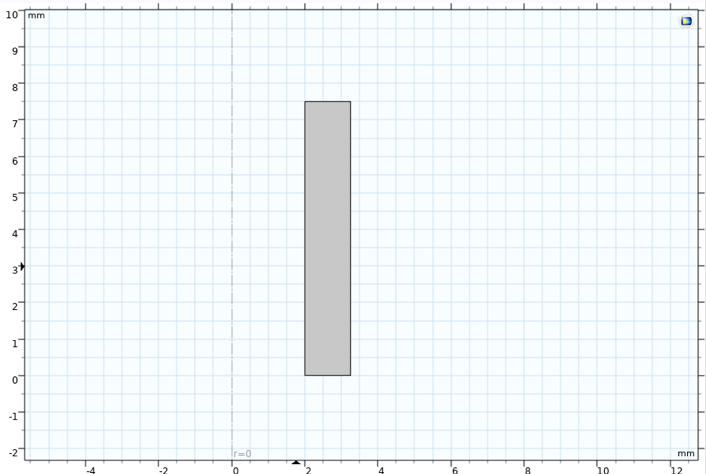
図 3. 試験片の軸対称モデル.
幾何モデル: 疲労評価
熱機械疲労の現実的なケースを表す圧力容器は, 全長 6000 mm, 内半径 950 mm, 厚さ 50 mm です. これは軸対称モデルとして簡単にモデル化できます. 図 4 を参照してください.
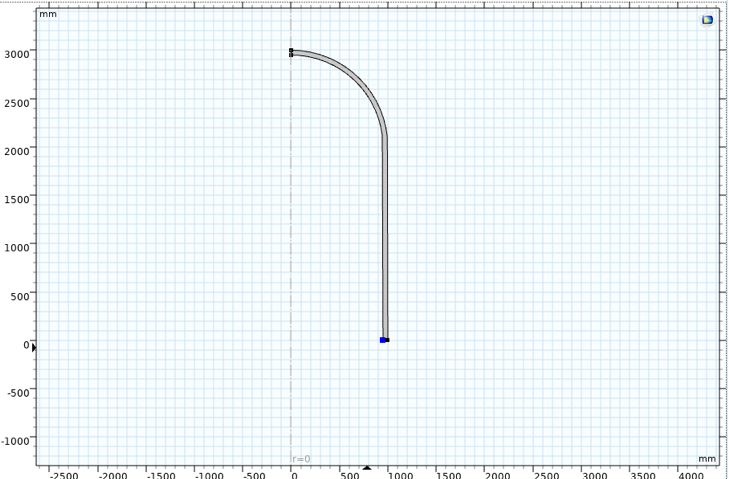
図4. 軸対称圧力容器モデル.
メッシュ: 実験的比較
非常に均一な荷重の場合, メッシュは非常に粗くなる可能性があります. ここでは, 図 5 に示すように, メッシュを自由三角形に設定し, 最大要素サイズを 0.75 mm に設定しています.
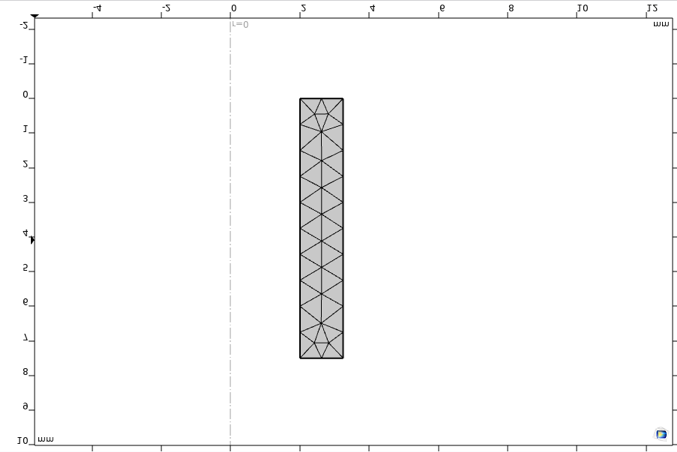
図5. 単軸試験片メッシュ.
メッシュ: 疲労評価
圧力容器モデルは, 図 6 に示すように, 最大メッシュ サイズ 50 mm の自由三角形メッシュでメッシュ化されています. 厚み方向に常に複数の要素が存在することが保証されていますが, このブログの説明目的上, これはあまり重要ではありません.
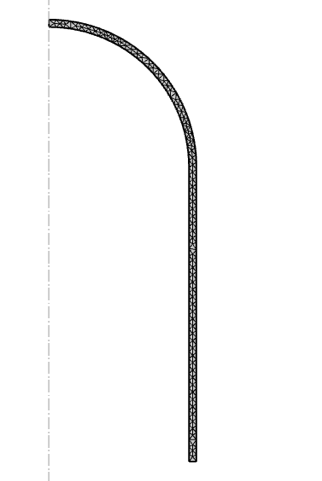
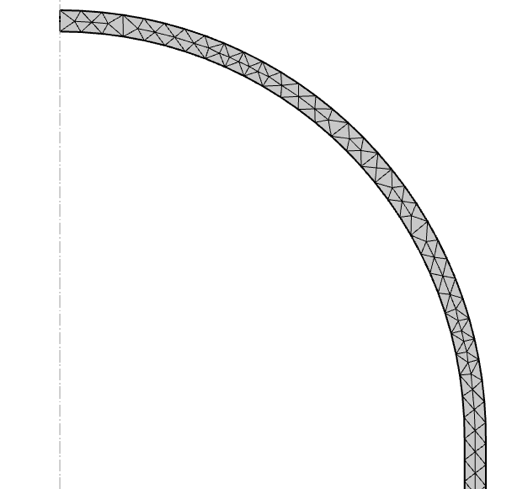
図6. 圧力容器のメッシュ.
フィジックス設定: 材料, 荷重, 境界条件 (実験との比較)
固体力学インターフェースは, 熱機械疲労解析に使用されます. まず, 材料を定義する必要があります. 前のセクションで説明した必要なモデルを有効にするには, 図 7 に示すように, 粘塑性とクリープを持つノードを追加します.
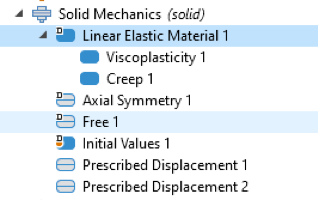
図7. 材料定義に必要なノード.
線形弾性, 粘塑性, およびクリープ ノードの場合, 次のセクションで例示するように, 適切な材料パラメーターが温度依存形式で入力されます.
モデルは軸対称なので, 必要な制約は軸方向のみです. z = 0 の下部境界は, z 方向に制約されます. ただし, 上部境界には, それぞれの荷重ケースで測定されたひずみに対応する変位が割り当てられます.
フィジックス設定: 材料, 荷重, 境界条件 (疲労評価)
圧力容器の場合, 材料の設定は同じです. 同様に, z = 0 の対称エッジは z 方向に固定されます. 圧力は内壁境界に適用されます. この圧力負荷は R = 0 負荷ケースで, 最大圧力は 170 bar です. 温度サイクルは実験比較よりも高い温度で行われ, 最高 (600°C) は 0 bar, 最低 (500°C) は 170 bar です. 負荷率は 5.67 bar/s です.
スタディ設定: 実験的比較
クリープおよび粘塑性材料モデルを利用するには, 時間依存のスタディが必要です.
等温テストでは, 初期サイクルが比較に使用されます. ひずみ速度が 0.1%/s の場合, 初期サイクル時間は 20 秒です. 出力時間は 2.5 秒に選択されています. 時間ステップは 0.25 秒で手動で設定されています.
非等温の場合, 比較には 50 サイクル目が使用されます. ひずみ速度が 0.033%/s の場合, 初期サイクル時間は 60 秒, 合計時間は 3000 秒です. 出力時間は 2.5 秒に選択され, 時間ステップは 1 秒に設定されています. 温度率は 3.33°C/s です.
スタディ設定: 疲労評価
圧力容器解析の場合, 荷重と温度率は非等温実験比較の場合と同じです. 出力と時間ステップの設定も同じです.
関数と変数の定義
熱機械疲労解析に適したモデルを構築すること自体は必ずしも複雑ではありませんが, 上記のフレームワークには多くの側面があります. まず, 温度と温度に関連する材料パラメーター, および荷重の一貫した変化のためのフレームワークが必要です. COMSOL Multiphysics® では, 関数と変数を使用することでこれを最も簡単に処理できます. このセクションでは, 非等温解析 (実験比較用) を使用してこの方法を概説します.
パラメーター
まず, 形状, 荷重, 材料クリープ, 材料疲労パラメータなど, 解の影響を受けないグローバルパラメーターを定義します (図 8 を参照).
図 8. グローバルパラメーター.
これで, 荷重の形状を決定する単純なスケーリング関数によって, 公称荷重値 (温度や変位など) を適用できます.
温度関数
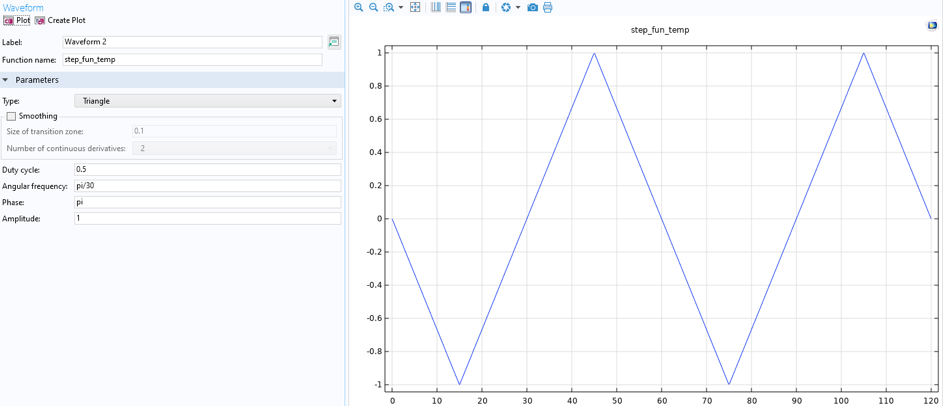
等温実験の場合, 温度は 400°C で一定です. 非等温実験の場合, 最小ひずみで最高温度 (500°C), 最大ひずみで最低温度 (400°C) の温度定義が必要です. この変化は, 波形と解析関数を作成することで得られます. 図 9 を参照してください.
図 9. 温度関数, 非等温荷重ケース.
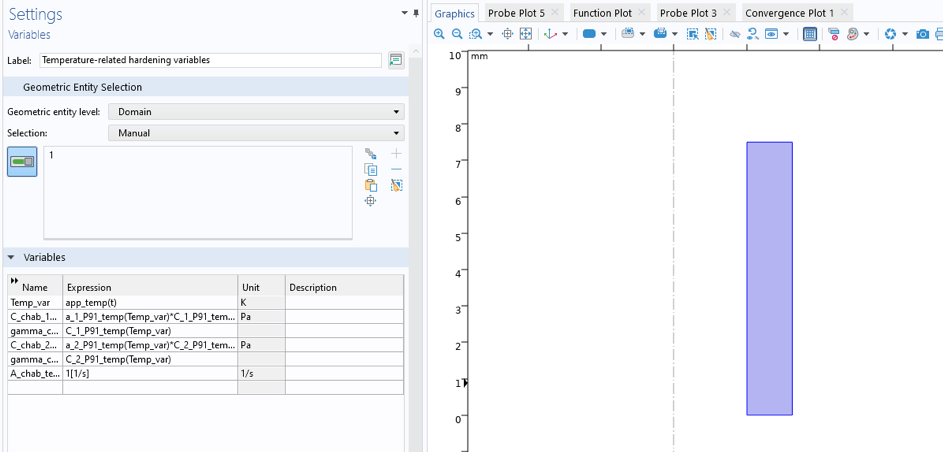
次に, 温度をモデルドメインの変数 (TempVar) として適用します (図 10 を参照).
図 10. ドメイン変数としての温度の定義.
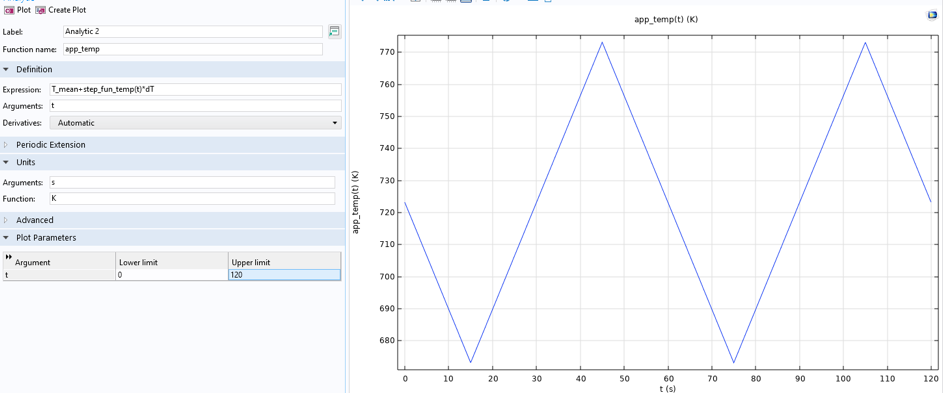
圧力容器の場合, 図 11 に示すように, 温度は 500°C から 600°C の間で循環します. 温度も同様に, モデル内でドメイン変数として表されます.
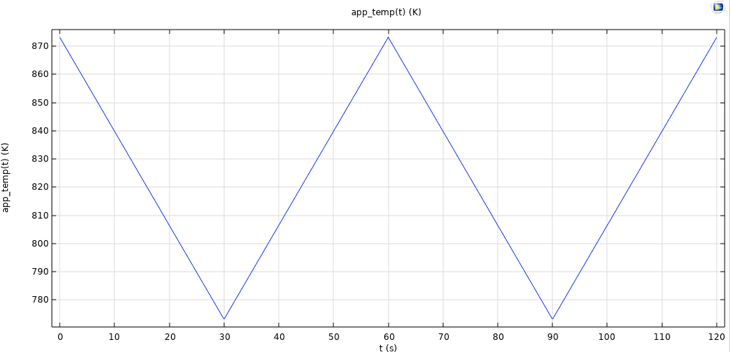
図11. 圧力容器ケースの温度関数.
導入された温度変数は, 材料特性の変化を決定するために使用できますが, 熱膨張は考慮されません. 実験の場合, 総ひずみ (機械的および熱的) は機械制御されるため, これはあまり重要ではありませんが, 一般的には, 熱膨張による熱ひずみを考慮する必要があります. これを行うには, 固体の伝熱フィジックスインターフェースを含め, ポイントごとの拘束を追加して, 必要に応じて温度を適用できます. 図 12 を参照してください.
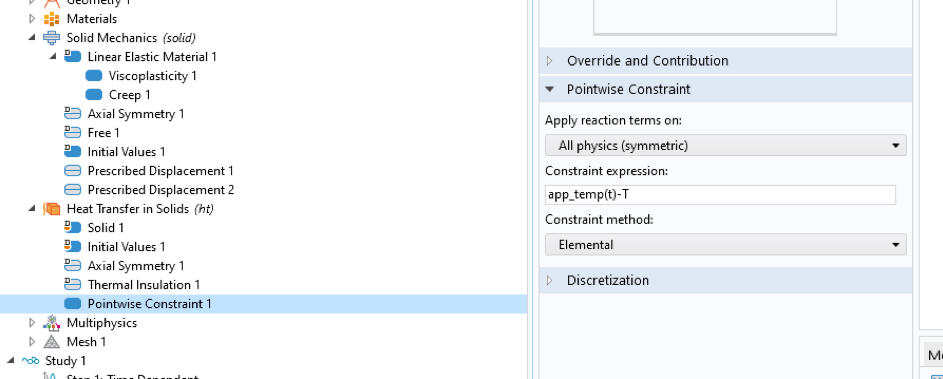
図12. 固体の伝熱フィジックスインターフェース.
もちろん, 均一な温度分布は現実的ではありません. 適切な熱伝達解析を使用して温度場を取得することもできます. 熱伝達解析では, 基準温度を指定する必要があります. これは, 熱ひずみがゼロになる温度, つまり (熱) 応力のない構成です. これは通常, 室温ですが, 疲労解析では, 通常, 荷重範囲と平均が重要です. したがって, 解析では, 基準温度はサイクルの最大温度である 873 K に設定されます.
荷重関数
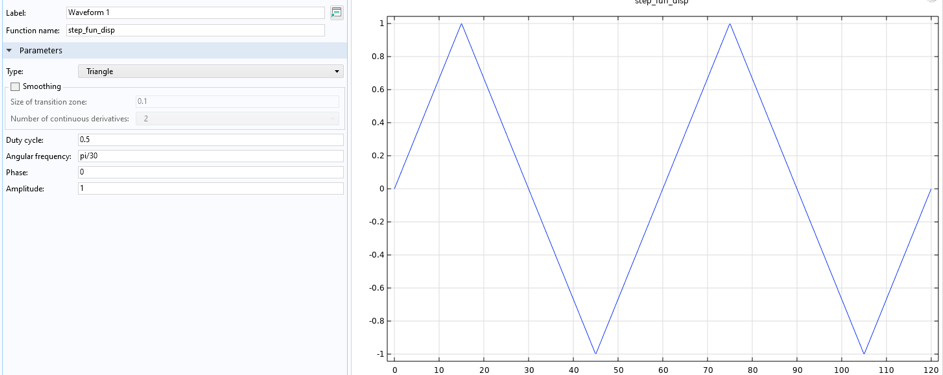
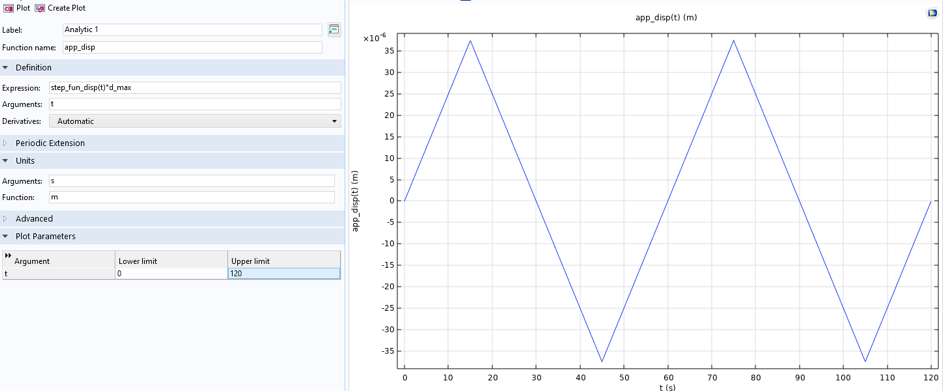
温度の定義と同様に, 荷重 (この実験ケースでは変位) も, 波形と解析の 2 つの別個の関数によって定義されます (図 13 を参照).
図13. 荷重関数, 非等温荷重ケース.
この特定の数値は, 非等温実験ケースに特有のものです. 非等温ケースと等温ケースでは, ひずみ速度が異なります. 後者の場合, ひずみ速度は 0.1%/s で, 前者の場合, ひずみ速度は 0.033%/s で, それぞれ 7.5 µm/s と 2.5 µm/s の変位速度に相当します. サイクル中の最大ひずみは 0.5% で, これは合計 37.5 µm の端部変位を表します. これは, 試験片の狭い領域 7.5 mm にわたってひずみを測定するゲージ長に関係しています. 半分の長さのモデルが使用されていることに注意してください. 狭い領域の全長は 15 mm です.
圧力容器の場合, 図 14 に示すように, ピーク圧力が 170 bar, 負荷速度が 5.67 bar/s の負荷関数が定義されます.
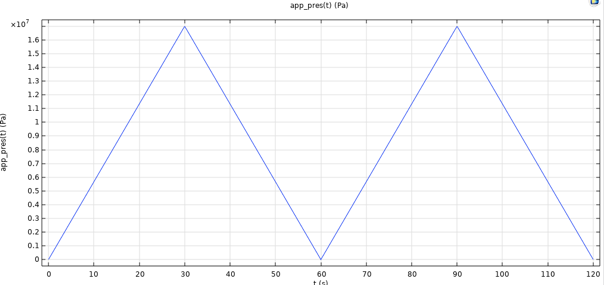
図14. 荷重関数, 圧力容器ケース.
材料パラメーター関数
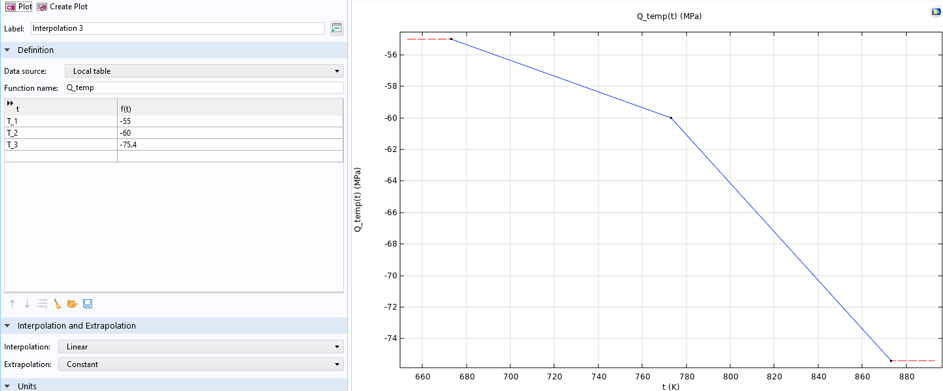
材料パラメーターは温度依存性を持つ必要があり, これは指定された温度での既知のパラメーター値を持つ補間関数を作成することによって最も簡単に取得できます. たとえば, σsat は図 15 のように定義されます.
図15. 温度依存σsatの関数の定義.
次に, 作成された温度変数を引数として使用して, この関数を呼び出すことにより, 温度依存の材料パラメータが適切に計算されます. これは, 図 16 に上記のパラメーターの例として示されています (図 9 を参照). 当然, 固体の熱伝達フィジックスインターフェースからの従属変数 T も引数として使用可能です.
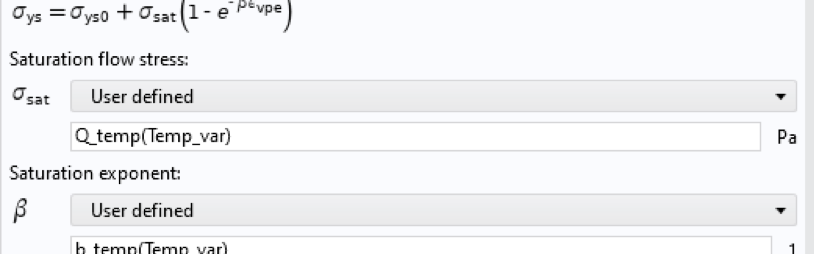
図 16. 材料パラメーターの定義で温度変数を呼び出す.
温度に応じて極限引張強度と疲労限度をスケーリングする手順は, 上で概説したものと似ていますが, 室温での基準値は, 無次元の減少係数でスケーリングされます (極限強度と疲労強度の両方をスケーリングするため). Chaboche S-N 曲線 (図 1 および図 2 を参照) を定義する解析関数の式は, 図 17 に示されており, ここでは最大応力の関数として室温 (293 K) で定義されています.
図 17. Chaboche S-N 曲線の解析関数.
スケーリング関数 UTS_temp_scaling は, 図 18 に示すように定義されます.

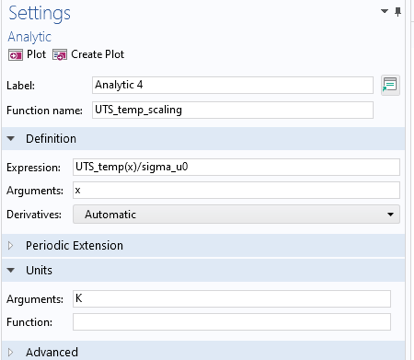
図18. 極限引張強度のスケーリング関数.
結果: 実験的比較
最初の Piola-Kirchhoff 応力の平均の境界プローブが, 変位が規定されているモデルの上部に作成されました. これが抽出され, 適用されたひずみの関数としてプロットされ, 周期的な応力 – ひずみ曲線が得られました.
等温試験
初期の周期的応力-ひずみ曲線を図19に示します.
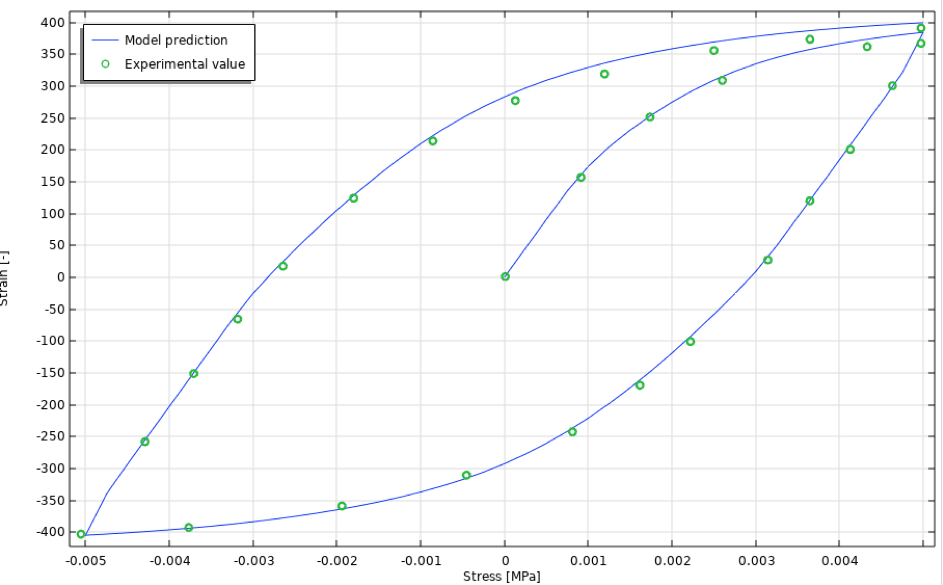
図19. 等温の場合の初期繰返し応力-ひずみ曲線.
予想どおり, モデルは初期の周期的応力-ひずみ曲線をうまく予測しているようです.
非等温試験
非等温周期応力-ひずみ曲線を図 20 に示します.
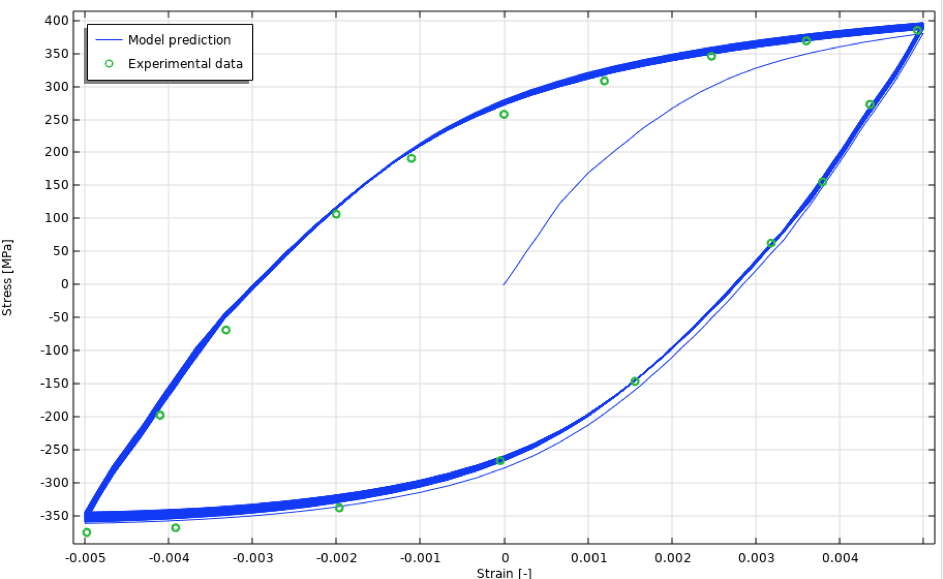
図 20. 非等温ケースにおける周期的応力-ひずみ曲線.
分離された50回目の繰り返し応力-ひずみ曲線を図21に示します.
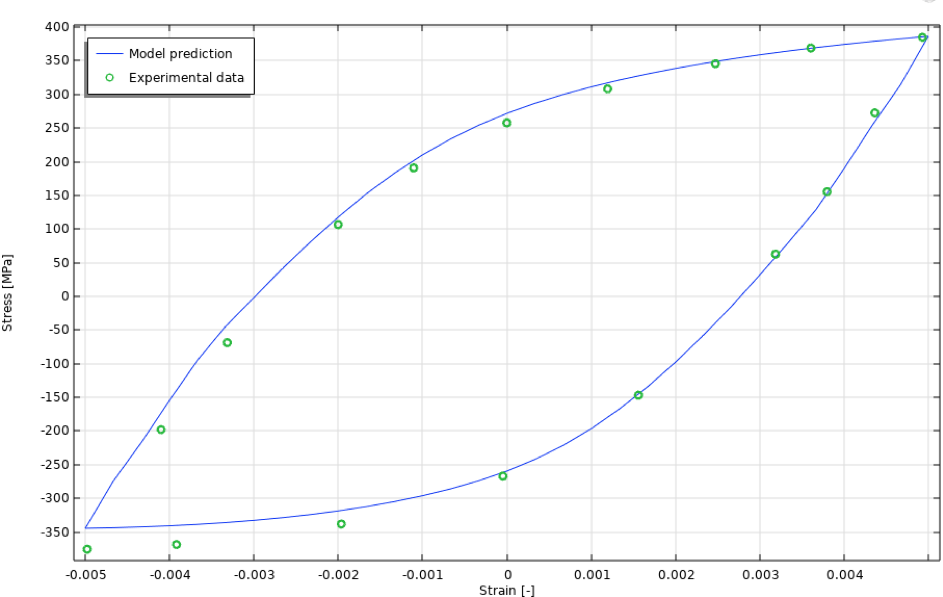
図21. 非等温ケースの50回目の繰り返し応力-ひずみ曲線.
結果: 疲労評価
応力とひずみ
50 回目サイクルの最大荷重時 (2970 秒) と除荷後 (3000 秒) のフォンミーゼス応力を図 22 に示します.
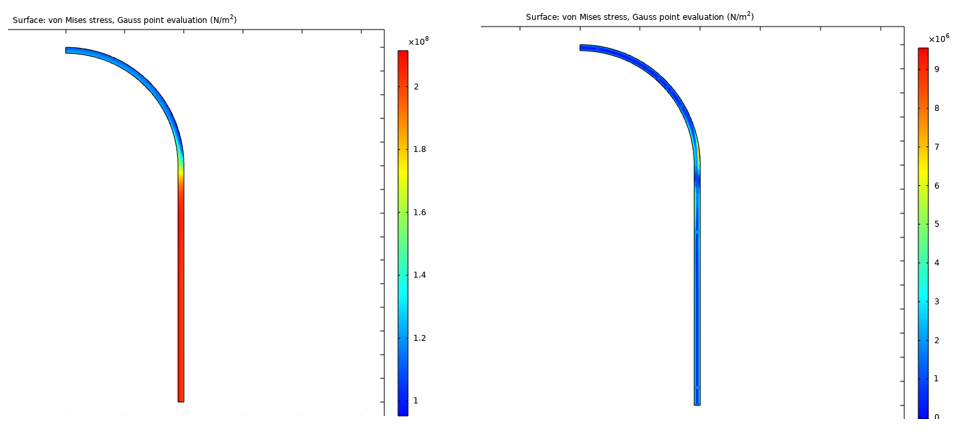
図22. 50サイクル目における最大荷重時(左)と除荷後(右)のフォン・ミーゼス応力.
50 回目サイクル後の等価粘塑性ひずみとクリープひずみを図 23 に示します.
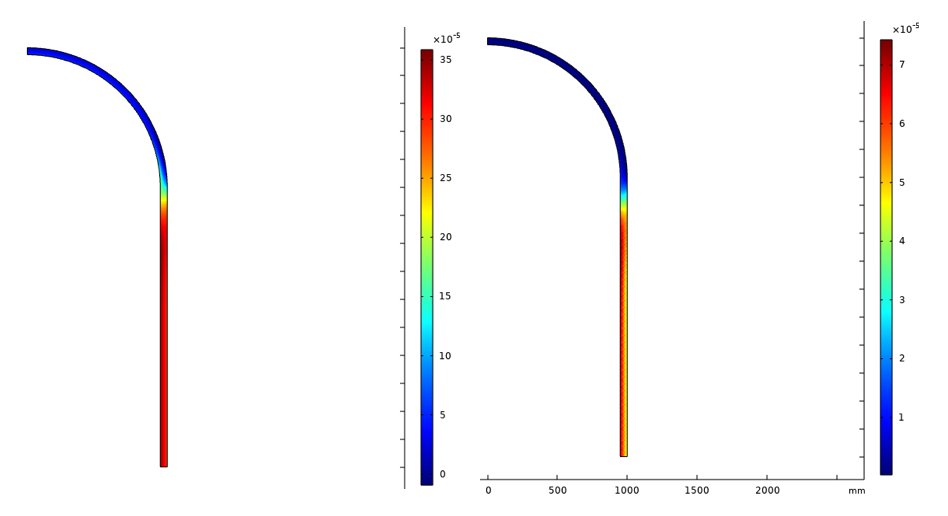
図 23. 50 回目サイクル後の等価粘塑性ひずみ (左) とクリープひずみ (右).
非対称応力サイクルの典型的な動作はラチェットであり, 残留ひずみがサイクルごとに増加します. 非線形移動硬化モデルはこれを考慮します. 通常, 平均応力が高い負荷サイクルはラチェットひずみを増加させる傾向があり, 平均応力が低いとラチェットひずみは時間の経過とともに安定します. 破損までの各サイクルを必ずしも計算せずに疲労サイクル数を推定するには (次のセクションを参照), 安定した応力ひずみサイクルを取得する必要があります. 圧力容器の最大等価偏差ひずみに対する最大フォン・ミーゼス応力をプロットすると, 図 24 の 2 つの極端なケースのラチェットひずみが模式的に表示されます.
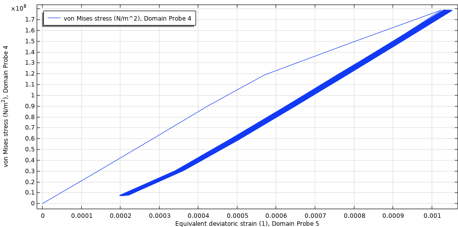
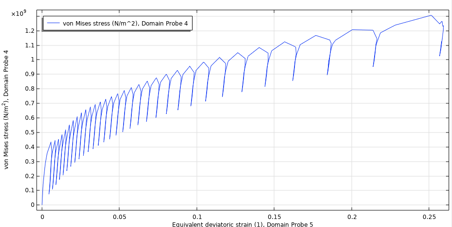
図24. 低平均応力 – 最大圧力100バール(左)と高平均応力 – 最大圧力240バール(右)のラチェットひずみ. どちらの場合もR = 0の荷重です.
平均応力が低い場合, サイクルはほぼ即座に安定します. 平均応力が高い場合, ラチェットひずみはサイクルごとに増加します. ここで検討した負荷ケースでは, 最大圧力 170 bar, つまり最初の 50 サイクルのラチェット動作が, 図 25 の右下モデルコーナーに抽出されて示されています. 保守的に, 最大ドメイン値を抽出することもできます.
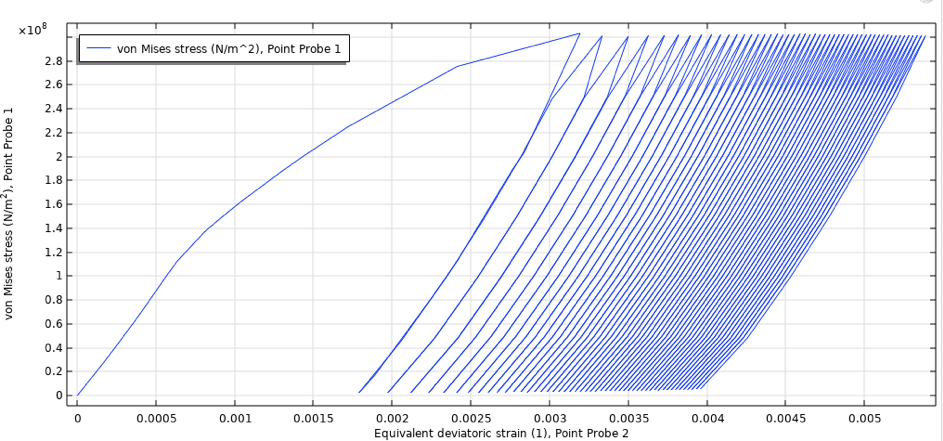
図 25. 圧力容器の応力-ひずみ挙動, 最大圧力 170 bar, 500°C ~ 600°C 間の位相外れサイクル.
各サイクルごとにラチェットひずみが明確に減少し, 応力-ひずみ曲線は 50 サイクル後に安定したと見なすことができます.
計算された破壊までのサイクル
前のセクションで定義した式を使用して, 部材の疲労寿命を推定する方法がいくつかあります. 累積損傷は, まず次の式を満たす有効温度T*を見つけることによって, 各サイクルごとに計算できます.
サイクル中の損傷の進行は次のように計算できます.
次に, 各サイクルの損傷を合計して, 総損傷を取得します. これらが代表的な負荷サイクルである場合, 破損 (D = 1) までのそのようなシーケンスの数を取得できます. また, 各サイクルの損傷を単純に計算して合計し, D = 1 になるまで解析を実行することも可能です. これらのアプローチは, 各サイクルで計算された変数を定義および評価するためのフレームワークを必要とするため, 面倒な場合があります. また, 部材を破損するまで解析するには, 通常, 低サイクル疲労の場合でも, 数百から数千に及ぶ計算サイクルが必要です. 大規模なモデルの場合, これは通常実行可能ではありません.
しかし, このブログの例のように, 部材が単一のタイプの負荷/温度サイクルにさらされる場合, 故障までのサイクル数は次のように解析的に計算できます.
その後は, 安定したサイクルの平均応力と最大応力を計算し, 上記の式を評価するだけです. まず, 疲労のリスクがあるポイントの応力-ひずみプロットを時間の経過と共に可視化して, 安定したサイクルを確保する必要があります. 図 25 によると, 応力-ひずみサイクルは安定しているように見えます.
平均応力は, 図 26 に従って最大応力に対する点解プローブの時間平均演算子の導出値として149.7 MPaと計算されます.
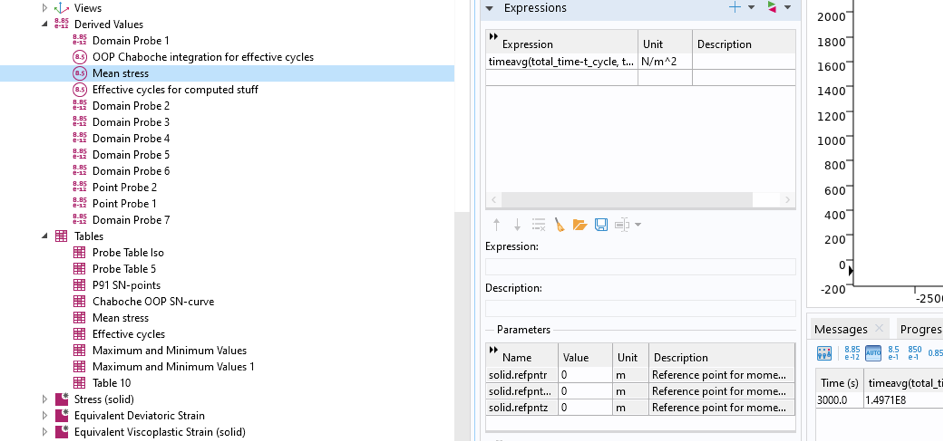
図 26. 安定化サイクルの平均応力の計算.
サイクル数 N_{F}^{*} の解析式は, 図 27 に従って, 時間, 最大応力, 平均応力の関数として定義されます. この式は, 時間積分で使用する必要があるため, 図 17 の一般的な式とは異なります.
図27. 時間, 最大応力, 平均応力の関数として計算された破壊までのサイクル数の定義.
これは, 図 28 に示すように, 故障までのサイクル数を導出値として計算するために使用されます. 最大応力は, プローブ テーブルから最も簡単に313 MPaと取得できます.
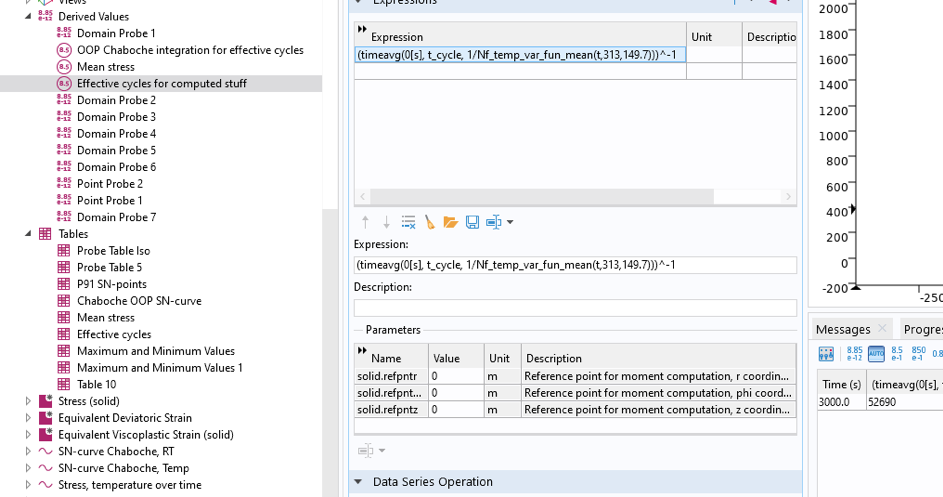
図 28. グローバル評価ノードを使用した破壊までのサイクル数の計算.
計算された故障までのサイクル数は 52,690 です.
結論と考察
熱機械的疲労は多くの用途において極めて重要です. 排出量を削減するために, これまで以上に高温で稼働する発電所はその一例にすぎません. 高温と高負荷では, 温度に依存する材料特性, クリープ, 熱ひずみがすべて熱機械的疲労に影響します.
COMSOL Multiphysics® を使用すると, このブログで説明されている非線形材料モデルを使用してこれらの現象を組み込むことができます. 特に重要なのは, 時間の経過に伴う周期的な応力-ひずみ曲線の挙動を制御する硬化パラメーターです. 温度のユーザー関数を定義し, 材料特性を温度依存にする機能を使用すると, よく知られている Chaboche 疲労モデルを使用して, 熱負荷と機械負荷が同時にかかった部材の疲労破損までのサイクル数を推定できます. 負荷/温度サイクルが部材の寿命全体にわたって同一である場合, 解析式を使用してこれを簡単に行うことができます.
より複雑な荷重履歴の場合, 各サイクルで, このサイクルの熱荷重と機械的荷重を表す有効な温度を見つける必要があります. 次に, これを使用して, 関数 f(\sigma_M, \bar\sigma, D, T^*) で使用される関連する材料パラメーター (このブログでは, 極限引張強度と疲労寿命) を適切にスケーリングし, この特定のサイクルの損傷を計算します. この増分プロセスによって損傷が蓄積され, D = 1 の場合, 疲労破壊が発生したと想定されます. 最大で数千サイクルを超えるサイクルがカウントされるものについては, 必要な時間が長すぎるため, これは実際には実行可能なアプローチではありません. 可能であれば, 代表的なサイクルのシーケンス (荷重ブロック) を識別する方が適切なアプローチです.
いくつかの点に注意する必要があります. 参照された記事で使用されている材料モデルは, Chaboche 粘塑性硬化モデルで使用されるのと同じ材料パラメーターに依存して粘性応力が解に追加される, 統一された Chaboche 粘塑性モデルを使用しています. 統一された粘塑性モデルは COMSOL Multiphysics® には実装されておらず, このブログでは代わりに Norton クリープ則が使用されています. 計算された COMSOL Multiphysics の結果は, 実験データとよく一致しています. また, フォン・ミーゼス応力を疲労応力として使用することは, 静水圧荷重に依存しないことを考えると, 技術的には適切な選択ではない可能性があります. たとえば, 荷重は比例し, 主応力方向の方向は一定であると想定できるため, 正弦基準の方が適切である可能性があります. ただし, このブログでは, 正弦基準を実装してもあまりメリットはありません.
著者紹介
Björn Fallqvist 氏は, 数値解析に基づく製品開発に携わる Lightness by Design のコンサルタントです. 2016 年に英国王立工科大学で博士号を取得し, 生体細胞の機械的挙動を捉える構成モデルの開発に取り組んでいます. 彼の主な職業的関心と専門分野は, 材料特性評価と, さまざまな材料モデルを使用して物理現象を捉える分野です.
参考文献
- S. Natesan et al., Preliminary Materials Selection Issues for. s.l. : Argonne National Laboratory, 2006.
- C.J. Hyde et al., “Thermo-mechanical fatigue testing and simulation using a viscoplasticity model for a P91 steel”, Computational materials science, no. 56, 2012.
- J.L. Chaboche and P.M. Lesne, “A non-linear continuous fatigue damage model”, Fatigue fracture and Engineering Materials Structures, vol. 11, no. 1, pp. 1&ndash17, 1987.
- A.A. Saad et al., “Thermal-mechanical fatigue simulation of a P91 steel in a temperature range of 400-600C”, Materials at high temperatures, no. 28, 2011.
- COMSOL Multiphysics®, Structural Mechanics Module User’s Guide.
- X. Feng et al., “Determination of creep properties of P91 by small punch testing”, Materials at high temperatures, vol. 32, no. 4, 2015.
- Y. Gorash and D. MacKenzie, Open Eng, vol. 7, 2017.




コメント (0)