
前回, COMSOL Multiphysics®ソフトウェアのフラウンホーファー回折モデルで長方形開口のフーリエ変換を計算する方法を学びました. その例では, 開口は解析関数として与えられました. フーリエ変換のソースデータが計算された解である場合, 手順は少し異なります. このブログでは, フレネルレンズの電磁シミュレーションを使用して計算された解のフーリエ変換を実装する方法を学習します.
フーリエ光学によるフーリエ変換
シミュレーションにフーリエ変換を実装すると, フーリエ光学, 信号処理(周波数パターン抽出で使用), および画像処理によるノイズリダクションとフィルタリングに役立ちます. フーリエ光学では, フレネル近似は, 回折開口の近くの場を計算するために使用される近似方法の1つです. 回折開口が (x,y)のz=0平面にあるとします. 回折開口からの距離z=fにある(u,v)平面の回折電場は次のように計算されます.
ここで, \lambdaは波長であり, E(x,y,0), \ E(u,v,f)はそれぞれ(x,y)平面と(u,v)Q平面での電場を表します. (詳細については, 参考文献1を参照してください. )
この近似式では, 回折場は, 入射場に2次位相関数を乗じてフーリエ変換することによって計算されます{\rm exp}\{-i\pi (x^2+y^2)/(\lambda f)\}.
位相関数の符号の規則は, 場の時間依存性の符号の規則に従う必要があります. COMSOL Multiphysicsでは, 電磁界の時間依存性は {\rm exp}(+i\omega t) の形式です. したがって, 2次位相関数の符号は負です.
フレネルレンズ
それでは, フレネルレンズの例を見てみましょう. フレネルレンズは, 曲面部分を除いて通常の平凸レンズであり, レンズの高さに沿って m \lambda/(n-1)の倍数ごとに平らな側に折りたたまれます. ここで, mは整数, nはレンズ材料の屈折率です. これはmth次フレネルレンズと呼ばれます.
光の伝播方向に沿ったこの特定の高さによる表面のシフトは, 2m \piによる光の位相のみを変更します(大まかに言えば, 近軸近似の下で). このため, 折りたたまれたレンズは基本的に遠方場で同じ波面を再現し, 元の折りたたまれていないレンズのように動作します. 主な違いは回折効果です. 通常のレンズは基本的に回折を示しませんが(開口によるケラレがない場合), フレネルレンズは, 表面の不連続性と内部反射のために, メインスポットの周囲に常に小さな回折パターンを示します.
フレネルレンズをデジタルで設計する場合, レンズの表面は個別の層で構成され, 階段のような外観になります. これはマルチレベルフレネルレンズと呼ばれます. ステップの平坦な部分のため, マルチレベルフレネルレンズの回折パターンには, 通常, 高次の回折に加えて, 0次の背景光が含まれます.

ボストンの灯台にあるフレネルレンズ. Manfred Schmidt氏による画像—自己の作品. ウィキメディアコモンズを介して, CC BY-SA4.0の下でライセンス供与されています.
なぜ, フレネルレンズを例に挙げているのでしょうか? その理由は, 灯台がフレネルレンズを使用している理由と似ています. フレネルレンズは高さ方向に折りたたまれています m \lambda/(n-1). それは非常に薄く, 重量と体積を少なくすることができるので, これは, 従来の屈折タイプの大きくて重くて厚いレンズと比べて, 灯台に使うレンズとして有利です. 同様に, 私たちの目的においては, フレネルレンズは要素数が管理可能であるため, COMSOL Multiphysics とアドオンの 波動光学モジュールでのシミュレーションが容易になります
COMSOL Multiphysics® における収束フレネルレンズのモデリング
次の図は, フーリエ変換を実装する方法を示すためにシミュレートしようとしている光学レイアウトを示しています. これは, 波動光学 (周波数領域)インターフェースによって求解される計算された解に適用されます.
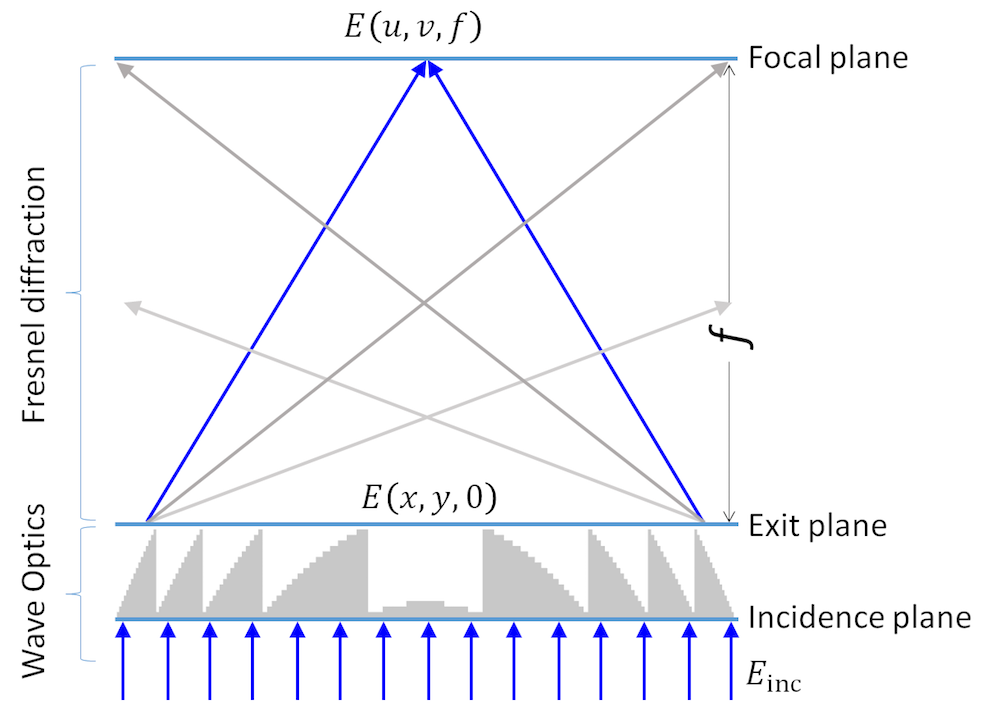
16レベル収束フレネルレンズモデル.
これは, 16レベルでデジタル化された表面を備えた1次フレネルレンズです. 平面波E_{\rm inc}が入射面に入射します. z=0の出口面では, 場はフレネルレンズによって回折されてE(x,y,0)になります.
このプロセスは, 波動光学 (周波数領域)インターフェースによって簡単にモデル化およびシミュレーションできます. 次に, 前述のように, フレネル近似でフーリエ変換を適用することにより, z=fの焦点面での場E(u,v,f)を計算します.
以下の図は, ドメイン内(上)と出口面に対応する境界上(下)の電場成分を使用した計算結果です. ジオメトリは垂直軸に合わせて描画されていないことに注意してください. 中心から, そして鋸歯の間のすべての空気ギャップから, 正に湾曲した波面をはっきりと見ることができます. レンズ表面からの反射により, ドメイン場の結果に小さな干渉が発生し, 境界場の結果にリップルが発生することに注意してください. これは, 反射防止膜がモデル化されていないためです.

フレネルレンズと周囲の空気領域で計算された電場成分(縦軸は原寸に比例していません).
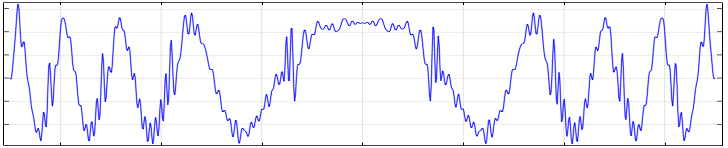
出口面で計算された電場成分.
計算された解からのフーリエ変換の実装
フーリエ変換に移りましょう. 前のブログの解析関数の例では, 2つのデータセットを準備しました. 1つはソース空間用で, もう1つはフーリエ空間用です. データセットの設定ウィンドウで定義されたパラメーター名は, ソース平面の空間座標(u,v)と画像平面の空間座標(x,y)でした.
今日の例では, ソース空間は Study 1/Solution 1 (sol1){dset1}にすでに計算された解とともに作成されています. 必要なのは, フーリエ空間のパラメーターを使用して1次元データセットGrid1D {grid1}を作成することだけです. つまり, 焦点面の空間座標uです. 次に, 次の図に示すように, それをソースデータセットに関連付けます. そして, 出口平面に積分演算子intop1を定義します.
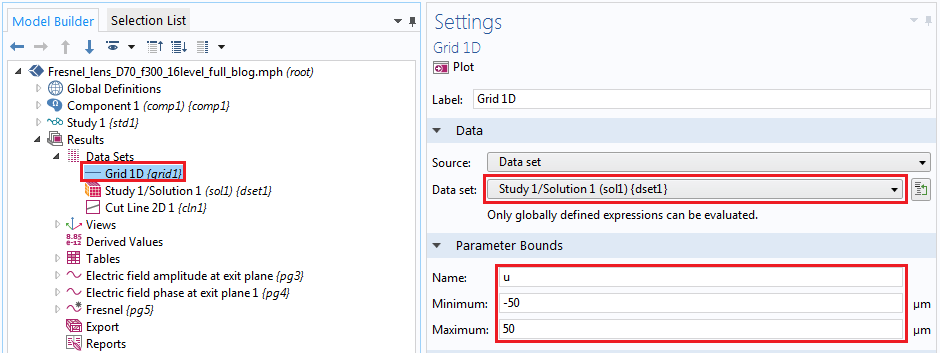
変換用のデータセットの設定.
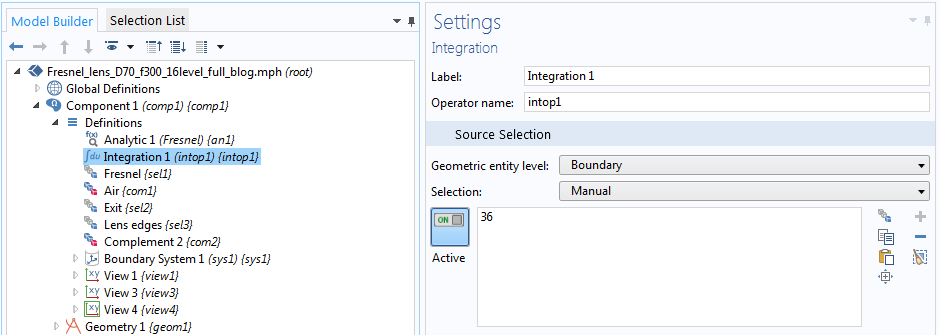
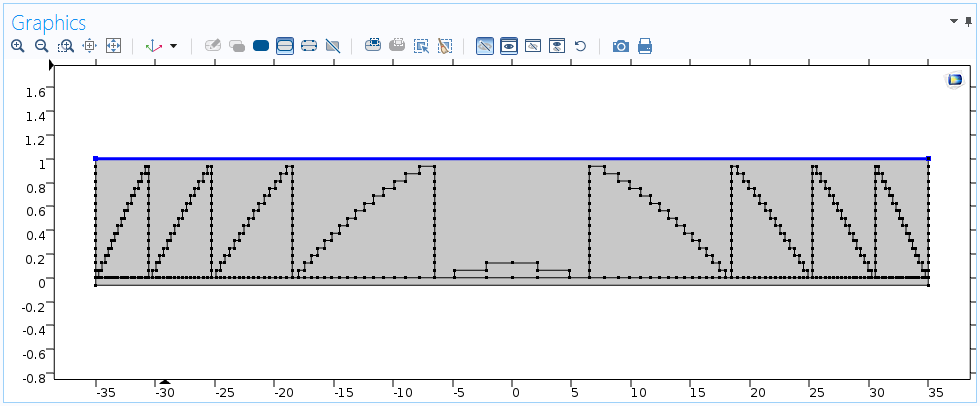
出口平面で定義されたintop1演算子(縦軸は縮尺どおりではありません).
最後に, 以下に示す1Dプロットでフーリエ変換を定義します. 前に変換用に作成したデータセットを指定し, dest演算子を使用して, uが行先の独立変数であることをCOMSOL Multiphysics に通知することが重要です.
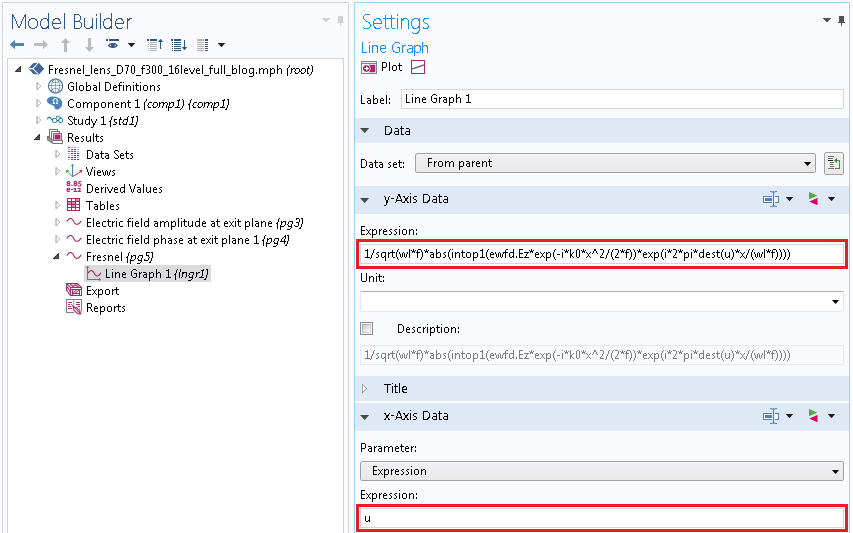
1Dプロットでのフーリエ変換の設定.
最終結果を次のプロットに示します. これは, 焦点面のマルチレベルフレネルレンズを通過する集束ビームの典型的な形です(参照2を参照). 中央に一次回折によるメインスポットがあり, ゼロ次(非回折)および高次回折によって引き起こされる弱い背景があります.
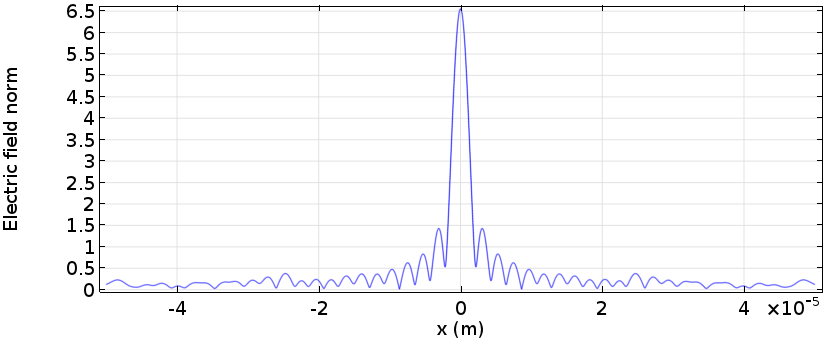
16レベルのフレネルレンズを通過する集束ビームの電場ノルムプロット.
おわりに
このブログでは, 計算された解にフーリエ変換を適用する実装方法を学びました. この機能は, COMSOL Multiphysicsでの長距離伝搬計算に役立ち, 電磁シミュレーションをフーリエ光学に拡張することが出来ます.
次のステップ
下のボタンをクリックして, フレネルレンズの例のモデルファイルをダウンロードします.
波動光学のシミュレーションについてもっと読む
- COMSOLMultiphysicsでのホログラフィックデータストレージのシミュレーション
- ホログラフィックページデータストレージシステムをシミュレートする方法
- COMSOLMultiphysicsでフーリエ変換を実装する方法
参考文献
- J.W. Goodman, Introduction to Fourier Optics, The McGraw-Hill Company, Inc.
- D. C. O’Shea, Diffractive Optics, SPIE Press.



コメント (0)