
今年7月, 私は第22回国際音響振動会議に参加する機会に恵まれました. イタリア人の同僚 Gabriele とともに COMSOL ベンダーブースを運営したほか, イベントのプレゼンターも務めました. 私のプレゼンテーションは, 熱粘性効果を含む音響放射力の測定方法に焦点を当てた, Henrik Bruus および Jonas Karlsen と共同執筆した論文に基づいています. 音響泳動効果についてさらに詳しく調べ, 私のプレゼンテーションで取り上げた研究結果を見てみましょう.
音響放射力とは?
音響放射力は, 音響場から小さな粒子への運動量の伝達によって発生し, その結果, 粒子に作用する正味の力になります. 音響流の関連現象では, 音響場によって正味の流体の流れが駆動され, 音響境界層で (流体への) 運動量の伝達が発生します.
どちらの現象も, たとえばマイクロ流体デバイス内で粒子や小さな生物 (細胞, タンパク質, 大きなウイルスなど) を移動, 制御, 分類するために使用されるため重要です. この種の粒子操作は, 音響泳動, つまり音による移動として知られています. 放射力は粒子に直接作用し, 音響流は粒子に抵抗を引き起こします. 効果の大きさや方向は, 粒子のサイズと機械的特性, および流体特性によって異なります. このような現象をしっかりと理解することは, 粒子を効率的に分類および操作するデバイスを製造および最適化するために不可欠です. 以前のブログ では, マイクロ流体デバイスで音響放射力と音響流をモデル化する方法を示しました.
第22回国際音響振動会議 (ICSV22) での私のプレゼンテーションは, いわゆる 2次摂動理論 を使用して音響放射力を詳細にモデル化する方法の拡張と一般化でした. 音響流力ブログシリーズ は, 放射力の理解に役立つ入門書であり, これらの力を計算するさまざまな方法も紹介します.
音響放射力を分析するためのさまざまなアプローチ
ここで, もう少し技術的になって, いくつかの方程式を取り上げてみましょう. ほとんどの物理問題の場合と同様に, さまざまな物理的仮定とさまざまな状況下で放射力の効果を記述および導出する方法はいくつかあります. ここでは, これらのさまざまなアプローチを簡単にまとめ, 説明します.
直接 FSI アプローチ
直接流体構造相互作用 (FSI) アプローチ では, 支配方程式の完全な (非線形) 系が動的問題として求解されます. 次に, 時間平均粒子運動を調べることで放射力を抽出します. 熱損失と粘性損失の両方を含めるには, ナビエ・ストークス方程式 をエネルギー方程式と一緒に解く必要があります. エネルギー方程式は, 本質的には 非等温流 です. 放射力に関連するすべての小規模な効果を捉えるために, 方程式を高い数値精度で解く必要があります.
2次摂動アプローチ
非線形支配方程式の完全な系の分析を簡素化するために, 問題を線形音響問題と線形時間平均2次問題に分割できます. これは, 2次摂動理論によって実現されます. たとえば, 圧力 p は p = p_0+p_1+p_2 と記述されます. 下付き文字 0 は背景特性 (平衡条件に応じて, 0 番目圧力はほぼ一定の単一気圧になる場合があります) を表し, 下付き文字 1 は古典的な音響場を表し, 下付き文字 2 は非線形効果を捉えるために必要な2次摂動場を表します. 異なる次数の方程式は順番に解かれます.
この理論では, 一般に, 物体に対する放射力 \Omega は次のように表されることが立証されています
(1)
ここで, \langle \cdot \rangle は時間平均を表し, \sigma_2 は応力に対する2次寄与, \mathbf{u}_1 は速度場における音響変化であり, 積分は粒子を囲む任意の閉じた表面上で行われます.
したがって, 放射力を求めるには, 音響問題 (1次摂動) と 2次摂動方程式の両方を解く必要があります. この方法は, ICSV22 で発表された研究で使用されました. これについては, 以下で詳しく説明します. 方程式は, 流体と固体の両方における熱損失と粘性損失を含めて解かれます.
損失なしの限界
流体は, 粘性境界層と熱境界層 (浸透深さ \delta_\textrm{tv}) よりもはるかに大きいサイズ a の粒子に対して損失がないものとして扱うことができます. つまり, \delta_\textrm{tv}/a \ll 1 です. この場合, 式2次応力は, (1) は, 遠方場では次のように簡略化できます
(2)
任意の物体の散乱場 p_1 と \mathbf{u}_1 を決定することで, 式 (1) の放射力を計算できます. 2次場を明示的に知る必要はありません. 参考資料セクションの 2 とブログ “音響放射力の計算方法” には, この例が2つ記載されています.
レイリー限界
レイリー限界では, 粒子は音響的に小さいと想定されます. つまり, k\cdot a \ll 1 です. ここで, a は粒子サイズ, k は波数です. 散乱理論を使用して, 粒子からの散乱場を導き出します. この限界では, 式 (1) で示される放射力は, 次のように減少します.
(3)
ここで, f_0 と f_1 は単極子と双極子の散乱係数であり, 下付き文字 \textrm{in} は, 小さな粒子の位置で評価された入射音場 (たとえば, 選別装置内の定在音場) を表します. 流体の圧縮率は \kappa_s で, 流体の密度は \rho_0 です.
このアプローチの全体的な仕組みは, 2つの散乱係数を見つけることです. いくつかの解析結果があります:
- 非粘性および断熱の場合, 結果は Gor’kov によって 文献 3 で示されています.
- 粘性を含む結果は, Settnes と Bruus によって 文献 4 で示されています.
- 文献 5 では, Karlsen と Bruus が完全な熱粘性理論を提示しています. ここでは, 小さな液滴からの散乱も求解され, 粒子内部の熱粘性効果も考慮されています.
- この分野の多くの結果は, いわゆる サスペンション音響学 で見つけることができます (文献 6 を参照).
COMSOL Multiphysics での方程式ベースのモデリング
最初のモデル系として, 超音波定在波内に置かれた小さな球状粒子に作用する音響放射力を決定することにしましょう. 前述のように, 式 (1) に示されているように, 詳細な摂動法を使用して放射力を求めることにしました. モデルには, 流体と固体の熱損失と粘性損失が含まれています.
最初のステップは, 音響場 (1次場) を決定することです. つまり, 流体の 熱音響 (周波数領域) フィジックスインターフェースと固体の 熱弾性 インターフェースを結合して方程式を解きます. 必要な結合は COMSOL Multiphysics で事前に定義されていませんが, ユーザーインターフェース (UI) で簡単に設定できます. その後, COMSOL Multiphysics は完全に結合された問題を解きます.
1次場が確立されると, 2次方程式の時間平均の方程式を解くことができます. したがって, ここからは 2次量の \langle \cdot \rangle 表記を省略し, 方程式に現れるときは常に, 時間平均の意味, \langle a_2 \rangle ¬\equiv a_2 で理解します.
これらの方程式の構造は, CFD モジュールの層流方程式と同じですが, ソース項が追加されています. 数値上の理由から, 定義済みの方程式を使用せず, 独自のバージョンを保守的な形式にキャストして実装することにしました. この手順は, 1次場から 2次解に伝わる数値ノイズを減らすために重要です. 非保守的な定式化では, 1次場の勾配を明示的に評価する必要があり, 数値ノイズが発生します. 質量, 運動量, エネルギー保存の方程式は次のとおりです:
(4)
\nabla\cdot[\rho_0 \mathbf{u}_2+\langle \rho_1 \mathbf{u}_1 \rangle] = 0 \\
\nabla\cdot [\mathbf{\sigma}_2 – \rho_0\langle\mathbf{u}_1\mathbf{u}_1^\textrm{T}\rangle \mathbf] = \mathbf{0} \\
\nabla\cdot [k \nabla T_2+\langle \mathbf{u}_1\cdot\mathbf{\sigma}_1\rangle + \alpha_0 T_0 \langle p_1 \mathbf{u}_1 \rangle – \rho_0 C_\textrm{p}\langle T_1 \mathbf{u}_1 \rangle] = 0
\end{aligned}
ここで, 2次場は時間平均値であると仮定します. 1次場は 2次方程式のソース項の役割を果たすことに注意してください.
方程式と境界条件の設定は, COMSOL Multiphysics で使用できる一般弱形式を使用してのみ可能でした. 新しい方程式を追加および定義する柔軟性は, この問題を求解するために最も重要でした.
結果
理論と方程式について説明しました. 次に, 見栄えの良いカラフルな結果を見てみましょう.
系の例として, 半径が a=1 \: \mu \textrm{m} から a=40 \: \mu \textrm{m} の小さな球状ポリスチレン粒子を見てみましょう. 粒子は空気に囲まれており, 2 MHz の定常超音波場内に配置されており, \delta_\textrm{v} = 1.6 \: \mu\textrm{m} および \delta_\textrm{t} = 1.9 \: \mu\textrm{m} となります. したがって, より小さな粒子の場合, 境界層の影響が大きく, ロスレス理論は不正確であると予想されます. さらに, 大きな粒子の場合, 選択した粒子サイズの範囲で, レイリー限界 k\cdot a \ll 1 の外側にあり, 0.04 < k\cdot a < 1.5 となります. これは, 解析理論の範囲外にあることを意味します.
振動する音圧場.
上のアニメーションは, 調和振動する音圧場 p_1 全体を表しています. 黒い円は, 式 (1) を評価するために使用されるさまざまな積分面を表していますが, 計算メッシュの制御にも使用されます. 粒子からの散乱場は下図のとおりです. この調和圧力振動は, 非線形効果により, 正味の時間平均放射力をもたらします.
粒子からの散乱場.
下の一連のアニメーションは, さまざまなシミュレーション分析の結果を示しています. 一番上の行の左側の図は, 粒子の周囲の温度変動 T_1 を表しています. 温度変化の程度は, 熱境界層または流体への浸透深さを示します. 右の図は, 小さなポリスチレン粒子の変形と固体内の一次温度変化を示しています. ここでも, 固体内部の熱浸透深さが捉えられています. 下の行に移動すると, 左の図は散乱音場の軸方向速度成分を表し, 右の図はこの場の半径方向速度成分を示しています.
さまざまなシミュレーションの結果. 左上: 温度変化. 右上: 粒子の変形. 左下: 散乱音響場の軸方向速度成分. 右下: 半径方向速度成分.
1次場を2次方程式に代入し (式 (4) を参照), 粒子の周りの局所的な定常流動を解きます. 圧力と速度の大きさは, それぞれ次の2つの図に示されています. 圧力 (単位: Pa) と速度 (単位: m/s) のスケールが非常に小さいこと (カラーバーで表示) に注意してください. たとえば, 入射駆動波に対する圧力は, 振幅 3\cdot 10^{-3} \: \textrm{Pa} です.
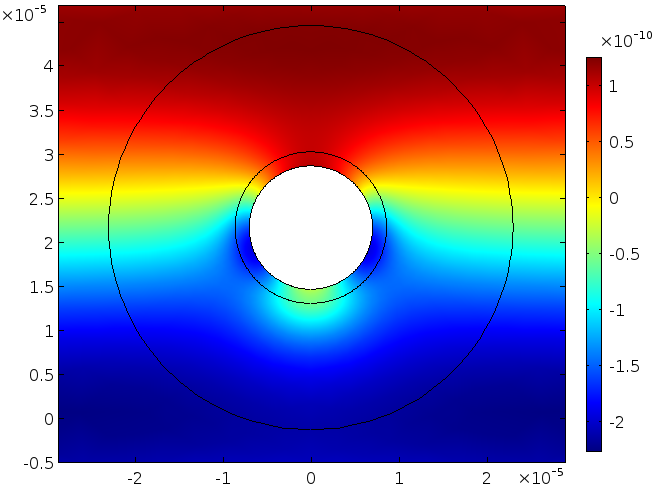
圧力場.
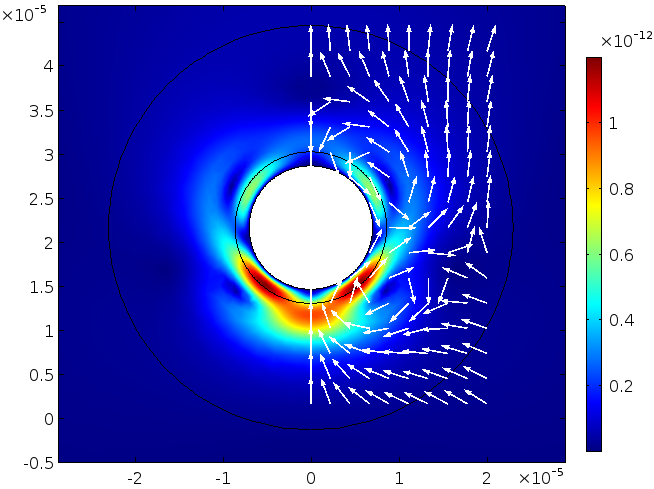
速度場.
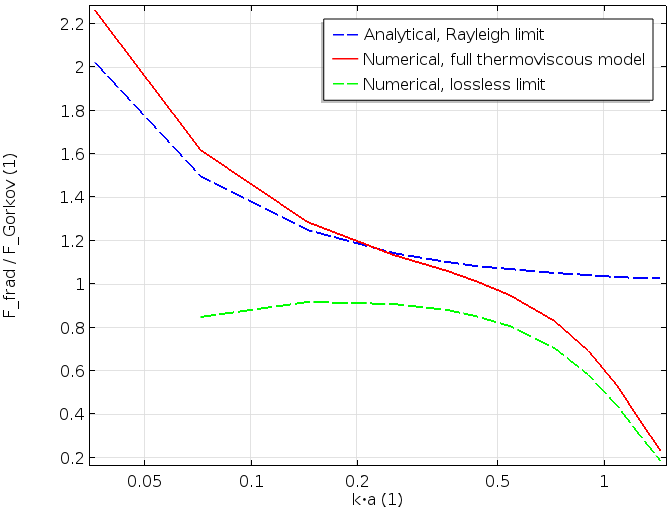
最後に, 1次および2次場がわかれば, (1) で示される力を導き出すことができます. 最初のグラフでは, 力が \delta_\textrm{v}/a (粘性浸透深さと粒子サイズ) の関数として表されています. 2番目のグラフでは, これは k\cdot a の関数として表されています. 放射力は, 無損失ケースとレイリー限界 (Gor’kov で表示) で評価された対応する力によって無次元化されます.
これらのグラフには3つの曲線が含まれています. 青い破線曲線は, レイリー限界で Karlsen と Bruus によって与えられた解析式です. 緑の破線曲線は, 式 (2) で与えられた無損失モデル (境界層を無視) で評価された力を示しています. 最後に, 赤い曲線は, 熱粘性損失を含む完全な数値モデルを表し, これは大きな粒子と小さな粒子の両方に有効です.
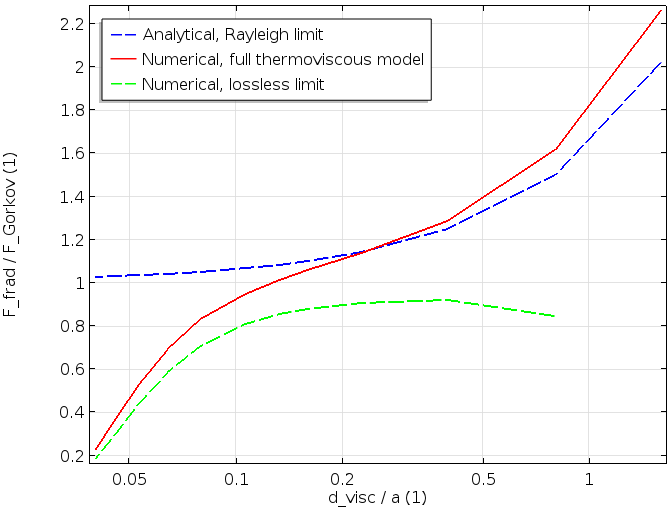
最初のグラフ (上図) は, 粘性損失と熱損失を含む完全なモデルが, 損失のない曲線 (\delta_\textrm{v}/a が小さい) を, 損失を含むが小さい粒子 (一定の材料パラメーターの場合は \delta_\textrm{v}/a が大きい) に結び付ける様子を示しています. 下図の2番目のグラフは, 同じ特性を示しています. 私たちが実装した詳細な熱粘性モデルは, 大きな粒子の限界 (緑の破線はロスレス) と小さな粒子の限界 (青の破線, レイリー限界の小さな k\cdot a) を結び付けます.
結論
ICSV22 に参加することで, デンマーク工科大学の Henrik Bruus 氏と彼の研究グループと共同で取り組んできた研究の一部を発表する機会を得ました. 実験と数値モデル化と並行して, 研究グループの研究により, 音響泳動現象の理論的な理解が深まりました.
私の発表は, 小さな球状粒子に作用する放射力の新しい数値的完全熱粘性解析に焦点を当てました (楕円体粒子は今後の研究で予定されています). このモデルは, 適用限界 (レイリー限界および/または無損失限界) において既存の結果とよく一致しています. この方法は非常に一般的なので, 任意の形状の粒子に簡単に拡張できます. このモデルは, 温度による粘度の変動など, より詳細な材料依存性を含めるようにさらに拡張することもできます.
その他の資料
-
- “Theory and Simulation of the Acoustic Radiation Force on a Single Microparticle in an Ultrasonic Standing Wave Including Thermoviscous Effects”, M. J. H. Jensen, J. T. Karlsen, and H. Bruus.
- “Efficient finite element modeling of radiation forces on elastic particles of arbitrary size and geometry”, P. Glynne-Jones, P. P. Mishra, R. J. Boltryk, and M. Hill.
- “On the forces acting on a small particle in an acoustical field in an ideal fluid”, L. P. Gor’kov.
- “Forces acting on a small particle in an acoustical field in a viscous fluid”, M. Settnes and H. Bruus.
- “Forces acting on a small particle in an acoustical field in a thermoviscous fluid”, (accepted) J. T. Karlsen and H. Bruus.
- Suspension Acoustics: An Introduction to the Physics of Suspensions, S. Temkin.






コメント (0)