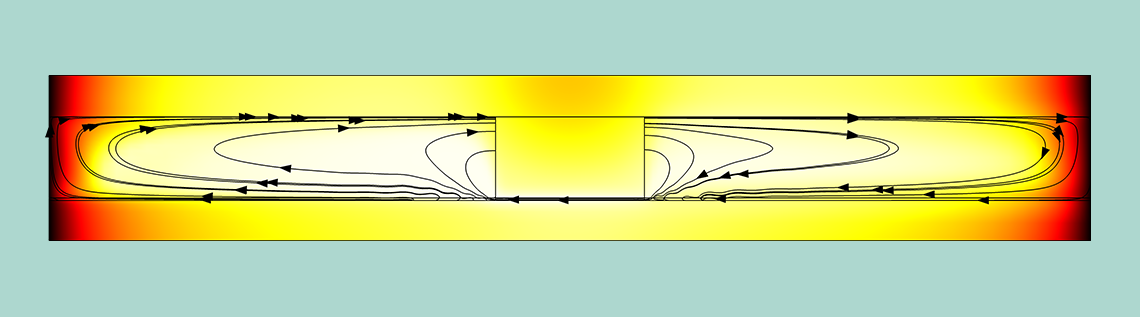
時間に依存するシミュレーションのログを追跡すると, ソルバーが使用する時間ステップや離散化次数が変化していることがわかります. シミュレーション中に, 時間ステップが小さくなり, 解答が完了するまでに時間がかかることがあります. ここでは, 時間ステップと離散化次数を選択するためのメカニズムについて説明します. 次回のブログでは, 時間ステップが小さい場合にシミュレーションの効率を上げるための対策についてご紹介します.
過渡シミュレーション
過渡シミュレーションでは, 時間変化を反映した離散的な解を計算する必要があります. 初期値から始まり, 未知の過渡的自由度は時間積分スキームによって決定されます. ある時間ステップで計算された解は, 与えられた許容範囲内で事前に定義された誤差範囲を満たす場合に受け入れられます. アダプティブ時間ステップアルゴリズムは, 大きすぎる時間ステップを使用する可能性があるため, すでに実行されたステップではエラーテストが通らないことがあります. このような場合には, 時間ステップを減らしてステップを繰り返します. また, 非線形ソルバーが最大反復回数内で代数方程式を解くことができない場合にも, 時間ステップが短縮されます. これらのメカニズムはいずれも余分な作業を伴うため, 時間依存シミュレーションが最適ではないほど長くなってしまいます.
このブログでは, 内部で使用されているメカニズムを理解し, ソルバーログで提供される情報を読み解くのに役立つことを目的としています. このブログの続きでは, これらのメカニズムを理解した上で, 小さな時間ステップが発生した場合に, 時間ステッピングをより効率的かつロバストに行う方法を例示します. まず, ソルバーログを見て, そこから何がわかるか見てみましょう.
時間依存型ソルバーログ
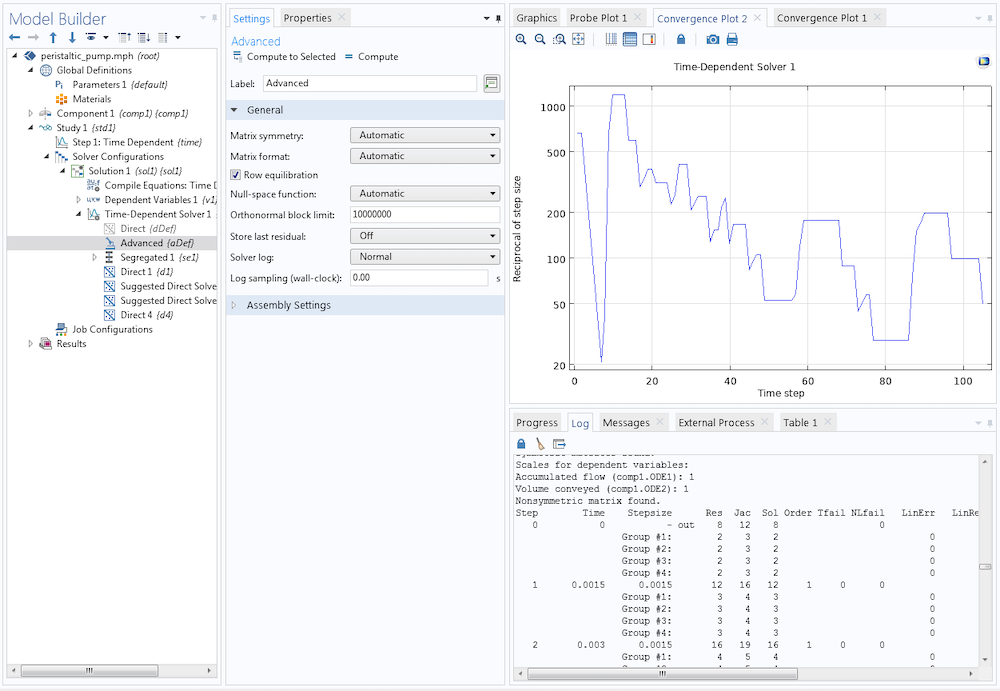
時間依存型ソルバーの典型的なソルバーログは次のようなものです.
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
1 |
2.6e-16 |
2.4e-16 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
ログには, 現在の時間Timeにおける時間積分ループの反復カウンターStepが表示されています. ここでStepsizeは現在の時間ステップのサイズです. 次の3つの列は, 残差アセンブリの総数(Res), ヤコビアンアセンブリの総数 (Jac), および線形代数系解の総数 ( Sol)の詳細を示しています.
このブログでは, 特に時間ステップ方式の離散化順序(Order), 適応的ステップサイズ選択の失敗数(Tfail), 代数(非線形)ソルバーの総失敗数(NLfail)に注目しています. これらの失敗の意味については, 以下のセクションで説明します. 各時間ステップの最後の線形問題の解に関する情報は, 線形代数系エラー推定値(LinErr)および線形代数系残差のサイズ( LinRes)で得られます.
ソルバーログに記載されているすべての時間ステップが見つからない場合は, 時間依存ソルバーの詳細ノードの一般セクションで, ログサンプリング(ウォールクロック)を0に設定することができます. ソルバーログを詳細に設定することで, 個々の代数ソルバーの反復からのプリントアウトをソルバーログに追加すると便利な場合があります. シミュレーションの過程での時間ステップの変化は, 対応する収束プロットで見ることができ, すべての時間ステップでステップサイズの逆数が出力されます. このプロットの値が大きいほど, 時間ステップが小さいことを示しています.
ソルバーが非常に小さな時間ステップをとっている場合, いくつかの異なる原因が考えられます. 一つは, モデルがある種の特異点(物理的なものかどうかに関わらず)に近づいていること, あるいは解が無限に飛び出していることが考えられます. もう一つの理由は, モデルが滑らかな時間変化を与えない(例えば, メッシュが粗すぎるため)ため, どの時間ステップでも誤差推定値を満たすのが難しいということです. 3つ目の理由は, 非線形性の取り扱いが難しい(代数的なソルバーが収束しない)ことです. 時間ステップの変化が何を意味するのかを詳しく知るためには, 時間ステップの決定をより深く掘り下げる必要があります. ここでは, COMSOL®ソフトウェアで使用されているいくつかの時間ステップスキームを見てみましょう.
離散型時間ステッピング方式
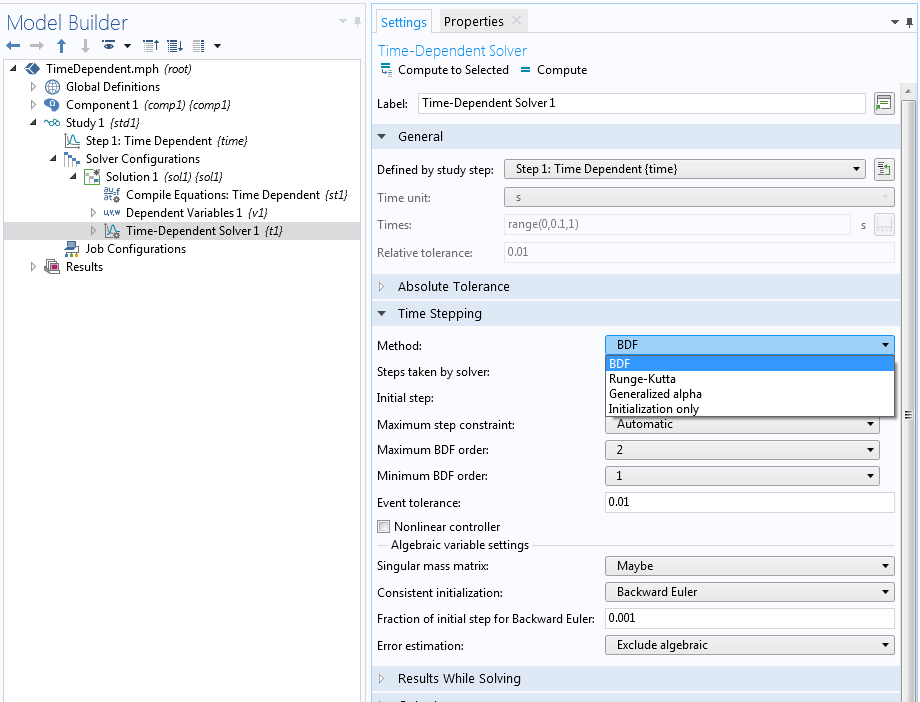
COMSOL Multiphysics® ソフトウェアの時間依存ソルバーには, 3 種類の時間ステップ法があります. 陰的後退微分法(BDF), 一般化アルファ法, 陽的なルンゲ・クッタ法の 3 種類です.
BDFソルバーは, 可変の離散化次数とステップサイズの自動選択を備えた後退微分式を使用する陰的ソルバーです. 高次のスキームは, 解の品質が許す限り使用され, 低次のスキームは, さらなるロバスト性が必要な場合に使用されます. BDF法はその安定性で知られており, デフォルトでは拡散, 対流, 反応を含む問題に使用されています.
一般化アルファ法は, 2次の陰解法で, 構造力学の問題でよく使われますが, 波動伝播の問題にも適しています. 一般化アルファ法は, 高周波数の減衰を制御することができ, 一般的に2次のBDF法よりも減衰が少なくなります. 多くの場合, BDFよりも精度が高いですが, 安定性も劣ります.
一般化アルファ法は, 構造力学の問題でよく使われる2次の陰解法ですが, 波動伝播の問題にも適しています. 一般化アルファスキームでは, 高周波の減衰をコントロールすることができ, 通常, 2次のBDFスキームよりも減衰が少なくなります. 多くの場合, BDFよりも精度が高いですが, 安定性も劣ります.
ルンゲ・クッタ法は, 常微分方程式(ODE)の系によく用いられる陽解法です. 有限要素法 (FEM)で解く問題では, 通常, あまり効率的ではありません.
このブログでは, BDF時間ステッピング法に焦点を当てます. BDFスキームは, 時間依存ソルバーの時間ステッピングセクションで選択できます. モデルの物理的性質によっては,すでに選択されている場合もあります.
時間ステップ選択の設定
時間依存のスタディステップでは, 開始時間から終了時間までの時間と中間ステップの明示的なリストを指定することで, 時間リストを提供します. 範囲演算子を使用すると, 中間時点のリストを素早く指定できます. よくある誤解ですが, これらの中間点は, ソルバーが行う指定の時間ステップではなく, ポスト処理や評価のために解が保存される出力時間です. ソルバーが取る時間ステップは, デフォルトでは,各時間ステップの誤差を望ましい範囲内に収めるようなアルゴリズムによって決定されます. 以下の設定は, 時間依存ソルバーの時間ステップセクションのソルバーによるステップで, 時間ステップの実際の選択に影響を与えるために利用できます.
- フリー:局所的な誤差推定値に基づいて, 適応的な時間ステップサイズが選択されます. 時間ステップは, 現在の誤差推定値と許容値との関係に基づいて縮小または拡大されます. 実行されたステップがまだ誤差推定値を満たしていない場合, ステップは縮小されたステップでやり直されます(
Tfailはソルバーログに記録されます). このようなステップサイズの縮小は, 失敗したステップが無駄になるため, コストがかかります. また, 非線形ソルバーループが最大反復回数以内に収束しない場合にも, 時間ステップが短縮されます(NLfailがソルバーログに記録されます). 指定された出力時間は, ソルバーが行う時間ステップとは関係ありません. 指定された出力時間での解は, ソルバーが実行したステップ間の補間によって計算されます. - 厳密:フリーの設定と同じですが, ソルバーは指定された出力時間にも解けるように時間ステップを調整します.
- 中間:自由設定と同じですが, ソルバーは出力時間で定義された各サブインターバル内の少なくとも1つの時間についても解くように時間ステップを調整します.
- 手動:自動ではなく, ユーザーが指定した時間ステップを実行します. 時間ステップは, 定数, グローバル変数の式, または単調な時間値のリストの間の時間間隔から決定されます.したがって, この時間ステップは完全にユーザーが制御でき, 時間ステップの誤差テストは無効になります. ただし, 代数ソルバーの誤差推定値はまだ有効であり, したがって許容範囲を考慮することが重要であることに注意してください. 最大反復回数の後に代数的な誤差推定値が満たされない場合, 時間ステップは減少します.
以下のセクションでは, フリー設定での時間ステッピングに焦点を当てます. 中間 および厳密 な時間ステップは, 適応的な時間ステップ選択の利点と, 特定の重要なモデリング時間またはモデリング時間ステップを手動で実施することを組み合わせるために使用できます. 厳密な時間ステッピングでは, ユーザーが指定した時間リストの補間を避けることができますが, これはアプリケーションによっては重要なことです. ただし, ステップごとに出力を補間することを避けるには, フリー設定において保存時間:ソルバーによる選択に設定します.
時間離散化
COMSOL Multiphysics® では, 時間依存偏微分方程式(PDE)の系を, 有限要素法による空間離散化によって ODE(または微分代数方程式,すなわち DAE)の陰的な系に変換します(不連続ガラーキン法ではありません). 時間離散化(最も単純なケースでは, 後退オイラー法)を用いて, 未知の自由度に対する代数方程式のセットを生成します. 各時間ステップにおいて, 代数方程式は, 自動線形化を用いたニュートン法(通常,完全連成ソルバーまたは減衰ニュートンソルバー付き分離ソルバー)によって解かれます.得られた線形方程式は,直接ソルバー(MUMPSやPARDISOなど)または反復ソルバーによって解かれます.
COMSOL Multiphysics® の有限要素離散化から得られる陰解法 ODE 系は, ユーザーが提供した相対的および絶対的な許容範囲のもとで, 事前に定義された精度要件で解かれます. この要求には, 時間ステップ(ソルバー)の誤差と代数方程式(ソルバー)の誤差の2 種類があります.1つ目のタイプは, フリー, 中間, 厳密の各方法ではアクティブですが, 手動法ではアクティブではありません. 2番目の要件は常にアクティブです.
手動法を使用しているときには許容範囲が使用されないと考えるのはよくある誤解です. 時間ステップ誤差の要件は, 使用する手法の局所的な切り捨て誤差の推定値に基づいています. 代数ソルバーの誤差は, 定常問題を解くときとよく似た要件,すなわち解ベクトルの増分の大きさに基づいています. しかし,この誤差推定値の正規化は, 時間依存ソルバーが使用する正規化に合わせています. これは, 代数誤差のノルムを時間ステップ誤差のノルムと同等にするためで, 代数ソルバー誤差のスカラー因子(許容因子)を減らすことで, 時間ステップ誤差と比較して代数誤差を均等に抑制することができます. 計算された解が代数的な誤差で汚染されるのを避けるために, この係数を減らすことが重要な場合があります. 実際, 代数誤差が時間ステップ誤差よりも小さくなければ, 時間ステップの不安定さや誤差テストの失敗など, 別の問題が発生する可能性があります.
後述する2つの要件は, ODE系を解く上で中心となるものです. しかし, この系がFEMの離散化に起因する場合, 他の誤差の原因が考慮されていないことを念頭に置くことが重要です. 例えば, FEM法の切り捨て誤差, 有限要素積分の近似に数値手法を用いた場合の求積誤差, 実際の幾何学的形状を多項式で表現した場合の幾何学的近似誤差などがあります.
局所的・大域的な切り捨て誤差と離散化誤差
ここで, 切り捨て誤差について詳しく見てみましょう. 有限要素法による離散化から, 次のような形式の暗黙のODEが得られます.
L(\dot{U},U,t) = 0, \ \ U(0) = U^0
ここで U=[U_1(t), …, U_N(t)] は, 未知数のベクトルまたは時間依存の自由度であり, L 残差ベクトルと呼ばれます.
ここでは, 1次の時間微分のみが含まれていると仮定し, 簡単のために制約処理を無視しています. q可変ステップサイズのBDF法は, \tau_k次の関係を用いて定義されます.
U^k \approx \sum_{i=1}^q \alpha_{k,i} U^{k-i} + \tau_k \beta_k \dot{U}(t_k)
ここで, U^kという表記は, 解U(t_k)をステップ依存の係数\alpha_{k,i}と\beta_kで近似したものとして使われています.
この表現は, 名前の後退微分式を示しています. この式は, 時間微分をなくして代数問題を得るために使用することができます.
L\left(\frac{U^k-\sum_{i=1}^q \alpha_{k,i} U^{k-i}}{\tau_k \beta_k},U^k,t_k\right) = 0.
時刻t_kでの局所的な打ち切り誤差はe_{k} := U^k – U(t_k;U^{k-1})と定義され, U(t_k;U^{k-1})はU(t_{k-1}) = U^{k-1} を満たす正確な解です. この解をテイラー展開すると, 次のようになります.
L(\dot{U}(t_k;U^{k-1})+O(e_k/\tau_k) + O(\tau_{k}^q), U(t_k;U^{k-1})+e_k,t_k)=0,
また, 残差をテイラー展開すると, 次のようになります.
L(\dot{U}(t_k;U^{k-1}), U(t_k;U^{k-1}),t_k)+\frac{\partial L}{\partial \dot{U}}(O(e_k/\tau_k) + O(\tau_{k}^q)) + \frac{\partial L}{\partial U}e_k + {\rm h. o. t.}= 0,
ここで, 第一項は定義により同値的にゼロである. 質量行列D = -\frac{\partial{L}}{\partial \dot{U}}の逆が存在するという条件のもと, オーダーqのスキームに対して次のようになります.
|e_k| = O( \tau_k^{q+1} )
質量行列の逆が存在しない場合はDAEとなり, 誤差解析はより複雑になりますが, 適応的な時間ステップの原理は同じです. ここでは, 時間ステップがステップごとに任意に大きく変化しないように, 異なる時間ステップがお互いにある程度関連していることも仮定しています.
重要なのは, グローバルな切り捨て誤差E^k := U^k-U(t_k)です. この誤差は,すべての局所的な誤差からの寄与です. 概念的には, すべての局所的な誤差は加算されます. 次数qの過渡的なスキームで, 一定の時間ステップ\tau_k = \tauの場合,(適切な正規化をして)適切な仮定の下で次のように求められます.
|E^{k}| \le C \tau^q
ここで, 定数Cは問題に強く依存します. 実際のODE問題の局所的な誤差は, 方程式の性質によって増幅されたり減衰されたりするので, 局所的な誤差の単純な総和という概念は大目に見ておく必要があります. 例えば, 誤差が増幅される場合には, 定数が非常に大きくなります. さらに, 一 定の時間ステップで得られた局所誤差は, シミュレーション中に大きく変化する可能性があります. これらの観察結果から, 時間ステップを選択する際の良い戦略は, 時間ステップ中に局所誤差を同じレベルに保つことであると考えられます. また, 局所的な誤差のレベルを調整することで, 大域的な誤差を制御し, 必要に応じて低減することも可能であると考えられます.
与えられた離散化スキームでは, 誤差推定値の陽的表現は, 次のように与えられます.
e_{k} = C_k \tau^{q+1} U^{(q+1)}(t_k) + O(\tau^{q+2})
ここで,C_kと過去のqステップサイズ\tau_j,\, j\le kの計算可能な関数です.
例えば,BDFの陽的な類似性を利用して,次のような予測値を計算することができます.
U^{k(0)} = \sum_{i=1}^q \alpha_{k,i}^{\rm pred} U^{k-i} + \tau_k \beta_k^{\rm pred} \dot{U}(t_{k-1}).
漸近法による解析では
U^k – U^{k(0)} = \bar{C}_k \tau ^{q+1} U^{(q+1)}(t_k) + O(\tau^{q+2})
を計算可能な定数\bar{C}_kで表したものです.
|e_{k}| \approx |\bar{e}_k| := \frac{C_k}{\bar{C}_k} |U^k-U^{k(0)}|.
この計算可能な式は,COMSOL Multiphysics® では局所的な切断誤差の近似値として使用され, その近似値は時間ステップの制御または適応に使用されます.
BDF時間ステッピング方式の時間ステップ制御
BDF時間ステップ方式の時間ステップは,絶対公差Aと相対公差Rに対して|\bar{e}_{k}| \le A + R |U^{k}|の場合に受けいれられます.M場jの自由度がN_jの場合, 誤差推定値の加重平均平方根ノルムがRの場合に時間ステップが受けいれられます.
\|\bar{e}_{k}\|^2_{\rm WRMS} := \frac{1}{M} \sum_j \frac{1}{N_j} \sum_i \frac{ |\bar{e}_{k,i}(q)|^2}{(A_i + R |U^{k}_i|)^2} < 1
は1よりも小さくなります. ここで \bar{e}_{k,i}は, 時刻U_i^kにおけるスケール化されたまたはスケール化されていない場の成分t_kの局所的な打ち切り誤差の推定値であり, スケールされたまたはスケールされていない絶対的な許容値A_iである. スケール化されたバージョンおよびスケール化されていないバージョンの詳細については, COMSOL Multiphysics Reference Manualの陰的時間依存ソルバーアルゴリズムの項を参照してください.
時間ステップごとの誤差は 2 つの要素に依存することがわかります.
- 時間ステップの大きさ, \tau_k
- 離散化スキームの次数q
高次のスキームは, より多くの作業を必要とするため, より高いコストでより高い精度が得られます. また,時間ステップが短いと, 合計でより多くの時間ステップを計算する必要があるため,高いコストでより高い精度が得られます.適応型BDF時間ステップ法は,次数と時間ステップサイズの両方を適応させることで,必要な精度を維持しながらコストを最小化しようとするものである. この方式では, 時間ステップと次数について高度な推測を行いますが, それでも現在の時間ステップの結果が誤差限界に従わないことがあります. この場合, 時間ステップはより小さな時間ステップで繰り返され\tau_k’, ステップの失敗Tfailが記録されます.
代数的な誤差の影響を抑制する
非線形問題では, 時間ステップごとに非線形方程式系を解く必要があることに注意してください. これは通常, ニュートン法のような反復法で行われますが, これには追加の代数的誤差が伴います. さらに, ニュートン法における線形化された方程式は, 線形化された系の正確な解をある程度までしか近似しない反復線形ソルバーで解かれるかもしれません.
非線形ソルバーは, あらかじめ定義された反復回数で収束しないことがあります. このような場合, 必要に応じてヤコビアン行列を更新し, 時間ステップを減らします. ログを見ると, NLfailカウンターが増加していることがわかります. 代数ソルバーの誤差は, 時間ステップkにおける m回目の反復の増分U^{k,m}をチェックすることで推定されます. ここで, U^kは, ニュートン反復mの近似値です(例えば, SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solversを参照してください. )
代数的誤差|U^k-U^{k,m}|は, 切断誤差を汚染し, 安定性に影響を与える可能性があります. 代数誤差が十分に小さいことを確認する必要があります. 許容誤差(完全連成ソルバーおよび分離ソルバーの方法および中止セクションで設定)は, 切断誤差に比べて代数誤差を抑制するために使用できる安全係数です. 切断誤差に使用される加重ノルムは, 同様の形式で代数誤差にも使用されます. 許容誤差を小さくすると, 一般的に非線形ソルバーの反復回数が増える(または同じになる).
個々の時間ステップでは, 許容差係数を小さくして方程式を解く方がコストがかかります. ただし, 大きすぎる許容差を使用すると代数的な誤差が生じ, 時間ステップ法が乱れて, 時間ステップの選択が正しくない, 不正確な方法,または不安定な方法になることがあるので注意が必要です. 最後の2つの効果は, 手動による時間ステップ法でも発生します.
時間ステップ選択と次数選択
次に, BDFスキームの時間ステップ選択法について説明します.時間依存ソルバーでは, 絶対公差と相対公差で各積分ステップの誤差を制御します. 相対的な許容値Rは, 通常, フィジックスの設定によって決定されますが, 時間依存型のスタディステップでは, 手動制御に切り替えることができます. デフォルト値はR=0.01です. 絶対的な許容差Aは, 時間依存ソルバーの絶対的な許容差のセクションで設定できます. 公差法の因子オプションでは, 絶対公差は相対公差に指定した因子を掛けたものになります. マニュアルオプションでは, デフォルトがA=0.001の場合, 詳細な値を指定することができます. 絶対公差は, 変数リストを使って各場に個別に適用することができます.
具体的には, BDFは, k番目の時間ステップにおける局所的な切り捨て誤差の推定値を計算し, その誤差の推定値が不等式\|\bar{e}_{k}\|_{\rm WRMS} < 1を満たすことを要求します. 時間ステップのメカニズムでは, 特別に扱われる初期段階があります. 最初の数ステップは, ステップサイズ\tau_kを2倍にして次数を上げ, 局所的な誤差のテスト\|\bar{e}_{k}\|_{\rm WRMS} < 1が失敗するか, 解の滑らかさをチェックするメカニズムによって次数qが減少するか, または次数qが最大次数q=5に達するまで, 各ステップの値q=1,2,3, …を取ります. BDFスキームでの次数の選択は, スケール化された微分ノルム |\tau^k U^{(k)}| が , q付近で単調kに減少するという要件に基づいています. これらのノルムは, 次の事実を用いて再び推定されます.
\tau^{q+1} U^{(q+1)} \approx T(q) := (q+1) \bar{e}_k.
ステップと次数の選択は, T(q)の単調性のテストから始まります. T(q)の値が減少するということは, 解が滑らかであり, 順序を増やすことができることを示しています. もしT(q) が qとともに増加するならば, 順序は減少します. それ以外の場合は, 次数qを維持します. 次に, 局所誤差テストを行い, 失敗した場合は, 次数q’=q, 新しいステップサイズ\tau’でステップをやり直します. 後者は, O(\tau^{q+1})の漸近挙動に基づいています. また, \bar{e}_kでは, 補正された時間ステップ\bar{e}_{k,\tau} > A + R |U|において, 少なくとも\tau’, at least \bar{e}_{k,\tau’} = A+R|U|が成立することを要求しており, これにより, 新たな時間ステップ\tau’が発生します.
\frac{A+R|U|}{\bar{e}_{k,\tau}}= \frac{\bar{e}_{k,\tau’}}{\bar{e}_{k,\tau}} = \left( \frac{\tau’}{\tau} \right)^{q+1} < 1
を通して
\tau’ =\left(\frac{A+R|U|}{\bar{e}_{k,\tau}}\right) ^{1/(q+1)} \tau
を導きます. ここでは, 追加の安全係数が導入されています.
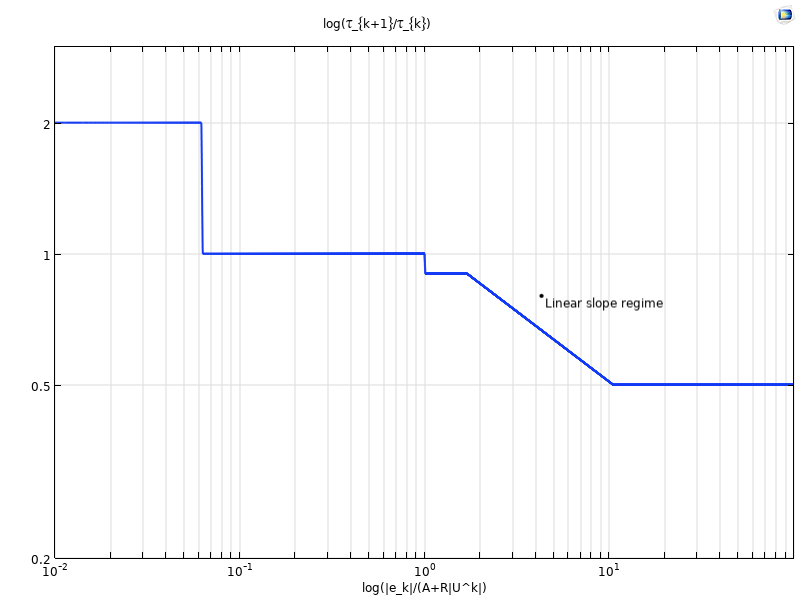
誤差が許容値よりも小さい場合, いわゆるデッドビートと呼ばれる領域が存在し, 誤差が許容値の16倍になるまで時間ステップを増やさないようにします. その後, 時間ステップを2倍にします. なお, 時間ステップの決定は, ほとんどがリミッターによって規制されています. レギュレーターは, 直線的な傾きの領域でのみ, 与えられた公式に基づいています. この体制は, 推定された局所誤差が本来あるべきものよりも大きく, 時間ステップを減少させる必要がある場合に支配されます. 以下の図(Ref.1の対応図との対比)では, 直線的な傾きの領域-1/(q+1)を特定することができます. ここで, \log(\tau_{k+1}/\tau_{k})は, \log(|\bar{e}_k|/(A+R|U^k|)) に対して出力されます.
局所誤差テストが合格した場合, そのステップと次のステップの次数が調整されます. 前のステップで次数が変更されていた場合, 次では変更はありません. 最後のq+1ステップが一定の次数q<5と一定のステップサイズで行われていた場合, BDFは次数の増加または減少を検討します. 次数qは, T(q)がqより減少していれば増加し, T(q)がqより増加していれば減少します. 詳細は, IDA solver in the Suite of Nonlinear and Differential/Algebraic Equation Solvers (SUNDIALS)のIDAソルバーのドキュメントに記載されています.
自動時間ステップおよび次数選択のまとめ
このブログでは, BDF時間ステッピングスキームのステップサイズと次数の自動選択メカニズムについて説明しました. これらのメカニズムは, 低コストかつ最大のロバスト性で, 規定の許容範囲に従った解の精度を保証するように設計されています. 実際には, このメカニズムを使用すると, 時間ステップが非常に小さくなり, シミュレーション時間が長くなることがわかりました. 時間ステップが小さすぎたり, 時間依存や非線形ソルバーのステップが何度も失敗する場合は, モデルの構成やソルバーの設定をさらに調整する必要があります. また, 基礎となるモデルが適切な解を持っているかどうかを常に確認する必要があります.
次回のブログでは, 例を挙げて, 時間ステップが小さすぎる場合にどのようなソルバーの設定を調整すればよいかをご紹介します. ご期待ください.
参考文献
時間依存モデルの解法の詳細については, COMSOL ナレッジベースをご覧ください.
参考文献
- G. Söderlind, L. Wang, “Adaptive time-stepping and computational stability“, J. Comp. and Appl. Math., vol. 185, pp. 225–243, 2006.


コメント (0)