弱形式の簡単な紹介

これは, 日常生活で有限要素解析やベクトル計算を使って育っていないけれども, 物理的な直感と基本的な計算の助けを借りて弱形式について学ぶことに興味がある人のための弱形式の紹介です.

弱形式について簡単に

COMSOL Multiphysics でシミュレートされるさまざまな種類の物理の多くでは, 数学モデルを構築するために舞台裏で弱定式化, つまり弱形式が使用されます. 弱形式を理解することで, COMSOL ソフトウェアの内部動作を理解するのに役立つだけでなく, モデルに含まれる特定の物理に対して利用できる組み込みインターフェースがない場合に独自の方程式を記述できるようになります.

同僚の Bettina Schieche のブログ “弱形式の強さ” もぜひお読みください.

簡単な例

熱源のない定常状態での 1D 熱伝達の具体的な例を考えてみましょう. 具体的には, $1\le x\le 5$ 区間で定義されるドメイン内の位置 x の関数としての温度 T に注目します. 簡単にするために, 熱伝導率は 1 であると仮定します. すると, 正の x 方向の熱流束 q は, 温度 T の勾配によって与えられます:

(1)

そして, 熱流束の保存 (領域内に熱源がない場合) は, 単に次のように表されます

(2)

これは, 私たちが解きたい主な方程式です. その解は, 領域内の温度プロファイルを与えます. この形式の方程式は, さまざまな分野で使用されます. たとえば, 静電気学では, T は電位に置き換えられ, q は電場に置き換えられますが, 弾性学では, T は変位になり, q は応力になります

ここで, COMSOL Multiphysics が結合されたマルチフィジックス問題を簡単に求解できる理由がわかります. どのような物理的メカニズムが関係していても, それらは方程式でモデル化され, 方程式が書き出されると, COMSOL ソフトウェアのコアアルゴリズムによって離散化されて簡単に求解できます.

一部の読者は, 解析解が非常に簡単な数学または物理的な議論で簡単に得られるのに, なぜこの一見単純すぎる例を選んだのかと疑問に思うかもしれません. その理由は2つあります:

1. ここでは, 弱形式の中心となる考え方に焦点を当て, 複雑な物理系の数学に惑わされないようにしたいと思います.
2. 以降では, 例を複数の領域に拡張して, 境界条件を介して2つの方程式系間の結合を示します. 今, より複雑な例から始めると, 後で例を拡張したときに中心となるテーマがほぼ確実に不明瞭になります.

弱定式化

方程式 (2) には, 熱流束の1次導関数 q, または温度の2次導関数 T が含まれており, 温度プロファイルの微分可能性が制限される可能性がある実際の状況では, 数値的な問題が発生する可能性があります. たとえば, 隣接する材料の熱伝導率が異なる境界では, 温度 T の1次導関数は不連続になり, T の2次導関数は数値的に評価できません. 弱形式の主なアイデアは, 微分方程式を積分方程式に変換して, 導関数を評価する際の数値アルゴリズムの負担を軽減することです.

微分方程式 (2) を積分方程式に変換するには, 単純な最初のアプローチとして, ドメイン全体にわたって積分することが考えられます $1\le x\le 5$:

これは, 領域全体の $\partial_x q(x)$ の 平均値 がゼロになることを求めています. 確かに, これは, 区間 $1\le x\le 5$ 内のどこでも $\partial_x q(x)$ がゼロになることを求めている元の微分方程式と比較すると “弱すぎる” ように見えます. これを改善するために, 代わりに, 非常に狭い領域での $\partial_x q(x)$ の平均値がゼロになるように求めることができます. たとえば,

積分には, x=3.5 付近の $\partial_x q(x)$ の値のみが含まれます. したがって, 上記の関係では, ゼロからあまり離れていないことが必要です: $\partial_x q(3.5) \approx 0$. 同じ考え方を領域全体のすべての位置 $1\le x\le 5$ に拡張すると, 元の微分方程式は次のような積分方程式の集合で近似できることがわかります:

(3)

積分方程式の数が多いほど, 近似は良くなります. そのような積分方程式の数が無限である限り, 元の微分方程式を復元します. すべての積分方程式を書き出すのは面倒で不可能ですが, 同じアイデアを別の方法で適用できます.

主なアイデアは, 狭い範囲で $\partial_x q(x)$ の値をサンプリングすることです. これは, 上記の式 (3) で狭い範囲で積分することによって行われます. 同じ種類のサンプリングは, 以下の図に示すように, 狭い範囲でのみ自明でない重み関数 \tilde{T}(x) を被積分関数に掛けることによって実行できます:

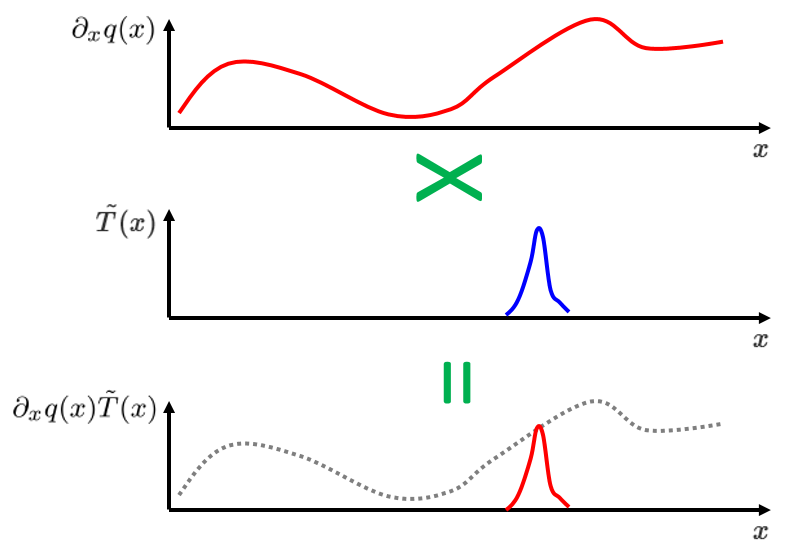
次に, さまざまな重み関数 \tilde{T}(x) について, 積 $\partial_x q(x)\tilde{T}(x)$ をドメイン全体 $1\le x\le 5$ にわたって積分できます. 各重み関数は, 異なる x 値を中心とした狭い範囲に積分関数の寄与を制限し, 式 (3) の積分方程式の集合と同じ効果を実現します. これにより, 関係式が次のように表される弱定式化が導かれます

(4)

は, 一般に テスト関数 と呼ばれる一連の重み関数 \tilde{T}(x) に対して成立するはずです. x のすべての値, たとえば x=3.5 に対して, x=3.5 を中心とした狭い重み関数であるテスト関数 \tilde{T}(x) を選択できます. このテスト関数を式に代入すると, (4) は, x=3.5 付近で $\partial_x q(x)$ の値をサンプリングするため, ゼロからあまり離れていないことが必要です: $\partial_x q(3.5) \approx 0$.

多数の狭い重み関数をテスト関数として式 (4) に代入すると, それぞれが区間 $1\le x\le 5$ 内の異なる位置を中心とするため, 関数 $\partial_x q(x)$ の値はドメイン内のどこでもゼロにクランプされます.

脚注: 上の図では, まだ解が見つかっていないことを強調するために, 意図的に $\partial_x q(x)$ を方程式の最終解ではなく任意の曲線としてプロットしました. 後の求解プロセスでは, この任意の曲線は一連のテスト関数によって上下に押し上げられ, 最終解の形状に到達します.

微分階数の削減

式 (4) の積分関数の微分階数は, 式と同じであることに注意してください. (2) (結局, 同じ関数 $\partial_x q(x)$ です) が, 部分積分法を使用して簡約できます:

(5)

これで, 方程式には熱流 q の導関数がなくなり, 温度 T に関して, 微分階数が 2 から 1 に減ります. では, 先ほど方程式に登場したテスト関数 \tilde{T}(x) の1次導関数はどうでしょうか?

前のセクションで見たように, テスト関数は方程式の解を見つけるためのツールとして機能します. したがって, テスト関数には, 都合よく微分可能な形式を自由に選択できます.

自然境界条件

式 (5) の最初の2つの項は, ドメイン境界 x=1 と x=5 における熱流束とテスト関数を含み, 熱流束 q は正の x 方向に定義されます. これをドメインから出ていく流束で書き直し, 右側に移動することができます:

(6)

ここで, $\Lambda$ は出ていく流束で, 添え字 1 と 2 はそれぞれドメイン境界 x=1 と x=5 を表します \Lambda_1\equiv -q(x=1) \mbox{, } \Lambda_2\equiv +q(x=5) \mbox{, } \tilde{T}_1\equiv \tilde{T}(x=1) \mbox{, } \tilde{T}_2\equiv \tilde{T}(x=5).

また, 熱流束関係 (1) を使用して, 温度 T とそのテスト関数 \tilde{T} に関して積分関数を記述しました. 式の右側は, 熱流束に関して境界条件を割り当てる自然な方法を提供します. 最も簡単な方法は, \Lambda_1 と \Lambda_2 の両方をゼロに設定して, 断熱境界条件 (境界を通過する熱流束なし) を取得することです.

COMSOL Multiphysics で熱伝達のデフォルトの境界条件が “断熱” で, 固体力学のデフォルトの境界条件が “自由 (境界力なし)” であるのは, まさにこのためです. 流束または力 (解く変数の1次導関数) を指定するこの種の境界条件は, 一般に 自然境界条件 または ノイマン境界条件 と呼ばれます.

固定境界条件

一般に 固定境界条件 または ディリクレ境界条件 と呼ばれる別の種類の境界条件は, 解く変数の値を指定します. 現在の例では, 境界上の1点における温度の値を指定します. この種の境界条件は, 通常, 一意の解を持つ適切問題を設定するために必要です. たとえば, 流体の流れでは, どこかで圧力を指定する必要があります (流れだけでなく). 固体力学では, どこかで変位を指定する必要があります (力だけでなく).

例で見たように, 弱い定式化は境界での熱流束を指定する自然な方法を提供します. では, 境界での固定温度を指定するにはどうすればよいでしょうか?

秘訣は, 自然な境界条件の数学的構造を利用し, テスト関数を使用して解を制限という同じ考え方を適用することです. 概念的には, 境界点で固定温度を維持するには, 境界の外側から来る一定の熱流束が境界内の熱流束を補うために必要です. 弱定式化では, 境界点で固定温度を維持するために必要な熱流束を見つけるという問題が提示されます.

たとえば, 出力流束 \Lambda を x=1 で 2 に指定し, 温度 T を x=5 で 9 に指定する場合, 新しい未知の変数 \lambda_2 とそれに対応するテスト関数 \tilde{\lambda}_2 を導入し, 式を記述します. 式 (6) は次のように表されます:

(7)

ここで, 右側の最初の項は x=1 での 2 の出力流束を指定し, 2番目の項は x=5 での未知の流束を指定します. 両方の項は, 式 (6) の右側の自然境界条件項から直接得られます:

新しい変数 \lambda_2 は, 境界 x=5 で決定される未知の熱流束を表します. 3番目の項は, テスト関数 \tilde{\lambda}_2 によって, x=5 で解が T=9 になるように方程式に追加されます. これは, テスト関数 \tilde{T}(x) に関する以前の説明と同じです.

高次元に関するコメント

これまでは, 非常に単純な1次元の例について説明してきました. 2D 表面領域や 3D 体積領域などの高次元では, 方程式はより複雑になりますが, 基本的な考え方は同じです.

弱定式化により, 微分方程式が積分方程式に変換されます. 部分積分は微分階数を減らして数値的利点をもたらし, 境界での流束を指定するための自然な境界条件を生成します. 単純な 1D の例では, 境界は2つの端点であり, 流束は各点で単一の値です.

2D と 3D では, 境界はそれぞれ領域を囲む閉じた曲線と閉じた面です. 式 (6) の右辺は, 入ってくる流束密度の線積分または面積分, つまり入ってくる流束の合計になります. 本質的に, 2D と 3D の部分積分プロセスでは, 発散定理 を使用して, モデリング領域の境界での流束の線積分または面積分を取得します.

このブログでは, 数学の複雑さによって中心的なアイデアが不明瞭にならないように, 単純な 1D の例を選択しました.

まとめと次のトピック

今日は, テスト関数を使用して解をクランプダウンする弱定式化の考え方について学びました. 弱形式を部分積分すると, 微分階数が減るという数値的な利点が得られます. また, 流束または力 (解く変数の1次導関数) に関して境界条件を指定する自然な方法, いわゆる自然境界条件またはノイマン境界条件も提供されます.

実際の問題を解くときは, 多くの場合, いわゆる固定境界条件またはディリクレ境界条件を介して, 解く変数 (その導関数だけでなく) を指定する必要があります. 弱定式化では, テスト関数とその自然境界条件の同じメカニズムを使用して, 固定境界条件の追加項を構築することを説明しました.

これまでのところ, 方程式は数値近似なしで元の解析形式のままにしています. 次のブログ では, 弱形式方程式 (7) を COMSOL Multiphysics に実装して数値的に解きます. その後, 数値近似が内部でどのように行われるか, 同じ問題をさまざまな方法で解く方法, さまざまなタイプの問題に対してさまざまな境界条件を設定する方法について説明します.