
COMSOL Multiphysics® ソフトウェアは, 偏微分方程式 (PDE) の場の解を求解するためによく使用されますが, 常微分方程式 (ODE) を解く機能もあります. たとえば, 惑星の周りの衛星の動きに関するニュートンの第2法則を解くことができます. この方程式を単独で解くことは非常に簡単であり, この機能をソフトウェアの結果表示機能と組み合わせて, 非常に優れた可視化を行うことができます. もっと学びましょう.
衛星軌道の計算
地球を周回する衛星をモデル化する場合, オブジェクトが受ける重力の式を書くことから始めることができます.
ここで, \phi はポテンシャル関数です.
地球を中心としたデカルト座標系で作業します. 地球がわずかに非球形であるという事実を説明するために, ポテンシャルに対して次の式を使用します.
ここで, \mu_{\oplus} は地球の標準的な重力パラメーター, r は地球の中心から衛星までの距離, J_2 は地球のジオポテンシャルモデルの球面調和関数展開の第2項, P_2 は第2のルジャンドル多項式です.
ポテンシャルの中のこの第2項は, 地球の赤道バルジを説明し, 衛星の歳差運動につながります.
COMSOL Multiphysics に組み込まれている数学関数の1つである legendre() 関数を使用して, この可能性の式を記述できます. 組み込みの sum() 演算子を使用して, ポテンシャル関数に高階項を含めることもできますが, これらは大幅に小さいため, ここでは無視されます.
衛星に重力のみがあると仮定すると, 衛星位置の常微分方程式は次のようになります.
この方程式を解くには, 位置 \mathbf{ {x}}_0, および速度 \mathbf{\dot {x}}_0 の初期条件が必要です. 衛星の位置は, 通常, ケプラリアンの軌道要素で表します. 一般的な楕円軌道の場合, 偏心, \epsilon; 半主軸, a; 傾斜角, \epsilon; 昇交点黄経, \Omega; 近地点引数 \omega は, 楕円を定義します. 真近点角 \nu は, 開始時の楕円に沿った位置を定義します. 昇交点の経度, 傾斜, および近地点引数は, Z-X-Z の適切なオイラー角に対応しており, COMSOL Multiphysics 内の回転系機能を使用して支援することができます. 以下に示すように, この座標系が定義されると, この座標系との間で変換できる9つの行列成分の集合が使用可能になります.
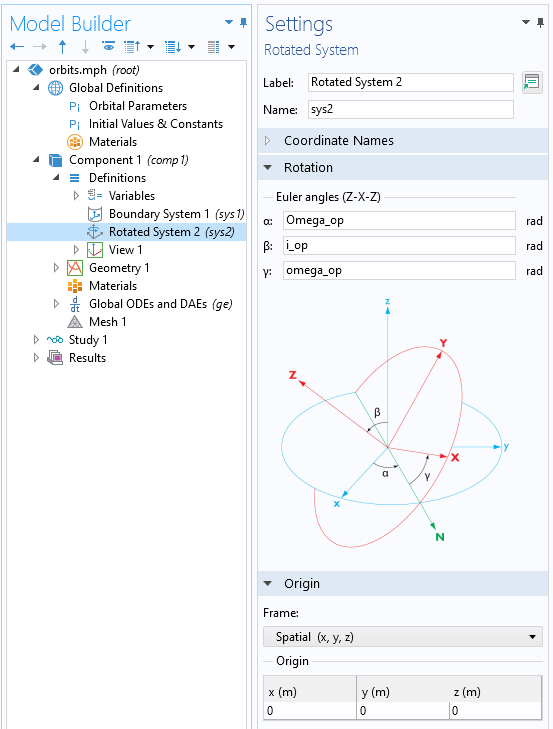
回転座標系機能のスクリーンショット.
たとえば, 最初の真近点角 \nu_0 を昇交点黄経に割り当てると (衛星が赤道を上向きに横切るとき), 軌道面での衛星の初期位置と速度をもう少しだけ計算できます. 次に, 変換行列の成分を使用して, 惑星の中心を基準にしたグローバル座標系の初期位置を取得できます. これで, 完全なモデル定義が得られ, ODE を設定して求解する準備が整いました.
以下のスクリーンショットに示すように, グローバル ODE および DAE インターフェースを使用して, グローバル座標系での位置の方程式を入力できます. 解く変数に t を追加するだけで時間微分がかかり, 2回追加すると2回目の時間微分がかかるため, 式 X_stt は加速度ベクトルの x 成分と同等です. 一方, 重力ポテンシャルなどの式を扱う場合, 微分は d() 演算子を介して行われるため, d(Potential,X_s) は重力の x 成分です.
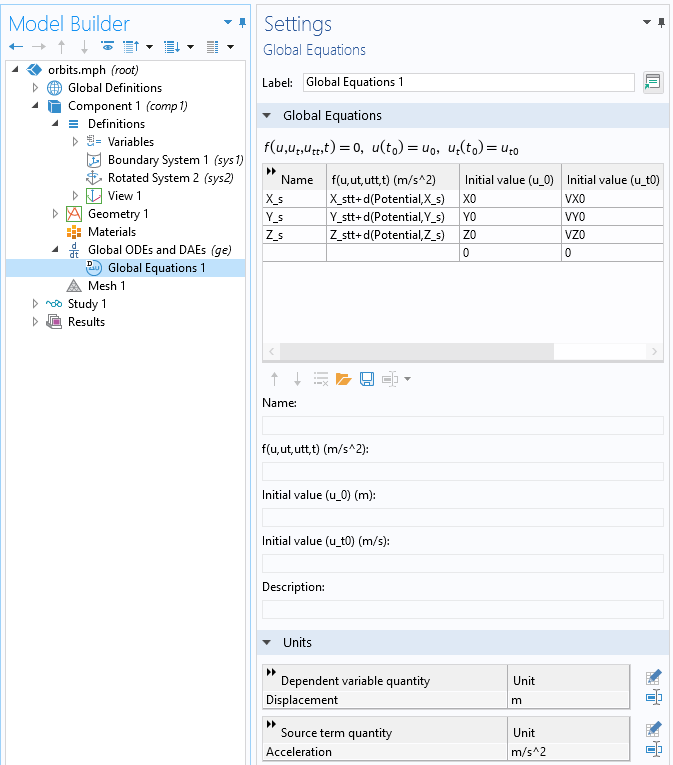
惑星の中心の周りの衛星位置の ODE を解きます. 変数と方程式の単位がどのように設定されているかに注意してください.
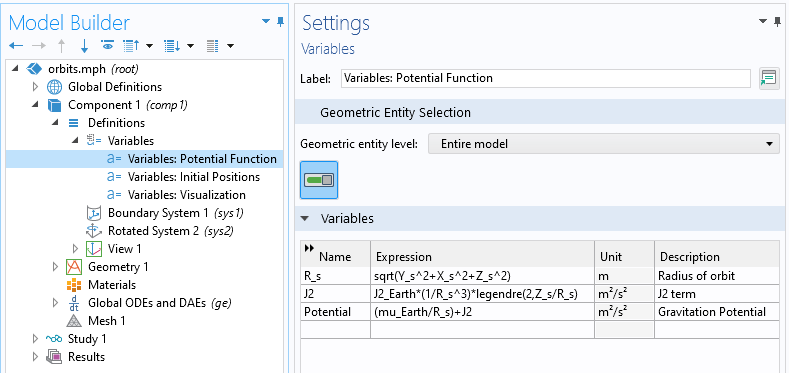
位置の ODE を解くには, 半径と重力ポテンシャルの式を定義する必要があります.
この一連の方程式と ODE は, 任意のタイプの時間依存ソルバーで解くことができますが, タイプに関係なく, 相対的な許容誤差を調べる必要があります. 他のモデリングのニーズによっては, デフォルトの BDF ソルバーが推奨される場合があります. これは, イベント (過渡解の間に方程式の暗黙的にトリガーされる変更) も許可するためです.
軌道の可視化
方程式を解くと, 衛星の位置と高度を時間の経過とともにプロットできます. また, 軌道上にある宇宙船を可視化することもできます. そのために, 次に, 以下に示すように, 宇宙船を表す CAD モデルがあると仮定して, 結果の可視化機能のいくつかを使用する方法を見てみましょう. 示されている一連のベクトルは, 速度に面する方向と天底に面する方向を定義します. これらの2つの単位ベクトルの外積は, 回転座標系機能ですでに説明したように, 軌道面の法線に平行です.
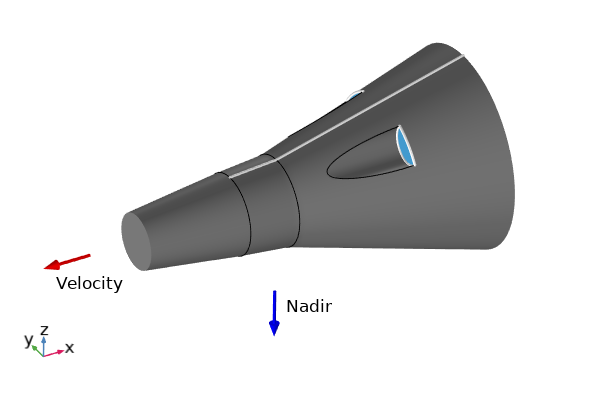
宇宙船の単純な CAD モデルと, CAD 座標系に対して軌道上でどのように方向付けられているかを示すベクトル.
宇宙船をプロットする前に, 私たちが最初にしたいことは, 地球自体の可視化を作成することです. このために, パラメーター化サーフェスデータセットを使用します. これにより, 緯度と経度の観点から球の表現を記述できます.
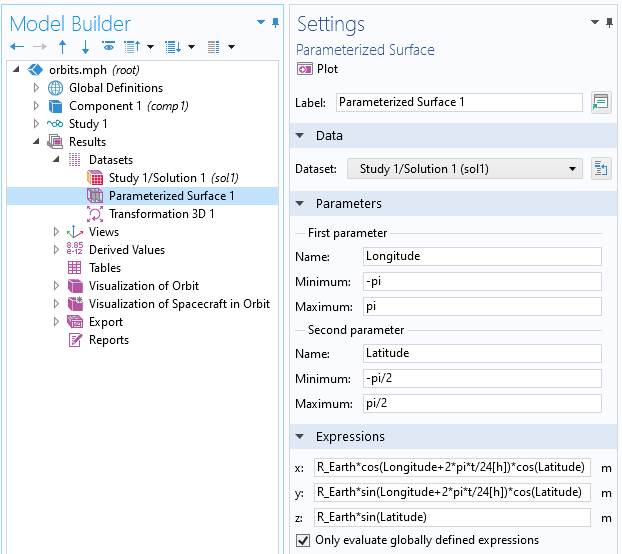
パラメーター化サーフェスデータセット. 球などの単純な式ベースの形状を生成するために使用できます.
これで, 画像プロット機能を使用して, データセットにマッピングされた画像を表示できます. パラメーター化サーフェスは緯度と経度で設定されているため, 以下に示すように, 正距円筒図法を使用した画像をそのサーフェスにマッピングできます.
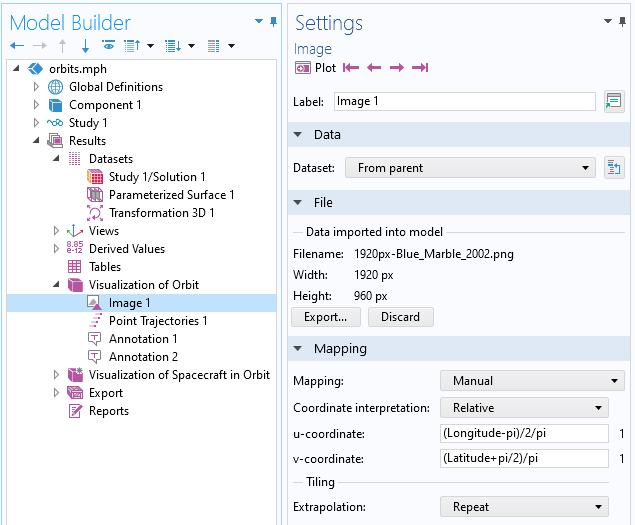
パラメーター化サーフェスデータセットにプロットされた画像データ.
次に, 軌道経路をプロットしたいと思うかもしれません. これは, ポイント軌道プロットタイプを介して実行できます. これにより, 時間の経過に伴う軌道データと宇宙船の位置を入力し, そのパスに沿って線をプロットできます. さらに, 注釈プロットタイプを使用すると, パスに沿って変化する式を評価およびプロットできます.
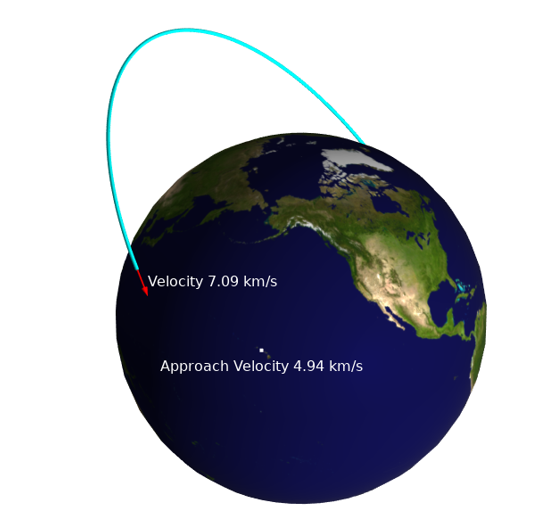
ポイント軌道と注釈プロットを使用して, 衛星の軌道と速度の情報, および地上局に対する速度を可視化します.
最後に, 地球の周りを移動する宇宙船のスケーリングされた可視化をプロットしましょう. これは, 変換3D データセットを介して実行できます. これにより, 地球を中心に宇宙船を適切にスケーリングおよび再配向する一連の基本ベクトルと, 変換ベクトルに関する一般的な変換タイプが可能になります. つまり, 以下に示すように, 速度と天底の方向を定義するベクトルと, 軌道面に垂直なベクトルを使用して, 地球の周りで宇宙船の向きを変えます.
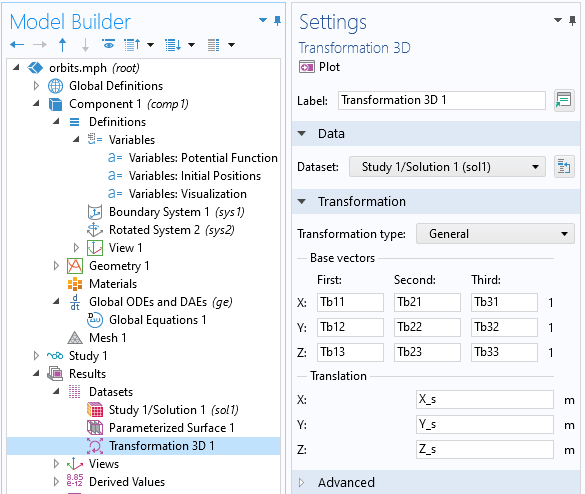
変換3D データセットを使用して, データセットの方向を変えることができます.
惑星の周りを周回している宇宙船のアニメーション.
最後に
惑星の周りの衛星の動きを計算する常微分方程式を解く方法を示しました. 重力ポテンシャル関数にさらに多くの項を含めてそれらの寄与を確認するのは非常に簡単です. また, 軌道減衰につながる大気抗力やその他の要因を説明するために, 追加の力を ODE に追加できます.
あるいは, 物事を単純化するために, この ODE を時間の経過に伴う位置の明示的な方程式に置き換えることができます. ただし, この軌道をどのように計算するかに関係なく, 結果機能を使用して, さまざまな興味深く有用な可視化を作成できます.
お試しください
下のボタンをクリックして, 軌道上で宇宙船をモデリングしてみてください. アプリケーションギャラリのエントリに移動します.
Reto Stöckli 氏による NASA Goddard Space Flight Center の画像 (地表, 海水, 雲). Robert Simmon 氏による画像の補強 (海洋色, コンポジット, 3D 地球, アニメーション). データおよび技術サポート: MODIS Land Group; MODIS Science Data Support Team; MODIS Atmosphere Group; MODIS Ocean Group. 追加データ: USGS EROS Data Center (topography); USGS Terrestrial Remote Sensing Flagstaff Field Center (南極); Defense Meteorological Satellite Program (街灯).


コメント (0)