電気モーターの損失, 温度, 効率の計算

以前, COMSOL Multiphysics® ソフトウェアを用いた電気モーター発電機の設計解析について, 回転機械の磁束分布, トルク, 損失, 鉄の使用量を調べる方法をご紹介しました. ここでは, 直径35mm, 軸長80mmの12スロット, 10極の永久磁石機(PMM) を例に挙げました. このブログでは, 鉄損と銅損の変動, それに伴う温度上昇, PMMの効率への影響を調べます. 今回は損失についてご説明するので, まず回転機シミュレーションの基本であるエネルギー節約の話をします.

本ブログは, COMSOL Multiphysics® を使用して回転機械のさまざまな設計面を解析する方法を説明するシリーズの第2回目です. パート1はこちらから ご覧ください.

電力バランスの検証

エネルギー節約は, 関連する電力値を確認することで検討できます. このためには, 回転機械のシミュレーションにおける電力バランス現象を見てみましょう. 回転機械をモデル化する際には, ステーター鉄とローター鉄の電気伝導度をゼロとし, 鉄損はSteinmetz や Bertotti などの経験的モデルを用いて個別に計算するのが一般的です. これは, ステーターとローターの鉄が積層で構成されており, 渦電流を最小限に抑えることができるためです.

もし, 鉄のバルク導電率を使用した場合, 数値モデルは損失を大幅に過大評価し, 非積層鉄に対応する低い正味磁場を計算してしまいます. そのため, 鉄の損失を個別に計算する必要があるのです. この方法では, 効率は\textrm{Efficiency} = \frac{\textrm{Mechanical output power}}{\textrm{Mechanical output power + iron losses + copper losses}}のように計算できます. ここでは, 摩擦損失と風損は全体の損失のごく一部(約3%)にすぎないことがわかっているため, 無視することにしました. しかし, 必要に応じて, これらの項は簡単に追加することができます.

以上のことから, 電磁場FEMシミュレーションでは, 入力された電力で磁場を励起し, ローターにトルクを発生させ, 銅損を発生させる必要があることがわかります. エネルギー節約の観点からは, 電気エネルギー入力は, 機械的パワー出力と銅損の合計に等しくなければなりません. 瞬時電力はP_i = V_a I_a + V_b I_b + V_c I_cで与えられます. ここでV_a, V_b, V_c とI_a, I_b, I_c はそれぞれステーターの三相電圧と電流です. 機械的出力はP_o = T_r \omega_rで与えられ, ここで, T_rはローターのトルク, \omega_rは角速度です.

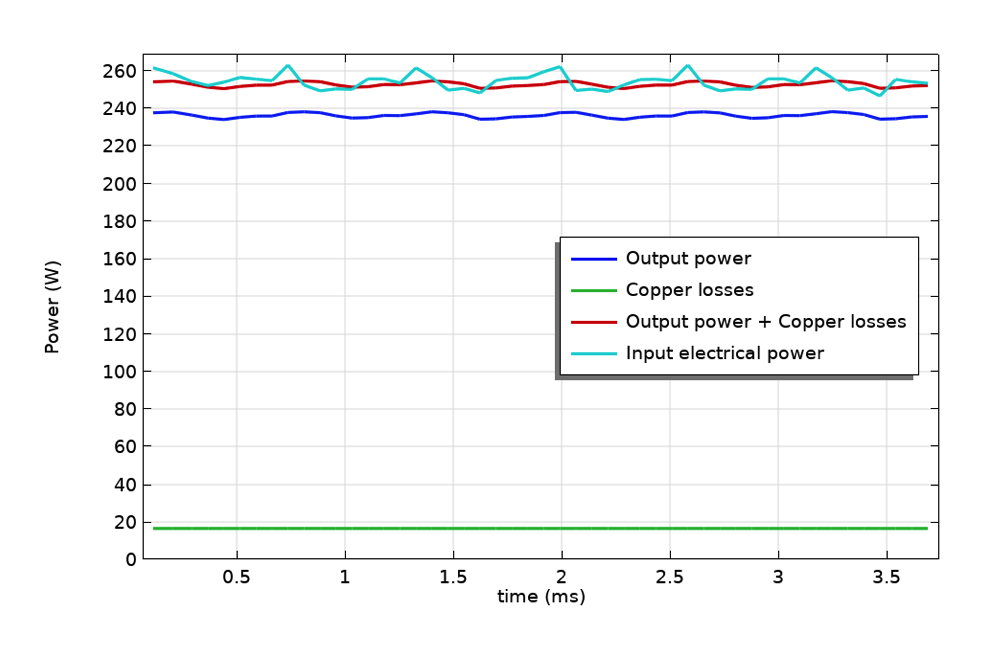
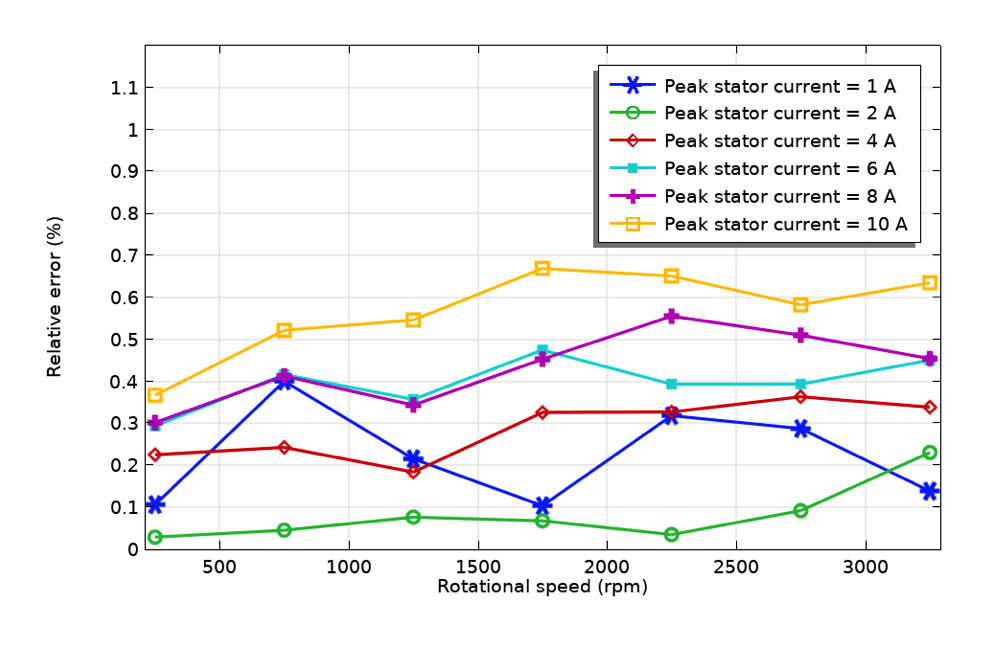
左: ローター回転数3250 rpm, ステーター電流10Aの場合の瞬時電力バランス. 右: 平均電力バランス(入力電力とパワー出力および銅損の合計との間の相対誤差).

瞬時電力バランスは, 機械的パワー出力, 銅損, それらの合計, および電力入力が時間とともにどのように変化するかを観察することによって調べることができます. 電力バランスをさらに調べるために, ローター速度とステーター電流のさまざまな組み合わせについて, 電力入力の時間平均と出力電力および銅損の合計を求めます. 入力電力と出力電力に損失を加えたものとの相対誤差を計算します. 最大相対誤差は, 変動の全範囲にわたって1％未満と評価されます. 電力バランスの検証により, 意図しない損失が発生していないことが確認でき, 回転機開発のツールとしての数値解析に自信が持てるようになりました.

鉄損と銅損の解析

損失の計算は, 効率の計算や温度上昇の評価に重要な意味を持ちます. 鉄損は, 時変磁束密度によるローターとステーターの鉄のヒステリシスと渦電流損失です. 銅損は, 伝導電流が流れることでステーターコイルに発生するオーム損です.

パラメトリックスイープ機能を使って, ローター速度とステーター電流による鉄損と銅損の変化を調べることができます. 損失は, COMSOL Multiphysics® バージョン 5.6 以降のサブ機能である損失計算を用いて計算することができます. 積層鉄については, 経験的な Steinmetz モデルと Bertotti モデルを使用しており, これによって, ヒステリシスと渦電流による総損失が得られます. Bertotti 損失モデルを使用すると, ユーザーはラミネートの厚さの値を指定することができます. また, 独自にカスタマイズされたB-H曲線を備えた, 完全にユーザー定義の材料モデルも利用可能です. また, 異方性などのより高度な効果をシミュレーションに取り入れることも可能です. 銅損は, 損失計算サブ機能の抵抗性損失オプションを使用して得られます(オームの法則に基づく).

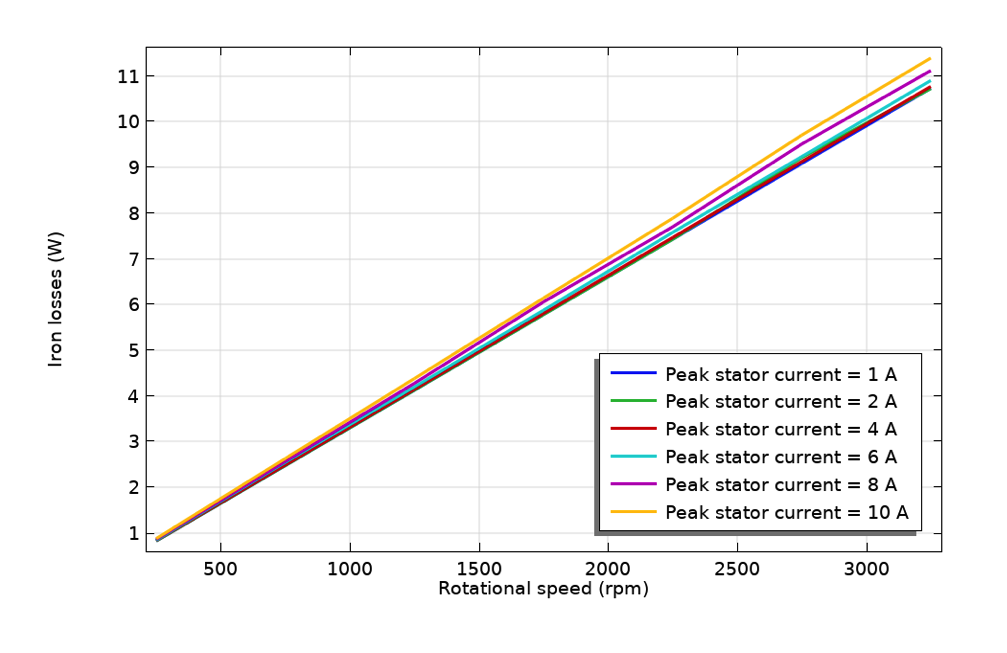
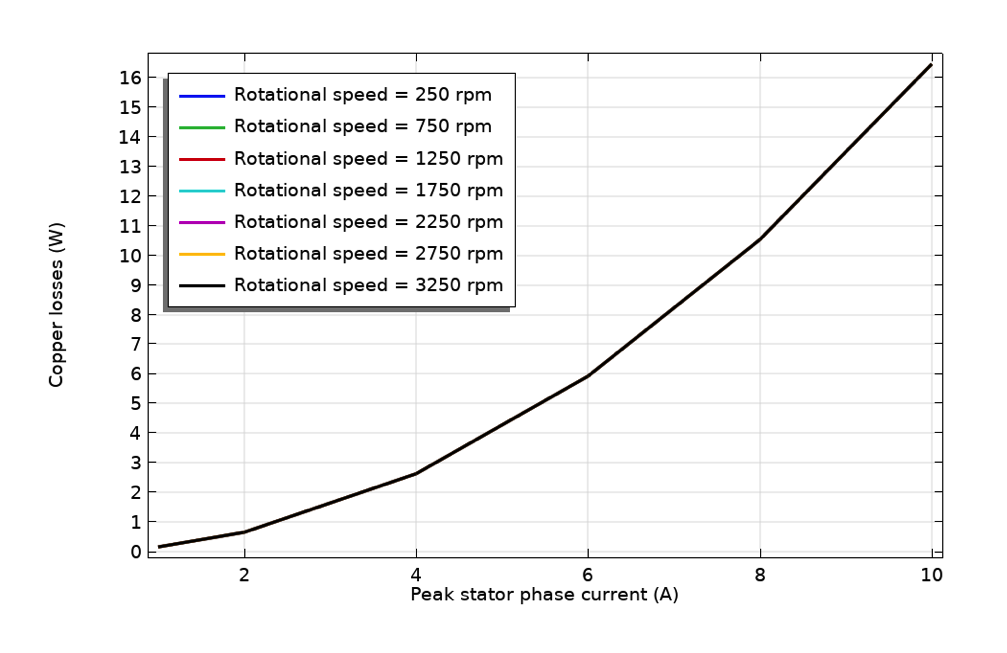
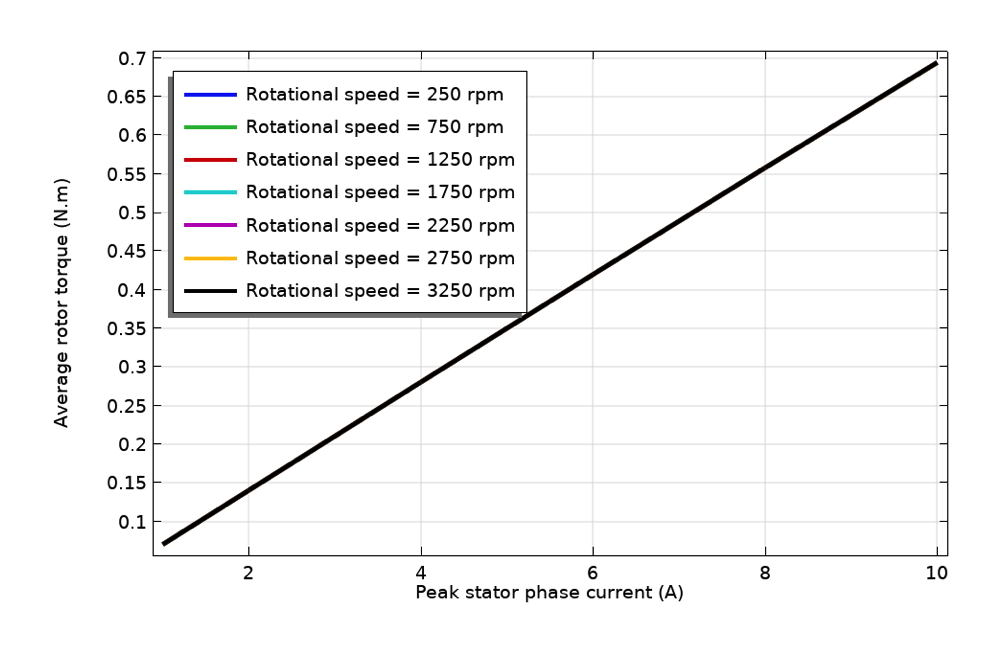
ローター速度による鉄損の変動(左), ステーター電流による銅損の変動(中央), およびステーター電流によるロータートルクの変動(右).

鉄損

鉄損はローター速度に比例して変化し, ステーターの電流に強く依存しません. これは, 経験的損失モデルとの相関で理解できます. 鉄損は, W_i = K_h{B_m}^\alpha fで与えられるSteinmetzの式を使用して計算できます. ここでW_iは単位体積あたりの鉄損, B_mは最大磁束密度, fは磁束密度の変化の周波数です.

この式は, 鉄損が周波数に比例して変化し, 周波数がローター速度に正比例することを示しています. さらに, 鉄の磁束密度は主に磁石によって決定されます. ステーター電流の影響はごくわずかです. その結果, 鉄損はローター速度に比例し, ステーター電流にはほとんど依存しません.

銅損

一方, 銅損はステーター電流に応じて二次関数的に変化することがわかります. この二次変動は, W_c = I^2 R_cで与えられるオーム損失の式を見ると簡単に理解できます. ここで, Iはコイル電流, R_cはコイル抵抗です. この場合, この場合, 一様化マルチターンコイル機能が使用されるため, コイル内の表皮効果と近接効果は無視されます. これは, ワイヤーが表皮厚よりも薄い場合に有効な仮定です. したがって, 実効的なR_cはローター速度に依存しません.

ロータートルク

また, ステーター電流によるロータートルクの変化を調べて, 与えられたモーター設計のトルク定数を求めることもできます. トルクはステーター電流に比例し, 速度には比較的依存しません. トルクは, ステーター電流とローター磁場の相互作用によって生成されます. PMMの場合, ローターの磁場は永久磁石によって生成されます. 多くの典型的な設計では, これは本質的に一定であると考えることができます. したがって, 電磁トルクはステーター電流によってのみ変化することが簡単に理解できます.

ローターのトルク, 鉄損, および銅損に対するローターの速度とステーター電流のプロットを使用して, 経験的な関係を取得し, モーターの効率マップを作成することができます. ロータートルク定数, 鉄損, 銅損, および効率に対応する式は次のとおりです.

ここでは, k_1 = 0.07 N.m/A, 平均的な傾きはk_2 = 0.204 W/rps, k_3 = 0.164 W/A²です.

経験的な係数(k_1,k_2,k_3)を用いて解析的に作成した効率マップと, モーターモデルのパラメトリック解析から得られた効率マップを比較すると, 興味深いでしょう.

COMSOL Multiphysics® による温度上昇の解析

温度上昇は, モーター性能のいくつかの側面に影響を与えます. 永久磁石の場合, 温度が例えば20度から120度に上昇すると, 磁束密度が最大で30％低下します. これに伴い, ローターのトルクが低下し, 結果として効率も最大で30％低下します. 最大許容温度上昇は, 通常, ステーター巻線の絶縁クラスと永久磁石材料の減磁限界を考慮して決定されるのが一般的です. 経験的には, 許容限界を超えて温度が10度上昇するごとに, 絶縁寿命が半分になることがわかっています. 極端な負荷条件下で温度が絶縁限界を超えると, 絶縁不良, ターン間短絡, 最終的にはステーターコイルの焼損につながる可能性があります.

損失計算サブ機能を使用して計算された鉄および銅の損失は, 熱伝達(HT)インターフェースに連結して熱性能を解析することができます. COMSOL Multiphysics® の伝熱インターフェースには, 機械の冷却を調べるためのいくつかの方法があります. 自然対流または強制対流は, 外面からの熱伝達係数を使用して暗黙的にモデル化することも, モーターの外面上の層流または乱流の流体の流れをモデル化することによって陽にモデル化することもできます. また, 特定のモーターアプリケーションに最適な冷却方法を特定するために, 定常状態温度の比較スタディをさまざまな冷却条件下で行うことも良いでしょう. 水冷ジャケットの最適な設計など, モーターの冷却については, 今後のブログで詳しくご紹介します.

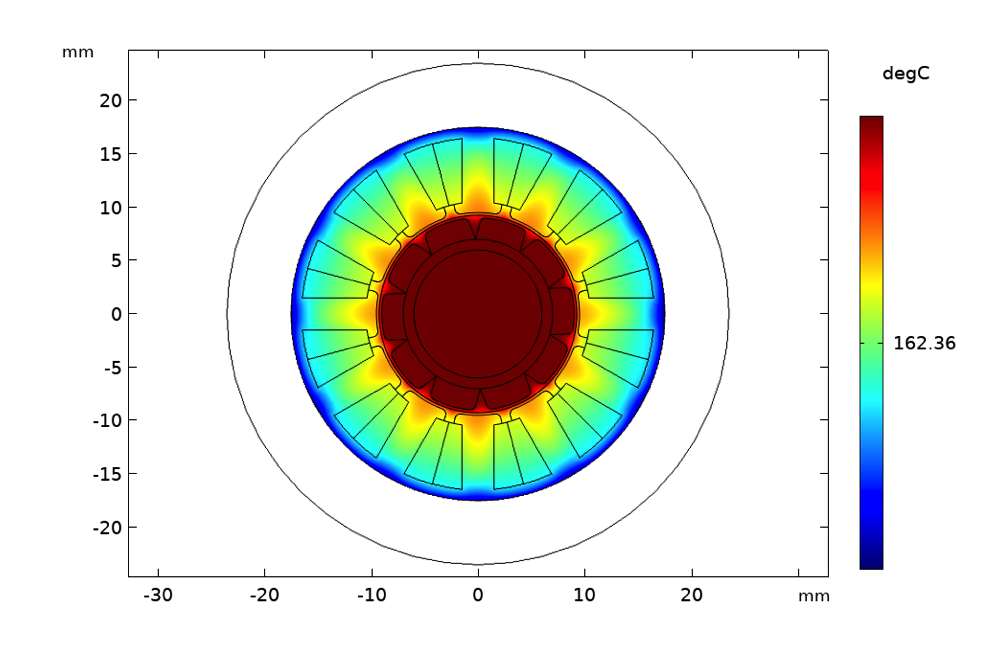
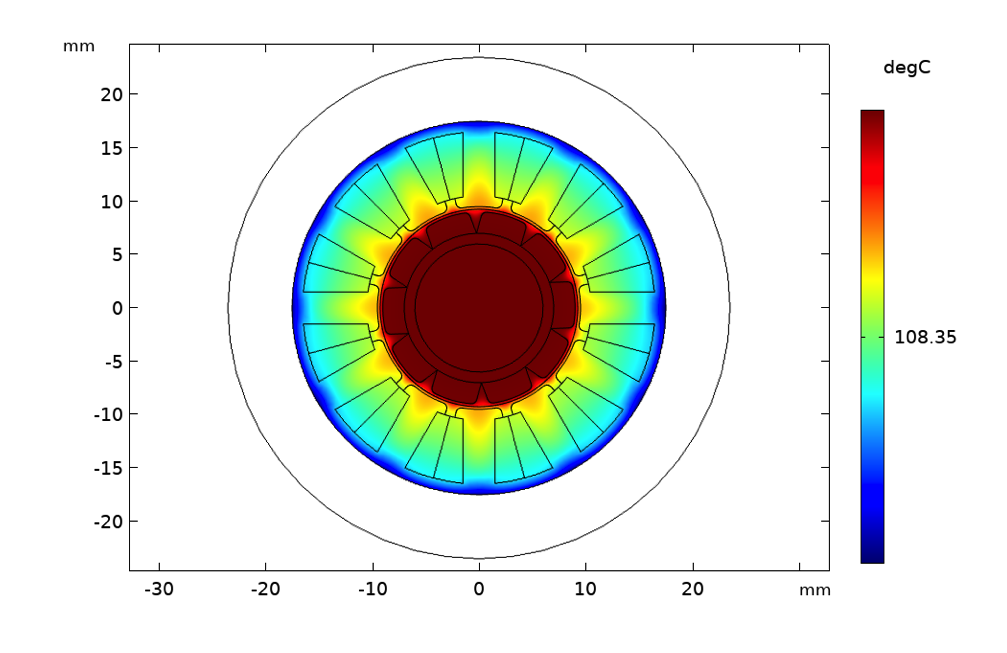
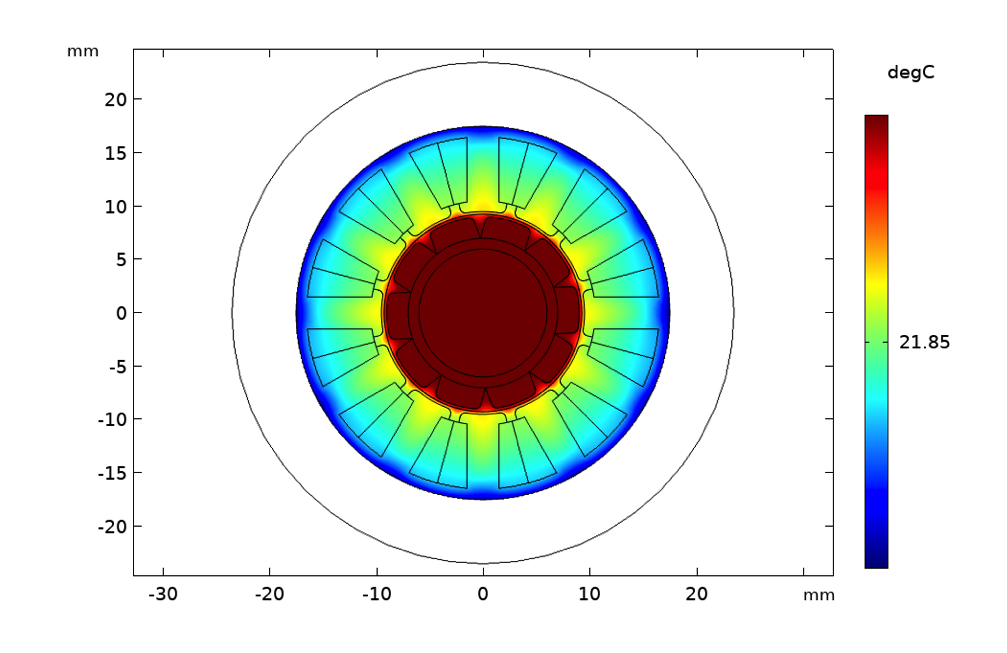
自然対流による温度上昇(左), 流速1 m/sの強制空気対流(中央), 流速50 mm/sの強制水冷(右).

表面プロットは, ローター速度が3000 rpm, ステーター電流が2Aの場合の温度を度単位で示しています. この場合, 見るだけで, 自然対流を使用する場合は絶縁クラス180 (H)が必要であると判断できます. 強制対流を使用する場合は, 必要な絶縁材はクラス130 (B) に減り, 水冷の場合はクラス105 (A) の絶縁材で十分です. ここでは, ここでは, 永久磁石の材質が熱減磁効果を考慮して適切に選択されていることを前提としています.

電気モーターの効率解析

モーターの設計を解析することは, 最終的には効率を求めることになります. 効率とは, 入力された動力の何割が機械的な出力として得られるかを示すものです. 回転機の効率は, 発生する電磁トルクとローター速度によって変化します. 理想的には最大効率で運転することが望ましいのですが, 実際にはモータで駆動する負荷のトルク・速度曲線も考慮しなければなりません. その結果, モーターはある一定の動作範囲で使用されることになります. 次善の策としては, その動作領域で最高の効率値を持つモータを選択することです.

そこで登場するのが「効率マップ」です. モーターの効率マップとは, ローター速度と電磁トルクの変化に対する効率をプロットしたものです. 言い換えれば, トルクと速度の状態空間における効率のプロットとも言えます. この効率マップに負荷特性曲線を重ね合わせることで, 与えられた負荷曲線に対するシステムの総合効率を求めることができます.

例えば, 電気自動車の負荷は, トルクと速度のドライブサイクルで与えられます. ドライブサイクルは, 負荷のトルクと速度の時間変化で構成されています. 各時点で, トルクと速度の値の組み合わせが負荷の挙動を指定します. このようなトルク・速度のデータポイントを効率マップに散布することで, 特定のドライブサイクルに対してモーターがどのような総合効率を示しているかを知ることができます. これにより, ドライブサイクル全体でモーターが消費するエネルギーの総量を推定することができ, 1回の充電での電気自動車の航続距離を予測することができるのです.

COMSOL Multiphysics は, モーター設計の効率マップを簡単に作成できるモデリング機能を備えています. 力計算で, 電磁トルクを求めることができ, 損失計算サブ機能では, 鉄損と銅損を求めることができます. また, 伝熱インターフェースを使用して, 損失による温度上昇を計算することも可能です. このインターフェースは, 温度上昇の電磁効果を含めるために, マルチフィジックスノードを使用して回転機械, 磁気インターフェースと完全連成することができます. 最後に, テーブルグラフ機能を使って, 効率マップをプロットします.

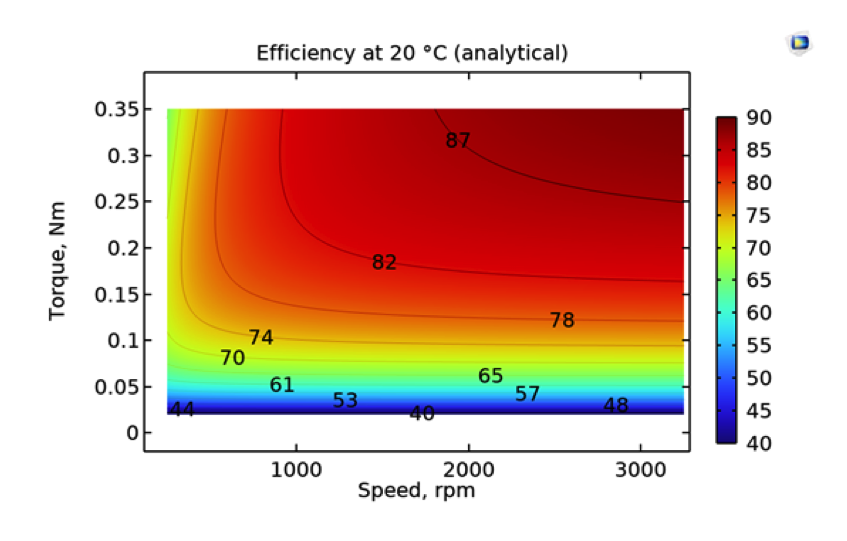
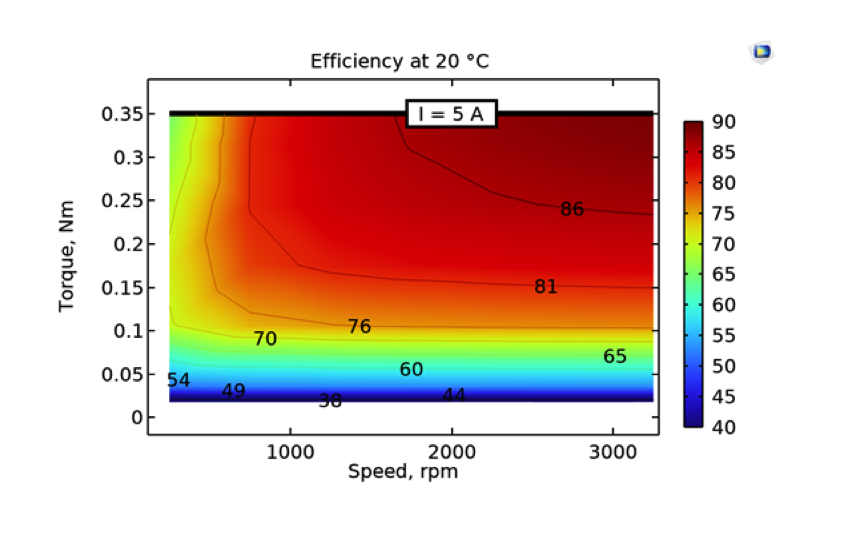
経験的な係数を用いて解析的に作成した効率マップ(左)と, パラメトリックシミュレーションで得られた効率マップ.

ここでは, すべての効率マップがパーセント効率を示しています. 最初の効率マップは, 最初のセクションで詳しくご説明したように, 解析的に作成されました. 2つ目の効率マップは, パラメトリック解析から直接得られたものです. プロットの上部にある水平線は, 最大トルクが5Aのステーター電流に対応することを示しています. 解析的な効率マップと数値的な効率マップは, 妥当な一致を示していると言えるでしょう.

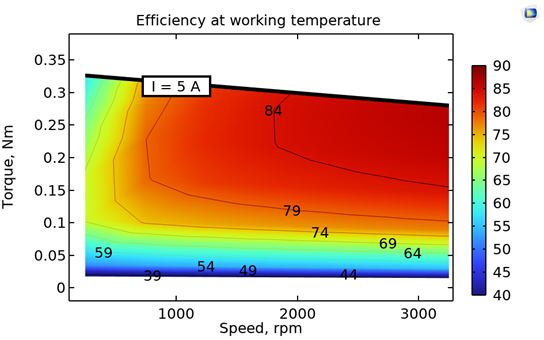
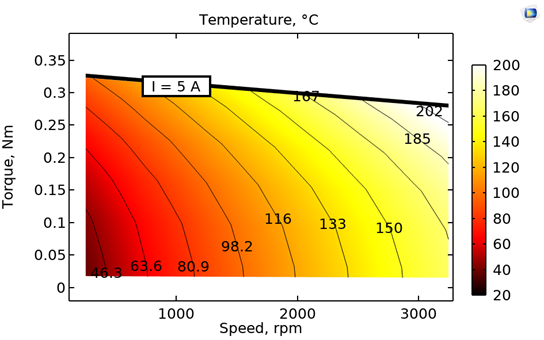
温度上昇の影響(左)とモータの温度マップ(右)を含めた, シミュレーションから得られた効率マップ.

最初の2つの効率マップとは異なり, 3つ目のマップでは, 自然空冷による温度上昇の影響が含まれています. 温度上昇の影響を考慮すると, 同じ範囲のステーター電流値に対する平均ロータートルク値が減少していることがわかります. さらに, (損失の増加により)高速で温度が上昇すると, ローターの永久磁石の残留磁束が減少するため, トルクはさらに減少します. これは, プロットの上部にあるI = 5Aに対応する線をたどるとわかります. 結果として, 温度上昇による効率分布の変化が見られます. これは, あるモータ設計が対象となるアプリケーションに適しているかどうかをよりよく評価するのに役立ちます. 温度マップは, 平均ステーター温度を示しています. これは, モーターの動作に関連する領域に焦点を当てることで, 必要な絶縁クラスや永久磁石の材質の決定を容易にするのです.

最後に

今回は, モーターシミュレーションにおけるエネルギーバランスについて簡単にご説明しました. このような電力バランス検証は, あらゆるFEMシミュレーションツールから得られた結果のチェックを行うのに役立ちます.

パラメトリック解析は, 電磁トルクの変動やローター速度とステーター電流による鉄と銅の損失を調べるために使用できます. このような解析は, トルク定数と経験的な係数を抽出するために使用することができ, 与えられたモーター設計の任意の速度と電流値における損失を推定することができます.

電磁トルク, 効率, 必要な絶縁クラス, 永久磁石の材質に大きな影響を与える, モーターの損失による温度上昇について調べてみました. さまざまな冷却条件下での温度上昇の比較スタディを使用すると, 適切な冷却方法を簡単に選択できます.

最後に, あるモーターの設計がアプリケーションのニーズを満たしているかどうかを判断するための重要なツールである効率マップについてお話しました. 温度上昇を考慮した上で効率マップを確認することで, 用途に応じた機械の性能をより詳細に判断することができます.

自分で試す

電気モーターの損失, 温度, 効率をご自分で計算してみましょう. 下のボタンをクリックすると, ここで取り上げたモデルのMPHファイルにアクセスできます.