
このブログでは, 共役熱伝達 の概念を説明し, その応用例をいくつか紹介します. 共役熱伝達は, 固体の熱伝達と流体の熱伝達の組み合わせに対応します. 固体では伝導が優勢であることが多いのに対し, 流体では通常対流が優勢です. 共役熱伝達は多くの状況で見られます. たとえば, ヒートシンクは, ヒートシンク内の伝導による熱伝達と周囲の流体の対流を組み合わせるように最適化されています.
固体と流体による熱伝達
固体内の熱伝達
ほとんどの場合, 固体内の熱伝達は, 伝導のみによる場合, 伝導熱流束 q が温度勾配に比例するフーリエの法則によって説明されます: q=-k\nabla T.
時間依存問題の場合, 不動の固体内の温度場は, 次の形式の熱方程式を検証します:
流体内の熱伝達
流体の動きにより, 熱方程式への3つの寄与が含まれます:
- 流体の輸送はエネルギー輸送も意味し, これは対流寄与として熱方程式に現れます. 流体の熱特性と流れの状態に応じて, 対流熱伝達または伝導熱伝達のいずれかが優勢になる場合があります.
- 流体の流れの粘性効果により, 流体が加熱されます. この項は無視されることが多いですが, 粘性流体の高速流れではその寄与が顕著です.
- 流体の密度が温度に依存するとすぐに, 圧力仕事項が熱方程式に寄与します. これは, たとえば空気を圧縮すると熱が発生するというよく知られた効果を説明しています.
伝導に加えてこれらの寄与を考慮すると, 流体の温度場に関する次の過渡熱方程式が得られます:
共役熱伝達アプリケーション
効果的な熱伝達
流体と固体の熱伝達を効率的に組み合わせることが, 効果的な冷却器, 加熱器, または熱交換器を設計する鍵となります.
流体は通常, 長距離でエネルギーキャリアの役割を果たします. 強制 対流 は, 高い熱伝達率を実現する最も一般的な方法です. 一部のアプリケーションでは, 対流と相変化 (たとえば, 液体の水から蒸気への相変化) を組み合わせることで, パフォーマンスがさらに向上します.
それでも, 特に熱交換器で流体を分離して, 流体が混ざることなくエネルギーを交換できるようにするには, 固体も必要です.
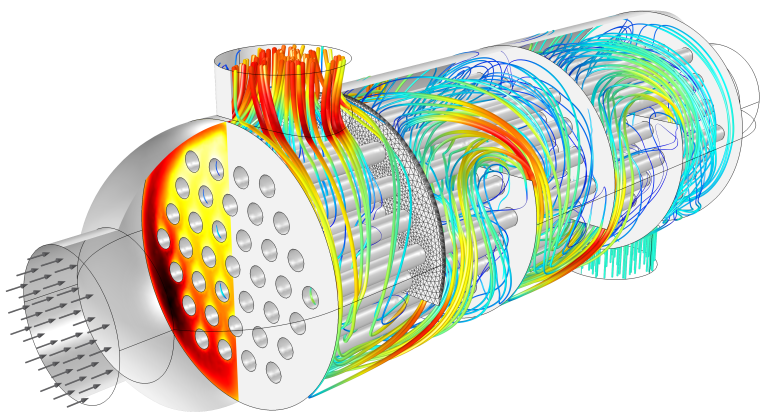
シェル‐チューブ型熱交換器 の流れ場および温度場. 薄い金属壁で分離された2つの流体間の熱伝達を示しています..
ヒートシンクは通常, 熱伝導率の高い金属 (銅やアルミニウムなど) で作られています. ヒートシンクは, 固体部分と周囲の流体間の交換面積を増やすことで熱を放散します.

電源ユニット内の温度場は, 排気ファンと穴あきグリル によって生成される空気の流れによって冷却されます. 2つのアルミニウムフィンは, 空気の流れと電子部品の間の交換面積を増やすために使用されます.
エネルギーの節約
流体と固体の熱伝達を組み合わせることで, さまざまなデバイスでの熱損失を最小限に抑えることもできます. ほとんどのガス (特に低圧の場合) は熱伝導率が小さいため, 熱絶縁体として使用できます. ただし, ガスが動いていない場合に限ります. 多くの場合, ガスは軽量であるため, 他の材料よりも好まれます. いずれにしても, 対流による熱伝達を制限することが重要です. 特に, 自然対流の影響を減らすことが重要です. 壁を慎重に配置して小さな空洞を使用すると, 自然対流を制御できます. この原理をマイクロスケールに適用すると, 断熱フォームの概念が生まれます. この概念では, 小さな空気の空洞 (気泡) がフォーム材料 (ポリウレタンなど) に閉じ込められ, 高い断熱性能と軽量性が組み合わされています.
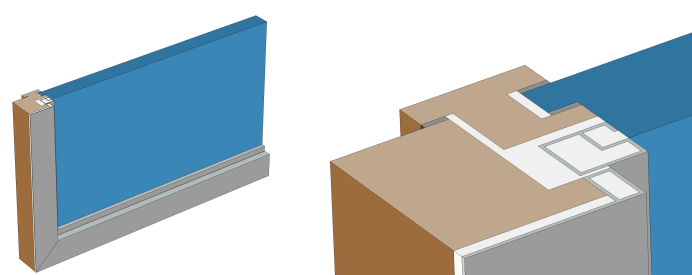
窓の断面 (左) と窓枠の拡大図 (右).
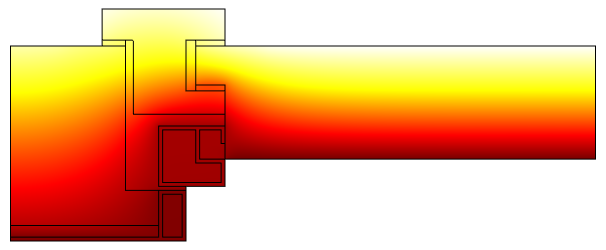
ISO 10077-2:2012 の窓枠と窓ガラスの断面の温度プロファイル (熱性能ウィンドウ).
流体と固体の相互作用
流体/固体のインターフェース
流体/固体のインターフェースでは, 温度場と熱流束は連続しています. ただし, 流体が動いているときは温度場が急激に変化することがあります. 固体に近い場合は, 流体の温度は固体の温度に近くなり, 界面から遠い場合は, 流体の温度は入口または周囲の流体の温度に近くなります. 流体の温度が固体の温度から流体のバルク温度まで変化する距離は, 熱境界層 と呼ばれます. 熱境界層のサイズと運動量境界層の相対的なサイズは, プラントル数 (Pr=C_p \mu/k) によって反映されます. プラントル数が 1 になるには, 熱境界層と運動量境界層の厚さが同じである必要があります. 運動量層が厚いほど, プラントル数は 1 より大きくなります. 逆に, プラントル数が 1 より小さい場合は, 運動量境界層が熱境界層より薄いことを示します. 大気圧および 20°C の空気のプラントル数は 0.7 です. これは, 空気の場合, 運動量境界層と熱境界層のサイズはほぼ同じですが, 運動量境界層は熱境界層よりわずかに薄いためです. 20°C の水の場合, プラントル数は約 7 です. したがって, 水中では, 壁に近い温度変化は速度変化よりも急激です.
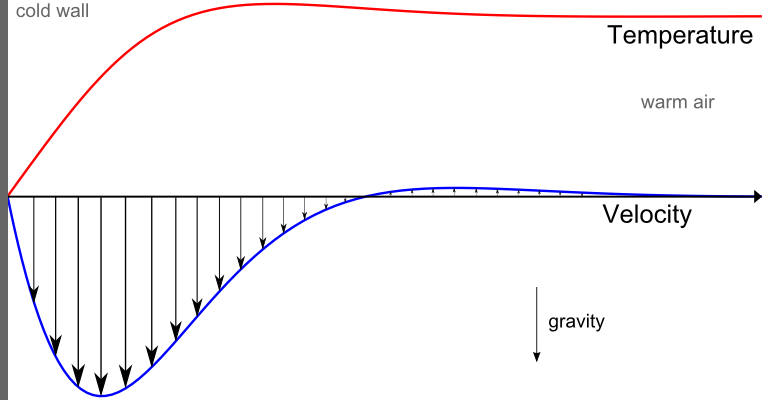
冷たい固体壁に近い空気の自然対流の正規化された温度 (赤) と速度 (青) のプロファイル.
自然対流
自然対流の領域は, 流れが浮力効果によって駆動される構成に対応します. 予想される熱性能に応じて, 自然対流は有益 (冷却用途など) または有害 (断熱層内の自然対流など) になる場合があります.
Ra と表記されるレイリー数は, 自然対流によって誘発される流れの状態と, その結果生じる熱伝達を特徴付けるために使用されます. レイリー数は, 流体材料の特性, 典型的なキャビティサイズ L, および通常は流体を取り囲む固体によって設定される温度差 \Delta T から定義されます:
グラスホフ数は, 浮力と粘性力の比率を示す別の流動状態指標です:
レイリー数は, 関係 Ra=Pr Gr を通じてプラントル数とグラスホフ数で表すことができます.
レイリー数が小さい場合 (通常 <103), 対流は無視でき, 熱伝達のほとんどは流体の伝導によって発生します.
レイリー数が大きい場合, 対流による熱伝達を考慮する必要があります. 浮力が粘性力に比べて大きい場合, 状態は乱流になり, そうでない場合は層流になります. これら2つの状態間の遷移は, グラスホフ数の臨界次数 109 で示されます. 固体壁と流体バルク間の温度遷移の一般的な距離を与える熱境界層は, \delta_\mathrm{T} \approx \frac{L}{\sqrt[4\,]{Ra}} で近似できます (Pr が 1 以上のとき).

熱い表面と接触している コップ一杯の冷たい水の中の自然対流 によって誘発される温度プロファイル.
強制対流
強制対流領域は, 浮力効果を支配する外部現象 (風など) またはデバイス (ファン, ポンプなど) によって流れが駆動される構成に対応します.
この場合, 流れの状態は, 等温流れと同様に, レイノルズ数を指標として使用して特徴付けることができます. Re= \frac{\rho U L}{\mu}. レイノルズ数は, 慣性力と粘性力の比を表します. レイノルズ数が低い場合, 粘性力が優勢になり, 層流が観察されます. レイノルズ数が高い場合, システム内の減衰は非常に低く, 小さな乱れが生じます. レイノルズ数が十分に高い場合, 流れ場は最終的に乱流状態になります.
運動量境界層の厚さは, レイノルズ数を使用して, \delta_\mathrm{M} \approx \frac{L}{\sqrt{Re}} で評価できます.
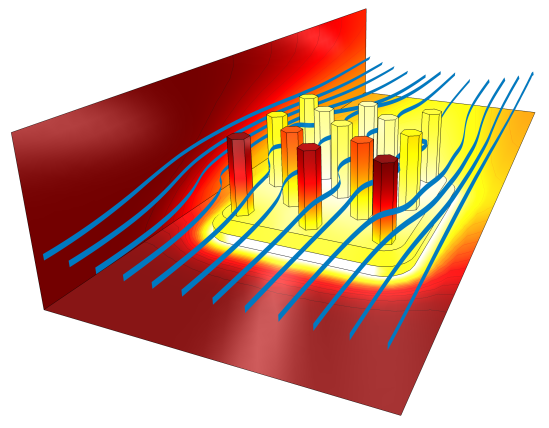
強制対流による冷却 ヒートシンク 周辺の流線と温度プロファイル.
輻射熱伝達
輻射熱伝達は, 上記の伝導熱伝達および対流熱伝達と組み合わせることができます.
ほとんどのアプリケーションでは, 流体は熱輻射に対して透明で, 固体は不透明です. その結果, 輻射による熱伝達は, 透明な空洞を通して固体壁の間でエネルギーを伝達する表面間輻射として表すことができます. 拡散した灰色の表面から放出される輻射熱流束は, \varepsilon n^2 \sigma T^4 に等しくなります. 表面が均一な T_\mathrm{amb} にある物体に囲まれている場合, 正味の輻射流束は q_\mathrm{r} = \varepsilon n^2 \sigma (T_\mathrm{amb}^4-T^4) です. 周囲に異なる温度の表面がある場合, 各表面間の交換は表面の形態係数によって決まります.
ただし, 流体と固体はどちらも透明または半透明である可能性があります. したがって, 輻射は流体と固体で発生する可能性があります. 関与する (または半透明の) 媒体では, 輻射線は媒体 (固体または流体) と相互作用し, 輻射線を吸収, 輻射, 散乱します.
輻射熱伝達は, 温度差が小さく放射率が低いアプリケーションでは無視できますが, 温度差が大きく放射率が大きいアプリケーションでは重要な役割を果たします.
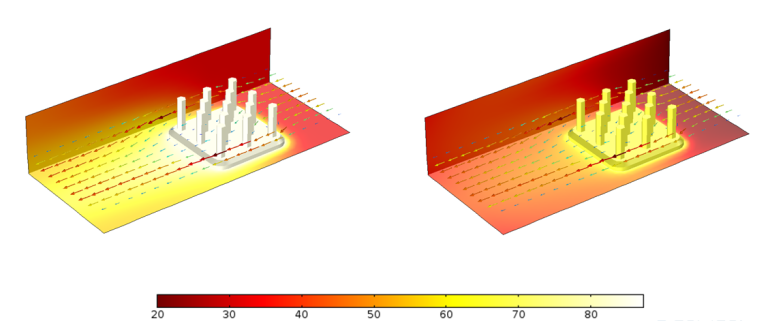
表面放射率を持つヒートシンクの温度プロファイルの比較 \varepsilon = 0 (左) および \varepsilon = 0.9 (右).
結論
固体の熱伝達と流体の熱伝達は, ほとんどのアプリケーションで組み合わされています. これは, 流体が固体の周囲または固体の壁の間を流れ, 固体が通常流体に浸されているためです. 熱伝達モード, 材料特性, 流動様式, および幾何学的構成を正確に記述することで, 温度場と熱伝達を分析できます. このような記述は, 共役熱伝達効果を予測したり, たとえば特定のアプリケーションの熱性能を向上させるためにさまざまな構成をテストしたりするために使用できる数値シミュレーションの出発点でもあります.
表記
C_{p}: 定圧時の熱容量 (SI 単位: J/kg/K)
g: 重力加速度 (SI 単位: m/s2)
Gr: グラスホフ数 (無次元数)
k: 熱伝導率 (SI 単位: W/m/K)
L: 特性寸法 (SI 単位: m)
n: 屈折率 (無次元数)
p_\mathrm{A}: 絶対圧力 (SI 単位: Pa)
Pr: プラントル数 (無次元数)
q: 熱流束 (SI 単位: W/m2)
Q: 熱源 (SI 単位: W/m3)
Ra: レイリー数 (無次元数)
S: ひずみ速度テンソル (SI 単位: 1/s)
T: 温度場 (SI 単位: K)
T_\mathrm{amb}: 周囲温度 (SI 単位: K)
\bold{u}: 速度場 (SI 単位: m/s)
U: 典型的な速度の大きさ (SI 単位: m/s)
\alpha_{p}: 熱膨張係数 (SI 単位: 1/K)
\delta_\mathrm{M}: 運動量境界層の厚さ (SI 単位: m)
\delta_\mathrm{T}: 熱層の厚さ (SI 単位: m)
\Delta T: 特性温度差 (SI 単位: K)
\varepsilon: 表面放射率 (無次元数)
\rho: 密度 (SI 単位: kg/m3)
\sigma: シュテファン・ボルツマン定数 (SI 単位: W/m2T4)
\tau: 粘性応力テンソル (SI 単位: N/m2)






コメント (0)