流体の計算モデリングにおける問題のひとつに, 実験との相関性の問題があります. 数値結果の美しい3D 可視化は非常に簡単ですが, これらを実験結果と比較することは, 困難な場合が多いのです. 実験手法のひとつに, 3D の流れ場の2D 画像を生成するシュリーレンイメージングがあります. 実は, COMSOL Multiphysics® ソフトウェアを使用すると, このようなイメージングの可視化を非常に簡単に作成できます. 詳しく学んでいきましょう.
シュリーレンイメージングの背景
シュリーレンというイメージング技術の歴史は古く, 文字で書かれた歴史よりも古いかもしれません. 古代の砂漠や海を旅する人々は, 遠方に移るファタモルガナや逆さ帆船など, 蜃気楼の概念に精通していました (これが空飛ぶオランダ人などの寓話につながったのかもしれません). これらの現象は, 光線が密度の異なる空気の中を通過する時に, わずかに曲がるために発生します. これは, 1000年以上前から何らかの形で解明されていたと思われますが, 実験技術が開発されたのは, ここ500年ほどのことです.
シュリーレンイメージング法には様々なバリエーションがありますが, 基本的な動作原理は非常に単純です. 流体 (または固体) 内の温度や圧力の変化は, 密度の局所的な変化をもたらし, その密度は屈折率に影響を与えます. 大気中の空気の場合, 密度 \rho に対する屈折率 n のグラッドストーン・デール関係は次のようになります.
ここで, 可視光線の場合, G は約0.23 cm 3 /g です.
なお, 上記の式は単純な出発点であり, より完全な式も利用可能であり, 混合ガスや反応流の場合はさらに複雑な式が存在します. 実験手法の目的は, このような流れの中の密度変化の光学画像を作成することです.
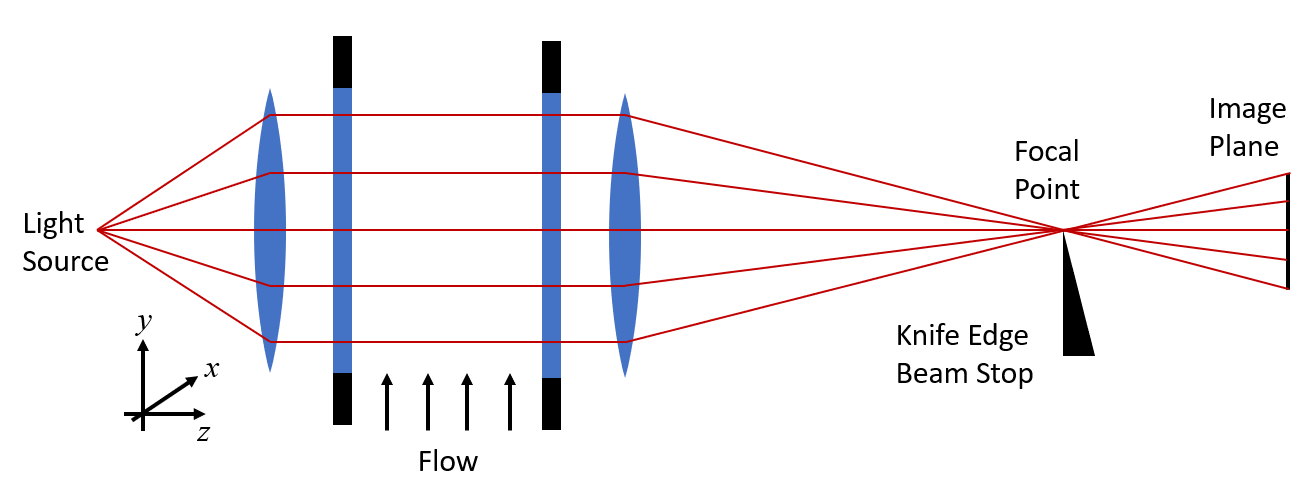
シュリーレンイメージングの設定.
典型的な実験装置を上の模式図に示します. 風洞の側面にあるような2つの透明な窓が, 流れ場を囲んでいます. まず, 流れに変動がないことを仮定します. 片側に光源があり, 均一な照明を与えるいくつかの光学素子 (レンズまたは鏡) があります. 幾何光学的なアプローチにより, この光を, 流れを通過し, 次に光を画像平面に集束させる別の光学要素の集合を通過する平行光線の集合として扱います.
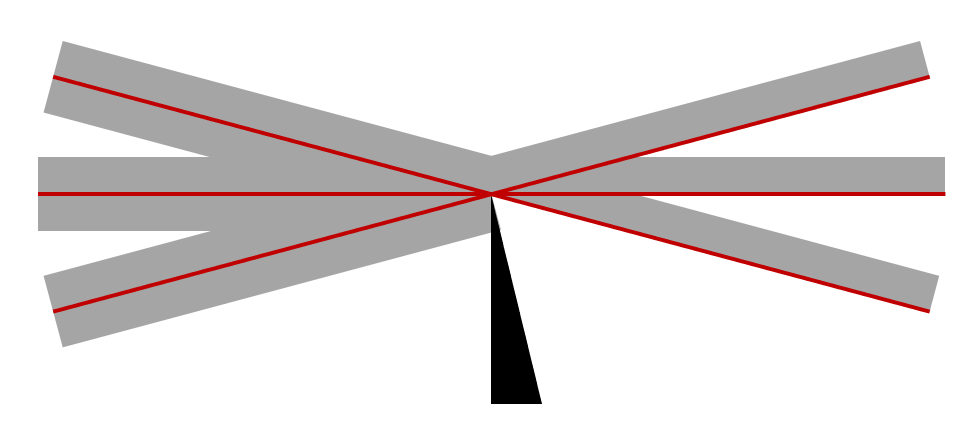
焦点位置での乱れのない光線. ナイフエッジは光の半分を遮断し, エッジでの回折は無視されます.
しかし, ここで重要なのは, いわゆる焦点は一点ではない, ということです. 光は一点に集光することはできず, 集光されたビームには必ず有限の半径が存在するのです. この点を理解するには, 波動電磁気学を理解する必要があります.
しかし, 私たちの目的には, ある重要な点さえ理解していれば, 幾何光学的なアプローチで十分です. それは, 焦点位置に置かれた障害物は, 光の一部を遮るということです. もし, この位置にナイフエッジ (実験的にはカミソリの刃) を置くと, 全体の半分の光を遮りながら (それでも半分の強度ではありますが), 完全な画像が得られます. これを理解するための一つの方法として, 上の画像のように, それぞれの光線がある有限の厚さを持つものと考えることができます (この考え方は, この概念を理解するためにのみ役立ちますが).
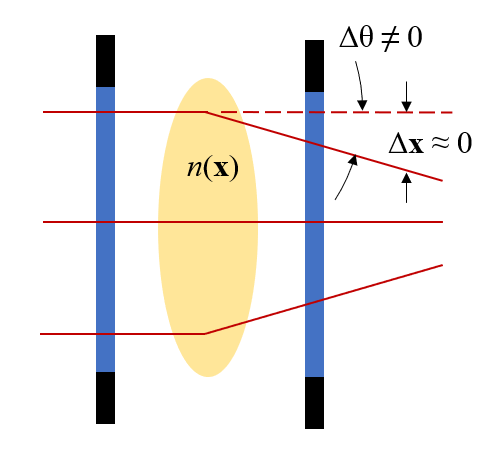
屈折率がわずかに変化する領域では, 光線の方向はわずかに変化しますが, 出射面における位置は変化しません.
では, 流れの中に密度の変動があるとどうなるかを考えてみましょう. 屈折率が密度の関数であることは既にわかっているので, 回路図に小さな屈折率の変化を導入して, 何が起こるかを見てみましょう. 上の図に, 重要な挙動を示しました. ここでは, 全体の導出を省略し, 次の点を強調することにします.
- xy 平面上の屈折率が変化すると, ビームは z 方向に伝搬する際にごくわずかに方向 (角度) を変える
- 光線が実験ドメインを通過する際の, xy 平面上での位置の変化はごくわずかであると仮定する
つまり, (x,y) の位置から入射する光線は, xy 平面上の同じ位置から出ますが, わずかに異なる方向へ進みます. これが焦点に与える影響について考えてみましょう. 下の画像に見られるように, 屈折率の変化は光線をわずかに乱すので, わずかに多い (またはわずかに少ない) 光がナイフエッジによって遮られます. これは, 画像平面上の明暗として現れ, 基本的な動作原理となります.
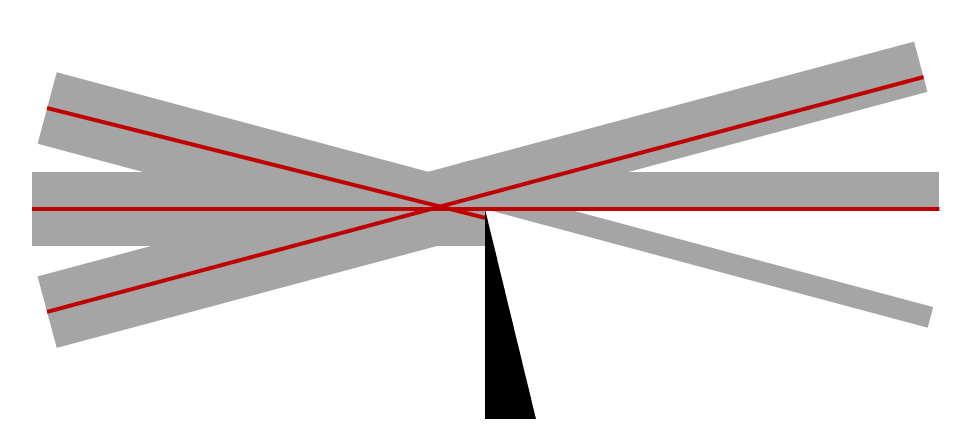
焦点での摂動光線. ナイフエッジは, わずかに異なる角度で入射した光線に対して, 異なる量の光を遮断します.
ナイフエッジは x 軸や y 軸に平行になるように回転させたり, ピンホールビームストップに置き換えることができ, それぞれ異なる明暗のパターンを生成します. シュリーレンイメージングにおけるこれらの明暗の帯は, 流れドメインを通る以下の積分に相関しています.
| 障害物タイプ | 式 |
|---|---|
| ナイフエッジが x 軸に平行 | \int \frac{\partial n}{\partial y} \partial z |
| ナイフエッジが y 軸に平行 | \int \frac{\partial n}{\partial x} \partial z |
| ピンホール閉塞 | \int \sqrt{\frac{\partial n}{\partial x}^2 +\frac{\partial n}{\partial y}^2} \partial z |
実は, これらの積分は COMSOL Multiphysics を使って簡単に実装できます.
COMSOL® ソフトウェア内での実装
画像を作成する前に, 計算流体力学の側面の1つである圧縮性流体の扱いについて触れておく必要があります. つまり, 数値モデリングの都合上, 流体の密度は一定であることを仮定することが多いのです. これは流れモデルの観点からは全く妥当なことです. 密度の変動が1 % 以下であれば, 速度場や圧力場の解はあまり変化しませんが, 屈折率はかなり大きく変化します. したがって, ブシネスク近似などで密度が一定であると仮定して流れをモデル化している場合は, 圧力場 (計算されている場合は温度場) を使って, 空間的な密度変化を事後評価するようにしてください. 大気中の空気の場合, 理想気体の法則を用いるのが適切ですが, ゲージ圧ではなく, 絶対圧で行うようにしてください.
モデリング空間内の密度変化の式ができたら, それを使って屈折率分布と, 屈折率の1方向または2方向の導関数を計算することができます. これには, 組み込みの微分演算子を使用します. 例えば, 密度を表す式が変数 rho であれば, x 方向の微分を d(rho,x) とすることができます. あとは, この式の積分を流れに沿った方向にとり, 流れに平行な平面上にプロットするだけです. これには, 一般射影演算子を使います. 流れドメイン外の境界に投影することも可能です. これは, 流れドメインの境界上に存在するメッシュよりも細かいメッシュでこの演算子を評価したい場合に, 非常に有利になります.
また, 流れの中に不透明な障害物がある場合のことも考える必要があります. このような場合, 上記の積分をあらゆる場所で評価することは望ましくありません. COMSOL Multiphysics バージョン6.0以降の CAD インポートモジュール, デザインモジュール, または LiveLink™ 製品で利用できる作業平面投影機能を使用して, 障害物の輪郭を光学出射面境界に投影し, 影がない表面上の積分のみを評価します.
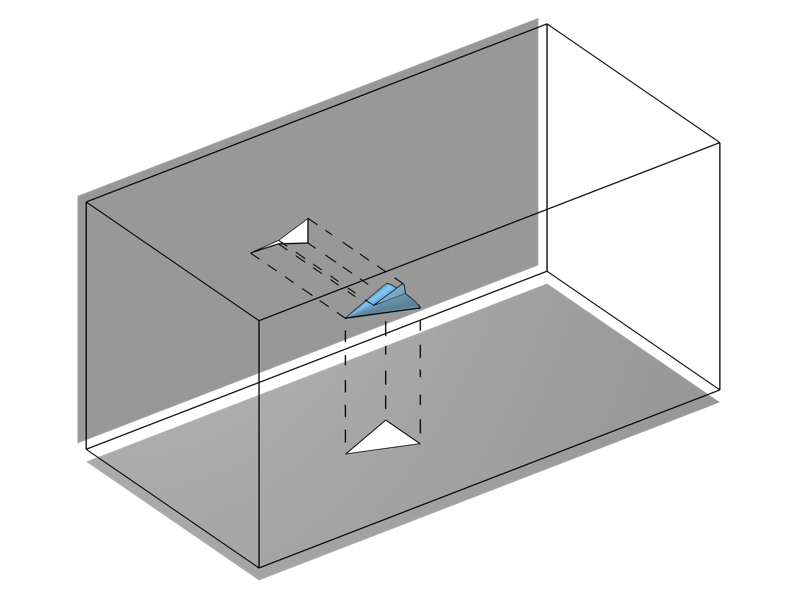
ジオメトリの輪郭を平面に投影するワークプレーン射影機能.
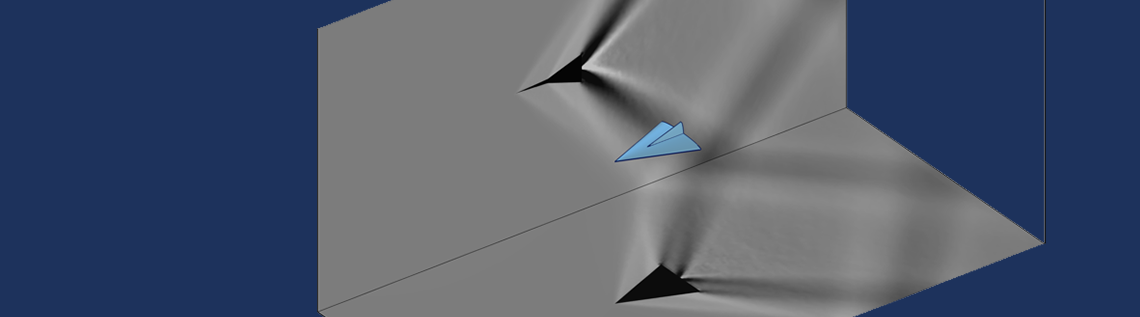
これらのモデリング技術を駆使すれば, シュリーレンイメージングの実験結果と相関のあるプロットを作成することができます. 下の画像は, オイラーバンプのチュートリアルモデルで示したような, 物体周辺の高マッハ数の流れを示したものです. この同じ手法は, 音響モデルの結果を可視化するためにも使用できます.
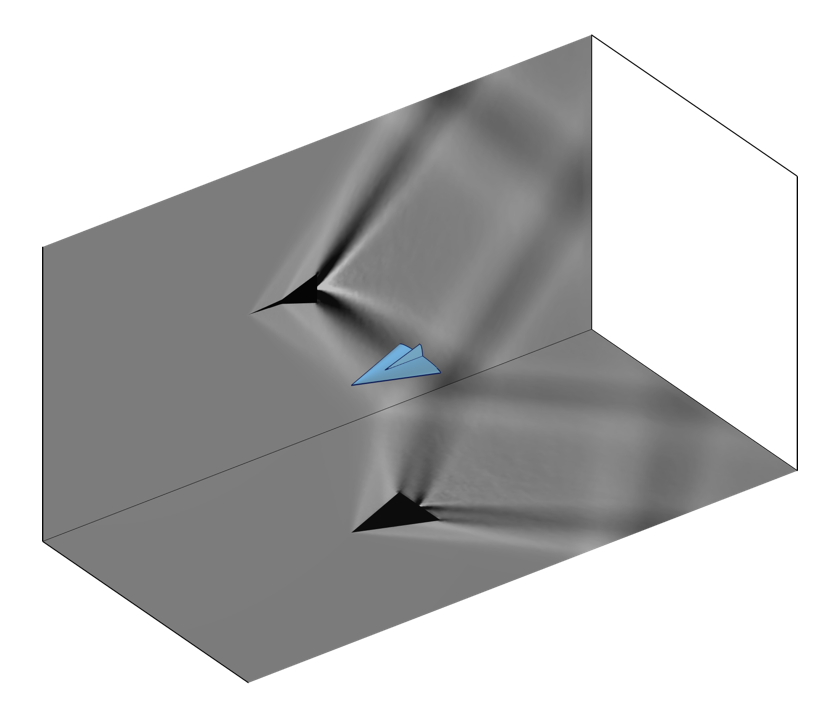
一般射影演算子によって作成された, 遷音速風洞内のモデルのシュリーレンイメージングに相関する画像.
次のステップ
ソフトウェアの CFD モデリング機能についてもっと知りたい方は, 是非お問い合わせください!


コメント (0)