
AC/DC モジュールを使用して定常状態, 過渡状態, または周波数領域で磁場をモデル化するときは常に, モデルを解くために必要な計算リソースと時間を最小限に抑えるために, モデルのサイズをできるだけ小さくする必要があります. 今日は, モデリングで利用できる対称境界条件を紹介し, その使用方法を示します.
3つの対称面を持つコイルのモデル化
まず, 下の図に示すように, 長方形に巻かれたマルチターンコイルを見てみましょう. 球状のモデリング領域には長方形のコイルが含まれています. コイル領域は, 長方形のプロファイルの周りに巻かれた数百ターンのワイヤーを表します. コイルを励起するリード線はモデルから無視され, コイルは電流の閉ループとして扱われます. マルチターンコイル 機能は, コイルのプロファイルの周りに均一な電流分布を計算して適用するために使用され, 定常状態の磁場がプロットされます. コイル領域の断面積は, 電流の経路をたどると一定になることに注意してください.
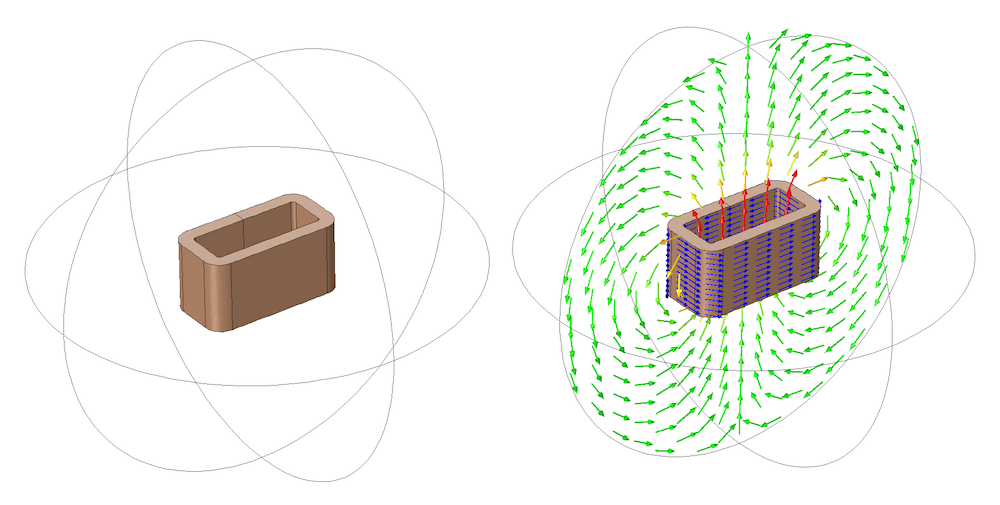
巻き方向に沿って電流が流れる長方形のコイル. 電流の流れ (青い矢印) と磁場がプロットされています.
このモデリング領域には, 3つの対称面, つまりジオメトリが正確にミラーリングされる平面があります. 次に, この幾何学的対称性と磁場および電流が流れる方向に関する知識を使用して, モデリング領域のサイズを縮小する方法を見てみましょう.
磁気絶縁 境界条件
磁気絶縁 境界条件は, 磁場の鏡面対称面を表します. 磁場は, 面を横切ると正確に鏡像になります.
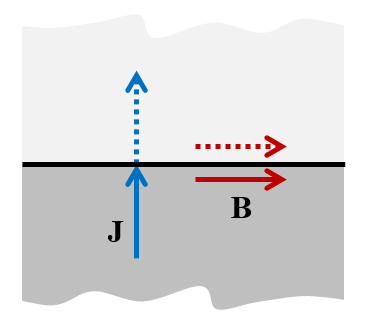
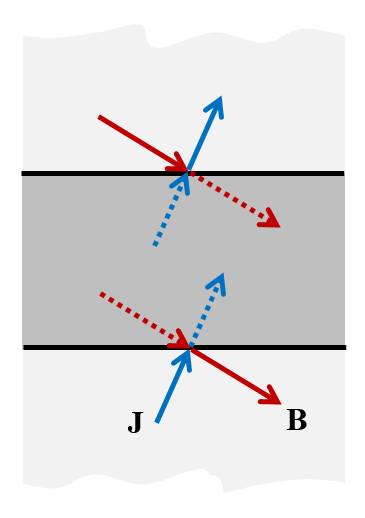
磁気絶縁 境界条件 — “J に垂直に, B に平行にカット”.
この境界条件は, 境界の法線方向の磁場がゼロであることも意味します. つまり, 磁場はこの境界に対して接線方向でなければなりません. 結果として, この境界条件は, 電流が 法線 方向にのみ流れる境界という物理的な解釈を持ちます. モデリングルールは次のように要約できます: “磁気絶縁 を使用して, J に垂直に, B に平行にカットします.”
完全磁気導体 境界条件
一方, 完全磁気導体 境界条件は, 電流の鏡面対称面を表します. 数学的な観点からは, 磁気絶縁 境界条件の “反対” と考えることができます.
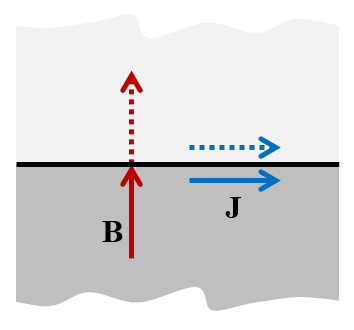
完全磁気導体 の境界条件 — “B に垂直に, J に平行にカット”.
電流ベクトルは平面を横切るときに正確に鏡像になり, 法線成分を持つことはできないため, 電流は 接線方向に流れる必要があります. この境界条件は, 境界に近づくときに磁場が接線成分を持たないようにするため, 磁場は法線方向のみを指し, 境界を横切っても符号を変えることはできません. モデリングルールは次のようにまとめることができます: “完全磁気導体 を使用して, Bに垂直に, J に平行にカット.”
簡略化されたコイルモデル
元のジオメトリは, 元のジオメトリを表す 1/8 モデルにサイズを縮小できます. 以下に示すように, コイルの中心を通る直交平面を使用してドメインを分割します.
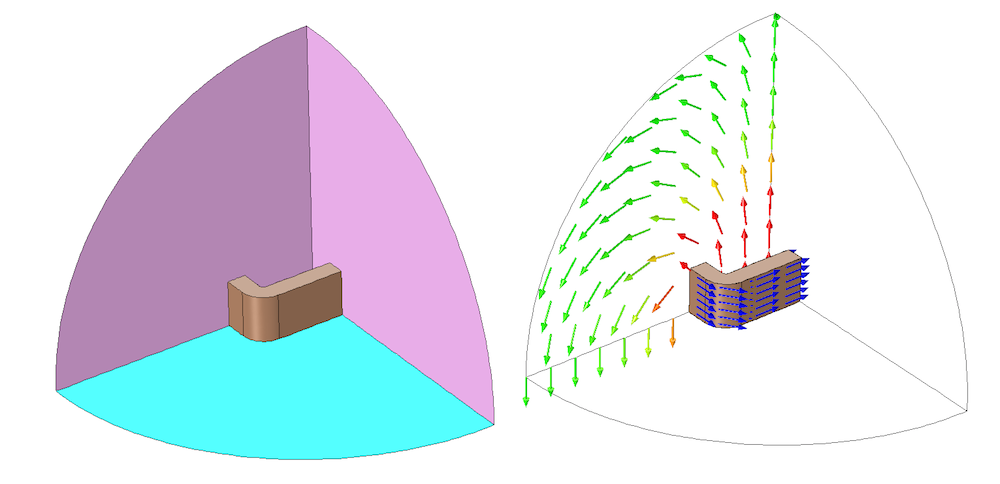
巻き方向の周囲に電流が流れる長方形コイルの 1/8 対称モデル. この問題の適切な対称面に沿って, 磁気絶縁 (マゼンタ) と 完全磁気導体 (シアン) の境界条件が適用されます.
磁気絶縁 境界条件は, 電流が通常に流れる平面を表す2つの境界に適用されます. コイルが電圧境界条件で励起される場合, 適用される 磁気絶縁 対称条件ごとに電圧を2分の1に減らすことが重要です. コイルが電流で励起される場合, 適用される電流を変更する必要はありませんが, ポスト処理されたコイル電圧は, 磁気絶縁 対称条件ごとに2分の1にスケーリングする必要があります.
完全磁気導体 条件は, 電流が接線方向に流れる平面で使用されます. 完全磁気導体 条件はコイルを半分に切断するため, 電流励起を使用する場合は適用される電流を半分に分割することが重要です. 一方, 電圧励起を使用する場合, ポスト処理されたコイル電流は, 各 完全磁気導体 対称面ごとに2倍に拡大する必要があります.
周期的 (境界) 条件
ほとんどの場合, 磁気絶縁 および 完全磁気導体 境界条件は, モデルのサイズを大幅に縮小するのに十分です. 前に説明したように, これらの条件は, 電流と磁場が境界に対して垂直または接線になるように強制します. しかし, 幾何学的対称面があり, 磁場がそのような対称性を持たない場合はどうなるでしょうか. そのような場合は, 周期的 (境界) 条件が適切である可能性があります.
周期 条件は, 解が周期的であることがわかっている場合に使用されます.
周期 (境界) 条件は, 電流と磁場ベクトルの両方が境界に対して角度をなすことができる, より一般的な対称性を可能にします. この条件の使用は, 磁気源と構造が空間内で周期的である場合に限定されます. 通常, 完全なジオメトリは, 周期条件によって制限される最小の繰り返し要素, つまり単位セルに縮小できます.
以下に示す, 1本のワイヤーで巻かれたトロイダルインダクターの構造を考えてみましょう. リード線による非対称性を無視すれば, ワイヤーはトロイドの周囲を1本の連続した螺旋としてかなり正確にモデル化できる. ワイヤーをエッジ電流としてモデル化し, ワイヤーの接線方向に流れるようにすることができます.
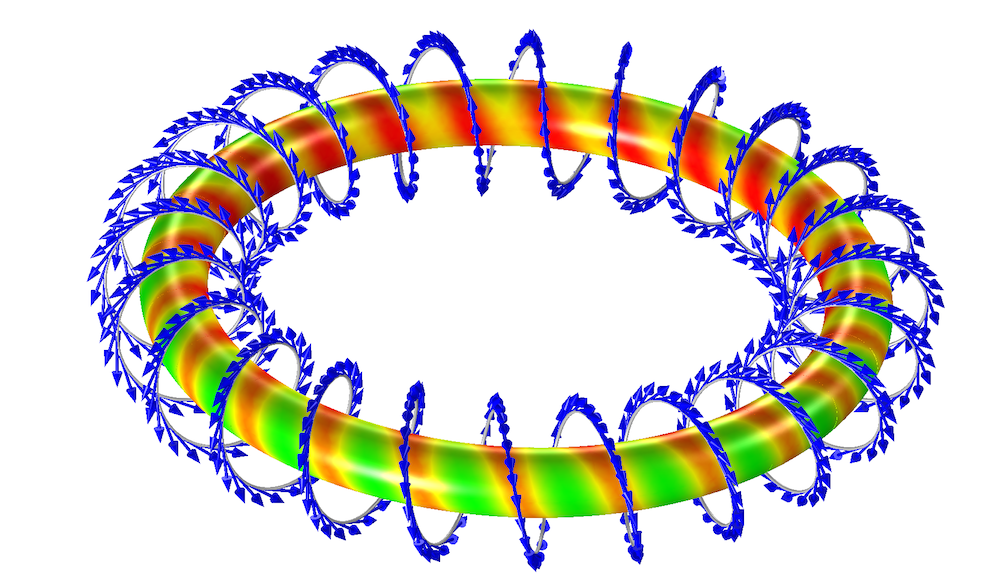
螺旋状に巻かれたトロイダルインダクター. 矢印 (青) は電流の方向を示します. コア内の磁場が表示されます.
ここでできるだけ対称性を活用するために, 巻き線の1ターンを含む元のモデルの小さなスライスである単位セルを検討できます. スライスの側面には 周期 条件が使用されます. この境界条件を使用する場合, メッシュは周期面上で同一である必要があります. そのため, メッシュが同一になるように フェースコピー 機能を使用する必要があります. 下の画像からわかるように, モデルのサイズは巻線の数だけ縮小でき, 問題のサイズを大幅に縮小できます.
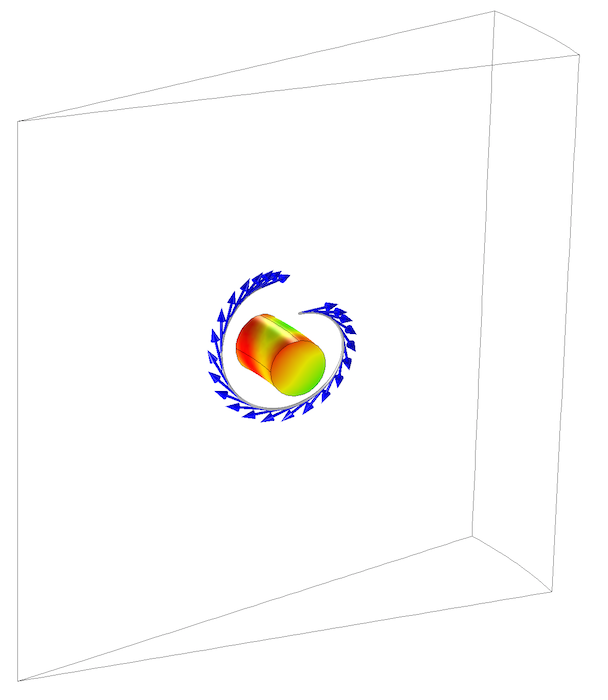
周期条件は, 特定のジオメトリのモデルのサイズを大幅に縮小できます.
周期 条件の汎用性は, より基本的な 磁気絶縁 条件や 完全磁気導体 条件と比較して, コストがかかります. ジオメトリの片側の未知の場を反対側の未知の場にリンクするため, 剛性行列がより高密度になり, 求解にコストがかかります. したがって, より基本的な条件が適用される場合は使用しないでください.
対称面 境界条件
バージョン 6.0 では, 新しい 対称面 境界条件 (下図参照) が導入されました. この機能は, 磁束密度に 対称 条件 (前述の 磁気絶縁 境界条件と同等) または 反対称 条件 (完全磁気導体 境界条件と同等) を適用します. この新しい機能は, 代わりにモデル設定を簡素化するために使用できます.
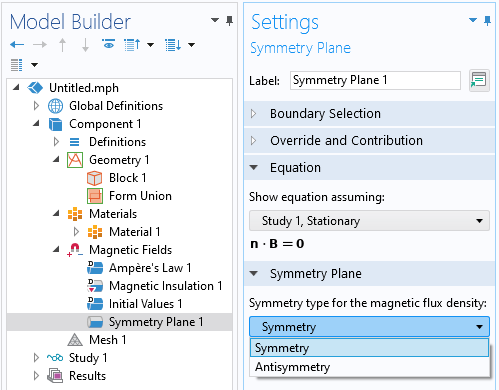
新しい 対称面 境界条件のスクリーンショット.
磁場をモデル化する際に対称性を活用することのまとめ
モデルのサイズを小さくすることで, 計算要件も大幅に削減されます. 実際, 計算要件は問題のサイズとともに指数関数的に増加するため, 使用できる対称性が多いほど良いです. 求解したい問題全体に対称性がない場合でも, モデル化の初期開発段階では, 対称性を持つ小さなモデルで作業することが推奨されることがよくあります.
次のステップ
対称境界条件についてさらに詳しく知りたいですか? 下のボタンからお問い合わせください:
その他のリソース
- シミュレーションスキルを練習したい場合は, 次の関連チュートリアルモデルをご覧ください:
編集者注: このブログは, COMSOL Multiphysics® ソフトウェアバージョン 6.0 で利用可能な新機能についての説明を含めるため, 2022年8月31日に更新されました.






コメント (0)