COMSOL Multiphysics® ソフトウェアのアドオンである AC/DC モジュールの一般的な用途の一つは, 時間変動磁場中で大きな誘導電流が発生する導体やその他の損失材料をモデル化することです. 適切なモデリング手法は, 磁場が時間とともにどれだけ速く変化するかによって異なります. ここでは, 基本事項を確認し, 使用する様々なモデリング手法について説明します.
AC/DC モジュールを用いた表皮効果の記述
導体などの損失材料が時間変動電磁場に曝露されると, その材料内に電流が誘導されます. これらの電流は磁場を発生させ, 材料内の電流分布を変化させます. その結果, 誘導電流は損失材料の表面を優先的に流れます. これは 表皮効果 として知られています.
この効果は, AC/DC モジュール と, 次のような磁場と電流を解析するフィジックスインターフェースのいずれかを使用してモデル化できます:
- 磁場 インターフェース
- 電磁場 インターフェース
- 磁場定式化 インターフェース
- 磁場 (回転機械) インターフェース
これらのフィジックスインターフェースはすべて, 磁場 およびその他のすべての場が時間とともに正弦波状に変化するという仮定の下, 周波数領域でのモデリングをサポートしています. 磁場 インターフェース, 磁場 (回転機械) インターフェース, および 磁場定式化 インターフェースは, 完全な時間領域解析をサポートしており, 場は時間とともに非正弦波状に変化します.
時間変動磁場における導体の周波数領域シミュレーション
まず, 周波数領域に焦点を当てます. これは非常に合理的な手法です. なぜなら, ほとんどの電気機器は既知の周波数または周波数範囲で動作するためです. 動作周波数に基づいて, 材料の表皮厚さ δ を計算できます:
ここで, \omega は動作周波数, \mu_0 は透磁率, \epsilon_0 は自由空間の誘電率, \mu_r および \epsilon_r は材料の比透磁率と誘電率, \sigma は材料の電気伝導率です.
導体の場合, この式は次のように簡略化できます:
厳密に言えば, 表皮深さは平面半無限導体内の誘導電流の指数関数的減少によって定義されますが, 形状に関わらず有用な指標です. まず, シミュレーションで使用するすべての材料の表皮深さを常に推定します. この値によって材料のモデル化方法が決まるためです. この重要な点を理解するために, 以下の模式図に示すように, 異なる周波数で均一な背景磁場に曝露された閉ループ状の電線 (電線半径 1 cm, ループ半径 10 cm) の単純な例を見てみましょう.
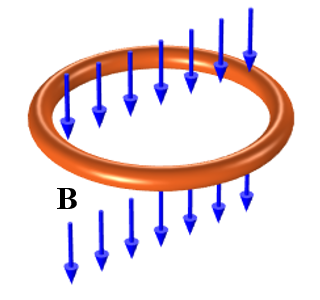
正弦波状に時間変化する磁場に曝露された銅線ループ.
上に示した問題は, 以下に示すように, 2次元軸対称モデルを用いてモデル化できます. 前回のブログ で説明した理由により, モデリング空間を切り捨てるために無限要素領域が使用されます.
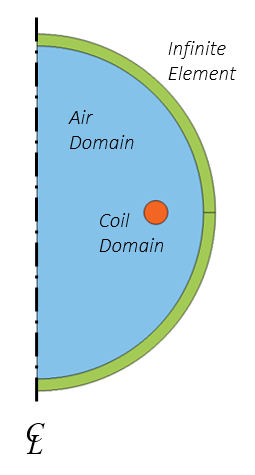
コイルモデルの概略図.
様々な周波数における結果を見てみましょう. 下の図は, コイルに流れる電流の大きさを示しています. 高周波数では, 電流が主にコイルの表面付近を流れる様子が分かります. 実際, 最高周波数では, コイル中心部の電流は実質的にゼロです. つまり, 表皮効果によって導体内部がシールドされているということです.
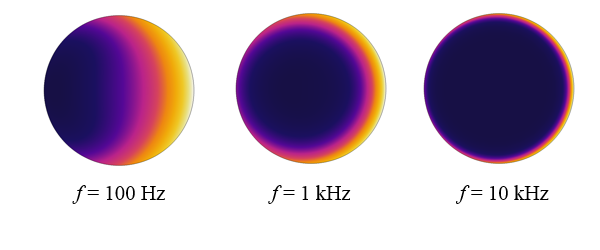
様々な周波数におけるコイル断面内の電流の流れ.
これらの様々なケースを適切にモデル化するには, 使用する有限要素メッシュにも注意する必要があります. 高周波数では, 電流が境界に近づくにつれて, 場の空間変化を解析するために, より細かいメッシュが必要になります. しかし, 場は境界に垂直な方向にのみ大きく変化し, コイルの周囲に沿っては非常に緩やかに変化します.
このような場合, 境界層メッシュ機能を使用するのが適切です. この機能は, 下図に示すように, 境界に垂直な薄い要素を挿入します. コイル内の電流分布をどの程度正確に解析したいかに応じて, 境界層要素の厚さを表皮厚さの半分から1つまで調整し, 使用する境界層要素の数は2から8以上まで選択できます. 一方, 周波数が十分に低い場合は, 境界層メッシュはまったく必要ありません.
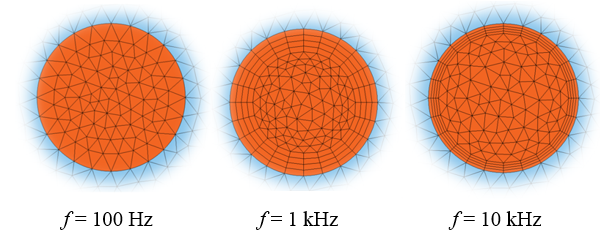
電流分布の以前のプロットに対応する, さまざまな周波数におけるワイヤー内のメッシュ.
等価境界条件
上の図から, 高周波数では電流分布がコイル内部にほとんど及ばないことも分かります. したがって, 実用上は, 十分に高い周波数では電流は表面を流れると言えます. このような場合, 下の図に示すように, インピーダンス 境界条件を使用し, コイル 内部 を全くモデル化せずに済みます.
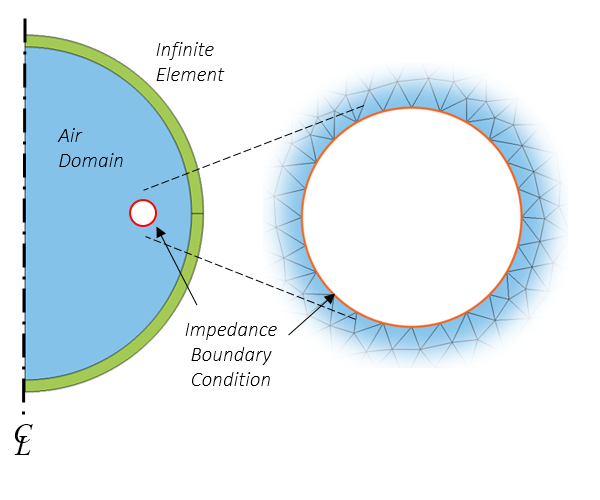
インピーダンス 境界条件を用いたモデルの概略図とメッシュ.
このアプローチにより, 空気領域をメッシュ化し, インピーダンス 境界条件を適用するだけで済むため, 計算量が大幅に削減されます. もちろん, 導体内の電流分布といった情報は失われますが, それを気にしないのであれば, このアプローチは導体内部をメッシュ化するよりも優れた代替手段となり得ます. 下の最初のグラフは, インピーダンス 境界条件と境界層メッシュを用いたコイルの領域モデルを用いて計算された, コイルの損失と周波数の関係を示しています.
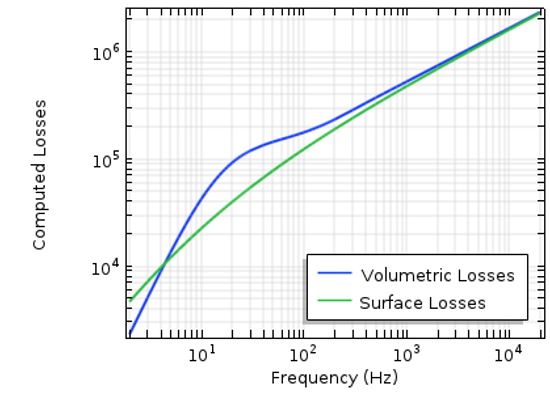
領域モデルと インピーダンス 境界条件を用いて計算された損失のグラフ.
次の図は, インピーダンス 境界条件を用いて計算された損失と, 領域を明示的にモデル化して計算された損失の比をプロットしたものです. この比は, ワイヤー半径と表皮深さの比に対してプロットされています. 部品の特性寸法 (この場合は半径) が表皮深さの10倍に近づくにつれて, これら2つのアプローチで計算された損失は類似したものになります.
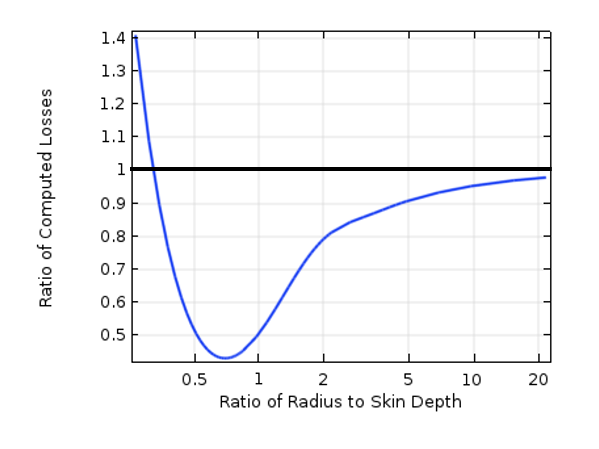
計算された損失の比と, 物体サイズと表皮深さの比の関係を示すグラフ.
上のグラフから, 表皮深さがモデル化対象の導体の寸法に比べて比較的小さい限り, インピーダンス 境界条件によって総損失を正確に予測できることがわかります. これは重要な結果であり, AC/DC モジュールにおける周波数領域モデリングの多くを大幅に簡素化できます.
時間変動磁場中の導体の時間領域シミュレーション
最後に, 時間領域シミュレーションについて触れてこのトピックを締めくくりましょう. インピーダンス 境界条件は, この境界条件がマックスウェル方程式の周波数領域形式に基づいて定式化されているため, このケースでは利用できません. 時間領域シミュレーションでは, すべての導体の内部をモデル化し, メッシュ分割する必要があります. 境界層メッシュ分割は依然として適切ですが, 時間領域励起の平均および最大の予想される周波数成分に基づいて要素の厚さを調整する必要があります. もちろん, これはモデルの計算コストを大幅に増加させる可能性があるため, 可能な限り周波数領域でモデル化するようにしてください.
では, 磁場強度に対して非線形な材料や, 時間領域でモデル化する必要があると思われる材料がある場合はどうすればよいでしょうか? その場合, どうすればよいでしょうか? 非線形透磁率を持つ強磁性材料を想定している場合でも, 有効 H-B 曲線機能を使用して 周波数領域で磁性材料をモデル化 できます.
まとめ
AC/DC モジュールを効果的に使用するには, 時間変動磁場と相互作用する導電性で損失のある材料のモデル化方法を十分に理解することが重要です. 導体領域を明示的にモデル化するか, 高周波数において インピーダンス 境界条件を使用して導体をモデル化することができます. 導体領域を明示的にモデル化する場合は, 高周波数における電流の解像度を高めるために境界層メッシュを使用する必要があり, 計算要件が増加します. インピーダンス 境界条件を使用すると近似値が導入されますが, 導体領域の内部をモデル化する必要がないため, 計算リソースを大幅に節約できます.
次のステップ
AC/DC モジュールで利用可能な電磁気モデリングの特殊な機能について詳しくは, 下のボタンをクリックしてください.
その他の資料
このトピックに関する補足演習に取り組むには, 以下のチュートリアルをご覧ください:






コメント (0)