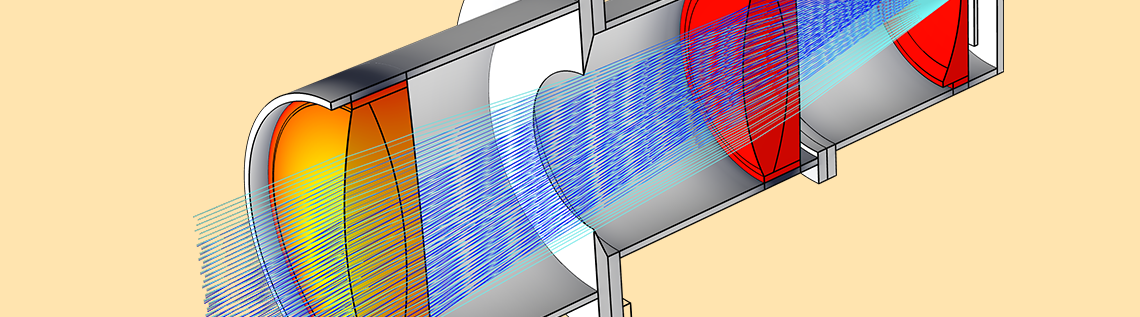
現代の光学システムは, 高高度, 宇宙, 水中, レーザーおよび原子力施設などの過酷な環境で動作を求められることが多くあります. このような光学系は, 構造的負荷と極端な温度にさらされます. このような環境の影響を完全に把握するには, STOP (Structure-Thermal-Optical Performance) 解析による数値シミュレーションが最も正確です. STOP 解析は, 典型的なマルチフィジックス問題です. このブログでは, COMSOL Multiphysics® ソフトウェアを使用して, 構造, 熱, および光学効果を組み合わせる方法を紹介します.
モデルの説明:ペッツバールレンズ系の例
この例では, 熱真空チャンバー内のペッツバールレンズ系を検討します. 真空チャンバーの壁は非常に低い温度に維持され (おそらく宇宙空間の影響を模倣するため), レンズ系ははるかに高い温度で隣接する部屋を調べます (おそらく実験室でのテストをエミュレートします). モデルジオメトリの分解図を以下に示します.
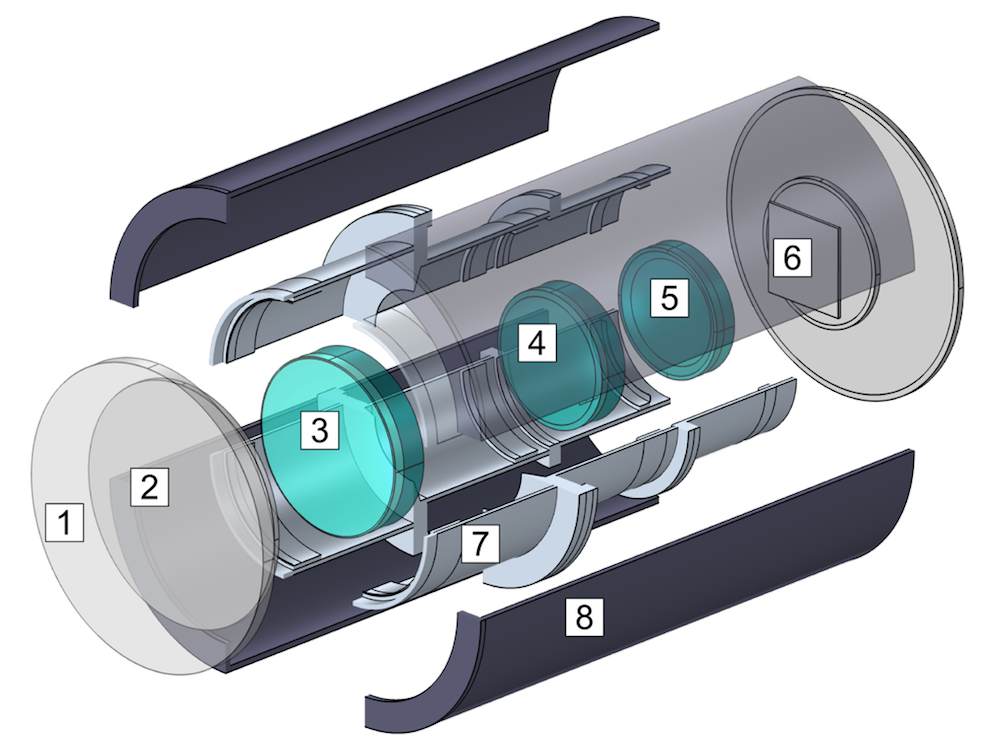
入射光は, ペッツバールレンズ系に到達する前に, 最も外側の真空チャンバー窓 (1) から系に入り, 次にチャンバー内の追加のサーマルウィンドウ (2) から入ります. レンズ系自体は, 2つのレンズグループ (3と4) とフィールドフラットレンズ (5) で構成されています. 光は焦点面 (6) に焦点を合わせます. レンズ系は, サーマルシュラウド (8) 内に完全に囲まれたバレル (7) によって支持されています.
外側の真空窓の反対側の周囲環境は穏やかな25°Cですが, サーマルシュラウドの壁は過酷な-50°Cに維持されています. この固定温度は, たとえば, シュラウドに冷たい液体を流すことによって維持できますが, このメカニズムについては詳しく説明せず, 単に壁を固定温度境界条件として扱います. 暖かい周囲環境から入ってくる熱輻射は, レンズ系とバレルに温度勾配を作ります. 直感的には, 真空ウィンドウはレンズグループ1よりも暖かいサーマルウィンドウよりもさらに暖かいと予想されるかもしれませんが, より定量的な情報が必要です.
このモデルの設定について詳しく説明する前に, 熱真空チャンバー内で機能しているさまざまな物理現象について考えてみましょう.
STOP 解析の基本的なフィジックス
STOP モデルには, 以下の間のカップリングが含まれます.
- 伝熱 (固体)インターフェースまたは他の伝熱インターフェースを使用した温度計算
- 固体力学インターフェースまたはもう一つの構造フィジックスインターフェースを使用した構造変形モデリング
- 幾何光学インターフェースを使用した光線追跡
これらの3つのフィジックスの分野をカップリングするメカニズムは, 以下のフローチャートに要約されています.
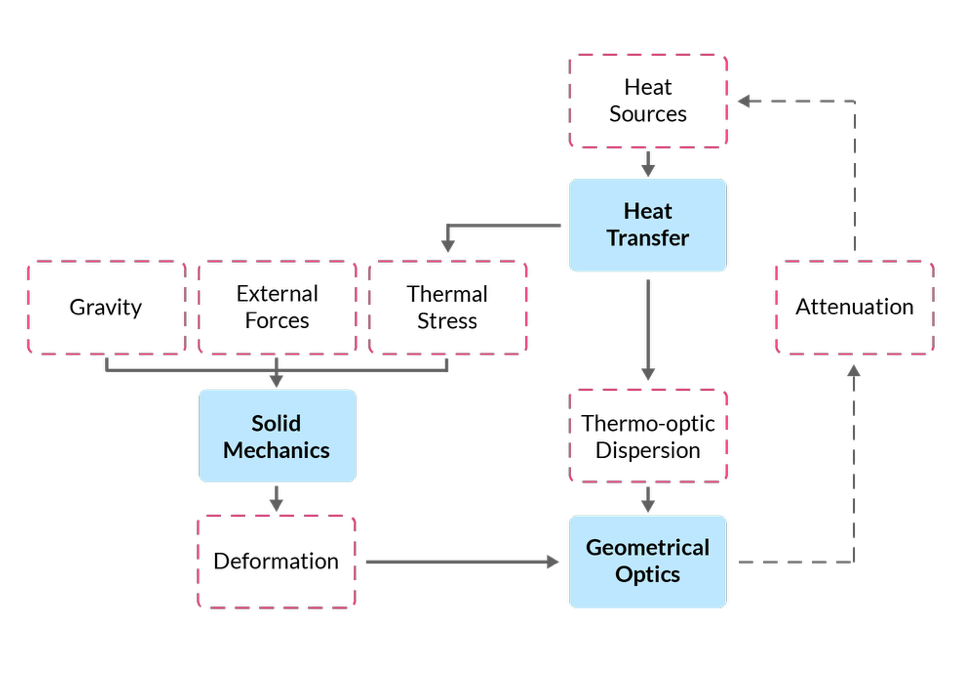
STOP 解析における最も重要なマルチフィジックス現象のフローチャート.
熱モデリング
温度は,ジュール熱や化学反応などの熱源とシンク, および周囲との対流または輻射熱交換などの境界条件の影響を受けます.
特別なケースは, 光線光学と熱伝達の間の双方向 (双方向) カップリングです. これは, 強力なソース (たとえば, レーザーまたはソーラー集光器から) がモデリングドメインで減衰を受け, 追加の熱源が生成される場合に発生します. このブログで説明されている例は一方向です. 光線は, 減衰によって重要な熱源項を生成するほど強力ではありません.
温度は, 屈折率が温度の関数である熱光学分散を介した光線の伝播に影響を与えます .次のセクションで説明するように, 熱応力が境界の変形を引き起こす可能性があるため, 温度も間接的に光線経路に影響を与えます.
構造モデリング
通常, STOP 解析では, 構造物の変位場を計算する必要があります. 変形したジオメトリに光線が入射すると, 元の変形していないジオメトリとは異なる方向に光線が反射したり屈折したりすることがあります.
構造的な変位は, モデルの形状に加わるすべての力の結果であり, この場合, レンズ系とそれを固定する鏡筒で構成されています. また, 温度変化によって膨張または収縮するため, 熱応力によっても形状が変形することがあります.
光分散モデル
境界を越えて反射屈折する光線を追跡するために, 幾何光学インターフェースが使用されています. 各材料の屈折率は, 波長と温度の両方の関数となります. レンズ系が変形している場合, 光線は変形したジオメトリと相互作用します. このように, 光線の経路は, 熱的現象と構造的現象の両方から影響を受けます.
幾何光学インターフェースの材料特性ノードを使用して, 光分散モデルを選択することができます. 光分散モデルとは, 真空の波長 (場合によっては温度) の関数として屈折率を定義する方程式と係数のセットです.
次のスクリーンショットは, セルマイヤー光分散モデルの方程式表示です. 最初の5行の式は, 真空の波長の関数としての屈折率を定義しています. ここで, A1, B1, A2, B2, A3, B3はセルマイヤー係数で, ガラスの種類ごとに固有のものです. 最後の2行は, 熱光学分散モデルの追加補正項です. ここで, D0, D1, D2, E0, E1, λTKは, 熱光学分散係数です.
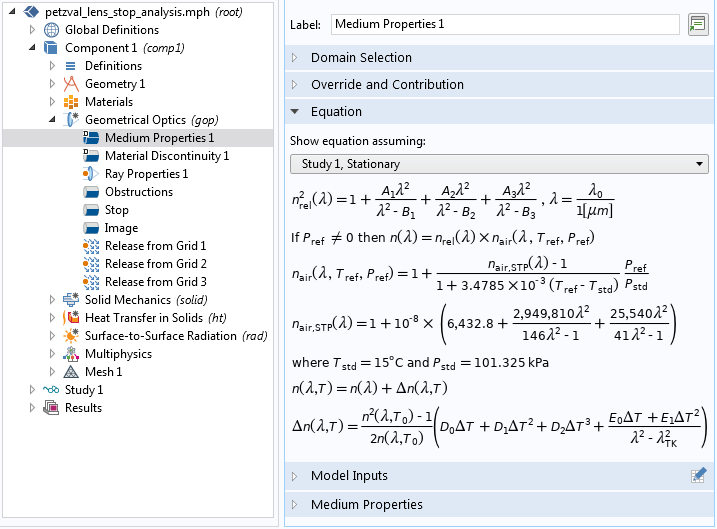
セルマイヤー光分散モデルの方程式.
ここで1つの特別な選択肢を指摘しておきましょう. 温度依存のセルマイヤー分散モデルは,温度と波長の依存を1つの方程式に結合します. このオプションは, ガラスが非常に広範囲の温度にさらされる極低温モデルとして最もよく使用されます.
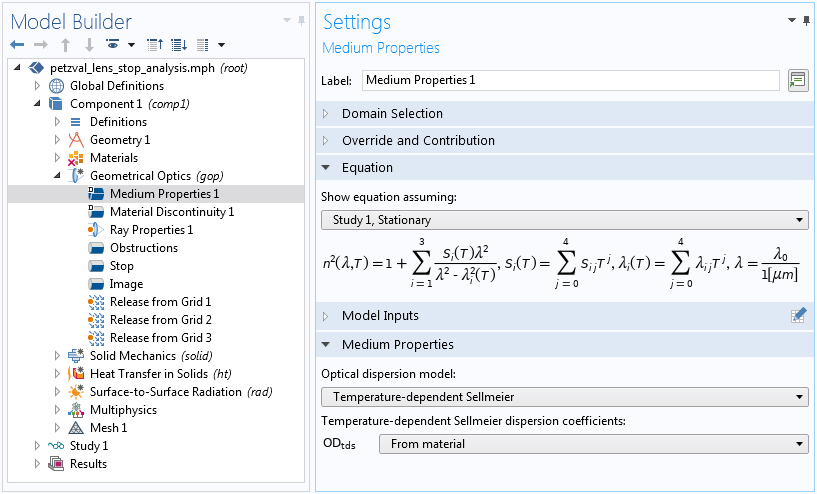
温度依存のセルマイヤー係数で, 温度依存と波長依存を一つの式にまとめたもの.
通常,光学分散モデルのリストから材料から分散モデルを取得を選択することをお勧めします. すると, 各材料にどのような材料特性が定義されているかに基づいて, 光分散モデルが自動的に検出されます.このオプションを使用すると, 異なるメーカーの複数のガラスで, 光分散モデルに異なる規約を使用している場合でも, モデルを作成することができます.
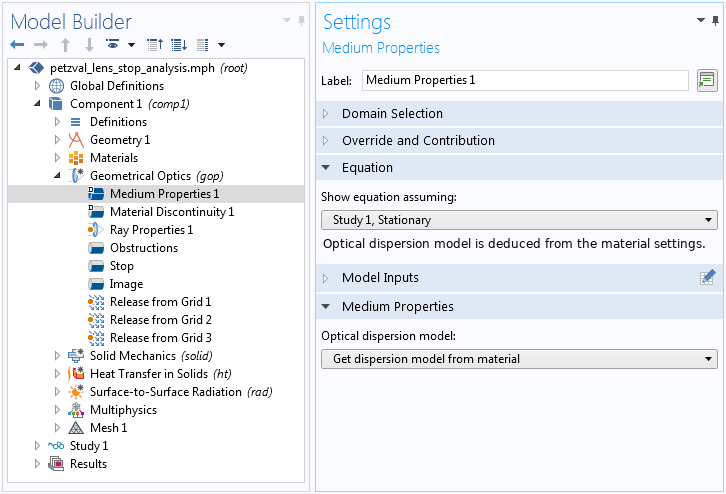
定義されている材料特性に基づいて, 正しい光分散モデルを自動的に検出するオプション.
ペッツバールレンズ系の再考
次に, 前述のように, 熱真空チャンバー内のペッツバールレンズ系の STOP 解析の例を考えてみましょう.
熱伝達は, 熱伝導用の伝熱 (固体)インターフェースと, 表面対表面または表面対周囲環境の輻射輸送用の表面‐表面輻射インターフェースを使用してモデル化されます. 真空窓の外面のみが暖かい周囲環境にさらされます. 熱伝達と輻射熱伝達を相互に結合するために, 以下に示すように, 表面‐表面輻射マルチフィジックスカップリングノードを備えた専用の熱伝達が利用可能です.
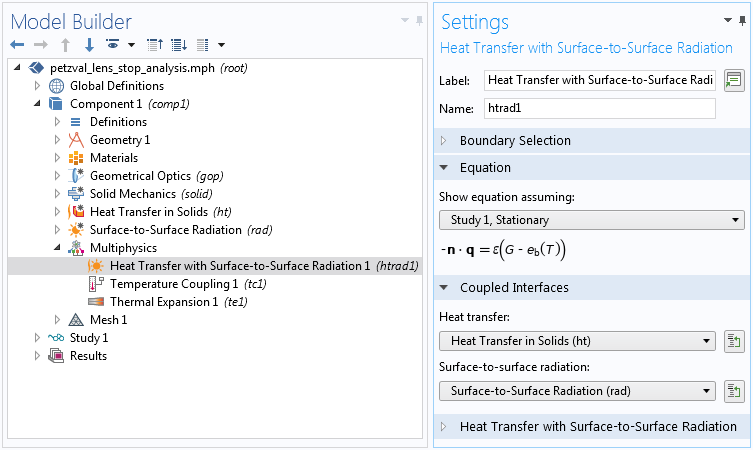
伝熱 (固体)と表面‐表面輻射インターフェースの間のマルチフィジックスカップリング.
表面‐表面輻射インターフェースは, レンズを含むすべての表面で拡散表面境界条件を使用します. したがって, レンズ系は, 可視光の波長では透明ですが, 赤外線では不透明であると想定されます.
レンズ系とバレル内の温度分布を以下にプロットします. マゼンタの実線は, 真空窓 (1), サーマルウィンドウ (2), レンズグループ (3-4), およびフィールドフラットニングレンズ (5) の中心の温度を示します. 青と赤の破線は, それぞれチャンバー壁の固定温度 (6) とチャンバー外の周囲温度 (7) です.
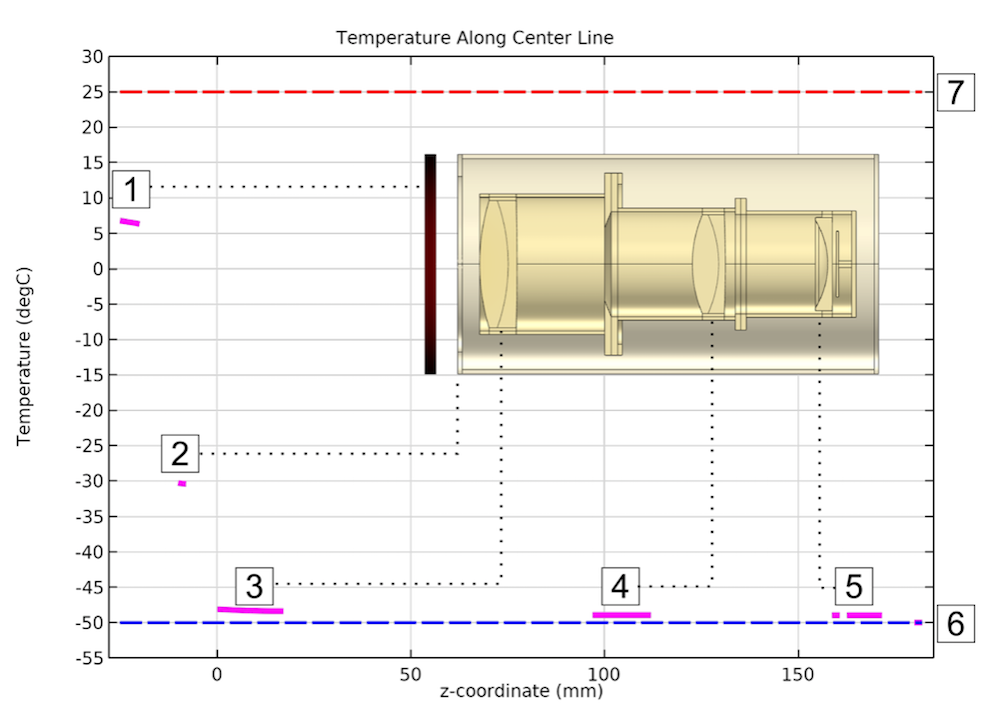
レンズ系, 鏡筒, チャンバーの対称軸に沿った温度のプロット.
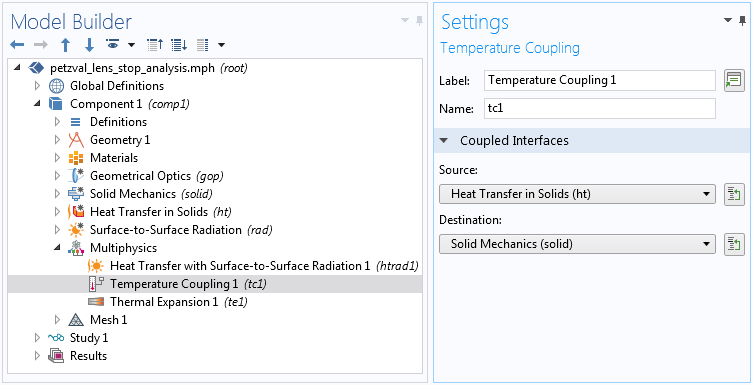
このモデルでは, 構造現象と熱現象のカップリングを2つの専用マルチフィジックスカップリングノードで行っています (下図).このノードの1つは2つのインターフェース間の温度を単純に結合し, もう1つは構造変位の方程式に熱応力項を追加します.
左図: 構造物の変位場を解く際に熱膨張を考慮するためのマルチフィジックスカップリング. 右図伝熱 (固体)と固体力学インターフェース間のマルチフィジックスカップリング.
光線を追跡する際に熱膨張を含めるためには, もう1つ重要なステップがあります. 光線追跡スタディステップを選択し, 幾何学的非線形性を含むチェックボックスが選択されていることを確認します. このチェックボックスが選択されていないと, 光線は変形されていないジオメトリの境界と相互作用し, 温度の影響は屈折率の熱光学分散モデルだけになります.
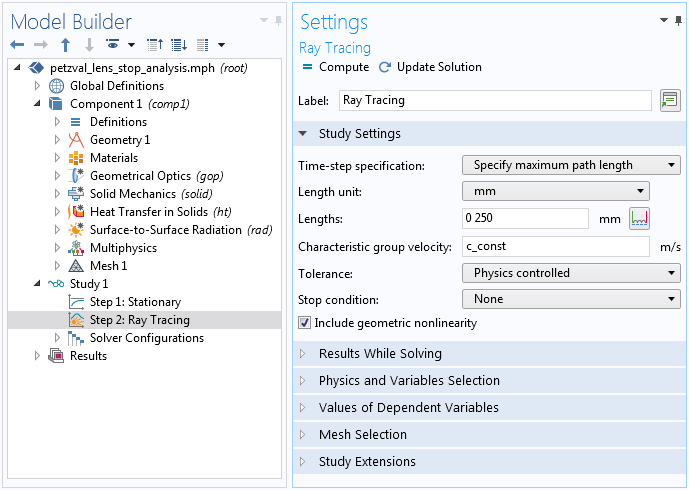
構造的な変形を考慮して, 変形したジオメトリで光線追跡するための設定.
ペッツバールレンズ系の光線図
光線は3つの異なる画角でチャンバー内に出射されます. レンズ系と鏡筒の断面における温度を示す光線図を以下に示します.
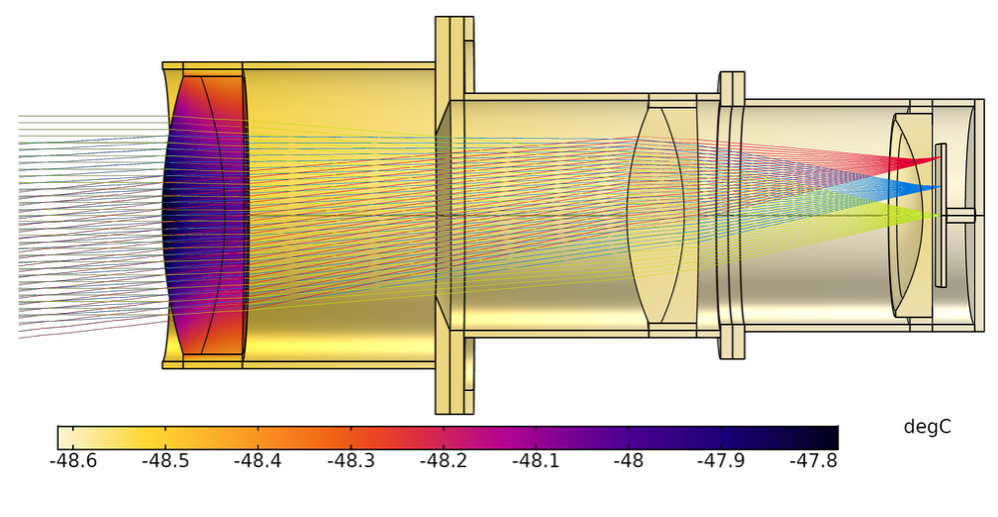
加熱されたペッツバールレンズ系の光線軌道は, 3つの異なる画角に対してプロットしたもの.
焦点面のスポットダイアグラムを以下に示します. 最も対称に見えるスポットダイアグラムはゼロ角に対応し, 最も非対称に見えるスポットダイアグラムは最大画角に対応します.
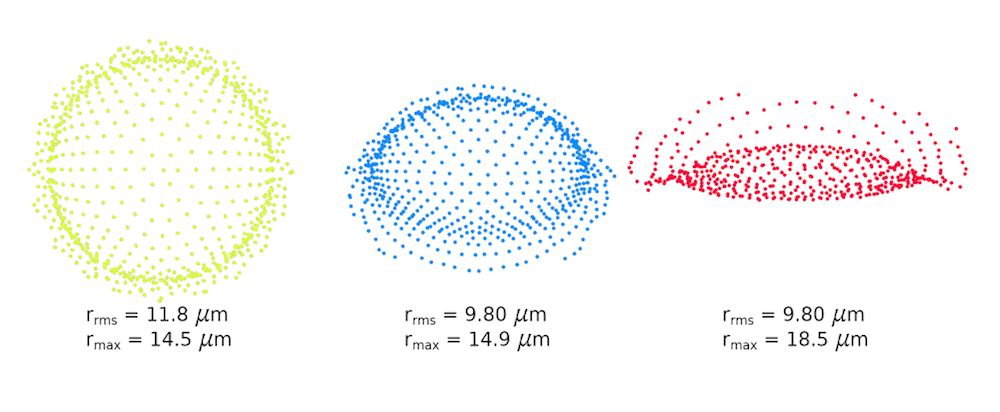
ゼロから始まる3つの画角のスポットダイアグラム (左).
比較のために, 装置全体を室温 (20°C) に保った場合の同じスポットダイアグラムを次に示します.

レンズ系が室温のときの3つの画角のスポットダイアグラム.
COMSOL® ソフトウェアで STOP 解析を行うことについての結論
上記では, 低温の熱真空チャンバーに封入されたペッツバールレンズ系の STOP 解析を行いました. 系が真空チャンバーの外のより暖かい環境にさらされているため, レンズには温度勾配が見られます. 冷たい温度はRMSスポットサイズを著しく増加させます.
以上のように, 構造, 熱, 光学の各現象を一つのモデルにまとめることで, 現実的な試験動作条件で光学系を高精度にシミュレーションするための使いやすいワークフローを提案しました.
以下のボタンをクリックして, 実際にお試しください. このボタンをクリックすると, アプリケーションギャラリーが表示され, チュートリアルドキュメントと, この例の MPH ファイルをダウンロードすることができます.
レンズのモデリングについて詳しく知りたい方は, 複雑なレンズ形状の作成方法に関するブログをご覧ください.


コメント (0)