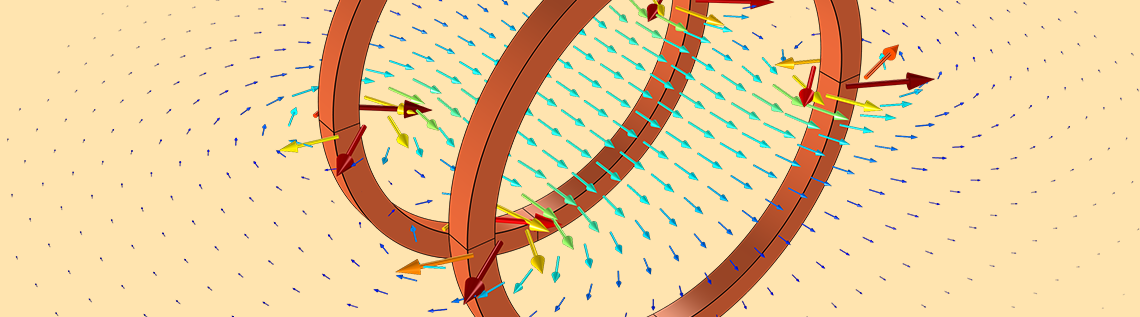
任意のジオメトリ領域内でモデルの結果を表示したいと思ったことはありませんか? モデルにジオメトリを追加して解を再計算する必要があると思われるかもしれません. しかし, COMSOL Multiphysics® ソフトウェアでは, 結果を評価するためだけにパーツを追加して位置を変更するだけで済みます. ここでは, コイル間の相互インダクタンスを計算する例でこれを実証し, よりシンプルな手法を用いて, より限定されたケースセットで使用できる手法について説明します.
相互インダクタンスの計算
以下に示す, 電流を流す2つの円形コイル (それぞれ I0 = 0.25 mA の電流を流す) のモデルを考えてみましょう. 磁束密度 (B 場) は, これらの一次コイルの周囲の空間にプロットされています. ここで, 大きな一次コイルの間に小さなピックアップコイルを配置するとします. このピックアップコイルは磁束の一部を遮断し, その外周曲線 C と囲まれた領域 A によって定義されます.
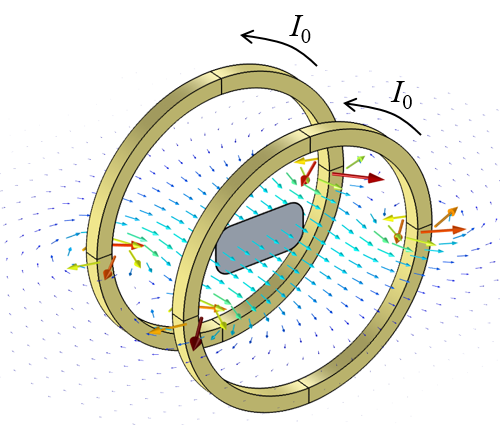
ピックアップコイルを内部に備えたヘルムホルツコイルの周囲の磁束密度. コイルの囲まれた領域は灰色で示されています. ピックアップコイルの向きが変わるにつれて相互インダクタンスを再計算します.
これらの一次コイルとピックアップコイル間の相互インダクタンスは次のように定義されます:
ここで n は表面 A に垂直なベクトルです.
B 場は磁気ベクトルポテンシャルから \mathbf{B=\nabla \times A} と計算されるので, ストークスの定理 を用いると, 上記の面積分は線積分と等しいことがわかります:
ここで t は曲線 C の接線ベクトルです.
相互インダクタンスを計算するこの方法は, アプリケーションギャラリの RFID システム の例にも示されています.
ピックアップコイルを一次コイルの周囲の任意の位置と方向に配置し, モデルを解析して, 上記のいずれかの積分を評価できます. モデルを解析した後, 解更新 機能を使用してピックアップコイルのジオメトリ機能を追加することもできます. この機能は, モデルジオメトリ全体を再メッシュし, 以前のメッシュから計算された解を新しいメッシュにマッピングします. ジオメトリの変更が解に影響を与えず, ピックアップコイルの位置をいくつか試すだけであれば, これは適切かつ簡単に実行できます.
ピックアップコイルのさまざまな位置と方向を試したいとします. A 場は変化しないため, モデル全体を再解析または再メッシュする必要はなく, ピックアップコイルのジオメトリを移動させるだけです. これは, 複数のジオメトリコンポーネント, 一般押出し コンポーネントカップリング, および 積分 コンポーネントカップリングを組み合わせて使用することで実現できます.
COMSOL Multiphysics® における任意のジオメトリの積分実装
既存のヘルムホルツコイルの例を基に, モデルに別の 3D コンポーネントを導入します. この2つ目のコンポーネント内のジオメトリは, ピックアップコイルのエッジ, 断面, および向きを定義するために使用されます. ジオメトリの 回転 と 移動 機能を使用すると, コイルを任意の位置に変更できます. 可視化のために, 以下のスクリーンショットに示すように, 一次コイルを定義するエッジも含めることができます.
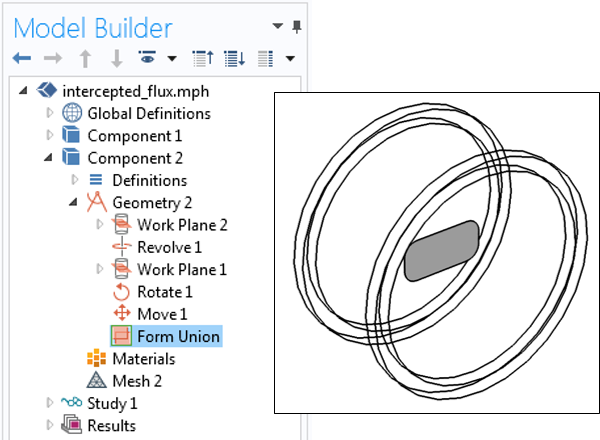
2つ目のコンポーネントとジオメトリの設定.
コンポーネント 2 の空間座標は コンポーネント 1 と完全に重なっていますが, それ以外は両者の間に接続はありません. マッピングは, コンポーネント 1 で定義されている 一般押出し コンポーネントカップリングによって導入されます. このカップリングは, コンポーネント 1 のすべてのドメインに対してソース選択を使用します. このカップリングが コンポーネント 2 の空間点で評価されるたびに, コンポーネント 1 の同じ空間点の磁場が採用されます.
2つのコンポーネントを使用し, それらの間の解をマッピングするアプローチは, シャフトのサブモデリング解析 チュートリアルモデルでも紹介されています.
コンポーネント 2 では, 2つの積分コンポーネントカップリングを定義します. 1つはピックアップコイルのエッジ上に定義され intC, もう1つは断面境界上に定義され intA です. これにより, 2つの変数を定義することで, 上記のいずれかのアプローチで相互インダクタンスを計算できます. これらの変数 L_C と L_A は, 以下の式で定義されます:
intC(t1x*comp1.genext1(comp1.Ax)+t1y*comp1.genext1(comp1.Ay)+t1z*comp1.genext1(comp1.Az))/I0
および
intA(nx*comp1.genext1(comp1.mf.Bx)+ny*comp1.genext1(comp1.mf.By)+nz*comp1.genext1(comp1.mf.Bz))/I0
ここで, t1, t1y, t1z はピックアップコイルの周囲に対する接線ベクトルの成分, nx, ny, nz はピックアップコイル表面に対する法線ベクトルの成分, I0 = 0.25 mA はグローバルパラメーターです.
モデルには複数のコンポーネントがあるため, コンポーネント 1 に含まれるコンポーネントカップリングと磁場の完全な名前を使用する必要があります. また, 法線ベクトルと周囲の接線ベクトルは, 2つの反対方向のいずれかを向く可能性があり, その結果, 符号が変化するため注意が必要です.
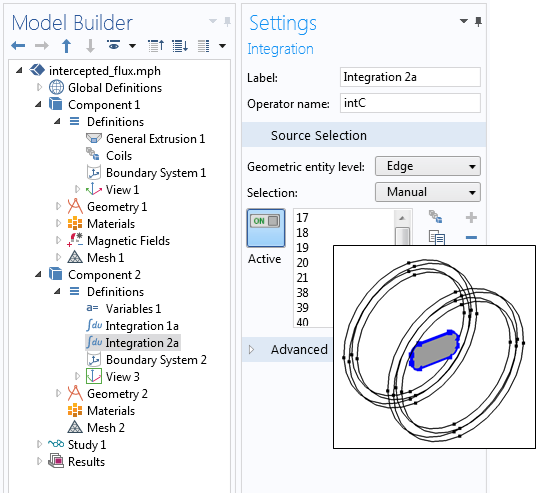
2番目のコンポーネントでは, ピックアップコイルの周囲にわたって定義された積分コンポーネントカップリングです.
ピックアップコイルの異なる位置と方向をスイープすることもできます. スタディ 1 で計算された磁場の解は既に存在します. パラメトリックスイープを含み, 物理特性を解かない2番目のスタディを追加します. スタディステップの設定で, 磁場の既存の解を使用することを指定できます (下のスクリーンショットを参照).
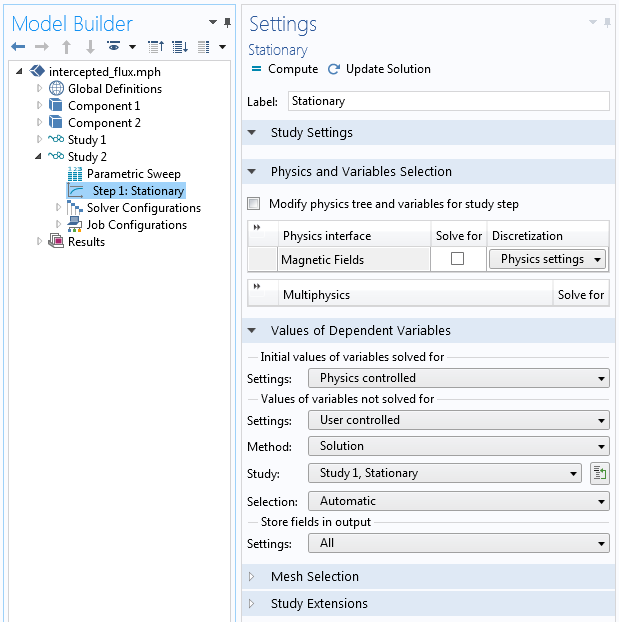
スタディ 1 の解が スタディ 2 でどのように使用されるかを示すスタディステップの設定.
この2つ目のスタディは, モデル全体を再メッシュして磁場を再計算する場合と比べて, 比較的少ない計算リソースで済みます. ピックアップコイルの各位置において, ソフトウェアはピックアップコイル表面を再メッシュするだけで済みます. スタディ 1 の解をこの新しいピックアップコイル位置にマッピングし, 2つの変数を評価します.
このアプローチは, RFID の例で示されているように, 非平面積分面や多回転積分曲線にも適用できます. 積分エッジと積分面はほぼ任意の位置に設定できるだけでなく, ジオメトリの 回転 と 移動 操作を使用して任意の位置に簡単に再配置できます. したがって, これは任意のジオメトリと位置における磁場を評価するための非常に汎用的なアプローチです.
よりシンプルなアプローチ: 切断面の使用
任意の形状に対して積分を実行できる最も柔軟なアプローチを見てきましたので, よりシンプルなケースを見てみましょう. 平面積分面を扱っており, 面エッジはその平面上の原点を基準とした x 座標と y 座標で簡単に定義できると仮定します.
このアプローチの最初のステップは, モデリング空間全体をスライス (切断面) することです. これは, 平面上の全法線フラックスの計算 に関するこちらのブログ記事で説明されているように, Cut Plane データセットを用いて行うことができます. 切断面の原点と切断面への法線ベクトルは, グローバルパラメータを用いて制御できます. また, 切断面は, それぞれローカルな x 座標と y 座標を表す cpl1x と cpl1y というローカル変数と, 切断面への法線ベクトルの成分を表す cpl1nx, cpl1ny, cpl1nz というローカル変数を定義していることにも注意してください.
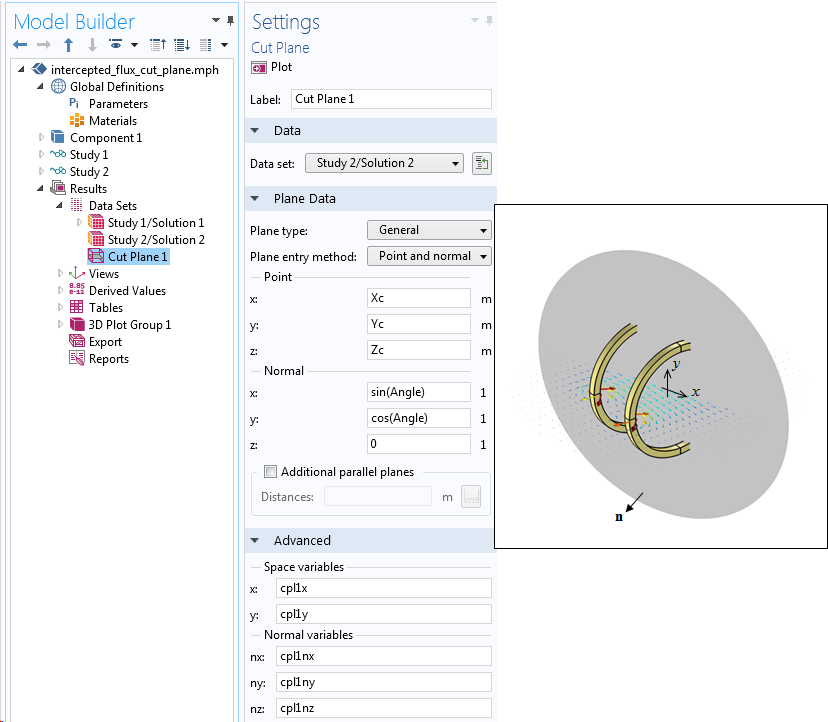
カットプレーンデータセットの使用. 原点と法線は, グローバルパラメーターを用いて定義されます. 詳細設定では, ローカルな x 座標, y 座標, および法線座標の名前が表示されます.
これで, この切断面全体にわたって面積分を実行できますが, この切断面内の部分空間に限定したいと考えています. そのためには, 対象領域内では真 (または 1 ), それ以外の領域では偽 (または 0 ) となる空間依存の論理式を使用します. この論理式は積分関数を掛け合わせます. 例えば, 下のスクリーンショットでは, 切断面上での面積分は, 次の式で表されます:
-(sqrt(cpl1x^2+cpl1y^2)<0.1[m])*(cpl1nx*mf.Bx+cpl1ny*mf.By+cpl1nz*mf.Bz)/I0
これは原点を中心とした半径 0.1 m の円内で 1 と評価される論理式 (sqrt(cpl1x^2+cpl1y^2)<0.1[m]) を含みます.
式の残りの部分は, 切断面の法線ベクトルで点付けされた流束を評価し, 切断面の原点を中心とする半径 0.1 m の円を通過する流束を求めます.
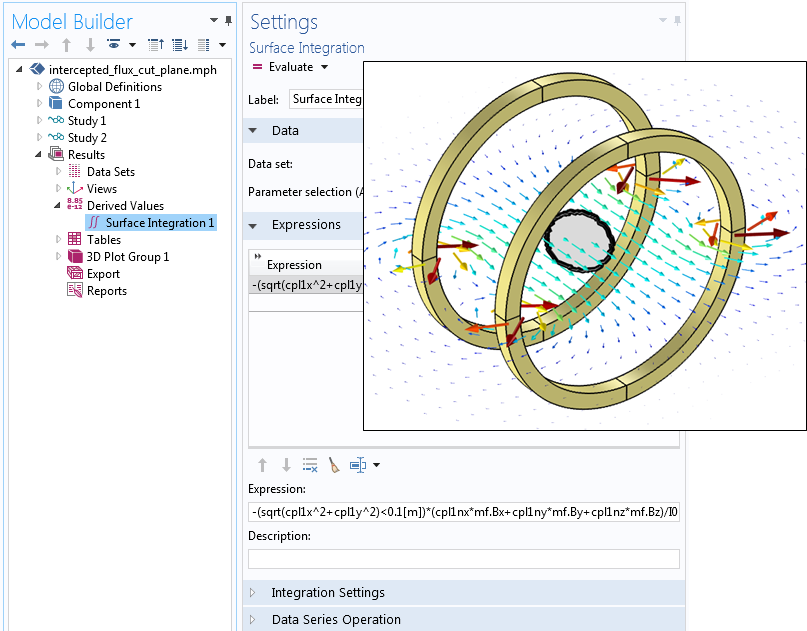
論理式を用いた切断面の部分領域における積分の評価.
切断面内の部分領域の境界は少しギザギザですが, メッシュの細分化によってこのギザギザは軽減されます. 以前のアプローチと同様に, パラメトリックスイープを用いた2つ目のスタディを使用して, 切断面の異なる方向をすべて2つ目のデータセットに保存します. この場合, 方向変更や再メッシュ化が行われる2つ目のコンポーネントやジオメトリがないため, 評価は高速になります.
さらにシンプルなアプローチ: パラメータ化された曲線の使用
次に, より小規模なケースで有用な, さらにシンプルなアプローチを見てみましょう. 媒介変数方程式 で記述できる曲線に沿って積分したいとします. 媒介変数方程式で記述できる最もシンプルな曲線の1つは, xy 平面上の単位円です. これは x=cos(s), y=sin(s) で 0\le s \le 2\pi となります. 任意のパラメトリック曲線の 接線ベクトル を計算することも簡単です. 単位円の場合, 接線ベクトルの成分は以下の通りです:
\textless \text
{tx,ty}
\textgreater = \textless-sin(s),cos(s) \textgreater
これらの簡単な方程式は, xz 平面に位置する半径 0.1 m の円の パラメーター化曲線 3D データセット内で使用できます. 円の中心点は, グローバルパラメーターセットを介してグローバル原点からオフセットされます.
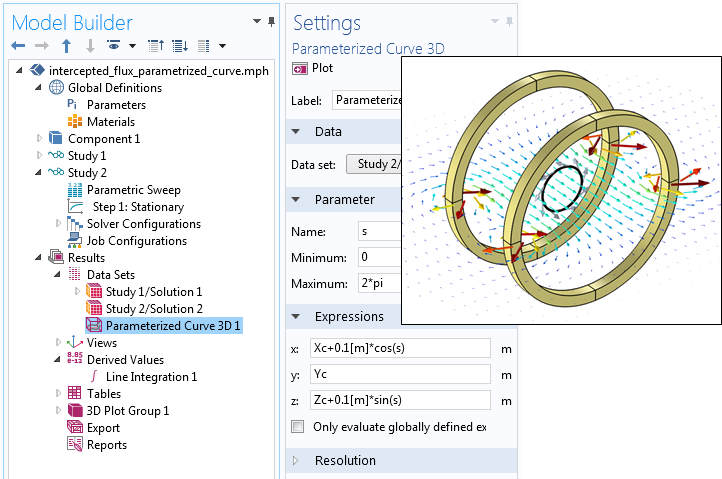
パラメトリック曲線 3D データセットの設定. 曲線は黒で, 接線ベクトルの矢印は灰色で表示されます.
別のスタディで2つ目のデータセットを作成し, パラメトリックスイープを使用して円のさまざまな原点を評価できます. 次に, 下のスクリーンショットに示すように, この新しいデータセットに対して線積分を実行します. 積分
(-sin(s)*Ax+0*Ay+cos(s)*Az)/I0
は xz 平面に円を想定し, パラメトリック曲線に沿って磁場 A を計算します.
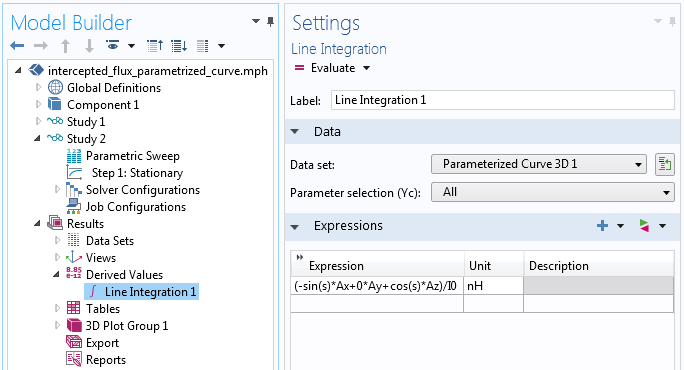
パラメトリック曲線データセット上の直線積分.
3つの手法のうち, これは与えられたメッシュ離散化に対して最も単純かつ最も正確ですが, 制限事項も最も多くあります. 座標軸に沿う円, 楕円, 正方形以外の曲線に対してパラメトリック方程式を記述するのはより困難です.
下の図は, コイル軸に沿って前後に移動する円形の積分領域について, これらすべての手法の結果をプロットし, 比較したものです.
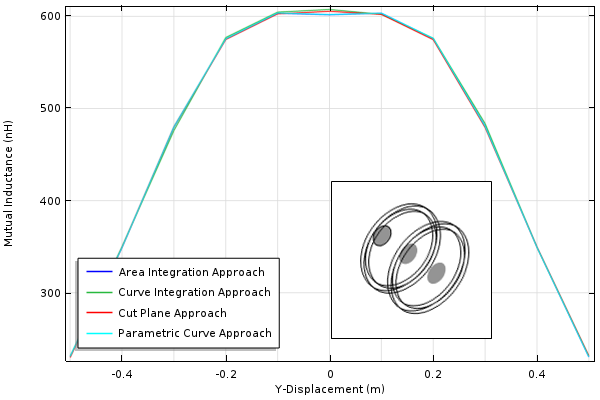
相互インダクタンスを計算するための様々な手法の比較.
任意の形状における磁場の後処理に関する結論は
ここでは, モデリング空間内の部分領域における面積分と線積分を抽出するための3つのアプローチを示しました. 最初のアプローチは最も汎用的で, 任意の (非平面を含む) 面および曲線上の積分を可能にします. また, 積分対象となる形状を任意に再配置することも可能です. このアプローチは最も柔軟性が高い一方で, セットアップに最も手間がかかります.
2つ目のアプローチ (カットプレーンデータセットを使用) は平面積分面にのみ適用可能であり, 考慮できる積分面の形状がより制限されます. 3つ目のアプローチ (パラメーター化された曲線を使用) は, 実装が最も迅速かつ簡単ですが, 円などの単純な積分曲線に最適です.
その他のリソース
- COMSOL ブログで部分領域積分について詳しく学ぶ
- 一般押出しコンポーネントカップリングの使用方法については, 以下のブログをご覧ください:






コメント (0)