
乱流モデルでは, 本質的に簡略化を伴うため, 乱流を正確にモデル化することは常に困難です. さらに, 正確なモデルは, すでに高度に非線形なモデルの収束に役立たない方程式を追加する傾向があります. この問題を解決するために, COMSOL Multiphysics® ソフトウェアのバージョン 5.3 では, v2-f 乱流モデルが導入されています. これは, 乱流境界層の異方性を記述するモデルで得られる精度と, 2方程式乱流モデルの堅牢性を組み合わせたものです.
v2-f 乱流モデルを使用した CFD のモデル化
乱流境界層における境界に垂直な運動量の輸送は, 固体壁の存在によって大きく減衰します. また, 乱流強度の垂直成分は, 平面成分よりも固体壁への近接によって強く抑制されます. つまり, 壁の垂直方向の質量および熱伝達も部分的にブロックされます. 従来, このブロッキング効果は, 壁解像乱流モデルで乱流粘性の法線成分の減衰関数を導入することで対処されてきました.
直接数値シミュレーションを使用して, Durbin は, 渦粘性の壁近傍減衰が, 次の関係に従って乱流強度の法線成分の抑制によって引き起こされることを確認しました:
(1)
ここで, Cμ はモデル定数, \[\overline {{v^2}} \] は乱流速度の法線成分の分散, T は乱流時間スケールを表します.
壁が乱流強度の減衰に与える影響は, 下の図に示されています. 泡または板状物体の表面から中心までの距離は, 泡または板状物体の中心点における乱流強度の平均を表します.
壁に近いところでは, 速度の変動は z 方向に比べて x 方向と y 方向ではるかに大きくなります. 速度の変動は異方性で, 表面は小板の形をとります. 壁から遠ざかるほど, 変動は3つの次元すべて (x, y, z) で同じ大きさになります. 速度の変動は等方性で, 表面は球状の泡の形をとります. 泡と小板の形の大きさの相対的な大きさは, さまざまな方向の変動渦の相対的な大きさを表します.
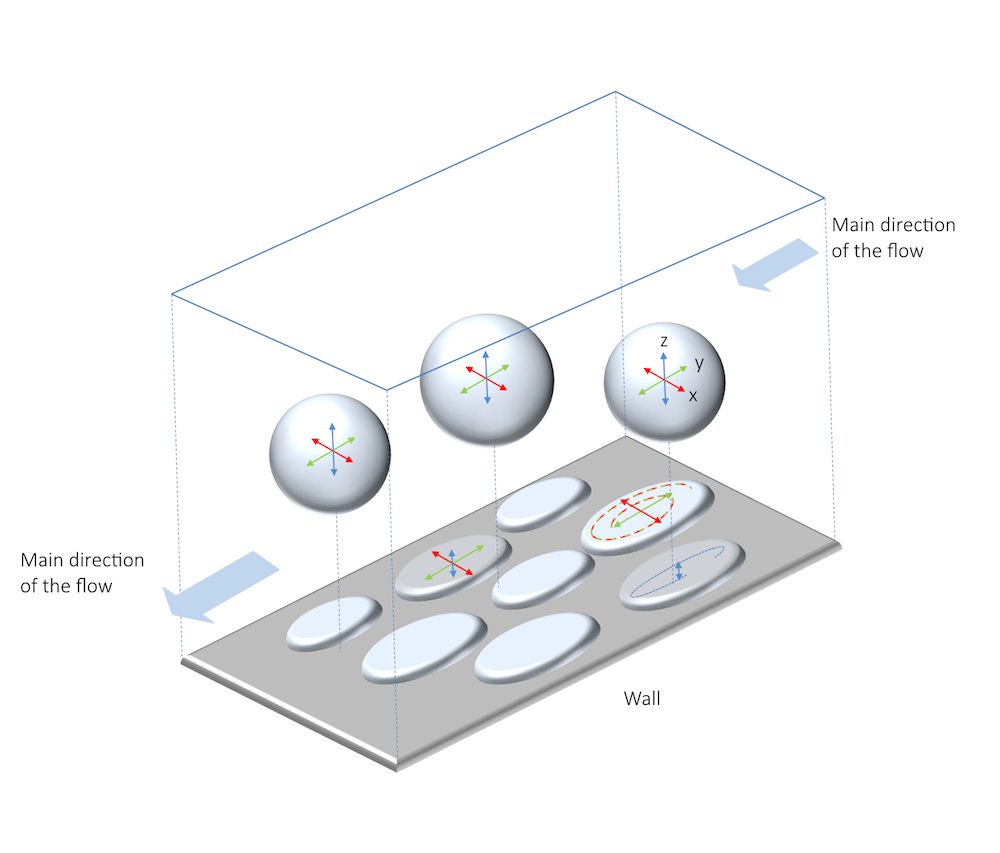
平均速度変動を仮想の泡または小板の形状として表したもの. 表面から泡または小板の中心までの距離は, 乱流強度の平均の大きさを表します.
v2-f 乱流モデルは, 乱流運動エネルギーと散逸率の2つの方程式に加えて, 2つの新しい方程式を使用して乱流境界層内の乱流強度の異方性を説明します. COMSOL Multiphysics のアドオン製品である CFD モジュールで使用される実装は, F. Billard, J. Uribe, および D. Laurence による 2008年の論文の定式化に基づいています.
v2-f 乱流モデル方程式
乱流エネルギーの輸送とさまざまな方向への乱流エネルギーの再分配を正確に記述するために, v2-f モデルでは2つの新しい方程式が導入されています. 最初の方程式は, \[{{\overline {{v^2}} } \mathord{\left/ {\vphantom {{\overline {{v^2}} } k}} \right. \kern-\nulldelimiterspace} k}\] (科学文献では通常 φ または ς と表記) に等しい変数を使用して, 壁に垂直な乱流の輸送を記述します. この方程式で, \[\overline {{v^2}} \] は乱流速度の垂直成分の分散を表し, k は乱流運動エネルギーを表します.
2番目の方程式は, 混合係数 (科学文献では通常 α と表記されます) の楕円偏微分方程式です. 楕円混合方程式は, 法線方向と平行方向の間の乱流運動エネルギーの再分配の壁誘起減衰などの非局所的効果を考慮します. 独立変数の名前から, このモデルは v2-f 乱流モデルの φ-α バージョンと呼ばれることがよくあります. このモデルは, 標準的な等方性乱流モデルと同等の堅牢性があり, v2-f モデルの元の堅牢性の低い定式化と同等の精度があります.
例 1: 周期的ヒルベンチマーク
CFD モジュールの実装は, 周期的な丘のベンチマークを含むいくつかのベンチマークケースを使用して検証されています. このモデルでは, 流れは2つの平行な丘の上に強制的に流れます. この場合, 速度場は2つの垂直な入口と出口の境界で周期的です (下の図を参照). つまり, 入口から出口の境界まで圧力降下がありますが, 速度場は同一です.
下の図では, 流れは左から右に流れています. 流れの方向の丘の後ろに再循環ゾーンが形成され, 流れが分離していることがわかります. 再循環ゾーンのサイズと入口から流れの再付着までの距離は, RANS 乱流モデルを使用して予測するのが本質的に困難です. CFD モジュールの実装で得られた結果は, 科学文献で報告された結果と非常によく一致しています.
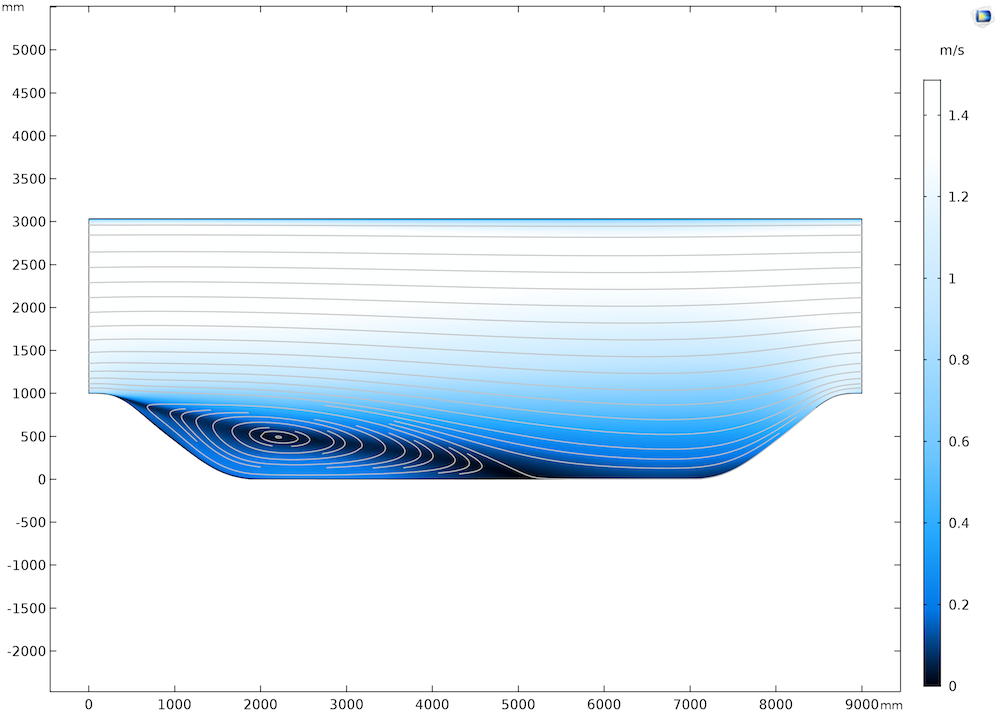
2つの丘の上の流れ. 2つの丘の頂上の垂直境界の速度プロファイルは, 入口境界と出口境界で同一です. 流れは左から右へです.
例 2: ハイドロサイクロンの流れ
もう1つの興味深い問題は, 接線方向の入口が2つあるハイドロサイクロンの流れです. 2つの出口は上部と下部にあります. 下部からの流れには通常, 不要な粒子が含まれているため, リジェクトストリームと呼ばれます. 上部の出口ストリームは, アクセプトストリームと呼ばれます. 難しいのは, 標準的な2方程式モデルでは実現できない半自由渦を捉えることです.
ハイドロサイクロンのシミュレーションの詳細については, こちらの研究論文を参照してください.
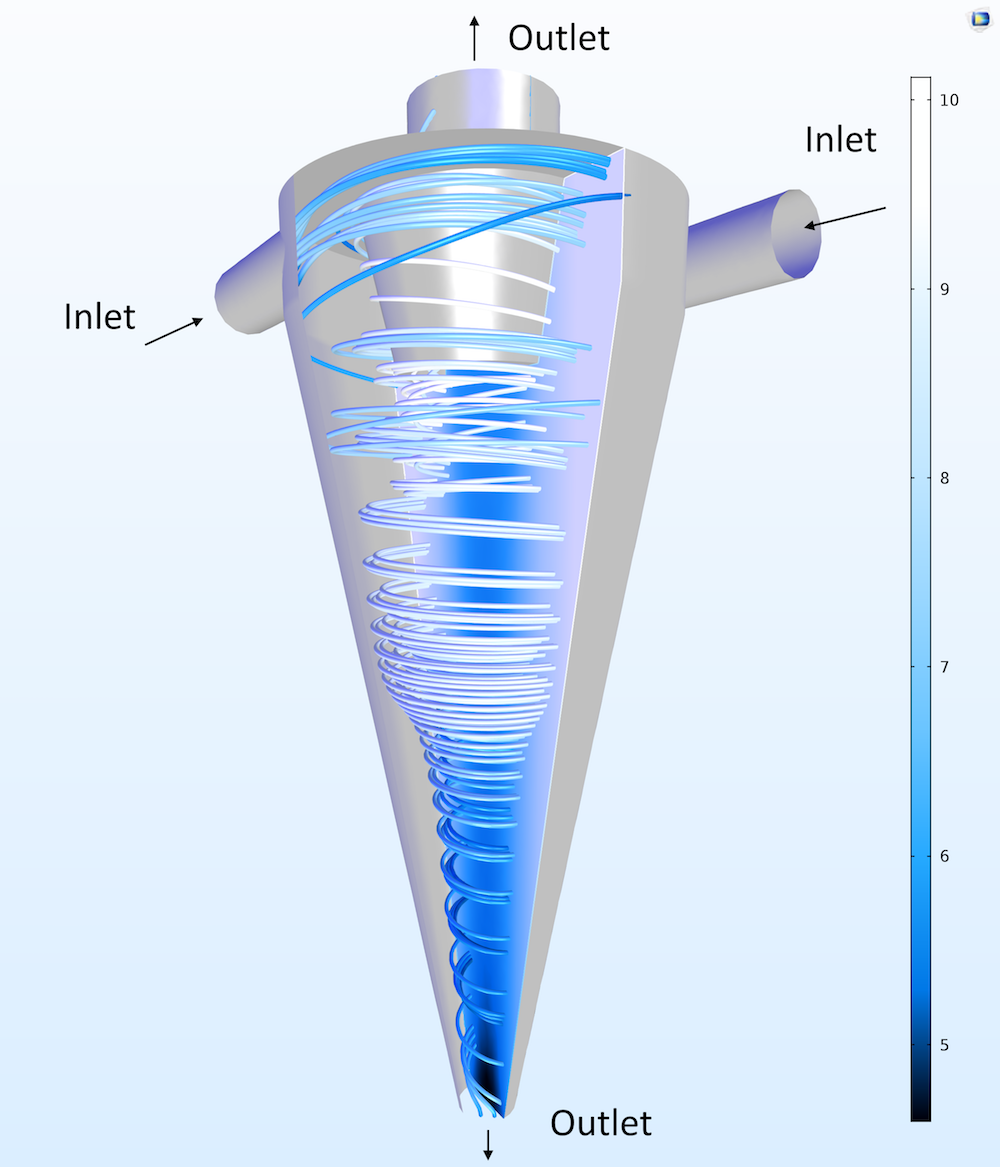
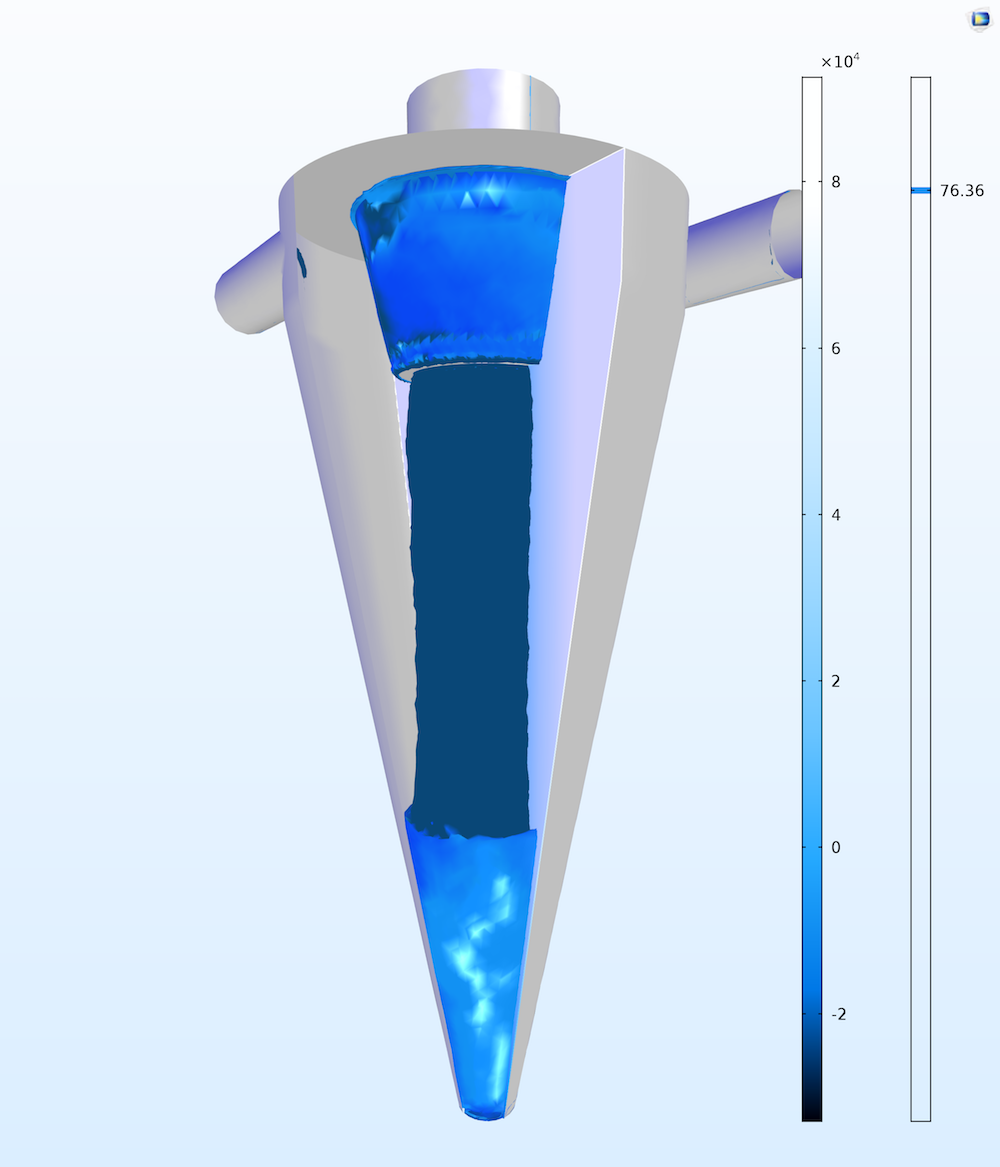
左: ハイドロサイクロン内の速度場 (流線) と圧力場 (断面プロット). 右: サイクロン内の渦度の絶対値の等値面と圧力断面. シミュレーションでは, サイクロンの中心にある自由渦を捉えています.
下の図は, 上部出口のすぐ下の速度の方位角成分を示しています. 出口パイプのすぐ外側の半径位置で最大値を示すプロファイルは, 科学文献で報告されている結果とよく一致しています. さらに, 半径に沿って最大値から外側に向かうにつれて方位角速度が減少することも, 文献とよく一致しています.
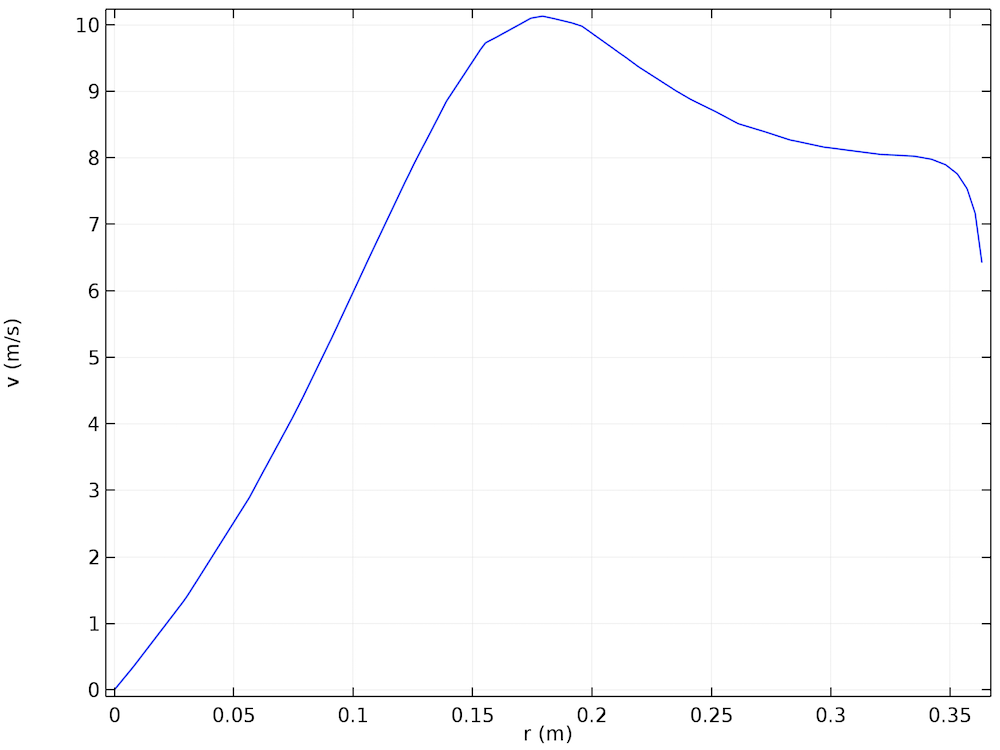
水平上部出口のすぐ下にあるサイクロンの半径の関数としての速度の方位角成分.
要約すると, 新しい v2-f 乱流モデルにより, CFD モジュールの適用範囲が広がり, 異方性乱流モデリングを必要とするケースも含まれるようになります. このモデルは, 2方程式モデルでは実現できない精度を提供しますが, 標準的な2方程式モデルと同じくらい堅牢です.
他の参考資料
- 自分で試してみましょう: ハイドロサイクロンチュートリアルモデルを取得
- CFD モジュールの更新の詳細については, リリースハイライトページ をご覧ください






コメント (0)