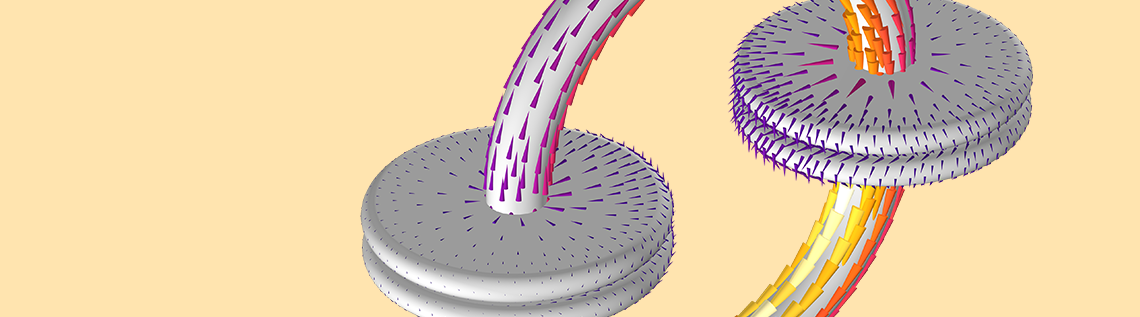
2つのコンデンサーのパラドックスは, 電気回路モデリングの限界を明らかにするために設定された挑発的な思考実験であり, このパラドックスを解決する様々な方法が考案されました. COMSOL Multiphysics®ソフトウェアでモデル化できる解決策を加え, さらに挑発的な質問をし, それに答えるために発展させます. “キャパシタンスとインダクタンスは存在するのか？” では, さっそく見ていきましょう！
2つのキャパシターのパラドックス
この思考実験は通常, 次のように表現されます. 静電容量 C を持つ 2つの等価コンデンサーが並列に接続され, その間にスイッチが開いているデバイスを考えます. すべてのワイヤーとコンデンサーは, 理想的で, 完全に抵抗がなく, 損失のない材料で作られています. コンデンサーの 1 つは電位 V_i に充電されるため, 蓄積される電荷は Q = CV_i です. もう一方のコンデンサーには電位差がないため, 蓄積される電荷はありません. スイッチを閉じると何が起こるでしょうか?
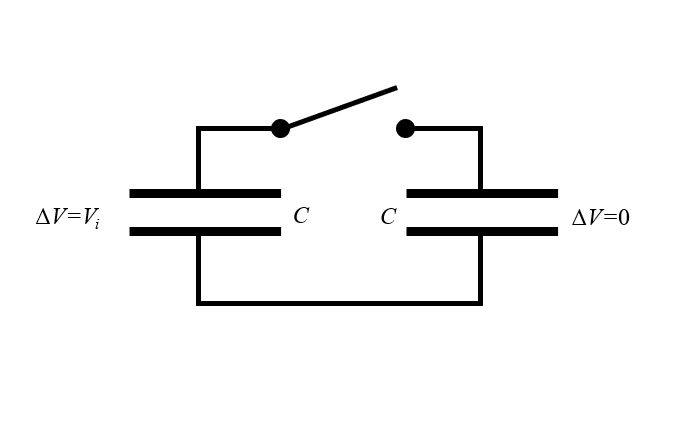
2 つのコンデンサーのパラドックスの概略図. 1 つのコンデンサーのプレート間には電位差があります. スイッチを閉じると何が起こるでしょうか.
この思考実験のプレゼンテーションの中には, 1つ目のコンデンサー上の電荷が2つ目のコンデンサーに流れ込み, 1つ目のコンデンサー上の電位差が減少し, 2つ目のコンデンサー上の電位差が増加し, 定常状態に達する—と主張するものもあります. その時点で, 電位差は両方のコンデンサー上で同じになり, 同じ電荷であるQが2つの等価なコンデンサーに広がっているため, V_iの半分になります.
しかし, これはすぐにパラドックスにつながります. なぜなら, 各コンデンサーのエネルギーは W_C = \frac{1}{2} C \Delta V^2 だからです. 初期エネルギーが \frac{1}{2} C V_i^2 で, 最終エネルギーが 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2 の場合, 残りの半分のエネルギーはどこに行くのでしょうか.
量子力学から熱力学まであらゆるものを引き合いに出す解決策は数多くあります.これらの解決策は, 教育的な観点からはおそらくすべて妥当です. しかし, その多くは, 配線やコンデンサーには単に何らかの抵抗があるか, 何らかのインダクタンスがあるはずだと述べて, 暗黙のうちに現実に訴えかけています. しかし, なぜでしょうか. 少なくとも思考実験の文脈では, 完全に損失のない材料を想定することが合理的であり, 抵抗を無視できます. しかし, インダクタンスはどうでしょうか. この思考実験の文脈では, インダクタンスを無視できるでしょうか. この質問に従って, 興味深い答えが得られるか見てみましょう.
パラドックスに対するシンプルな解決策
このデバイスは, 2つの理想的な無損失コンデンサーで構成されています. しかし, 理想的なコンデンサーであっても, 電荷を空間的に分離させる必要があります. つまり, コンデンサーにはある程度のサイズが必要です. また, 各コンデンサーにサイズがある場合, 他のコンデンサーからゼロ以外の距離で分離されている必要があります. したがって, 図を少し書き直すと, 2つのコンデンサーと, 時間によって変化する電流が流れる無損失ワイヤーの有限直径の半ループが 2つあることがわかります. しかし, このような構造を何と呼ぶのでしょうか. インダクターです.
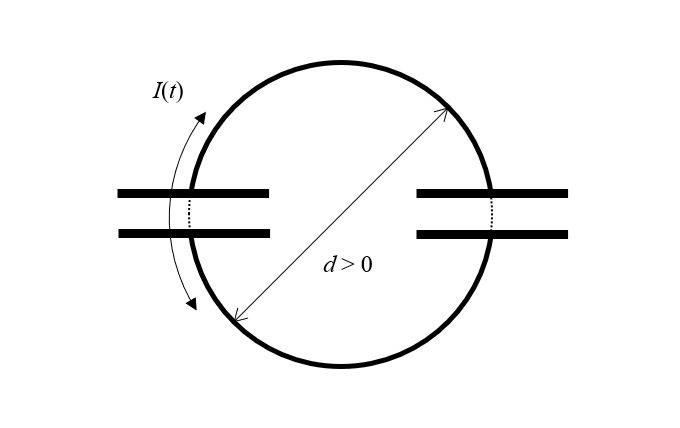
このパラドックスは, 構造のサイズがゼロ以外で, 電流が有限面積のループの周りを流れるため, インダクターでもあることを認識することで解決できます.
ここで描いた構造は有限の大きさでなければならないため, 自由空間が透磁率を持つ宇宙内に存在する限り, インダクタンスも持たなければなりません. したがって, 回路にコンデンサーがあるという単純な結果として, 回路にはインダクターもなければなりません. 実際, さらに良いことがあります. インダクターがある場合, たとえ損失のないインダクターであっても, それを流れる時間変動電流はすべて, インダクターの巻線間に電場を生じさせます. したがって, この回路に追加するインダクターはすべてコンデンサーとしても機能します. この一連のロジックを無限に続けることもできますが, ここでは, インダクタンス L を持つ単一のインダクターを使用して回路を変更するだけで十分です.
これで LC 回路が完成しました. この回路には, パラドックスを即座に解消する解析解があります. 電流はコンデンサー間を有限長のワイヤーに沿って行き来し, f=1/\sqrt{2\pi LC} で与えられる周波数で振動します.
定常解は存在しないため, 静電エネルギーのみを評価することはできません. 移動する電荷によるエネルギー, つまり電流の流れ I も考慮する必要があります. これは次のように表されます: W_L = \frac{1}{2} L I^2. この電気エネルギーと磁気エネルギーの合計 (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) は, 時間の経過とともに変化しません.
COMSOL Multiphysics® ソフトウェアによる検証
COMSOL Multiphysics® と RF モジュールを使用して, この状況を検証するモデルを構築するのは簡単です. 初期条件を計算するために, 電磁波 (過渡) インターフェースと 静電気 インターフェースを使用してこれを行います. 内部にコンデンサーと配線がある完全な真空の小さな領域をモデル化します. コンデンサーのプレート, 配線, およびボリュームの周囲の空間はすべて完全な電気導体として扱われます. つまり, 電磁場は境界を貫通しません. このような容量性放電モデルを設定するためのガイドは, ラーニングセンターの記事 “容量性放電のモデリング” に記載されています.
この時間領域モデルを解き, 電気エネルギーと磁気エネルギーの合計を評価すると, 予想どおりの振動動作が示されます. モデリング領域を複数の領域に分割して, 2つのコンデンサーの周囲の領域と周囲の空間の合計エネルギーを評価することもできます. このプロットは, エネルギーが時間だけでなく空間でも振動する様子を示しています.
コンデンサーのプレートとワイヤーの表面の電流と, その間の空間の磁場を示すアニメーション.
エネルギーと磁気エネルギーの合計は時間の経過とともに振動しますが, この損失のないデバイスではその合計は変化しません.
異なる領域における電気エネルギーと磁気エネルギーの合計は, エネルギーが時間と空間で振動していることを示しています.
これらのグラフは時間的に純粋な正弦波ではないことがわかりますが, なぜそうなるのかを問う必要があります. この高周波成分, つまり時間経過に伴うエネルギーの波紋はどこから来るのでしょうか. これは構造から生じます. 2つのプレートには明確な静電容量があることは明らかですが, ワイヤーによる電荷分離もあり, この構造全体は共振周波数を持つ円筒形の空洞内にあります. デバイスのこれらのさまざまな部分はすべて, 電磁気的動作に何らかの寄与をしています. それぞれの寄与は非常に小さいかもしれませんが, 有限サイズの構造を考えると常に存在します.
更なる質問: 静電容量とインダクタンスは存在するのか
ここで, この (または他の) 電磁装置について, より挑発的な質問をしてみましょう. この装置には静電容量とインダクタンスのどちらがあるのでしょうか. この特定の装置にはその両方があることは明らかです. しかし, コンデンサープレート間に非常に強力な誘電体を追加して改造したらどうなるでしょうか. そうすると, 静電容量は大幅に大きくなりますが, インダクタンスは変わりません. また, 静電容量を大幅に大きくした場合, インダクタンスは問題にならないと言えるのでしょうか.
簡単に言うと, 電気力学デバイスを純粋に容量性または純粋に誘導性であると考えるべきではありません. 電気力学デバイスでは, 電荷の空間的分離による電気エネルギーと電荷の移動による磁気エネルギーが常に存在します. どちらか一方を無視できる仮想的な状況を構築できる場合もありますが, 常に精神的な単純化を行っていることを忘れてはいけません.
さらに, すべての実際の材料には有限の抵抗があるため, より現実的に考えると, すべての材料にインピーダンス —があると考える必要がありますが, ここでさらに問題が発生することがあります. 周波数領域モデルを扱う場合, 電気機器のインピーダンスを表す非常によく知られた式があります.
この式における抵抗 R は, 移動する電荷の運動エネルギー, つまり電流が熱エネルギーに変換される度合いを表す尺度です.
この式は, 工学と物理学で最もよく研究されている問題の 1つです. 自由度が 1 の減衰調和振動子に関連するものとしてすぐに認識できます. この式から, このような振動子の共振周波数と品質係数を計算できること, および実際のデバイスが基本的な共振と品質係数を持っていることがわかっています. このため, この 2つを同等視し, 現実世界の有限サイズの電気デバイスを単一の抵抗, 静電容量, およびインダクタンスに縮小しようとします. これは概念上の誤りであり, 上記のインピーダンス式は極小サイズのデバイスにのみ適用できるため, 決して有効ではありません.
実際のデバイスはどれもサイズが有限で, 共振状態で動作しているときは, 上のグラフからわかるように, 電気エネルギーと磁気エネルギーが空間と時間で変化します. したがって, 等価回路モデルには少なくとも 3つのノードが必要ですが, 場合によってはそれ以上のノードが必要になります. 2つのコンデンサーの物理モデルに戻って, 各コンデンサーのプレートが電気回路のノードで表されていると仮定すると, 等価回路モデルは少なくとも下図の 4つのノードを持つ回路と同じくらい複雑になる必要があることがわかります. ワイヤーに沿って電荷が分離されるため, ワイヤーのインダクタンスに並列に小さな静電容量が追加されていることに注意してください.
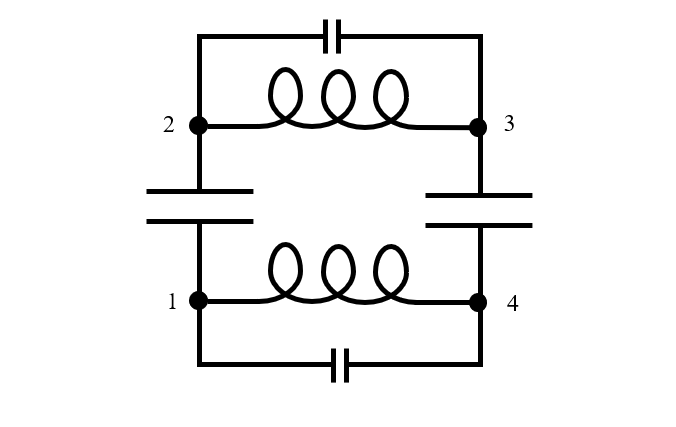
直列に接続された 2 つの有限サイズの無損失コンデンサーの等価回路モデル
この例から, 共振付近で有効な等価回路モデルの構築はすぐに非常に複雑になり, 物理的な洞察, 同様のデバイスに関するかなりの経験, および数値モデリングが必要になることがわかると思います.
元の質問に戻ると, 静電容量, インダクタンス, さらには抵抗も, それ自体では存在しない概念であり, 互いに組み合わさってのみ存在すると主張できます. デバイスの周波数依存インピーダンスを単一の抵抗, 静電容量, および/またはインダクタンスにまで減らすことができる場合もありますが, このような単純化はデバイスの共振周波数より低い周波数でのみ有効です. これを念頭に置いておくと, この面白い 2つのコンデンサーのパラドックスから, はるかに苛立たしいほど複雑な現実世界の問題に至るまで, あらゆる種類の落とし穴を回避するのに役立ちます.
おわりに
ここでは, 共振付近で動作する電磁気装置のインピーダンスを単一の等価抵抗, 静電容量, およびインダクタンスに分解できない理由を理解するために, 古典的な思考実験を使用しました. 2つのコンデンサーのパラドックスのような思考実験は, 電磁気学の理解を広げ, 計算モデルの結果を解釈する上で役立ちます.
参考文献
モデリングとシミュレーションを使用して他の難問を解決する方法を知りたいですか? COMSOL ブログで他の例をいくつか確認してください.
コメント (0)