
私は最近, Knowles Electronics の Wade Conklin 氏と Jordan Schultz 氏とともに, 第166回アメリカ音響学会 (2013年秋) にちょっとした論文を寄稿する機会に恵まれました. Wade 氏は, “Characterization of a microelectromechanical microphone using the finite element method” と題する論文を発表しました. この発表は, COMSOL Multiphysics を使用して Knowles MEMS マイク (SPU0409LE5H マイク, 下の写真を参照) の仮想プロトタイプを実装するというものでした.

寸法 3.76 x 3 x 1.1 mm3 の Knowles SPU0409LE5FH MEMS コンデンサーマイク. 写真は Knowles Electronics 提供.
MEMS マイクとは?
MEMS マイクは, 音響ハウジングに組み合わされた MEMS ダイと相補型金属酸化膜半導体 (CMOS) ダイで構成されるコンデンサーマイクです. CMOS には, プリアンプとアナログ/デジタル (AD) コンバーターの両方が含まれていることがよくあります. このため, またマイクのサイズが小さいため, デジタルモバイルデバイス, スマートフォン, ヘッドセット, 補聴器への統合に適しています. 音響ポートを備えたハウジングは, 上の画像に示されています. コンデンサーまたは可変コンデンサーは, 穴の開いた剛性のあるバックプレートに近接した非常に柔軟なダイヤフラムで構成されています. 穴により, ダイヤフラムとバックプレートの間の空気が逃げることができます. ダイヤフラムとバックプレートのペアはモーターと呼ばれます (下の図に示されています). マイクは, 最初にコンデンサーを DC 電圧で分極 (充電) することで機能します. この電圧により, ダイヤフラムの静的変形と張力も発生し, バックプレートにも影響はごくわずかです. 音響信号が音響ポートを通じてダイヤフラムに到達すると, ダイヤフラムが動き始めます. この機械的な変形により, マイクロフォン全体に AC 電圧が発生します. これらの効果を組み合わせることで, COMSOL Multiphysics での解析に適した実際のマルチフィジックス問題が実現します. マイクロフォンの感度は, 入射圧力と測定電圧の比として dB スケールで表されます.
Knowles MEMS マイク仮想プロトタイプについて
MEMS マイクモデルには, トランスデューサーの電気的, 機械的, および音響的特性の説明が含まれています. 音響の説明には, 熱損失と粘性損失が含まれており, 線形連続性, ナビエ・ストークス, およびエネルギー方程式を陽的に解く, つまり 熱音響 です. 振動板の力学も, 静電引力と音響負荷, つまり 電気機械 を含めてモデル化されました. 振動板とマイクのバックプレートの小さな穴との相互作用を分析するために, サブモデル も実装されました. このモデルにはフリーフィッティングパラメーターがなく, MEMS モーター (振動板とバックプレート系) の静的機械的動作と動的周波数応答を予測できました. モデルの結果は, 測定データとよく一致しました.
音響および MEMS モジュールによるモデリング
この系では幾何学的寸法が非常に小さいため, 振動板の振動は空気によって大きく減衰します. 空気と音響は, 熱伝導と粘性損失の両方を考慮して処理する必要があります. 粘性浸透深さ (音響粘性境界層の厚さ) は, たとえば 100 Hz で 55 µm, 10 kHz で 5.5 µm であり, これはバックプレートと振動板の間の距離 (わずか 4 µm) よりも大きいか, 同等です. 音響モジュール の 熱音響 インターフェースは, これらの効果をモデリングするための自然な第一選択です. このインターフェースにより, 低周波数での断熱動作から等温動作への移行も正しくモデリングできます. 複雑な複合力学と静電気効果はすべて, MEMS モジュール の 電気力学 インターフェースに含まれています. 2つの物理現象は, 変位/速度場の連続性を要求することにより, 流体構造境界で完全に結合されています.
MEMS マイクは複雑な系を構成するため, 詳細にモデル化しようとするといくつかの課題に直面しました. その一部は次のとおりです:
- クリーンルーム MEMS 製造プロセス中に, ダイヤフラムが解放され, わずかに曲がります
- 初期形状と応力分布を正しく記述することが重要です
- マイクの形状は複雑で, さまざまなアスペクト比と小さな長さスケールが関係します
- メッシュについて考えることが重要です
- 系が複雑で, さまざまな物理特性が関係するため, 結果として得られるモデルは簡単に大きすぎて求解できなくなります
- 対称性と集中近似を使用してモデルを縮小することも検討する必要があります
モデルギャラリの B&K 4134 などの従来のコンデンサーマイクは, 本質的に同じように機能します MEMS マイクと同じ方法で, 同じ物理を解く必要があります. ただし, モデリングには, 前述のようにいくつかの特定の課題があります. 主な課題は, 複雑な製造工程と, 初期の静的状態と形状の複雑さの記述にあります.
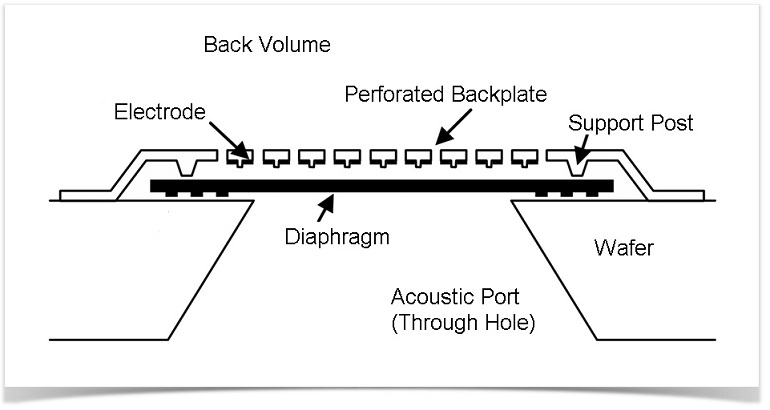
MEMS マイクモーターのスケッチ (縮尺ではありません). ダイヤフラムの厚さは 1 µm, バックプレートとダイヤフラムの隙間は 4 µm, バックプレートの穴の直径は 10 µm, バックプレートの厚さは 2 µm です. モーターの支柱から支柱までの距離は 590 µm です. スケッチは Knowles Electronics の提供です.
COMSOL モデルの結果の一部
モデリングプロセスを計画する際の最初のステップとして, モデルの初期定常記述の検証に重点を置くことにしました. マイクロフォンの定常形状を直接測定するには, DC 静電容量を分極電圧の関数として測定します. 測定値は, 下の図でモデルの結果と比較されています. ご覧のとおり, 2つの曲線はよく一致しています. 約 15.8 V で, 測定された曲線が急上昇しているのがわかります. これは, 静電気力によってダイヤフラムが大きく曲がり, バックプレートに接触するポイントに対応しています.
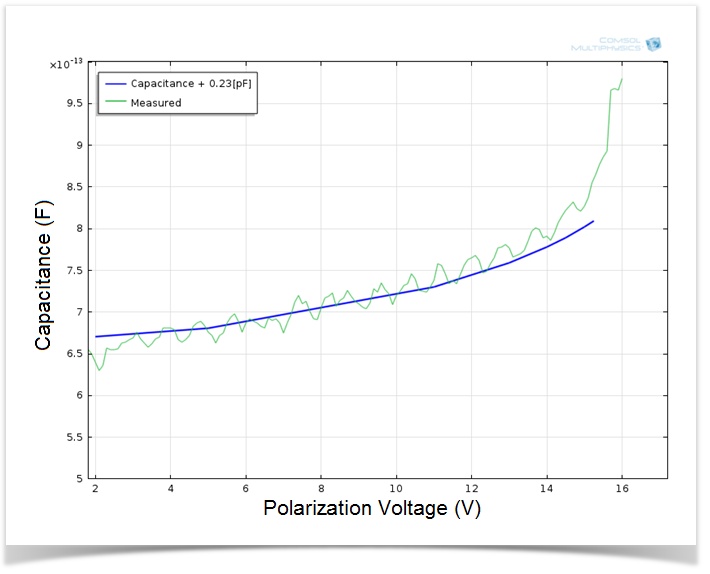
DC 分極電圧の関数としてのマイクの静電容量のシミュレーション結果. 緑色 の曲線は測定値を表し, 青色 の曲線は, 測定の実行時に存在する一定の寄生容量 (0.23 pF) を考慮した定数オフセットを含むモデル化された静電容量を表します. 測定値は Knowles Electronics の提供によるものです.
下の画像には, マイクロフォンモーターの30度の断面をスライスした際の電位が示されています. 電極が配置されている領域では電場の勾配が非常に強く, この領域外では低下していることがわかります. バックプレートの穴が電場に影響を与えているのは明らかです. マイクロフォンの完全な動的動作も, 周波数領域で構造変位, 電場, 熱音響場 (圧力, 速度, 温度) を解析して解析されました. これは複雑な形状の完全に結合されたマルチフィジックスモデルであるため, 解析には最大 60 GB の RAM が必要でした. 結果の感度も測定値とよく一致しました.
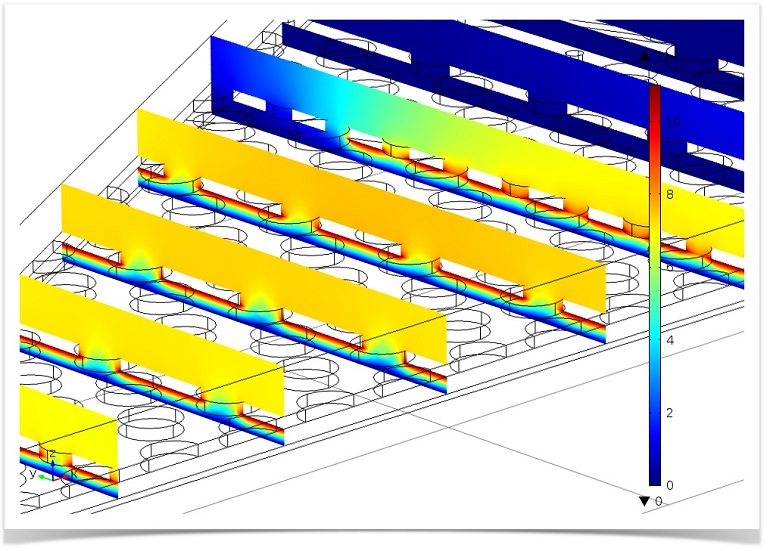
MEMS マイクモーターを通したスライスで描かれた定常電位.
ダイアフラムとバックプレート系のユニットセルが, 以下のアニメーションに示されています. モデルは, 振動するダイアフラムとバックプレート (ここでは固定) 間の1つの穴とエアギャップ (薄い空気膜) を表しています. この系は, 対称性を使用してユニットセルとして解析されます. 粘性損失と熱損失を含む詳細な結合音響挙動は, 熱音響 インターフェースを使用して再び捕獲されます. 2つのアニメーションは, 10 kHz での瞬間的な音速分布と温度分布の1周期にわたる挙動を示しています. モデルは圧力も計算します (ここでは示されていません). アニメーションでは, 熱境界層と粘性境界層の両方の増加と減少を見ることができます. 10 kHz では, 両方の厚さは約 5 µm で, エアギャップの高さ 4 µm に匹敵します.
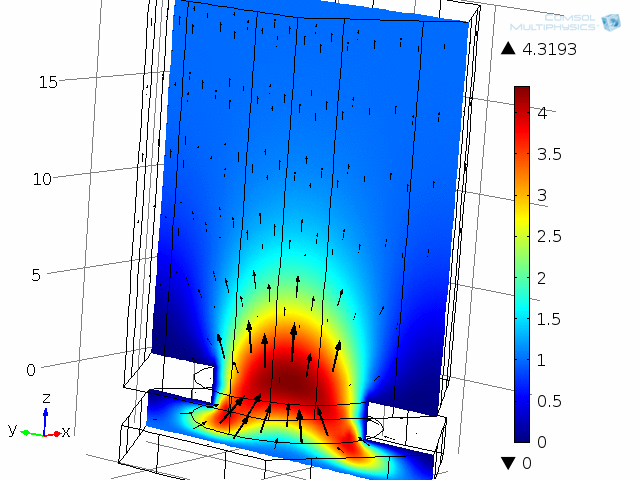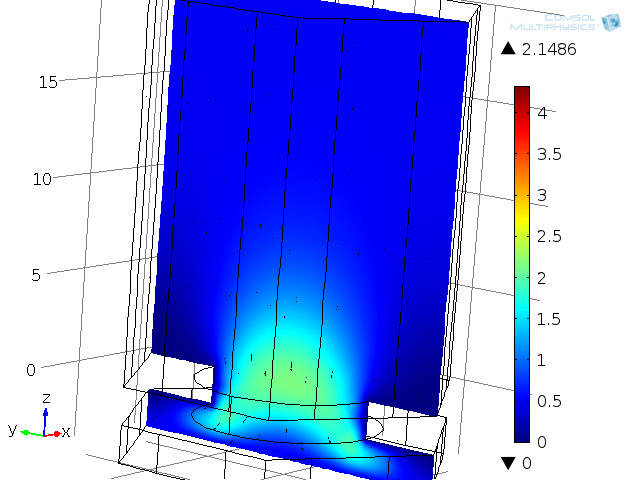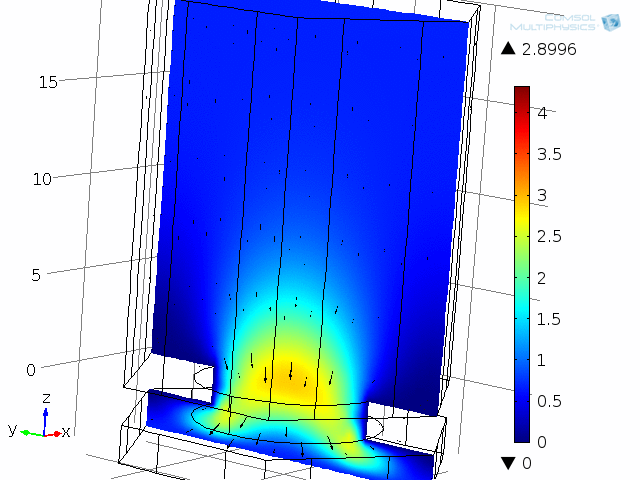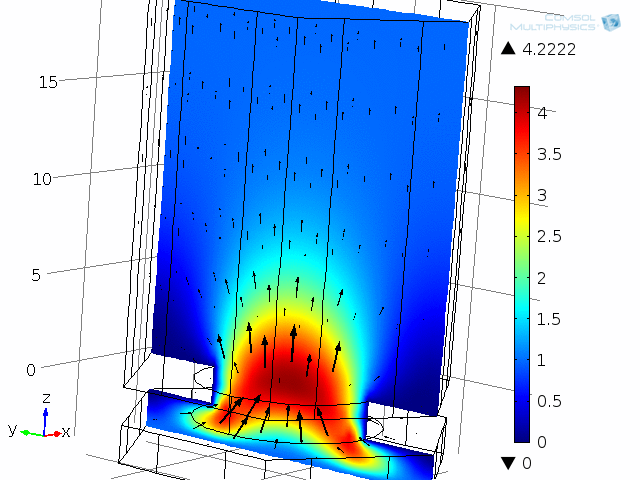
ここでは 10 kHz でモデル化された, ダイアフラムとバックプレート系の1つの “単位セル” の動的解析. ここには, 瞬間音響速度の大きさ (色) と速度場 (ベクトル) が表示されています.
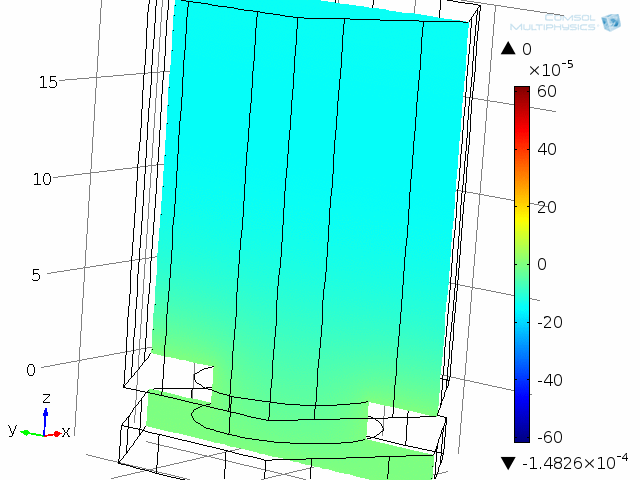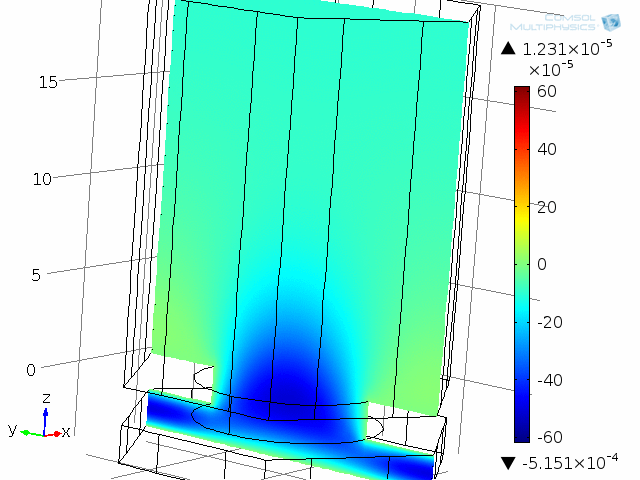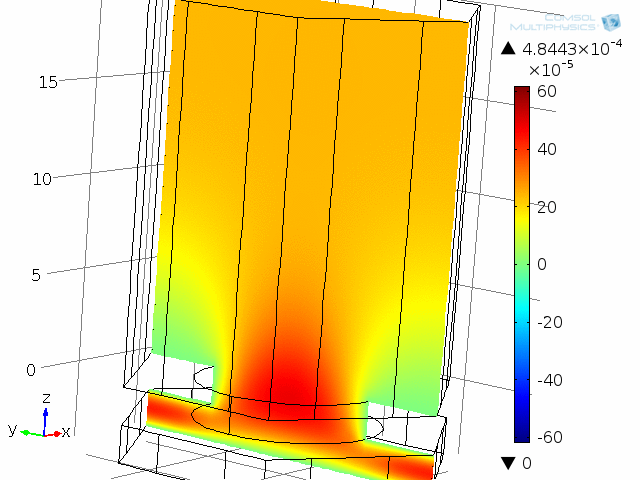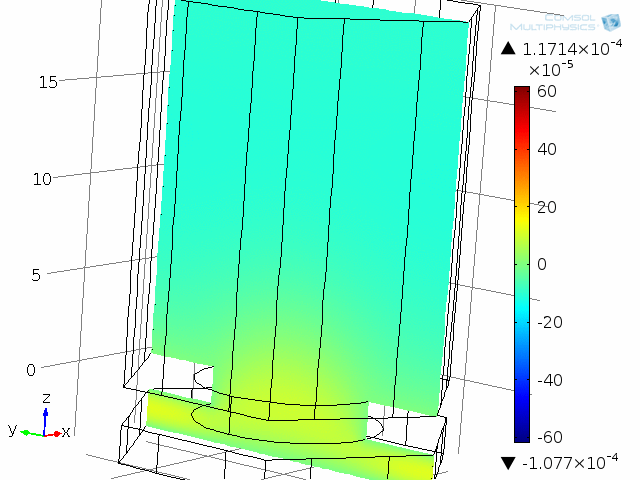
ここでは 10 kHz でモデル化された, ダイアフラムとバックプレート系の1つの “単位セル” の動的解析. 音響温度変化はこのアニメーションで示されています.
その他の資料
- M. J. H. Jensen, W. Conklin, and J. Schultz, Characterization of a microelectromechanical microphone using the finite element method, J. Acoust. Soc. Am., 134, pp. 4122 (2013) (Conference abstract)
- B&K 4134 コンデンサーマイクモデル (モデルギャラリ内)
- Knowles Electronics
- 音響モジュール
- MEMS モジュール
- P. Loeppert and S. Lee, Sisonic–the first commercialized MEMS microphone, Solid-state sensors, actuators and microsystems workshop, Hilton Head Island, South Carolina, pp. 27–30 (2006)






コメント (0)