フィレットを施すべきか, 施すべきではないか. それがマルチフィジックス解析者を悩ませる問題です. 有限要素モデルを構築する際, 鋭角なエッジは局所的な特異点や, メッシュ細分化に伴う非収束性の場を引き起こす可能性があります. フィレットを追加してこれらの鋭角を丸めることで, この特異点を回避できます. 実際, 多くのマルチフィジックスモデルでは, これらの鋭角とその結果生じる特異点は必ずしも結果に悪影響を与えるわけではありません. 詳しく見ていきましょう.
鋭角コーナー周辺の電磁加熱
COMSOL Multiphysics® ソフトウェア で解く最も一般的な問題の一つは, 電磁加熱の問題です. これは, 電流の流れとそれに伴う損失を解くマックスウェル方程式の解と, 温度分布を解く伝熱方程式の解を組み合わせます.
以前のブログ で述べたように, 電磁場を解く際に, 鋭角な凹角は局所的に非収束性の電場と電流密度をもたらします. 電磁損失は電場と電流密度の積であるため, 鋭角部におけるピーク損失はメッシュを細分化すると同様に無限大に近づきます.
しかし, 鋭角部周辺の損失の積分は, メッシュを細分化すると収束します. これは有限要素法の強みの一つであり, 支配方程式をいわゆる 弱形式 で解きます. これは支配偏微分方程式を積分的に満たします. つまり, モデル全体の誤差を最小化しつつ, 局所誤差 (場合によっては無限大!) を許容することになります.
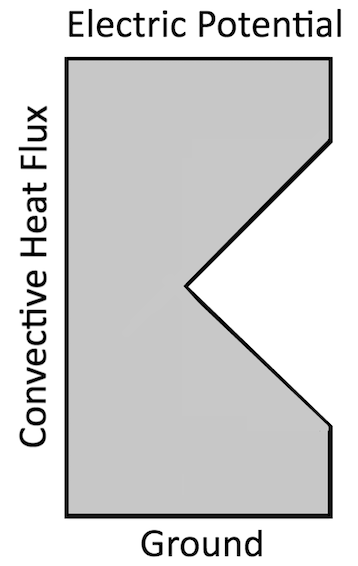
鋭角部内側に特異点を持つ単純な電磁加熱問題の模式図.
上の図に示すような簡単な例でこの概念を確認してみましょう. 鋭いノッチを持つ長方形領域に電位差を与えると, 材料に電流が流れ, 抵抗損失が発生します.
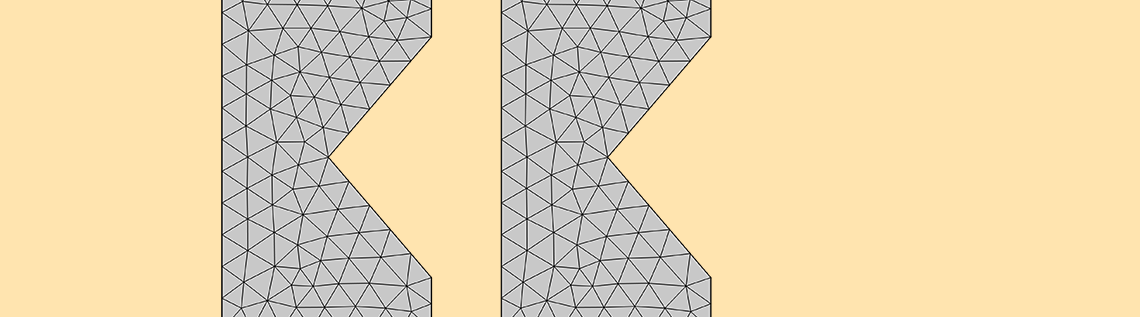
下図は, 鋭角部内側におけるメッシュ細分化レベルの違いによる抵抗損失とメッシュのカラープロットです. メッシュを最高レベルで細分化すると, 損失は鋭角部の周囲に非常に局所的に現れます.
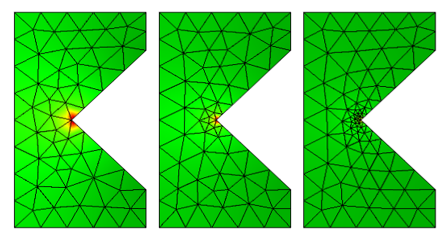
複数の異なるメッシュにおける電磁損失.
この鋭角な内側の角では, この形状と境界条件から, 電流はある点で瞬時に方向を変える必要があるため, 電場は理論上は無限大になります. また, 鋭角な外側の角は特異点を生じないことにも注意してください. 形状と境界条件の結果として, これらの点では電流の方向が瞬時に変わることはありません.
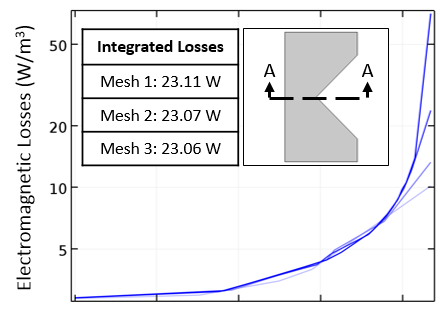
切断線に沿ってプロットされた対数スケールの抵抗損失と, 異なるメッシュにおける損失の積分の表.
上に示すように, 断面線で損失をプロットすると, メッシュを細分化するにつれて, 鋭角点における損失が徐々に大きくなることがわかります. しかし, 領域全体 (おおよそプロットされた曲線の下の領域) における損失の積分は, メッシュの細分化とともに非常に急速に収束します.
ここで, 定常状態における温度分布の熱伝達方程式を追加的に解くことで, これをマルチフィジックス問題にしてみましょう. これらの温度場は, メッシュ細分化レベルごとにプロットされており, 鋭角点における温度も示されています.
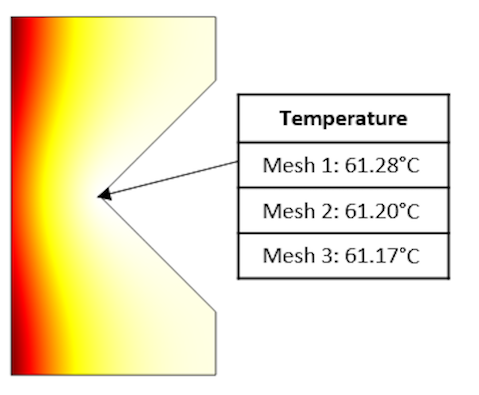
様々なメッシュ細分化レベルにおける鋭角点での温度場と温度テーブル.
これらの結果から, 特異点の温度, そしてもちろん他のすべての温度も, メッシュ細分化の影響をほとんど受けないことがわかります. これには2つの理由があります. 第一に, 先ほど見たように, 総抵抗損失はメッシュの影響をほとんど受けません. 第二に, 定常熱伝達支配方程式の拡散特性により, 総熱負荷が同程度であれば, 非常に似た温度解が返されます. 一方, 非定常温度解は, 熱負荷が非常に高い場合, 局所的に非常に高い温度を予測する可能性がありますが, これは時間的制約ではあるものの, 局所的かつ相対的な影響です. つまり, 空間における熱負荷分布の急上昇は時間の経過とともに平滑化され, シミュレーション時間が非常に長い場合, 非定常解は定常解に近づきます.
まとめ
この情報から何が言えるでしょうか? 電磁加熱問題を解き, 総電磁損失と温度分布の計算のみに関心がある場合, 通常はモデルにフィレットを追加する必要がありません.
この方法には2つの利点があります. まず, CAD モデリングのようにジオメトリにフィレットを追加する手間がかからず, また, 鋭角部のメッシュを過度に細分化する必要がないため, 最も貴重なリソースである時間を節約できます!






コメント (0)