
前回のブログでは, 電子エネルギー分布関数 (EEDF) の種類と, プラズマモデリングにおけるその重要性について紹介しました. 本日は, ボルツマン方程式 (2項近似) インターフェースに注目し, アプリケーションライブラリの例を用いて, その使用方法を説明します.
編集部注: このブログのオリジナル版は2015年4月8日に公開されました. その後, COMSOL Multiphysics® ソフトウェアのバージョン 6.0 の新機能を反映するために更新されました.
ボルツマン方程式の紹介 (2項近似) インターフェース
プラズマモデルでは, 電子のエネルギー分布関数だけでなく, 電子の輸送特性 (電子移動度など) も必要です. 最も単純なケースでは, マックスウェル型 EEDF と電子移動度の一定値を使用することができます. その後, その他の輸送特性は, COMSOL Multiphysics でアインシュタインの関係式を使用して計算されます. しかし, 場合によっては, ボルツマン方程式の解から得た EEDF を使用し, 電子輸送特性を平均電子エネルギーの関数として定義することが有利になることがあります. しかし, このデータをどのように入手すればよいのでしょうか.
その答えは: COMSOL Multiphysics のボルツマン方程式 (2項近似) インターフェースです. このインターフェースの使用例はアプリケーションライブラリに掲載されており, そのうちの 1 つがアルゴンボルツマン解析モデルです. 2項近似でボルツマン方程式を計算するためには, プラズマの電離度などのパラメーターが必要です. これらのパラメーターは先験的に分かっているわけではありません. 従って, その手順は反復プロセスです.
このプロセスは, まずパラメーターの初期推測を行い, ボルツマン方程式を解くことから始まります. 次に, 必要に応じて EEDF と輸送特性をプラズマモデルにインポートします. 最後に, プラズマモデルを計算し, プラズマモデルからの新しいパラメーターでボルツマン方程式を再求解します. 収束に達するまでこれらのステップを繰り返し続けることができます.
それでは, プラズマモデルへのデータの作成, エクスポート, およびインポートの手順を説明します.
電子エネルギー分布関数と電子伝達特性
ボルツマン方程式 (2項近似) インターフェースからデータを作成
最初のステップは, 2項近似でボルツマン方程式を解くことによってデータを作成することです. 次の図は, このステップで使用される2項近似インターフェースであるボルツマン方程式のスクリーンショットを示しています. 電子エネルギーに対して一定の最大エネルギー値を定義する必要があります. この例では, これは Emax = 100 V に設定されています. さらに, ある範囲の平均電子エネルギーの EEDF を計算するには, 平均エネルギーのスタディが必要です.
次の図は, いくつかの平均電子エネルギーに対するアルゴンプラズマで計算された EEDF を示しています. プラズマは 400 K のガス温度, 1018 1/m³ の電子密度, 10-6 のイオン化度, および 0.01 % の励起アルゴンのモル分率を特徴としています. EEDF は電子エネルギーの関数であることがわかります.
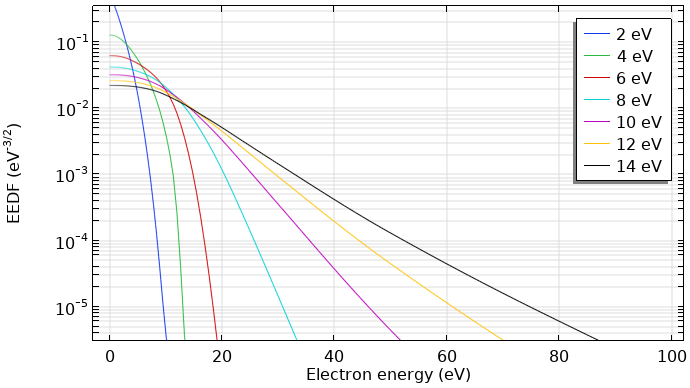
アルゴンプラズマで計算された EEDF.
次の図は, ボルツマン方程式 (2項近似) インターフェースを使用して計算された対応する還元電子輸送特性を示しています. データは平均電子エネルギーの関数です.
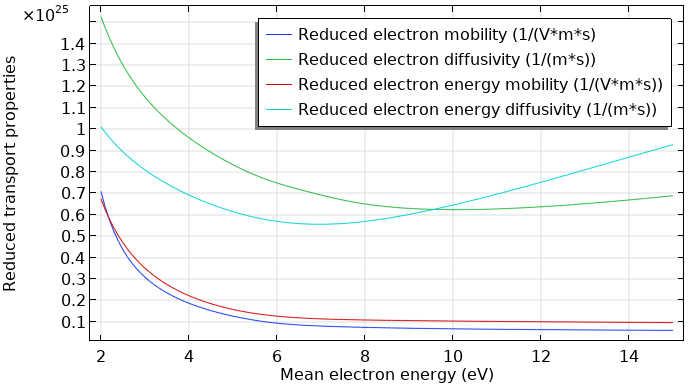
アルゴンプラズマにおける還元電子輸送特性.
ボルツマン方程式 (2項近似) インターフェースからのデータのエクスポート
EEDF は, 3行で構成されるスプレッドシートとしてプラズマモデルにインポートする必要があります. 最初の行 (x データ) は電子エネルギー (eV) である必要があり, 2番目の行(y データ)は平均電子エネルギー (eV) である必要があります. 一方, 3行目には, 分布関数の値 (eV^(-3/2)) が含まれている必要があります. 最後に, 次の画像のような 2D プロットをエクスポートする必要があります.
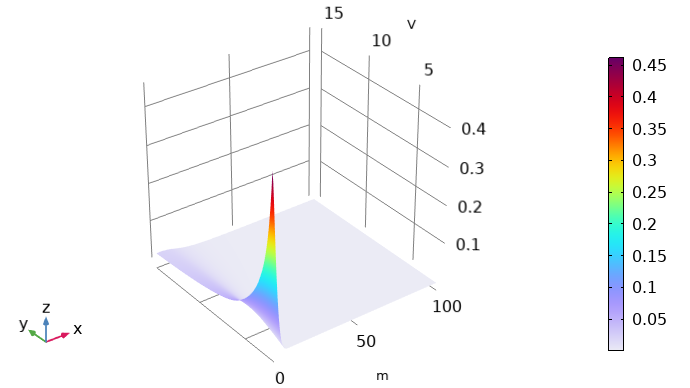
計算された EEDF の2D プロット. ここで, x 軸は電子エネルギーを示し, y 軸は平均電子エネルギーを表します. 色は, 分布関数の値を示しています.
単位に関する注意: プラズマモジュールでは, 電子エネルギーと電子平均エネルギーは V の単位で表示されますが, 内部では eV として扱われます. したがって, このコンテキストでは, V は eV として読み取る必要があります. 電子エネルギーを表し, EEDF が求解される追加の次元はメートル単位で表示されますが, 内部では eV として扱われます.
EEDF を目的の形式でエクスポートするには, パラメトリック押出しデータセットを使用します. パラメトリック押出しは, パラメーター (この場合は平均エネルギー) を使用してデータセットを拡張します. データセットを右クリックして, パラメトリック押出し1D を選択します.
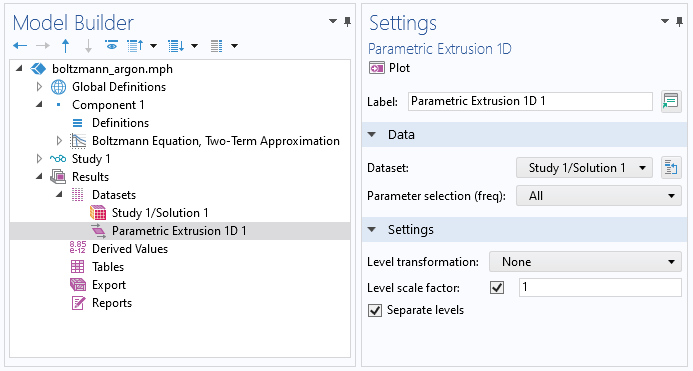
ボルツマン方程式 (2項近似) インターフェースは, 0D インターフェースであり, 1D 軸上の電子エネルギーを表すために追加の次元を使用します. 追加のディメンションは最大エネルギー値に正規化されるため, データをエクスポートする前に, 最大エネルギー値で手動によりスケーリングする必要があります. これを行うには, 変換データセットを使用できます. 変換データセットを使用すると, データセットをスケーリング, 回転, および移動できます. したがって, データセットを右クリックして, 変換2D を選択します. x スケールを最大エネルギー (この場合は Emax) に設定します.
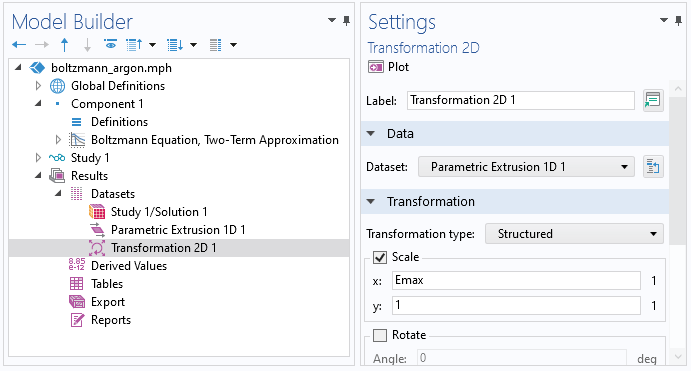
次に, 変換2D データを右クリックし, エクスポートするデータの追加を選択します. 式ウィンドウに be.f と入力します. ファイル名を選択し, エクスポートをクリックします.
輸送特性は, それぞれの1D プロットから簡単にエクスポートできます. 1D プロットのグローバルノードを右クリックし, プロットデータをエクスポートに追加を選択します. ファイル名を選択し, エクスポートをクリックします.
プラズマモデルへのデータのインポート
EEDF をプラズマモデルにインポートするには, 補間関数を作成します. データソースとしてファイルを選択し, 引数の数フィールドに2を入力します. 参照をクリックして, ファイルをインポートします.
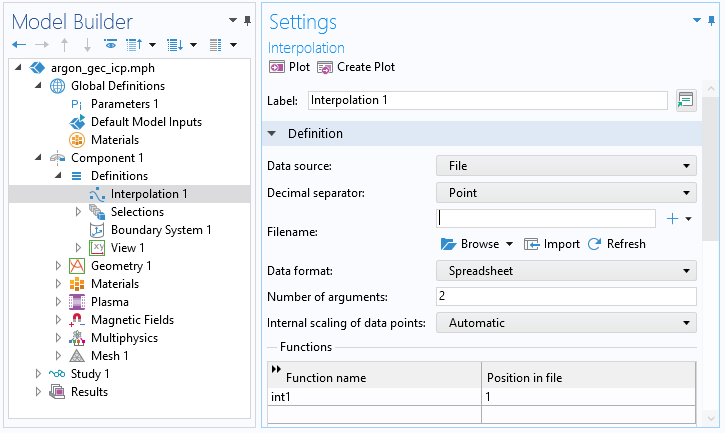
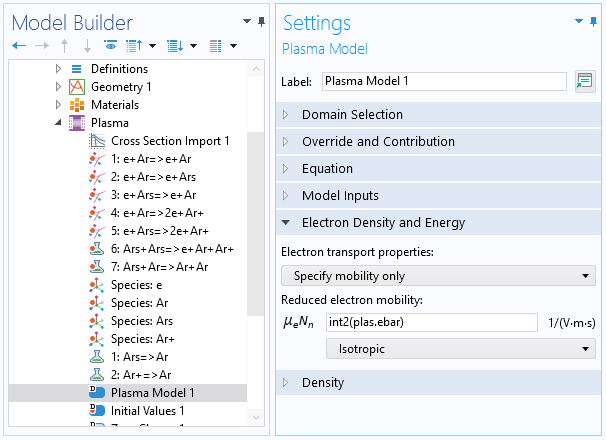
これを実行すると, プラズマモデルのメインノード電子エネルギー分布関数設定で, 内挿関数を EEDF として選択できます. これは, 以下のスクリーンショットに示されています.
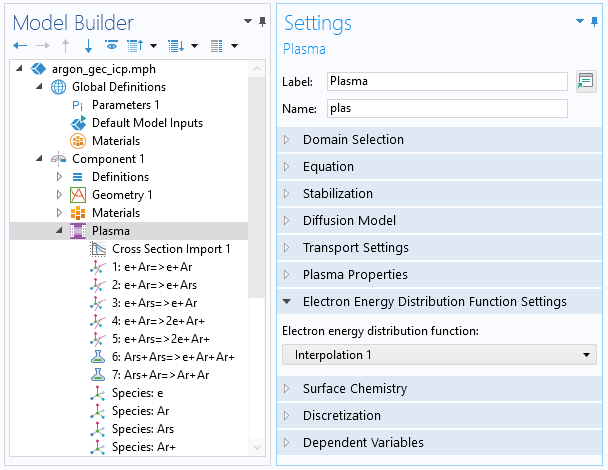
電子移動度や拡散係数などの輸送特性の関数も, 補間関数としてインポートできます. ただし, ここでは引数の数は1です. プラズマモデルノードでは, int2(plas.ebar) と入力することで, この補間関数を使用できます. この場合, int2 は関数の名前, plas はインターフェースのタグ, ebar は平均電子エネルギーです.


コメント (0)