Menu
COMSOL ブログ

熱粘性音響学の理論: 熱損失と粘性損失

Author Image
Mads Herring Jensen 著
2014年 2月 27日

音が小さな寸法の構造や形状を伝搬する場合, 熱損失と粘性損失により音波は減衰します. より具体的には, 損失は壁の近くの音響熱および粘性境界層で発生します. 正確なモデルを構築し, 実験測定と一致させるためには, この既知の現象を考慮して, これらの損失が熱粘性音響システムにどのように影響するかを評価する必要があります.

熱粘性音響学入門

コンデンサーマイク, MEMS マイク, 小型スピーカーなどの小型トランスデューサーの応答をモデル化する場合, 熱損失と粘性損失を含める必要があります. その他の用途には, 補聴器やモバイルデバイスのフィードバックの分析や, MEMS 構造の減衰振動の研究などがあります.

標準 IEC 60318-4 閉塞外耳道シミュレータ (711 カップラー とも呼ばれる) の伝達インピーダンスを分析することは, 熱電デバイスのシミュレーションを示す良い例であり, 下の図に示されています. 右側のグラフでは, 熱粘性音響損失がある場合とない場合の応答がモデル化されています. 曲線を標準データと比較するときに正しい動作を捕獲するには, これらのタイプの損失をシミュレーションに含める必要があることは明らかです.

圧力分布を示すプロット.

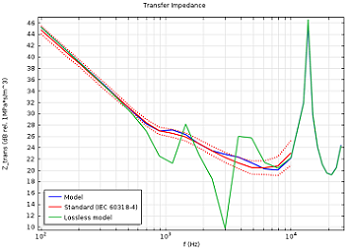
711 カップラーの伝達インピーダンスプロット.

IEC 60318-4 規格に準拠した, 7850 Hz での閉塞外耳道シミュレーター内の圧力分布 (左). 熱損失と粘性損失を含むカップラーのモデル化された伝達インピーダンスが青で表示され, 規定の標準曲線が赤で, 純粋なロスレスモデルから得られた曲線が緑で表示されます (右).

熱粘性効果は通常, 共振時に最も顕著になり, 共振を広げて周波数を下げます. これらの効果をモデル化するには, 熱伝導効果と粘性損失を支配方程式に明示的に含め, 運動量を ナビエ・ストークス方程式), 質量 (連続性), およびエネルギー保存方程式で解く必要があります. これは, 音響モジュールの 熱粘性音響 インターフェースで熱粘性音響方程式を解くことで実現されます. これらの方程式は, 粘熱音響または線形化ナビエ・ストークス方程式とも呼ばれます.

ここでは, 熱粘性音響方程式の物理的背景と, 重要な境界層特性である長さスケールについて説明します. また, 流体媒体を記述するために必要な材料パラメーターについても簡単に説明します.

熱粘性音響の背後にある物理学の探究

音響波は, 背景の定常 (大気圧) 圧力の上に圧力の小さな線形変動が伝播するものです. 変動の支配方程式 (波動方程式またはヘルムホルツ方程式) は, ナビエ・ストークス方程式, 運動量方程式, 連続方程式, エネルギー方程式などの流体力学の基本的な支配方程式を摂動, つまり 線形化することによって導き出されます. これにより, 小さな (音響) 摂動に対する運動量, 質量, エネルギーの保存方程式が得られます.

多くの音響シミュレーションアプリケーションでは, これらの方程式を簡略化するために一連の仮定が立てられます. システムは, 損失がなく, 等エントロピー (断熱かつ可逆) であると想定されています. ただし, 粘性効果と熱伝導効果の両方を保持すると, 圧力, 速度, 温度の音響摂動を解く熱粘性音響の方程式が得られます.

支配方程式の導出

周波数領域で支配方程式を導出する手順は, 安定した背景特性に関する小さな調和振動を想定することから始まります. 従属変数は, 次の形式になります

p = p_0+p'e^{i\omega t}, \quad \mathbf{u} = \mathbf{u}_0+\mathbf{u}' e^{i\omega t}, \quad T = T_0 + T' e^{i\omega t}

ここで, p は圧力, \mathbf{u} は速度場, T は温度, \omega は角周波数です.

プライム (‘) 付きの変数は音響変数であり, 下付き文字 0 が付いた変数は背景平均流量を表します.

熱粘性音響では, 背景流体は静止していると想定されるため, \mathbf{u}_0=\mathbf{0} となります. 背景圧力 p_0 と背景温度 T_0 を指定する必要があります (これらは空間の関数 T_0=T_0(\mathbf{x}) および p_0=p_0(\mathbf{x}) になります). 上記の式を支配方程式に挿入し, 1次変数で線形である項のみを保持すると, 粘性損失と熱損失を含む音波の伝播の支配方程式が得られます.

注: このプロセスの詳細については, 音響モジュールのユーザーガイド の熱粘性音響ブランチの理論的背景セクションを参照してください.

熱粘性音響 インターフェースの周波数領域における支配方程式は, 連続方程式 (すべての音響変数からプライムを省略) です

i\omega\rho =-\rho_0 (\nabla\cdot\mathbf{u})

ここで, \rho_0 は背景密度です. 運動量方程式

i\omega\rho_0 \mathbf{u} = \nabla\cdot \left(-p\mathbf{I}+\mu ( \nabla\mathbf{u}+(\nabla\mathbf{u})^T )+\left(\mu_\textrm{B}-\frac{2}{3}\mu \right)(\nabla\cdot\mathbf{u})\mathbf{I} \right)

ここで, \mu は動粘度, \mu_\textrm{B} はバルク粘度, 右側の項は応力テンソルの発散を表します. エネルギー保存方程式

i\omega (\rho_0 C_p T -\ T_0 \alpha_0 p) = -\nabla\cdot(-\textrm{k}\nabla T) + Q

ここで, C_p は定圧時の熱容量, \textrm{k} は熱伝導率, \alpha_0 は熱膨張係数 (等圧), Q は考えられる熱源です. 最後に, 圧力, 温度, 密度の変化を関連付ける線形化された状態方程式です

\rho = \rho_0 (\beta_T p -\alpha_0 T)

ここで, \beta_T は等温圧縮率です.

支配方程式の左辺は保存量, つまり質量, 運動量, エネルギー (実際はエントロピー) を表します. 周波数領域では, i\omega との乗算は時間に関する微分に相当します. 右辺の項は, それぞれの保存量を局所的に変更または修正するプロセスを表します. 方程式のうち2つには, 粘性せん断と熱伝導による拡散損失項があります. 粘性損失は速度場に勾配がある場合に発生し, 熱損失は温度に勾配がある場合に発生します.

粘性境界層と熱境界層

音波が壁で囲まれた流体内を伝播すると, 固体表面にいわゆる 粘性 境界層と 熱境界層 が形成されます. 壁では, 速度場には滑りなし条件, \mathbf{u} = 0, 温度には等温条件, T = 0 が適用されます. 等温条件は, 熱伝導が通常, 固体では流体よりも桁違いに高いため, 非常に良い近似です. これらの2つの条件により, 粘性境界層と熱境界層で構成される 音響境界層 が発生します. 流れは, ほぼ損失がなく等エントロピー (断熱) 条件で記述されるバルク条件から, この層内の条件に変換されます.

壁に沿って水平面で伝播する時間調和波 (パイプの小さな部分で伝播する波の場合もあります) の問題は, 以下の図に示されています. 左の図は速度振幅を示し, 右の図は壁からバルクに向かう流体の温度変化を示し, 中央の図は速度の大きさと, 調和周期にわたる速度ベクトルを示すアニメーションを示しています.

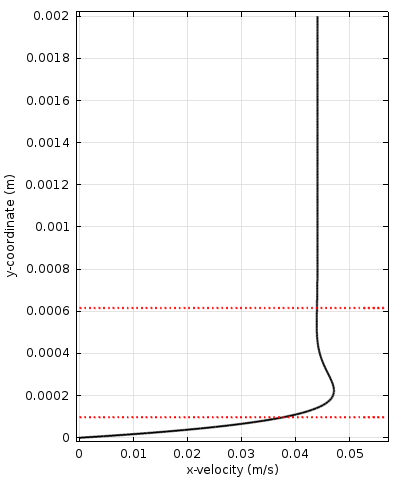
水平面で伝播する音響波の速度振幅.
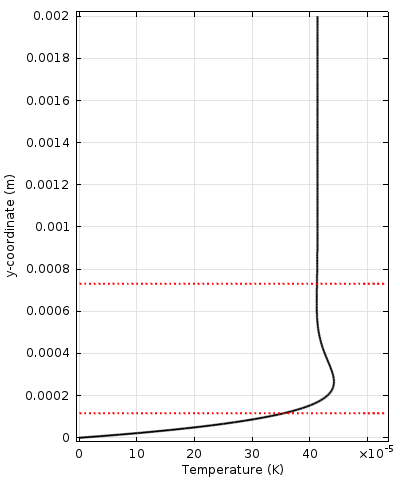
壁からバルクに向かう流体温度の変化.

 

水平面 (下) を伝播する音波の壁からバルクまでの速度振幅 (左) と流体温度 (右). 粘性境界層と熱境界層の厚さは, 壁に最も近い赤い点線で示されています. 上部の点線は, それぞれの場合で境界層の厚さの 2 \pi 倍を表しています. アニメーションは音響速度成分を示し, カラープロットは速度振幅を示しています.

粘性境界層と熱境界層がはっきりと見えます. 厚さは粘性浸透深さと熱浸透深さと呼ばれることもあります. 境界層では勾配が大きいため, ここでも損失が大きくなります. つまり, 比較的小さな寸法の系では, 境界層に関連する損失が重要になります. 多くのエンジニアリングアプリケーション (小型トランスデューサー, モバイルデバイスなど) では, 境界層に関連する損失を含めることが, 正しい物理的動作と応答をモデル化するために不可欠です.

粘性特性長さは, 上記の速度と温度のプロットで赤い点線で示され, その値の 2 \pi 倍 (粘性/熱波長と呼ばれる) も示されます. 2つの特性長さは, 無次元プラントル数 Pr によって関連付けられており,

\textrm{Pr} = \frac{C_p \mu}{\textrm{k}} \qquad \delta_\textrm{visc} = \sqrt{\textrm{Pr}} \: \delta_\textrm{therm}

これは, 系内の粘性損失と熱損失の比率の尺度となります. 空気の場合, この数値は 0.7 ですが, 水の場合は約 7.1 です. 空気では, 熱効果と粘性効果の重要性はほぼ同じですが, 水 (および他のほとんどの流体) では, 熱損失はより小さな役割しか果たしません. 粘性境界層と熱境界層の厚さは, 音響モジュールのポストプロセスで使用するための定義済み変数として存在し, ta.d_visc と ta.d_therm で表されます. プラントル数は ta.Pr で表されます.

平面波の問題は解析的に解くことができ, 粘性境界層の厚さ (d_\textrm{visc}) と熱境界層の厚さ (d_\textrm{therm}) の式をその後導出できます. これらは次のように与えられます

\delta_\textrm{visc} = \sqrt{\frac{2\mu}{\omega\rho_0}} \qquad \delta_\textrm{therm} = \sqrt{\frac{2 \textrm{k}}{\omega\rho_0 C_p}}

d_\textrm{visc} の値は, 100 Hz, 20 °C, 1 atm で空気の場合は 0.22 mm, 水の場合は 0.057 mm です. 以下の図は, さまざまな周波数における粘性境界層と熱境界層を示しています.

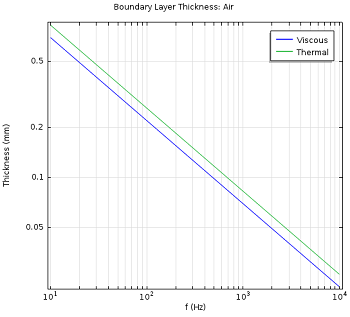
空気の粘性境界層と熱境界層の厚さの値を示すグラフ
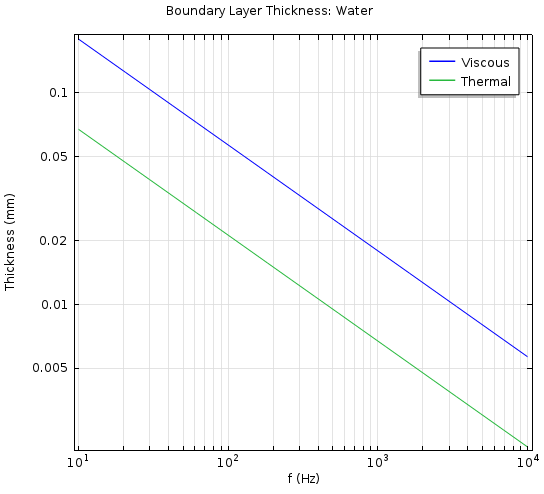
水の粘性境界層と熱境界層の厚さの値.

空気 (左) と水 (右) の周波数の関数としての粘性 (d_\textrm{visc}) および熱 (d_\textrm{therm}) 境界層の厚さの値.

これは, 音響波伝播周波数が増加すると, 粘性損失と熱損失の効果が減少することを示しています. 最後に, 熱粘性音響 インターフェースを使用してモデル化するときに捕獲されるもう1つの重要な効果は, 小型デバイスでの低周波数での断熱音響から等温音響への移行です. この効果は, 熱境界層がデバイス全体に広がるときに発生し, たとえば, B&K 4133 コンデンサーマイク などのコンデンサーマイクで重要です. 等温条件では, 音速が等温音速に変わります.

バルク損失, 減衰, および狭域音響

粘性損失と熱損失は流体のバルクにも存在することに注意することが重要です. これらは, 音響信号が長距離を伝搬して減衰するときに通常発生する損失です. その一例は, ソナー信号です. 空気中では, これらのタイプの損失は, 非常に高い周波数でのみ支配的です (オーディオ周波数では無視できます). もちろん, バルク損失は, すべての物理現象を含む熱粘性音響の支配方程式によっても説明されます. ただし, 熱粘性音響方程式を使用して大規模な領域をモデル化することは, 計算コストが非常に高くなります. 音響モジュールでは, 代わりに 圧力音響 インターフェースを使用し, 使用可能な流体モデル (粘性, 熱伝導, または 熱伝導および粘性) のいずれかを選択する必要があります.

熱粘性音響 インターフェースを使用したモデル化は, すべての物理的効果を捕獲するために必要な詳細のため, 計算コストが高くなる可能性があります. 音響波が一定断面の導波管またはダクト内を伝播する場合, 熱粘性損失は, 圧力音響 (周波数領域) インターフェースの 狭領域音響 機能を使用してモデル化できます. この領域機能は, 音響境界層に関連する損失を均質化された方法で流体に追加します. 損失は解析的に導出されるため, このケースでは正確です. この機能は, モデルサイズを縮小したり, 完全で詳細な熱粘性モデルに進む前に結果の最初の評価をすばやく取得したりするのに非常に便利です.

材料パラメーター

完全な熱粘性音響モデルを解くには, いくつかの材料パラメーターを定義する必要があります:

  • 動粘度, \mu
    • 動粘度 \mu は, 流体のせん断に対する抵抗を測定します. これは, 応力と速度勾配を関連付ける定数です. 動粘度は, 関係 \mu = \rho_0 \: \nu によって動粘度 \nu に関連付けられます. 動粘度の記号 \eta も使用されることがあります.
  • バルク粘度, \mu_\textrm{B}
    • バルク粘度は, 体積粘度, 第2粘度, または膨張粘度とも呼ばれます. これは, 流体の圧縮と膨張によって生じる損失に関係しています. \mu_\textrm{B} は応力テンソル項 (式 3 の右側) に現れ, バルク流体の圧縮率 (\nabla\cdot\mathbf{u}) に関係しています. この係数は測定が難しく, 周波数に依存することがよくあります.
  • 定圧熱容量 (比), C_p
    • この材料パラメーターは, 流体の温度 (定圧) を変更するのに必要なエネルギーの量を測定します.
  • 熱伝導係数, \textrm{k}
    • フーリエの熱伝導法則における温度勾配と熱流束の比例係数.
  • 熱膨張係数 (等圧), \alpha_0
    • これは流体の体積熱膨張であり, 温度が上昇したときに流体が膨張する能力を表します.
  • 等温圧縮率, \beta_T
    • 流体の状態方程式の重要なパラメーター. これは, 圧力の変化と流体の体積の変化を関連付けます. 等温圧縮率は, \beta_T = \gamma \beta_s による比熱比を介して, 通常の (等エントロピー) 圧縮率と関連付けられます.

熱粘性音響理論に関する結論

熱粘性音響の理論と関連する方程式について説明したので, COMSOL Multiphysics と音響モジュールを使用して熱粘性音響モデルを設定するためのヒントとコツに移ることができます. これと, 多くの例とアプリケーションについては, このシリーズの次のブログ で説明します.

その他の資料と参考文献

  • COMSOL ドキュメントの 音響モジュールユーザーガイド の熱粘性音響ブランチセクション
  • D. T. Blackstock, “Fundamentals of Physical Acoustics”, John Wiley and Sons, 2000
  • S. Temkin, “Elements of Acoustics”, Acoustical Society of America, 2001
  • B. Lautrup, “Physics of Continuous Matter”, Second Edition, CRC Press, 2011
  • P. M. Morse and K. U. Ingard, “Theoretical Acoustics”, Princeton University Press
  • A. D. Pierce, “Acoustics: An Introduction to Its Physical Principles and Applications”, Acoustical Society of America, 1989
  • A. S. Dukhin and P. J. Goetz, “Bulk viscosity and compressibility measurements using acoustic spectroscopy”, J. Chem. Phys. 130, 124519 (2009)

編集者注: このブログは, COMSOL Multiphysics バージョン 5.2a と一致するように 2016年7月12日に更新されました.

コメント (0)

コメントを残す
ログイン | 登録
Loading...
COMSOL ブログを探索
カテゴリー
タグ