前回のブログでは, 密度勾配理論 (文献 1) について簡単に紹介しました. この理論は, 過度の追加計算コストを必要とせずに, 従来のドリフト拡散定式化における量子閉じ込めの効果を考慮します. したがって, この理論は, 他のより洗練された量子力学的方法よりもはるかに迅速なエンジニアリング調査を可能にします. ここでは, 半導体デバイスの物理シミュレーションにおけるこのモデリング アプローチの利点を示す 3 つの例を引き続き示します.
例1: Si 反転層
金属酸化物シリコン (MOS) 構造は, 多くのシリコン平面デバイスの基本的な構成要素です. 酸化物シリコン界面の下の反転層は, さまざまな手法を使用して広範に研究されてきました. この最初の例では, Ref. 2 に基づく シリコン反転層 を, 従来のドリフト拡散定式化, 密度勾配理論, および完全に量子力学的な シュレーディンガー・ポアソン方程式 を使用してシミュレートします. ゲート酸化物の厚さは 3.1 nm, ドーピング濃度は 3.8e16 1/cm3 です. 密度勾配有効質量は電子質量の 1/3 です. 温度は 300 K で, フェルミ・ディラック統計が使用されます.
下のグラフに示すように, ドリフト拡散 (“DD”と表示) から得られる電子濃度分布には明らかに量子閉じ込めの効果が欠けており, 密度勾配 (“DG”と表示) から得られる電子濃度分布はシュレーディンガー・ポアソン方程式 (“SP”と表示) から得られる電子濃度分布に非常に近いです.
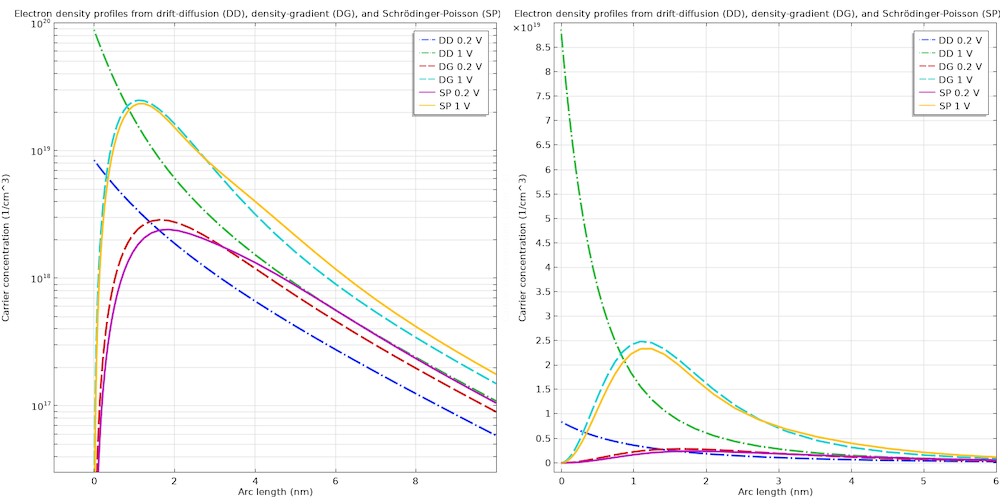
従来のドリフト拡散定式化 (DD), 密度勾配理論 (DG), シュレーディンガー・ポアソン方程式 (SP) による電子密度プロファイル. 左: 対数スケール, 右: 線形スケール.
密度勾配の結果は, 完全な量子力学的処理の結果と完全には一致しませんが, 従来のドリフト拡散定式化に比べて大幅に改善されています. さらに, シュレーディンガー・ポアソン方程式よりも計算リソースがはるかに少なくて済みます. この単純な 1D モデルでは, 密度勾配の計算時間は 6 秒で, シュレーディンガー・ポアソン方程式の計算時間は 253 秒です. 高次元のより複雑なモデルでは, この差はさらに大きくなります.
例 2: Si ナノワイヤー MOSFET
この シリコン ナノワイヤー MOSFET の 3D モデル は, 文献 3 に基づいています. シミュレートされた構造のチャネルは, 厚さ 0.8 nm の酸化層に囲まれた 3.2 nm の正方形断面を持つ長方形のシリコン ナノワイヤーによって形成されます. このチャネルの長さは 4 nm で, 温度は 300 K に保たれます. 参考文献でも, マクスウェル ・ボルツマン統計が一貫して使用されています.
このモデルでは, 密度勾配有効質量は異方性です. これは, 以下のスクリーンショットに示すように, 半導体材料モデルドメイン条件の設定ウィンドウの材料特性, 密度勾配セクションの対角線オプションを選択することで実現します.
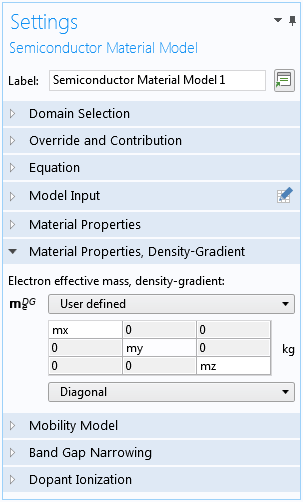
異方性有効質量行列の設定.
酸化物層は, 電荷保存ドメイン条件を使用して明示的にモデル化されます. シリコン酸化物界面の量子閉じ込め効果は, 下のスクリーンショットに示すように, 絶縁体界面境界条件のポテンシャル障壁オプションを選択することで組み込まれます. このオプションは, 文献 4で説明され, 前回の投稿で簡単に説明されている境界条件を実装します.
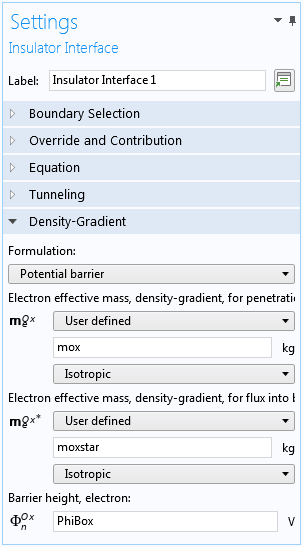
半導体と絶縁体の界面に量子閉じ込めを追加するための設定.
以下の図に示す I-V 曲線と電子密度プロファイルはすべて, 文献 3 の対応する図とよく一致しています.
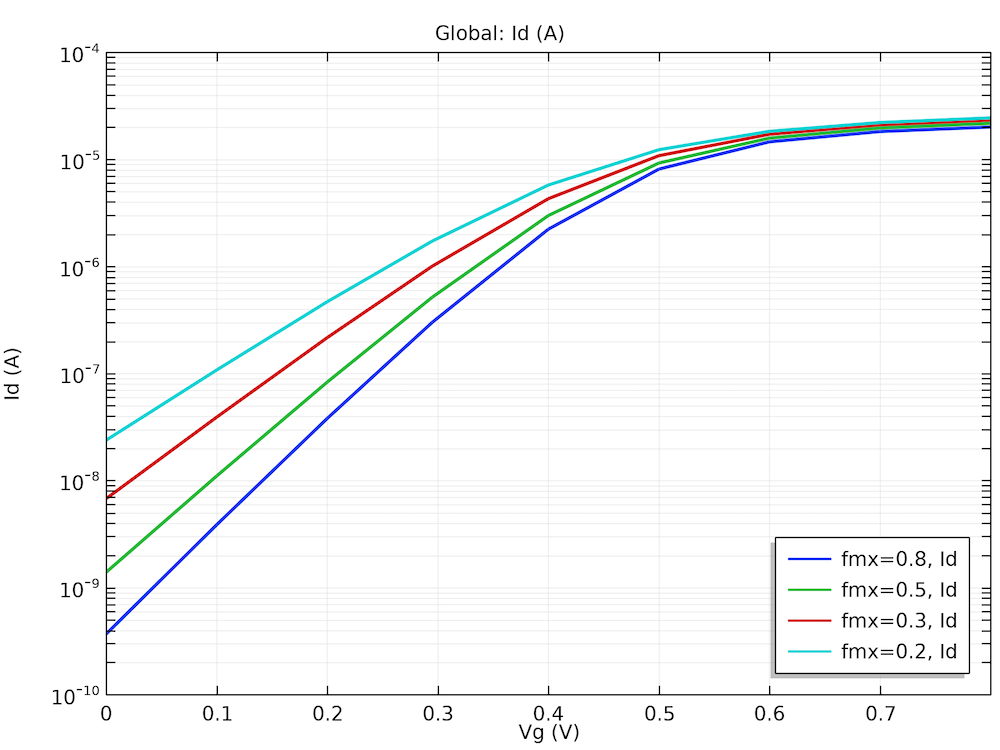
密度勾配縦方向有効質量のI-V曲線.
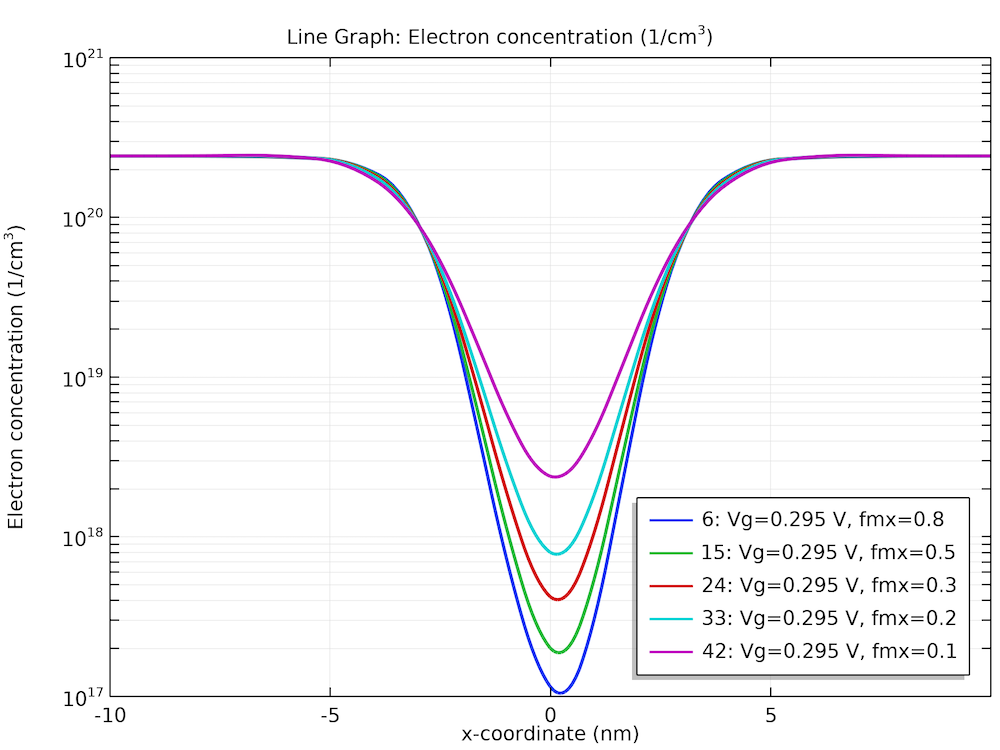
密度勾配縦方向有効質量セットの縦方向電子濃度プロファイル.
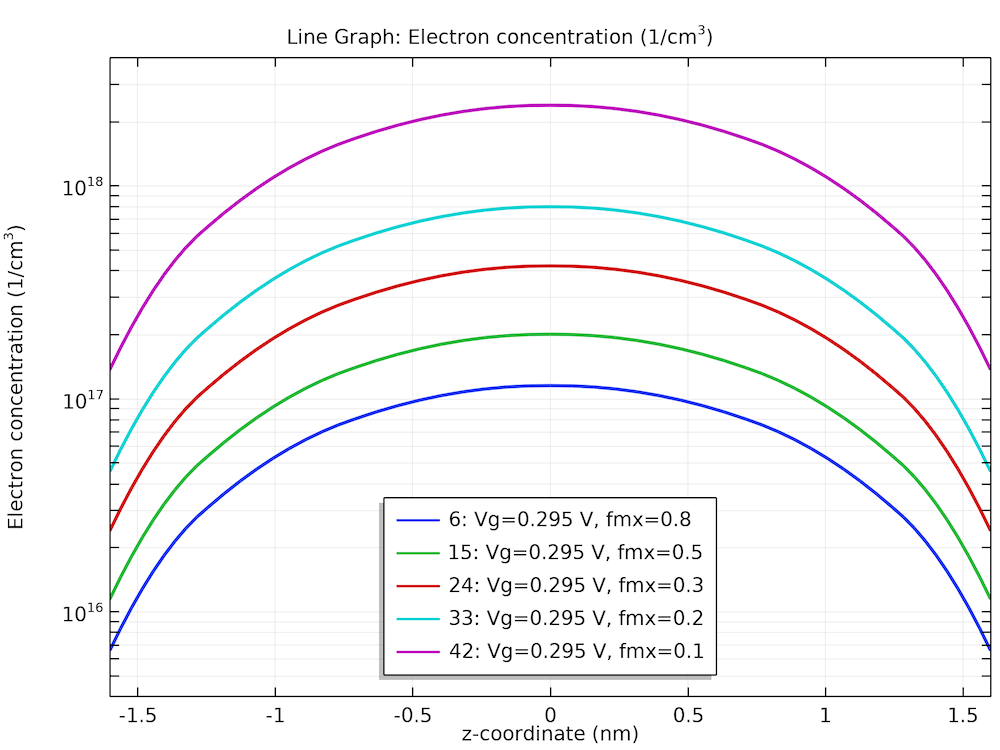
密度勾配縦方向有効質量セットの横方向電子濃度プロファイル.
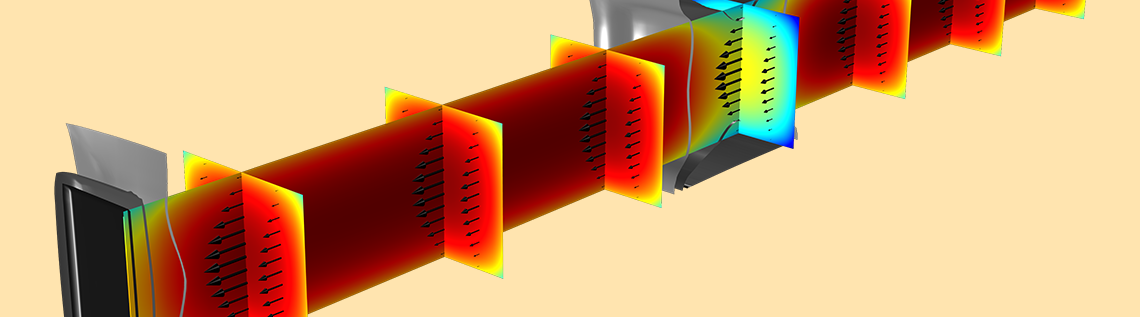
上記の最後のグラフでは, 酸化物とシリコンの界面における量子閉じ込めの効果が明らかです. 下のグラフは, 電子密度 (カラースライス), 電流密度 (黒矢印), および電位 (グレースケール等値面) の 3D 分布のスナップショットを示しています.
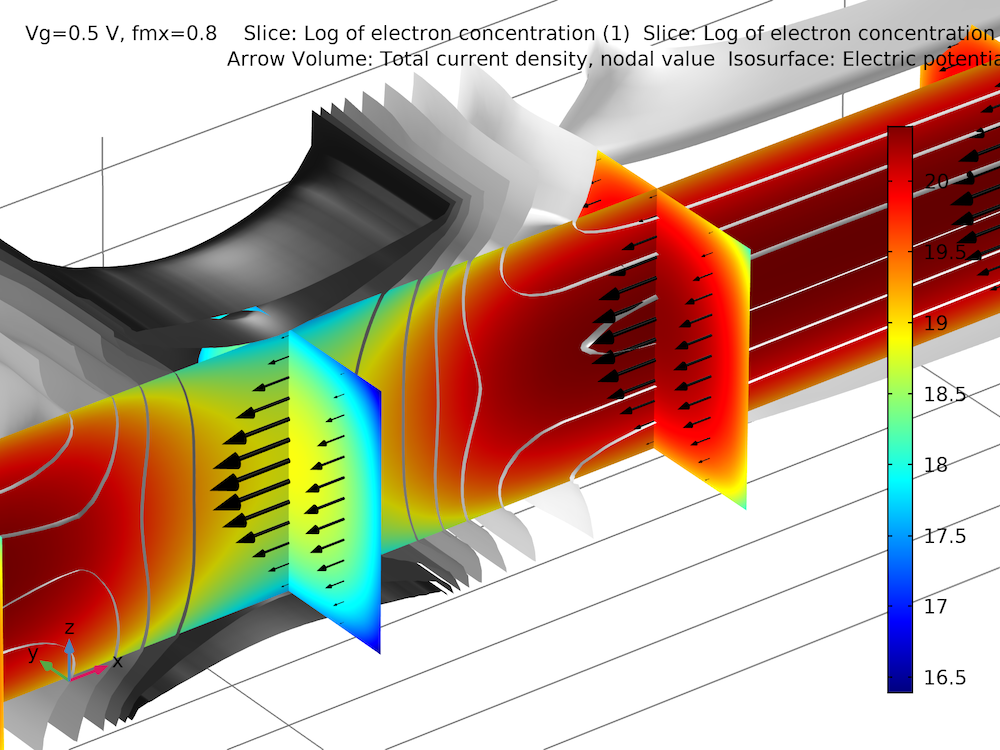
例3: InSb p-チャンネル FET
このモデルは, 文献 5 に基づいて, ナノメートルスケールのチャンネルを持つ InSb FET の DC 特性 を分析します. シミュレーションされた構造のチャネルは, AlInSb バリア材料の上に構築された 5 nm 厚の InSb 量子井戸層によって形成されます. 次に, 量子井戸層の上に 10 nm 厚のバリア層が追加され, その後にソースおよびドレインコンタクト用の p+ キャップが追加されます. 温度は 300 K で, フェルミ・ディラック統計が使用されます.
量子井戸層の量子閉じ込め効果は, 井戸バリア界面で有効になっている 連続/ヘテロ接合境界条件のデフォルトの 連続した疑フェルミ準位 オプションによって自動的に考慮されます. さらに, 前の例と同様に, 絶縁境界条件の ポテンシャル障壁 オプションを選択することで, 上部バリア層境界 (上部障壁と真空の界面) の量子閉じ込め効果が追加されます. 密度勾配有効質量は異方性であり, 前の例と同じように設定されます.
参照論文では, 場依存の移動度モデルが採用されています. 単純な形状であれば, 移動度モデルには電場の x 成分を使用すれば十分です. しかし, ここでは, 任意の形状に適用できるより一般的な手順を選択します. Caughey-Thomas 移動度モデル (E) サブノードが 半導体材料モデル ドメイン条件に追加され, 移動度モデルで使用される電場の平行成分が提供されます. ソルバーシーケンスは, 以下のスクリーンショットに示すように, 前の解 ノードを使用して電場の平行成分の更新を遅らせることで, 結果として得られる高度に結合したシステムの収束を達成するために調整されます.
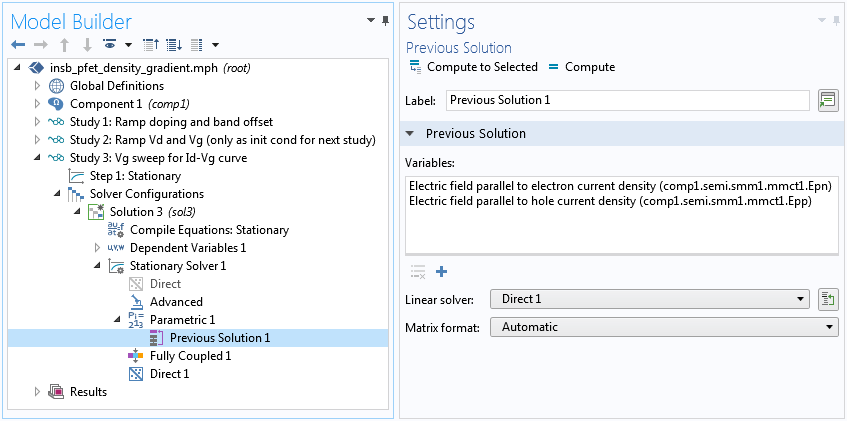
ソルバーシーケンスの前の解ノードを使用して, 電場の平行成分の更新を遅らせ, 任意のジオメトリの一般的なケースの収束を達成します.
次のグラフに示す I-V 曲線とホール密度プロファイルは, 文献 5 の図とほぼ一致しています.
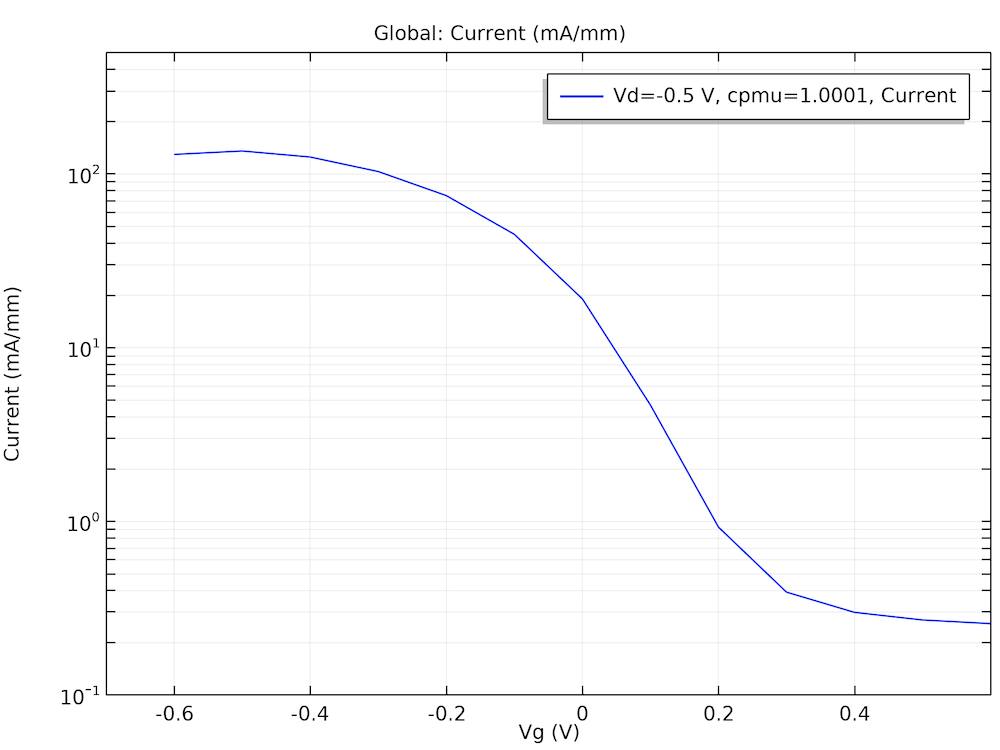
=” InSb FETモデルのI-V曲線.
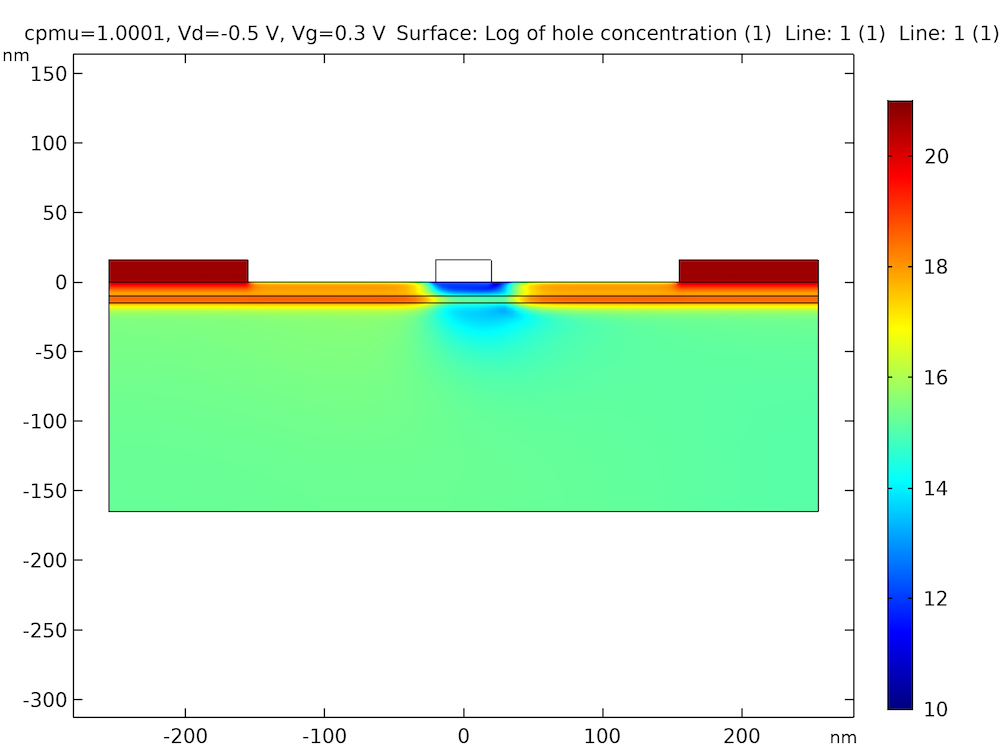
量子閉じ込め効果を示すホール濃度プロファイル.
下の図は, x = -100 nm でのホール密度プロファイルのラインカット (青い曲線) と近似ドリフト拡散プロファイル (赤い点線) を比較し, 量子井戸層と上部バリア真空界面 (y = 0 nm) の両方における量子閉じ込めの効果を定性的に示しています. 価電子帯端 (“Ev”) とホールの疑フェルミ準位 (“Efp”) もプロットされています. この比較は定性的なものにすぎないことに注意してください. これは, モデルが従来のドリフト拡散定式化を使用して再求解されていないためです. したがって, モデルが再求解され, 絶対値が再求解されなかった場合, 近似ドリフト拡散プロファイルの形状のみが結果を表します. それにもかかわらず, 量子閉じ込めの有無による処理の質的な違いは, ホール濃度プロファイルの形状の違いによってよく特徴付けられます. ヘテロ接合でのキャリアの蓄積がないこと, および上部のバリアと真空の界面からのキャリアの反発は, どちらも量子閉じ込め効果を明確に示しています.
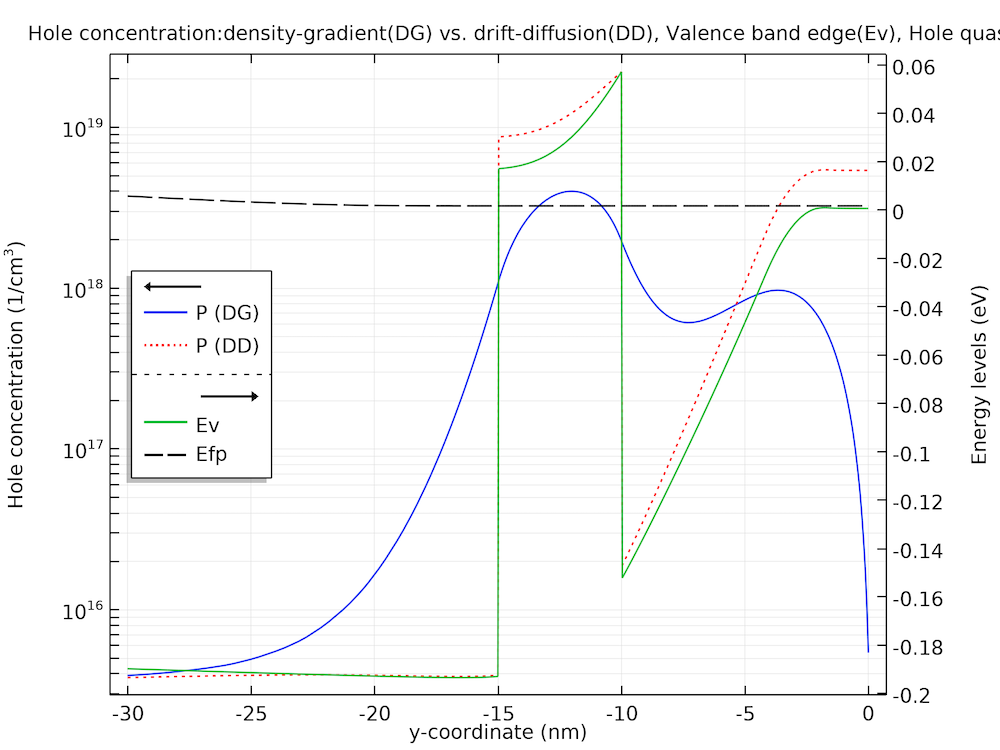
量子閉じ込め効果を解明するためのラインカットプロット.
半導体デバイスのモデリングに関する最終的なコメント
トランジスターの物理的サイズが縮小し続けるにつれて, 量子閉じ込めの影響はもはや無視できなくなりました. この影響をデバイス物理シミュレーションに含めるために, この 2 部構成のブログ シリーズでは, 計算効率の高い密度勾配理論といくつかのモデリング例を紹介しました.
次のステップ
このブログで紹介されているチュートリアルモデルをダウンロードしてください:
密度勾配定式化を実際に試すには, 下のボタンをクリックして評価ライセンスについてお問い合わせください.
参考文献
- M. G. Ancona, “Density-gradient theory: a macroscopic approach to quantum confinement and tunneling in semiconductor devices,” J. Comput. Electron., vol. 10, p. 65, 2011.
- M. G. Ancona, “Equations of State for Silicon Inversion Layers,” IEEE Trans. Elec. Dev., vol. 47, no. 7, p. 1449, 2000.
- A. R. Brown, A. Martinez, N. Seoane, and A. Asenov, “Comparison of Density Gradient and NEGF for 3D Simulation of a Nanowire MOSFET,” Proc. 2009 Spanish Conf. Elec. Dev., p. 140, Feb. 11-13, 2009.
- S. Jin, Y. J. Park, and H. S. Min, “Simulation of Quantum Effects in the Nano-scale Semiconductor Device”, J. Semicond. Tech. Sci., vol. 4, no. 1, p. 32, 2004.
- M. G. Ancona, B. R. Bennett, J. B. Boos, “Scaling projections for Sb-based p-channel FETs,” Solid-State Electronics, vol. 54, p. 1349, 2010.






コメント (0)