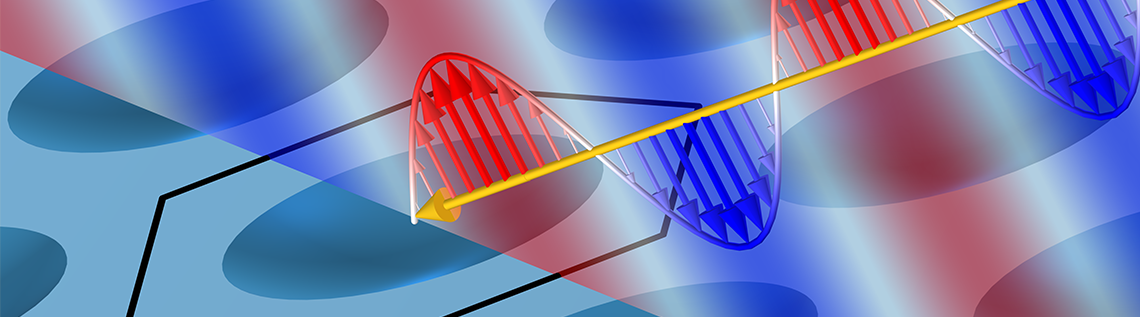
電磁放射の平面波, 例えば光, が平面周期構造に入射すると, 高次の回折が発生することがあります. これは, 光がスネルの法則に従って反射および屈折するだけでなく, 回折次数と呼ばれる複数の異なる方向に散乱する可能性があることを意味します. 幾何学的アプローチを使用すると, これらがいつ発生するか, どの方向に光が散乱するかを理解するのに役立ちます. 詳しく学びましょう.
平面周期構造からの回折を理解する
ここでは, 平面内で無限に周期的な構造に入射する光の平面波を考えます. 平面の上下の媒体は異なる屈折率を持つことができ, 損失がなく, 無限の広がりがあると想定します. これらの媒体間の界面には, 平面内で周期的に繰り返される限り, 材料特性と形状に関してあらゆる複雑さの周期構造が存在する可能性があります. このような構造に入射する光は, 少なくとも鏡面反射をします. 光は屈折(鏡面透過とも呼ばれます)も経験し, 電磁エネルギーが熱に変換されるときに損失が発生する場合もあります. 反射角と屈折角はスネルの法則によって与えられますが, 周期構造内で反射, 透過, または散逸する入射光の割合を計算するには数値解析が必要です.
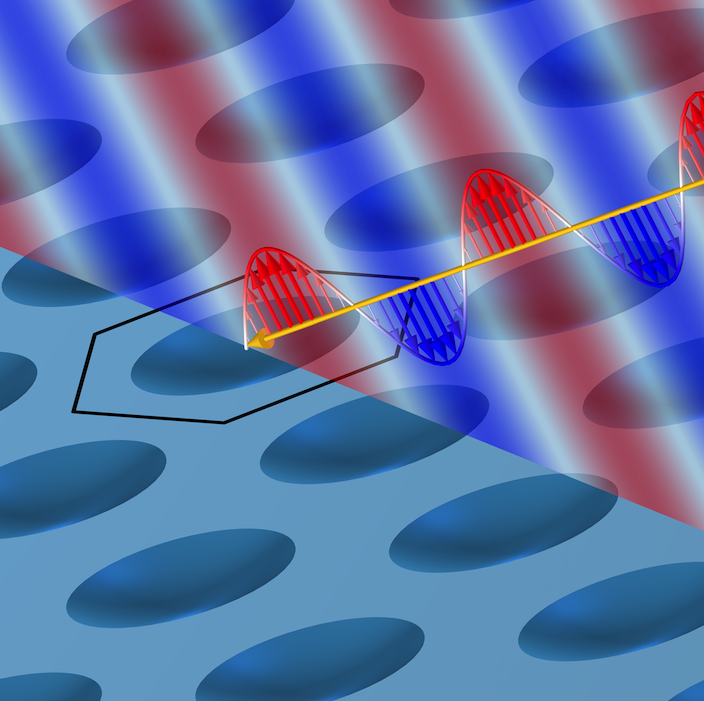
平面周期構造に斜めに入射する平面波. 周期構造の 1 つの単位セルが強調表示されます.
前述したように, 高次の回折の可能性もあります. これは, 周期構造によって散乱される光が別の方向に強めに干渉するときに発生します. このような結果のサンプルを以下に示します.
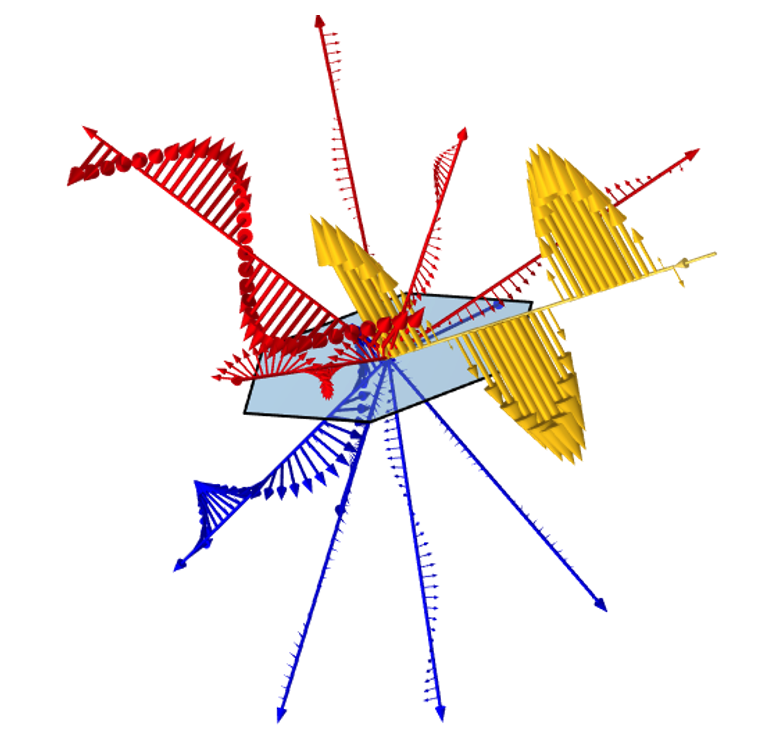
周期単位セルに入射する直線偏光の平面波 (黄色) の図. 入射光は, 反射 (赤) と透過 (青) で異なる強度と偏光を持ついくつかの異なる回折次数に散乱されます.
これら他の方向に向かう光の割合を決定するには, 同様に数値モデルを構築する必要がありますが, 光がどの方向に散乱するかを理解することは, エワルド球構造と呼ばれる純粋に幾何学的なアプローチで行うことができます. 数値解析を始める前にこのアプローチを理解しておくと役に立ちます. それをここで示します. エワルド球の幾何学的構造は, 平面内の 1 方向に周期性のある平面構造と 2 方向に周期性のある平面構造の両方に使用できます.
一方向周期性のある構造
格子などの一部の平面周期構造は, 一方向にのみ周期的変化を持ちます. これは, 3 次元に沿った構造に変化がないことを意味します. 入射光がこの 3 次元に垂直な平面内を伝播する場合, モデリングは 1 方向に沿った周期性を持つ 2 次元平面に縮小できます.
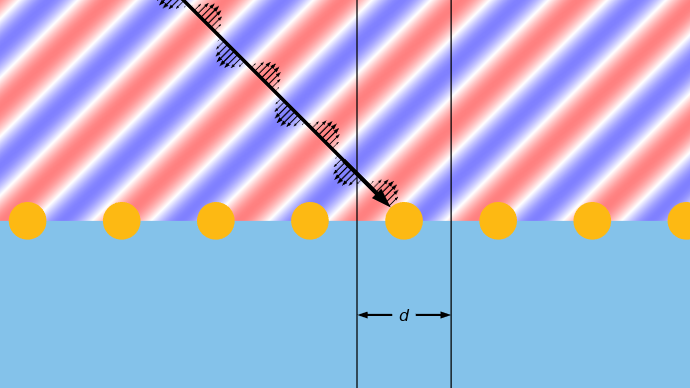
面外方向に沿って構造や場に変化がなく, 一方向に周期性を持って構造に斜めに入射する平面波. 1 つの単位セルが強調表示されます.
これらの構造では, 単位セルの間隔のみを考慮する必要があり, d, また, 逆空間に格子点の集合を描くことから始めます. 次の図は長さの逆の次元を持ちます. これらの格子点の線は, 周期構造の界面の平面に対応します. 格子点間の間隔は 2\pi/d で, 点は単位セルの中央に位置すると考えることができる0 番目の格子点, m=0, からインデックスが付けられます. 次に格子点の線の上下に半円を2つ描きます. これらの半径は反射側で n_{r}2\pi/\lambda_{0}, 透過側でn_{t}2\pi/\lambda_{0} です. ここで, n_{r} と n_{t} はそれぞれの側の屈折率, \lambda_{0} は自由空間の波長です. 法線から \theta_{inc} の角度で入射する入射光の場合, これらの円の共通中心は 0 番目の格子点から sin(\theta _{inc})n_{r}2\pi/\lambda _{0} だけオフセットされます. これらの半円内にある格子点は, 可能な回折次数に対応します.
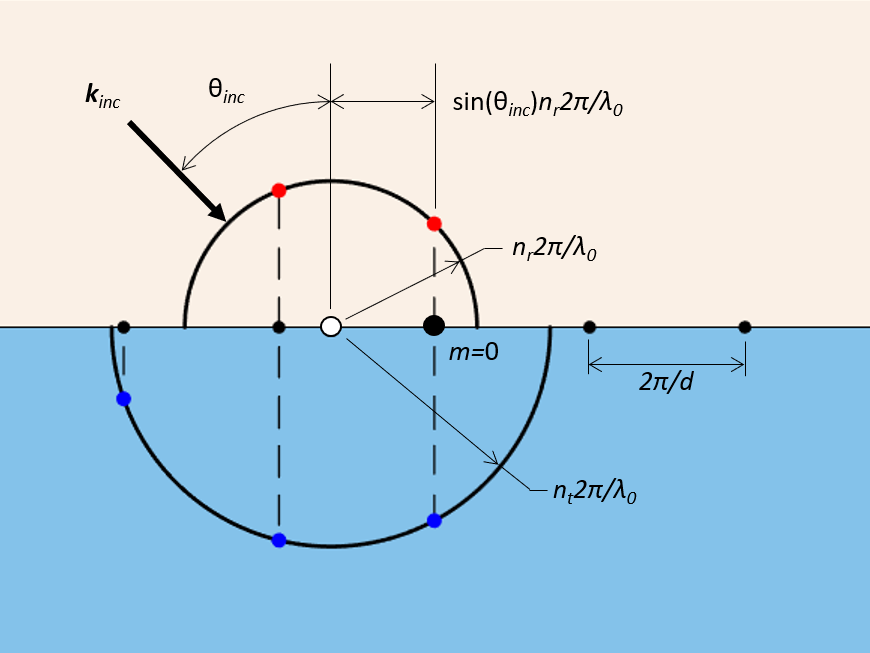
ある角度で入射する平面波によって照射される, 一方向に周期性のある平面構造から回折次数を決定するために使用される幾何学的構造. 半円 (白い点) の中心が 0 番目の格子点からどのようにオフセットされているかに注目してください.
この構造を使用して, 回折が発生する方向を決定し, それぞれにインデックスを割り当てることもできます. 半円の中心から格子点の投影までのベクトルは, 各回折次数の \textbf{k} ベクトルに対応します. これらの格子点のインデックスは両側で反対の符号になります. 0 次の格子点への矢印は常に存在します. それらは鏡面反射と透過を表します. 他の回折次数の存在は, 波長, 屈折率, 間隔, 入射角によって異なります. このタイプのモデルを設定する 2 つの例が, アプリケーションギャラリのエントリに示されています: RF モジュールによる プラズモニックワイヤーグレーティング (RF), および波動光学モジュールを使用するプラズモニックワイヤーグレーティング (波動光学).
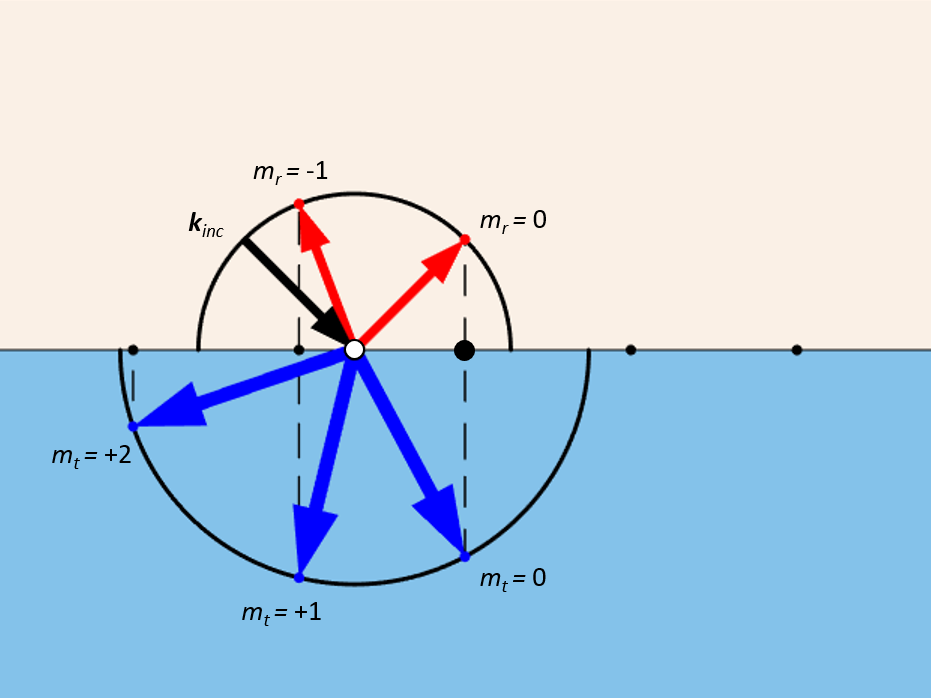
一方向に周期性のある平面構造からのさまざまな回折次数の波数ベクトル. 反射回折次数と透過回折次数の間のインデックスの符号の切り替えに注目してください.
2方向に周期性を持つ構造
次に, 面内の 2 方向に周期性を持つ平面構造からの回折の場合に移ります. 下の図は, 平面をパターン化する長方形, 菱形, 六角形の単位セルを示しています. これらは 2 つの単位セルベクトル, \textbf{a}_{1} と \textbf{a}_{2} によって定義されます. ある点から始まり, 隣接するエッジをたどって次の頂点まで続きます. 任意の座標と方向を自由に使用できますが, このブログの目的では, 常に \textbf{a}_{1} を使用することを選択します. ベクトルはグローバルデカルトx 軸に沿って配置され, 常に照明の方向から単位セルを見下ろします. また, \textbf{b}_{1} と \textbf{b}_{2} という 2 つの基底ベクトルもあります. 並べ方のパターンを生成するために単位セルを平面内でどのように移動する必要があるかを説明します. つまり, 平面全体をパターン化するには, m と n の任意の整数値に対して m\textbf{b}_{1}+n\textbf{b}_{2} によって単位セルをコピーする必要があります. これら 2 つのベクトルの外積の大きさは, 単位セルの面積を求めるために使用されます: A_{c} = ||\textbf{b}{1}\times\textbf{b}{2}||.

長方形, 菱形, 六角形の単位セルの 2 次元平面パターン. 単位セルベクトルはセルの 2 つのエッジに対応し, 基底ベクトルは平面をパターン化するためにセルをどのようにシフトする必要があるかを示します.
これらの基底ベクトルは, 2 つの逆空間回折ベクトルを定義するために使用されます: \textbf{d}_{1} = 2\pi(\textbf{b}_{2} \times \textbf{n})/A_{c} および \textbf{d}_{2} = 2\pi(\textbf{n} \times \textbf{b}_{1})/A_{c}. ここで, \textbf{n} = (\textbf{b}_{1} \times \textbf{b}_{2})/A_{c} は周期平面, つまり, +z 軸に対する法線ベクトルです. これらの回折ベクトルは基底ベクトルに垂直であり, 整数の和を取ることによって周期面内に回折格子を作成するために使用されます: \textbf{d}_{1} と \textbf{d}_{2} 方向の m と n のインデックスペアに対応する格子内の各点に対してm\textbf{d}_1+n\textbf{d}_2 となります. ユニットセルの透過側では, ポイントは同じ位置にありますが, インデックスが切り替わり, 反対の符号を持ちます.
これらの回折点を 3D 空間の周期面上で可視化し, その面の上下に材料の波数ベクトルに等しい半径の半球を追加できるようになりました. これらの半球によって, 反射と透過にどの回折次数が存在するかが分かります. 最初にこの球の中心を m = 0, n = 0 点に置き, 垂直入射光を表します.
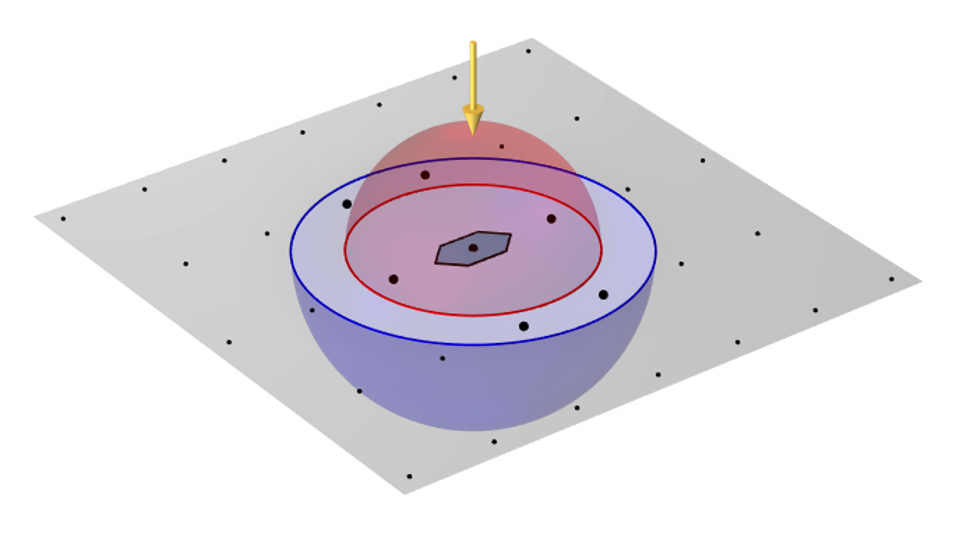
六角単位セル上に垂直入射する平面波光 (黄色の矢印). 回折点は周期面にプロットされ, 反射半球と透過半球内にある強調表示された点は, どの回折次数が存在するかを示します.
次に, 入射の仰角と方位角が変化すると何が起こるかを考えます. \textbf{a}_{1} ベクトルをグローバル +x 軸に揃えるという規則を選択していることに留意します. 入射の仰角を大きくすることは, 入射波ベクトルが最初に –y 軸を中心に回転することを意味します. 次に, 入射の方位角の増加により, +z 軸を中心として回転します. 従って, 入射の仰角は 0^{\circ} \le \alpha_{1} < 90^{\circ} から, そして, 入射の方位角は 0^{\circ} \le \alpha_{2} < 360^{\circ} から以下に示すようになります. 入射波数ベクトルは, 周期面の法線とともに入射面を定義します. 入射面は法線入射の場合, つまり, \alpha_{1} = 0^{\circ}, \alpha_{2 } = 0^{\circ} の場合, xz 面として定義されます.

入射の仰角と方位角は, 入射波ベクトル (黄色) の一連の連続回転を表します. 最初は –y 軸を中心に, 次に +z– 軸を中心に行われます. 入射面も表示されます.
入射角のこれらの変化により, 半球の中心の位置が変化します. 逆空間における半球中心から m = 0, n = 0 点までの距離は k_{r} = \text{sin(}\alpha_{1}\text{)}2π/ \lambda_r で, 位置は, 以下に示すように, 平面内で k_{x} = -k_{r}\text{cos(}\alpha_{2}\text{)} および k_{y} = -k_{r}\text{sin(}\alpha_{2}\text{)} だけシフトします. したがって, 仰角と方位角が変化すると, 異なる回折次数が現れることがよくあります.
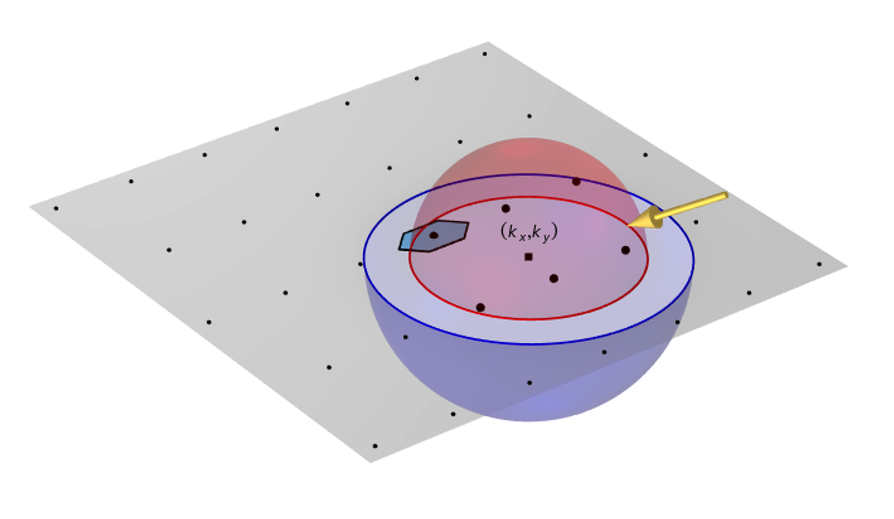
ゼロ以外の仰角および入射方位角で入射する平面波光に対しては, 半球の中心がシフトするため, 異なる回折次数が現れます.
これらの半球は, 各回折次数の波数ベクトルも示します. 回折次数点を半球に投影すると, 別の点のセットが得られ, 各回折次数の波数ベクトルは, 半球の中心からこれらの投影点までのベクトルに等しくなります.
回折点を半球に投影すると, 各回折次数の波数ベクトルが得られます. この幾何学的構造は, 入射光 (黄色) が反射 (赤) および透過 (青) の際にどの方向に回折されるかを示しています. この 3D モデルはマウスで操作できます. 左クリックで回転, 右クリックでパン, ホイールのスクロールでズームできます.
最後に, これらのベクトルは, 偏光状態がどのようになるかについても教えてくれます. 各回折次数について, 偏光状態は ジョーンズベクトル の面内成分と面外成分で表されます. 各回折次数の面は, 波数ベクトルと周期面の法線ベクトルによって記述される面です. ジョーンズベクトルの面外成分は, すべての回折次数について, 周期面に平行な電場を持つ波に対応します.
回折次数の方向は, 各回折次数の偏光状態を定義するために使用される平面の集合を記述します. 入射面と 1 つの回折次数が強調表示されます. この 3D モデルはマウスで操作できます. 左クリックで回転, 右クリックでパン, ホイールのスクロールでズームできます. .
おわりに
私たちは, 平面周期構造からの回折を理解するためにエワルド球を使用した幾何学的構築の結論に達しました. これにより, どの高次の回折次数が反射と透過に存在するかがわかります. また, ジョーンズ ベクトルの方向を定義するために使用される波数ベクトルと平面の集合もわかります. 数値モデルを解くときにこれらの情報はすべて自動的に取得されるため, この種の幾何学的構築を行う必要はありませんが, 理解と直感を構築するのに役立ちます.
他の参考資料
高次回折のモデリングを開始したい場合は, RF モジュールまたは波動光学モジュールを使用して構築できる次のモデル例が良い出発点となります.
- RF モジュールで作られたモデル:
- 波動光学モジュールで作られたモデル:






コメント (0)