最近, 電気に関する大きな誤解を解決しようとする面白いビデオがネット上で話題となり, 多くの論争が繰り広げられています. その誤解とは, 電気回路では電子がエネルギーを運んでいるというものです. この動画や多くの反響動画は確かに興味深いですが, この話にはさらに奥があります. そして, この理論を解析するのに最適なのが COMSOL Multiphysics® ソフトウェアなのです. では, 学んでいきましょう!
論争の背景
論争の元となったのは, 電気についての大きな誤解という動画です. 下図のような回路図が紹介されています. 理想的な電池が理想的なスイッチを介して接続され, 理想的な電源が形成されます. この電源は, それぞれ長さ30万キロメートルで, 反対方向に伸びる1体の抵抗ゼロのワイヤーに接続されています. これらのワイヤーは, 1メートル離れた電球にループ状に戻されています. 明示されてはいませんが, この回路全体は, 宇宙背景放射のない, ある種の空の宇宙にあり, この装置によって容易に検出されると仮定されています.
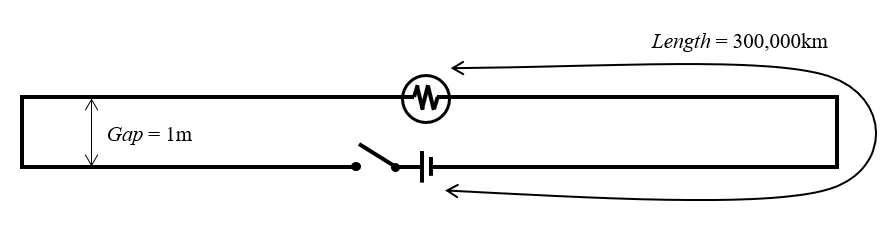
論争の元となった回路の図.
問題は, スイッチを閉じると, 信号が電源から電球に伝搬するのにかかる時間はどれくらいか, ということです. 答えは3.33ナノ秒 (ns) です. (Gap/c \approx 3.33\text{ ns}, ここで c は光速です). この頭の体操については, さまざまな方法で理解するための動画が出されています.
- “Energy Doesn’t Flow Inside Wires – Is Veritasium Right – RSD Academy“
- “Electric Energy Doesn’t Flow in Wires – Follow-up No. 2 – RSD Academy“
- “I bought 1000 meters of wire to settle a physics debate“
しかし, しきい値電流を定義し, どの値で電球が点灯するのかを調べる必要がある, という指摘もありました. COMSOL Multiphysics は, このような実用的な問題を得意としていますので, さっそく見ていきましょう!
数値モデルの構築と結果の把握
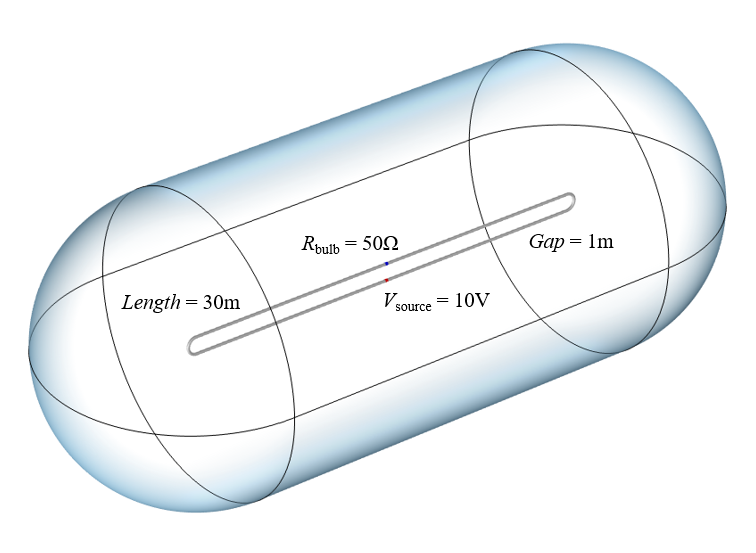
使用される計算モデルの図. ワイヤーの半径は0.1 m で, 計算領域の半径は10 m.
ワイヤーの周りの空間の電磁場を解くことになるので, 30万キロメートルの長さの計算モデルを構築するのは非現実的かもしれませんが, 上のような小さなモデルで多くのことを学ぶことができます. ソースのモデル化には, 時間ゼロから始まる均一な電位を印加する集中ポート機能を使用します. 電球は集中素子としてモデル化され, ワイヤーのもう一方の端のギャップに抵抗が加えられます. 長さ30 m の2本のワイヤーは, 完全導体の境界条件によってモデル化されます. このような超電導線はすでに作られているので, ワイヤーが完全導体であると仮定することは合理的です. ワイヤーの周りの空間は完全な真空とし, その境界は自由空間に開いているものとして扱われます. この計算モデルを構築すれば, ワイヤーにかかる電場と電流を解き, 可視化することができます.
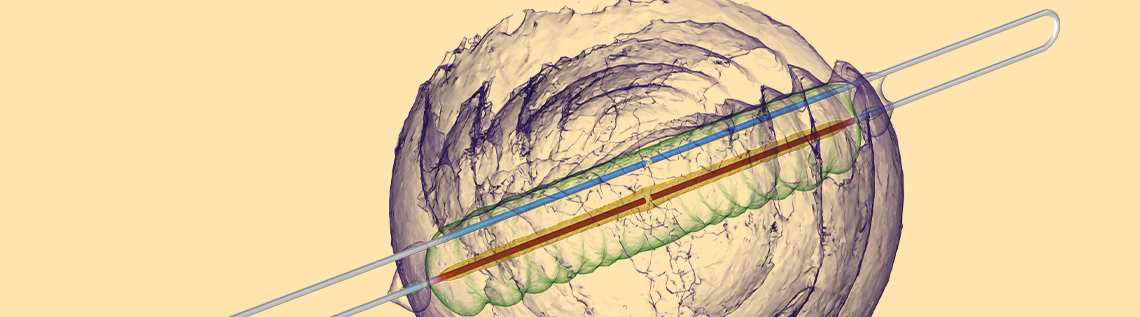
電磁エネルギー密度を半透明の等値面として表示した結果と, ワイヤーに沿った電流の様子. 信号の一部が光速で外部に伝搬し, ギャップを横切ってワイヤーに電流を誘導します. また, 電場はワイヤーに誘導され, 放射損失が発生します. より長い時間では, 系のインダクタンスと抵抗によって挙動が支配されます.
上のアニメーションは, 回路内とその周辺の電磁エネルギー密度を時間経過とともに示したものです. 初期信号が光速で外部に伝播し, 時間とともに変化する電場が電球の隣のワイヤーに到達すると, 電球に電流を誘導し始めることがわかります. 電場は主にワイヤーによって誘導されますが, 特に電場が屈曲部で反射される場合は, 多少離れて放射されます. 最初の数百ナノ秒後, 電場はどの瞬間でもより均一になり始めます. また, 電球に流れる電流を時間と共にプロットし, その形状が私たちの系について何を示しているかを議論することもできます.
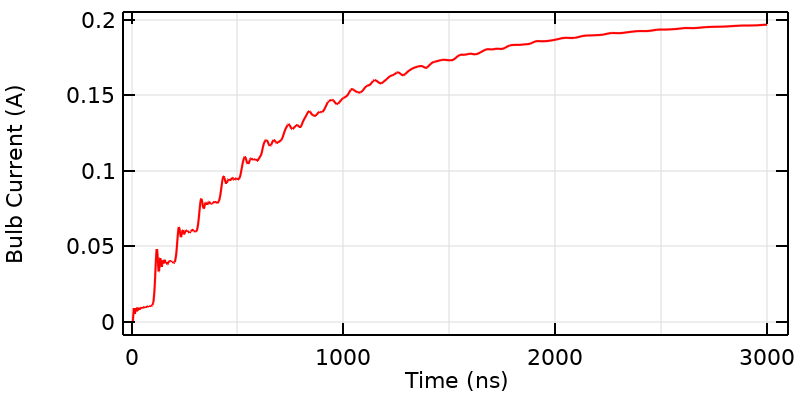
信号がギャップを伝搬するのに通常かかる時間よりも長い時間にわたって流れる電球電流. RL 回路の挙動と似ている.
全体形状
曲線の全体的な形状を見ると, 電球の電流が定常電流に向かって上昇しているように見えます. これは, この回路が RL 回路であるためで, 3.33 ns 後の全体的な形状を式で表すと I\left( t \right) = I_{DC}\left( 1 – exp(-t/\tau_{RL})\right) となります. ここで, RL の時定数は \tau_{RL} = L_{wires}/R_{bulb} であり, インダクタンス L_{wires} は定常状態モデルから計算することができます. 総インダクタンスはワイヤーの長さに正比例するため, ループが長いと立ち上がり時間が遅くなります.
電球が点灯するときのしきい値電流を I_{DC}=V_{battery}/R_{bulb} とすると, (厳密に数学的に考えると) 電流は限りなく I_{DC} に近づくだけで, 実際には電球が点灯することはありません. 実際には, 電球が測定するのは離散的な数の移動電荷の速度と加速度であるため, いずれは点灯するのですが. しかし, それでも DC 電流に非常に近いしきい値電流を設定すると, RL 時定数よりはるかに長い時間が経過するまで電球は点灯しないことになります.
明確なプラトー
開始時間付近の曲線をよく見ると, 信号にはいくつかの明確なプラトーがあり, 一種の階段状になっていることがわかります. これは, 印加されたステップ信号がワイヤー全体を伝わり, 各ワイヤーのちょうど中間地点にある屈曲部で反射が起こるためで, それぞれのプラトー部の特性時間は100 ns となります. これらのステップの高さは, ギャップ全体の容量性および誘導性カップリングに関係しています.
実際, 送電線の回路モデルでこの階段状の挙動を特徴づけることができます. これらのプラトーは時間とともに滑らかになることに注目してください. この滑らかさがどこから来るのかについては, すぐに説明します. その前にまず, 2番目の可能性について説明します. どのようなしきい値電流を指定するかによって, 電球は100 ns の整数倍で点灯する場合があるということです.
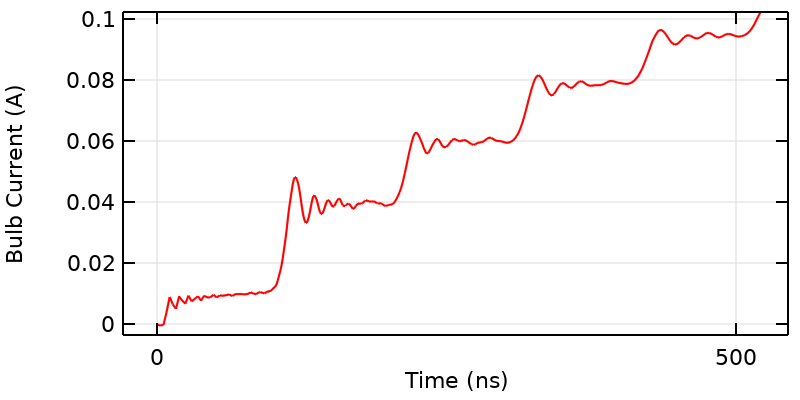
初期時間付近では, 時間の経過に伴う電流にも, 信号がワイヤーの全長にわたって伝搬する時間に等しい周期で, はっきりとしたプラトーが見られます. さらに, 理想化されたスイッチからのステップ変化と, 系の共振動作によって生じる振動があります. これらは系の損失により時間とともに減衰します.
速い波紋とその減衰
各ステップの開始点をさらに詳しく見てみると, 各ステップの開始点で高いピークを持った電流には波紋がはっきりと現れ, 次第に消えていくのがわかります. つまり, 適切なしきい値電流を選べば, 電球はまず点滅し, 次に点灯するという, 第3の可能性が見えてくるのです.
これらの波紋は, 系の空間的に分散されたキャパシタンスとインダクタンスによるもので, 1つだけでなく無限の共振が発生することになります. 私たちは, 系の高次の共振モードがソースによって励起されるのを観察しているのです. しかし, これらの波紋は減衰しているように見えることに注目してください. この減衰と信号の平滑化は, 損失によるものです. 損失の原因の1つは, 電池に蓄えられたエネルギーを熱と光に変換する既知の電球の抵抗です. 2つ目の損失の原因は, 回路の他の部分からのエネルギーの放射によるものです. この損失を正しく予測するには, ここで構築しているような3D のモデルが必要です.
高周波で波長の短いものは, 低周波の成分よりも早く放射されます. 別の言い方をすれば, 共振が高いほど品質係数が低くなる, またはワイヤーが一種の損失性ローパスフィルターであるということです.
また, これらの共振を励起するこの高周波成分が, どのようにモデルに導入されているのかも問わなければなりません. スイッチを閉じたとき, 印加される電位が段階的に変化することを思い出してください. このステップ変化には, どのような周波数が含まれているのでしょうか. この疑問は, フーリエ変換をすることで解決できます. 実は, 入力信号には無限の周波数が含まれているのです. 非常に高い周波数成分は大きさが小さく, すぐに放射されてしまいますが, これは現実的です. また, この周波数成分は, 回路とその設計について何かを教えてくれます. もし, ワイヤーの途中の曲げ部の形状を変えると, 異なる反射信号が得られるでしょう.
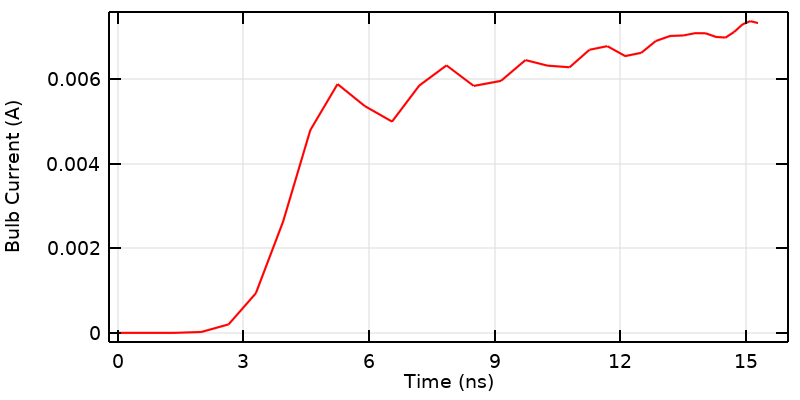
開始時間付近の結果を見ると, 数値計算方法は, 理想化されたスイッチの結果として, 若干の人工的な分散をモデルに追加しています. これは, 代わりに入力信号に現実的なランピングを追加することで対処できます.
開始時間付近の解
この曲線の最後の部分には, 特別に注目すべきものがあります. シミュレーションの最初の段階では, 信号は最初はゼロですが, 3.33 ns 前にゼロでなくなっていることがわかります. これは, 非物理的な状況, つまり瞬時にオンになるスイッチをモデル化しているために生じる小さな数値上のアーティファクトです. このようなスイッチは物理的に不可能です. 既知の最速の物理プロセスでさえ, 立ち上がりに1アト秒ほどかかります. もし, 結果のこの部分にこだわるのであれば, ステップ変化を現実的な立ち上がり時間を持つ過渡信号で置き換えることができます. また, 曲線をより滑らかにするために, 数値モデルを細かい時間ステップと細かい空間離散化で解く必要があります (これには長い時間がかかるでしょう).
この最後の点については, 基礎となる数値計算の手法が, 私たちが入れ忘れた分散を追加してくれている, という考え方もできます. これは数値解析の専門家レベルの話であり, 現実には情報が光速より速く伝わることはない, と言ってよいでしょう.
この論争に対する結論は?
簡単に言うと, そもそも論争の必要はないのです. 元のビデオから得られる正しい結論は, 検討中の回路では, 信号がソースから電球に伝搬するのに3.33 ns かかるということです.
より完全な捉え方をすれば, 応答曲線が以下の挙動を示すと言うことです.
- 電磁場がソースと電球の間の空間を伝搬するのにかかる時間の結果である遅延. その後, いくつかの電流が誘導される.
- RL 回路の応答. これは本質的に, 抵抗器と直列に接続された非常に大きな誘導性ワイヤーのループであるため.
- ワイヤーの中点での鋭い曲げでの信号の反射の結果として生じる段状のプラトー. これらのステップの高さは, 近接する平行線間の誘導性および容量性カップリングに支配される.
- 入力信号のステップ変化の結果として発生する高速の波紋が構造の共振を励起する.
- 電球の抵抗と放射の両方による高周波成分の減衰.
COMSOL Multiphysics を使用すると, このようなモデルを素早く構築し, 挙動を検証することができます. その他, 解析できる変更点をいくつか紹介します.
- ワイヤーの半径の変更. これにより, 容量性カップリングの大きさが変わり, ステップの高さや波紋の周期が変化する.
- 有限の導電率を持つワイヤーを検討する. この場合, 定常状態での電流は減少するが, 3.33 ns 直後の信号にはかなり小さな影響しか与えない. したがって, しきい値によっては, 3.33ナノ秒に電球が点灯し, しばらくして消灯することもあり得る.
- 2本のワイヤーの向きを変えて, 反対方向に進まないように近接させる. この場合, 多少のクロストークは発生するが, ワイヤーは伝送路に近い形で動作する.
他にどのようにこの回路を変更すれば, 異なる挙動が見られるでしょうか? 意見, 感想をお寄せください!
COMSOL Multiphysics® ユーザーのための補遺
上記の図を生成するのに使用したモデルをダウンロードして, 他の状況を試してみたい方は, 以下のリンクから入手できます. このモデルは, RF モジュールを使用して構築されています. また, この種のモデリングに有用な他のリソースも多数あります.
- DC の場合の電圧とアースに関するいくつかの基本的な概念を学ぶには, 電圧と接地は存在するのか? を読んでください.
- この系の伝送路の解釈について詳しく理解するためには 波動様の電磁場をモデリングする際の電圧と接地 を読んでください.
- 集中ポートと集中素子の励起を理解するには TEMおよび擬TEM伝送線 を参照してください.
- この例の信号が t = 3.33 ns の前に非ゼロに見える理由を理解するためには, 問題を空間と時間に離散化する有限要素法について理解しておくと便利です.
- より現実的なスイッチのモデル化方法については, 以下のナレッジベースのエントリーをご覧ください.
- 同様のモデリング技術をより現実的なデバイスに適用した例として, 時間, ドメイン反射率測定法のモデル例を参照してください.
- 有限導電率による表皮効果がどのように作用するか, また, これを考慮するために計算モデルをどのように調整する必要があるかを理解するには, 波動電磁気問題のモデリング を参照してください.
- 平行線伝送路の挙動を予測するには, こちらのアプリケーションギャラリのエントリを参照してください.
- もし, ノイズのない無限の宇宙を仮定することに抵抗がある場合は, 代わりに, 無響室の中にこの系を置いてモデル化することができます. このモデルについては, こちらのアプリケーションギャラリのエントリを参照してください.
- 伝送路に不均一な半径のワイヤーがあるとどうなるのか気になる方は, 波型導波路のインピーダンス計算 を読んでください.
- 我々のモデルがなぜワイヤーの周りにこれほど大きな空間の領域を含むのか疑問に思われる方は, 波動電磁場問題のための PML と散乱境界条件 を読んでください.
- このモデルのすべての場が中心に対して対称であることに気づいている方, また, これによってモデルを単純化できると考えている方は, まさにその通りです. 詳しくは, 磁場モデリングを簡素化する対称性を読んでください.
- 最後に, 電磁気学についての私のお気に入りの頭の体操の1つを知りたい方は 直線ワイヤーのインダクタンス計算 を参照してください.






コメント (0)