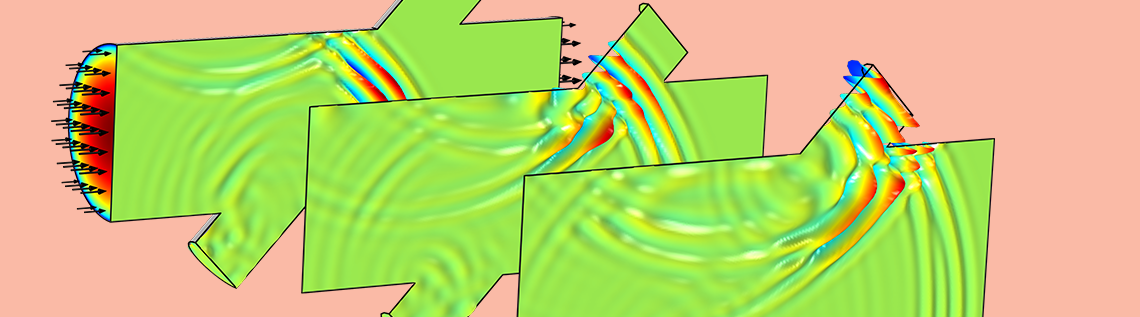
音響的に大規模な問題をモデル化するには, 不連続ガラーキン法のようなメモリ効率の高いアプローチが必要です. こうした問題を容易に解くために, この手法に基づいた新しいフィジックスインターフェース 対流波動方程式 (陽的時間発展) を音響モジュールに追加しました. このインターフェースは定常背景流を考慮でき, 線形超音波アプリケーションのモデリングに適しています. 本日は, 超音波流量計を例に, このインターフェースの使い方を説明します.
対流波動方程式 (陽的時間発展) フィジックスインターフェースについて
新しい 対流波動方程式 (陽的時間発展) インターフェースは, 音響モジュールの機能を基盤としています. このインターフェースの基盤となる技術は, 不連続ガラーキン法 (DG 法, 別名 DG-FEM) に由来しています. この法は, 時間陽解法でメモリ消費量が非常に少ないソルバーを採用しています. 対流波動方程式 (陽的時間発展) インターフェースを使用すると, 定常背景流中に多数の波長を含む大規模な過渡線形音響問題を効率的に解くことができます. また, 効果的な無反射境界条件として機能する吸収層 (スポンジ層) も備えています.
対流波動方程式 (時間陽的) インターフェースを用いた超音波流量計のモデル. 流量計を通過する背景流を計算するための乱流モデルも用意されています.
計算領域を切り捨てる吸収層技術とメモリ効率の高い DG-FEM 定式化により, 時間領域 (分解可能な波長数で測定) で非常に大規模な問題を設定し, 解くことができます. これにより, 対流波動方程式 (時間陽的) インターフェースは, 波長に対して長距離にわたる線形音響信号の伝播をモデル化するのに適しています.
このインターフェースは, 超音波流量計や超音波センサーなど, 飛行時間パラメーターが考慮される線形超音波アプリケーションに役立ちます. また, 室内音響や自動車キャビンなど, 過渡的な音響パルス伝播を経験する非超音波アプリケーションにも役立ちます.
線形化オイラー方程式の解法
対流波動方程式 (陽的時間発展) インターフェースで解く支配方程式は, 線形化オイラー方程式です. これらの方程式は, 断熱状態方程式を仮定しています (文献 1 および 文献 2 を参照). 質量保存方程式と運動量保存方程式は次のように表されます.
& \frac{\partial \rho}{\partial t}+\nabla\cdot(\rho \mathbf{u}_0 + \rho_0 \mathbf{u})=0 \\
& \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}_0\cdot\nabla)\mathbf{u} + (\mathbf{u}\cdot\nabla)\mathbf{u}_0 + \frac{1}{\rho_0}\nabla p -\frac{\rho}{\rho_0^2}\nabla p_0 = 0 \\
& p=c_0^2 \rho
\end{align}
音圧 p と音速摂動 u は従属変数です. 音速は c0 であり, 定常平均背景流変数は, 密度 ρ0, 圧力 p0, 速度場 u0 を介して添え字0で定義されます.
背景流は, 小さいものから中程度の速度勾配を持つ定常流です. 背景速度をゼロに設定すると, 方程式は実質的に古典波動方程式のモデル化に簡約されます. 界面には物理的な損失メカニズムはなく, 上記の方程式は保存型で設定されていることに注意してください.
陽的時間発展法による効率性の向上
対流波動方程式 (陽的時間発展) インターフェースは, 前述の通り, メモリ効率に優れた陽解法定式化である DG 法に基づいています. この手法では, 時間を進める際に系全体の行列を逆行列化する必要がなくなります. 一方, 陰解法ではこの行列の逆行列化が必要となり, 大規模な問題を解く際に大量のメモリを消費します. DG-FEM では, 時間発展させる前に, 参照メッシュ要素のいくつかの質量行列のみを逆行列化します (サイズを小さくするため). この手法は求積法を必要としません. DG 法に関しては, 局所流束ベクトルと流束の発散を計算するのは時間のかかるプロセスですが, BLAS レベル 3 演算 を使用すると効率的に実行できます.
RAM に収まる小規模から中規模の問題では, 陰解法の方が高速だと考えられることがあります. しかし, これは必ずしも真実ではありません. 比較する際には, 誤差レベルを確認することが重要です. 陰解法を使用すると, 時間ステップが大きすぎると, 時間法による誤差が生じてしまいます. 一方, 不連続要素のため, 同じ多項式次数とメッシュでは, DG 法の方が精度が高くなります.
圧力音響 (過渡) や 線形化ナビエ・ストークス (過渡) などの FEM ベースのフィジックスインターフェースでは, 時間陰解法を使用する必要があります. 課題は, モデルサイズや周波数が増加すると, 陰解法の RAM 消費量が急激に増加することです. 後者は, システム内の最小波長を一定数のメッシュ要素で解く必要があるためです. それでも, FEM 法はより柔軟性が高く, マルチフィジックスアプリケーションで容易に連成できます.
デフォルトの定式化では, 対流波動方程式 (陽的時間発展) インターフェースは4次形状関数を使用します. これは, DG 法で波動問題を解く際に速度と効率の面で最適な方法です. これにより, 解く必要のある最高周波数成分の波長の約半分の要素サイズのメッシュを使用できます. これにより, 大規模な問題のメッシュ生成が簡素化されます.
例えば, 以下に示す超音波流量計モデルは760万自由度 (DOF) で構成されており, 9.5 GB の RAM を搭載したデスクトップコンピューターで解くことができます. 陰的定式化では, このサイズのモデルをデスクトップで解くことは考えられません. コードは完全に並列化されて実行されるため, 解の計算時間は使用可能な RAM よりも, プロセッサーの速度とコア数に大きく依存します. DG-FEM 定式化は並列化に非常に適しています.
COMSOL は, 音響モジュールにおいて, DG-FEM 定式化が大規模波動伝播問題の解析に非常に効果的であると考えているため, 今後この定式化をさらに活用していく予定です. また, この手法とソルバーの改良と微調整にも継続的に取り組んでいます.
吸収層機能
前述のように, 対流波動方程式 (陽的時間発展) インターフェースには, 吸収層 機能が搭載されています. これは, 多くの周波数領域インターフェースに既に存在する完全整合層 (PML) に似たスポンジ層の一種です. 吸収層との違いは, スケーリングシステム, フィルタリング, そして単純な低反射インピーダンス条件を組み合わせた手法にあります.
層領域内では, 座標スケーリングによって伝播する波の速度が効果的に低下し, 波が外側の境界に向かって “上向き” (法線方向) に揃うようになります. つまり, 波は外側の境界に法線に近い方向から衝突することになります. フィルタリングは, スケーリングによって生成される波の高周波成分が減衰, 除去されます. 層の外側の境界では, 法線入射が確保されているため, 単純な平面波インピーダンス条件によって残りの波がすべて除去されます. 以下のアニメーションは, 2D一様流におけるガウスパルス: 対流波動方程式と吸収層 ベンチマークチュートリアルを使用して作成されたもので, 吸収層の動作を示しています.
一様背景流におけるガウス波の時間発展. 流れはマッハ 0.5 で右側に向かって移動します. 吸収層は出射波を吸収します.
COMSOL Multiphysics® における線形超音波アプリケーションのモデリング
対流波動方程式 (陽的時間発展) インターフェースの応用例として, 一般的な湿式飛行時間構成の超音波流量計を見てみましょう. 湿式超音波流量計には超音波信号用の専用信号管があり, 装置全体が流量測定が行われる管内に取り付けられます. 主流の速度を推定するために, 上流と下流を同時に通過する2つの信号の到達時間差を計算します.
このモデルでは, 流量計に水が満たされ, 主流路の直径は 5 mm です. 下の図は, 1つの対称条件を使用した場合の背景流れ場を示しています. 主流路の平均速度は 10 m/s です. (流れのシミュレーションには CFD モジュールが必要です. ) 信号管は, 主流路に対して 45° の角度で設置された小さな側管です.
このモデルの詳細については, アプリケーションライブラリ でステップバイステップの説明をご覧ください.
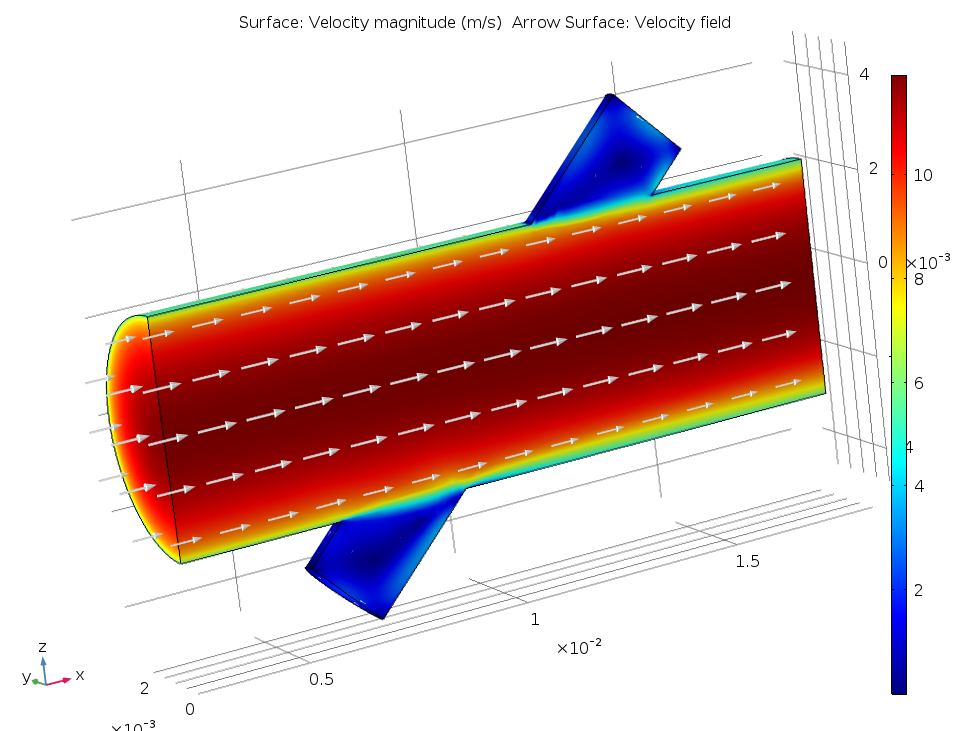
超音波流量計内部の背景平均流量.
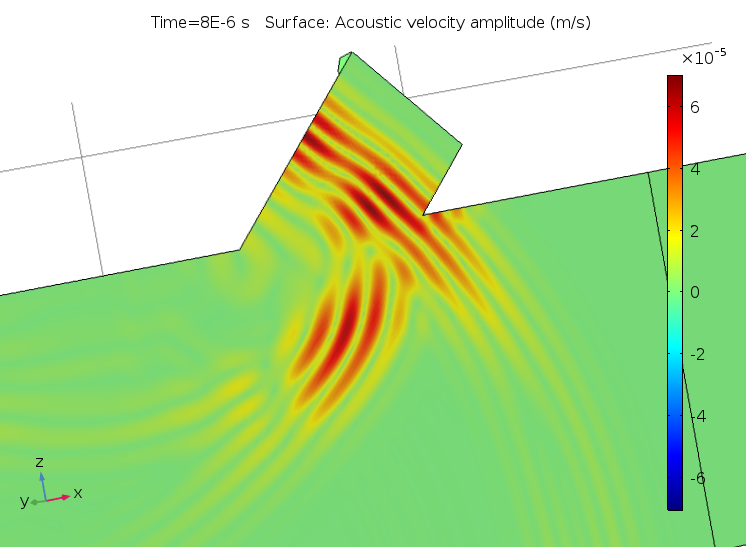
下のアニメーションは, 音響パルスが信号管内を下流へ伝播する様子, 背景流との相互作用, そして回折効果を示しています. 信号は 2.5 MHz の高調波搬送波で, ガウス分布のパルスエンベロープを持ちます. メインダクトの入口と出口には吸収層が配置されています. アニメーションは, 系の対称面における圧力信号の振幅のみを示しています. 前述の通り, この音響モデルは760万自由度を解析するものであり, 9.5 GB の RAM を搭載したデスクトップ PC で実行可能です.
超音波流量計の信号管を通る音響パルスの下流への伝播.
下の図は, 上流 (緑) と下流 (青) を伝播するパルスの受信信号を示しています. 2つの信号の到着時間差は49ナノ秒と測定され, これを用いて平均流速を推定すると 10.75 m/s という値が得られました. 実際の値は 10 m/s ですが, この差は, このモデルの重要なパラメーターであるフロープロファイル補正係数 (FPCF) によるものであることが分かっています. シミュレーションによって流れ場は事前にわかっているため, シミュレーションを用いて FPCF の値を計算することができます. 流量計の形状を最適化し, 様々な検出信号をテストすることもできます.
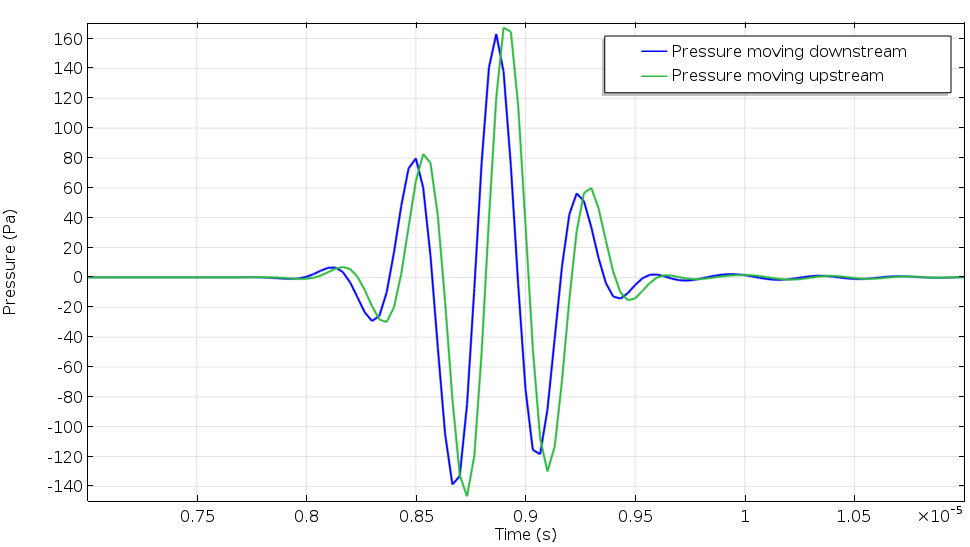
超音波流量計内を上流および下流に移動する信号の圧力信号プロファイル. 到達時間差は, 超音波流量計内の平均流速を予測するために使用されます.
対流波動方程式 (陽的時間発展) インターフェースにおける一般的なモデリングの考慮事項
編集者注: COMSOL Multiphysics® バージョン 5.3 以降では, DG 法を高速化するための新しいメッシュ品質最適化手順が利用可能になりました. この最適化はメソッドのパフォーマンスにとって重要であり, 可能な限り使用する必要があります. 詳細については, リリースハイライトページ または音響モジュールのユーザーガイドをご覧ください.
DG-FEM 定式化に基づく 対流波動方程式 (陽的時間発展) インターフェースを使用する場合, 知っておくとよい一般的なモデリング上の考慮事項がいくつかあります. 音響モジュールの FEM ベースインターフェースに関連する方法とは異なる方法もあります. これらのガイドラインは, 音響モジュールユーザーズガイド の対流波動方程式インターフェースを使用したモデリングセクションにも記載されています.
吸収層の設定
吸収層は, PML と同様に, モデルツリーの 定義 ノードから, 層を表すジオメトリエンティティに吸収層を追加することで設定します. (PML の場合, モデルのジオメトリを作成する際に レイヤー オプションを使用することをお勧めします. ) 吸収層を設定したら, 層の最外境界に音響インピーダンス境界条件を設定する必要があります. 上級ユーザーの場合, 通常はデフォルト値で十分機能しますが, 高度なフィジックスオプション を表示できるようにすることで, 最上位の物理レベルで吸収層のフィルターパラメーターを変更できます.
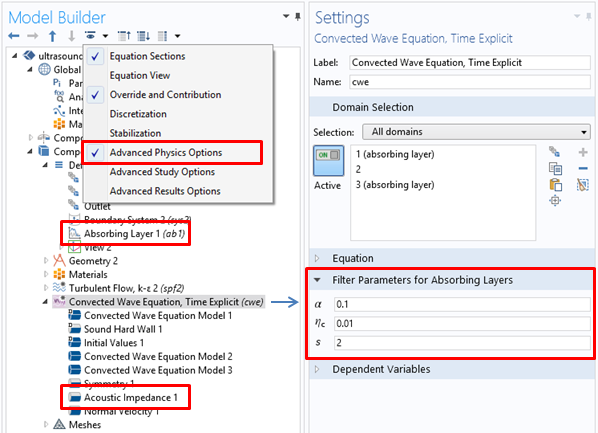
吸収層機能と音響インピーダンス境界条件の設定.
モデルのメッシュ生成
対流波動方程式 (陽的時間発展) インターフェースを用いたモデルのメッシュ作成は, 音響モジュールの他のほとんどのフィジックスインターフェースとは少し異なります. デフォルト設定は4次形状関数を使用するため, 通常, 要素サイズを λmin/2 から λmin/1.5 の範囲に設定したメッシュで適切な空間解像度を実現できます. 陽解法の内部的な時間ステップサイズは, CFL条件, つまりメッシュサイズによって厳密に制御されることに注意してください. つまり, モデル内の最小のメッシュ要素が時間ステップを制御するため, 可能な限り小さなメッシュ要素の使用は避けるのが賢明です. 対流波動方程式 (陽的時間発展) インターフェースで使用される内部時間ステップは, メッシュと物理特性に基づいて, COMSOL Multiphysics® ソフトウェアによって自動的に選択されます.
モデルサイズを削減するためのデータ保存
数百万自由度を含む大規模な過渡モデルを解析する場合, 出力データ量が非常に大きくなり, 保存ファイルが数 GB に及ぶ可能性があります. モデルサイズを削減するための優れた戦略は, ポストプロセスに必要なジオメトリエンティティ (例えば, 対称面, 直線, 点など) のデータのみを保存することです. COMSOL Multiphysics では, スタディステップ設定の 出力にフィールドを保存 機能 (従属変数の値 セクション内) を使用することで, これを簡単に実現できます. この機能では, 保存する選択データを指定できます. スタディ設定 セクションで指定される 出力時間 は, 解が保存される時間であり, 内部の時間ステップとは関係がないことに注意してください.
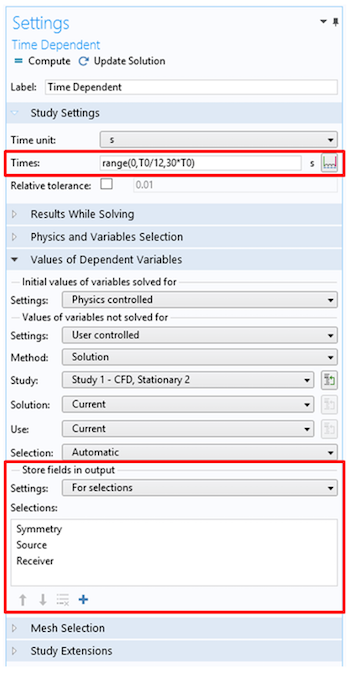
保存ファイルのサイズを縮小するには, 解を保存する時刻を設定し, 必要な選択範囲のみにデータを保存してください.
結果のポスト処理
対流波動方程式 (陽的時間発展) インターフェースを使用してシミュレーションを実行した結果を解析する際には, 4次要素が従属変数を離散化することを覚えておく必要があります. つまり, メッシュ要素内では, 形状関数の自由度が高く, 多くの空間詳細を含めることができます. これらの詳細を表示するには, プロットの 品質 セクションで 解像度 を高く設定します. モデルを解析すると, 生成されるデフォルトのプロットでは既にこのオプションが選択されており, カスタム解像度と 要素細分化 が 6 に設定されています. ユーザー定義のプロットを追加する場合は, 解像度を変更する必要があります.
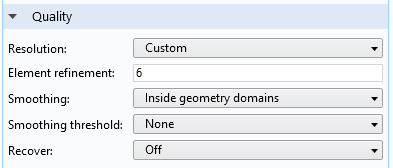
要素細分化 を 6 に設定してカスタム解像度を設定すると, 解の空間表現が良好になります.
デフォルトのプロットに設定されたカスタム解像度と, 追加されたユーザー定義プロットのデフォルトの解像度の違いの例を, 下の図に示します. 一見すると, 左側の解は間違っているように見えます. しかし, 品質 セクションで正しい解像度を選択すると, 解の真の波動特性が明らかになります.
解像度が正しくない場合の音速 (左) と, 高解像度で正しく設定されたプロット (右).
編集者注: ここで示されているパフォーマンス数値は, COMSOL® 5.3 のリリース により向上しています. 今後のソフトウェアバージョンでも, これらの数値の改善に取り組んでまいります.
COMSOL Multiphysics® における音響モデリングアプリケーションの詳細
- このブログで紹介されているモデルをダウンロードしてください:
- COMSOL ブログで, その他の 音響アプリケーション のモデリング方法をご覧ください.
- 音響モジュールのその他のアップデートについては, リリースハイライトページ をご覧ください.
参考文献
- A. D. Pierce, “Acoustics, An Introduction to its Physical Principles and Applications,” Acoustical Society of America (1991).
- A. D. Pierce, “Wave equation for sound in fluids with unsteady inhomogeneous flow,” The Journal of the Acoustical Society of America. 87, pp. 2292 (1990).






コメント (0)