COMSOL Multiphysics^®における非線形材料モデルのパラメーターの推定方法

機械系には, 非線形の材料挙動を示す部材が含まれることがよくあります. 例としては, シールやガスケットの大きな弾性変形, ゴムや生体軟組織の周期荷重時のひずみ速度依存性とヒステリシス, 金属の弾塑性流動とクリープなどが挙げられます.

非線形構造材料モジュールアドオンと合わせて, COMSOL Multiphysics^®ソフトウェアには, 非常に複雑な材料挙動のモデリングに使用できる100以上の材料モデルが組み込まれています.

しかし, このような—現象論的な—モデルの欠点は, 多くの材料パラメーターを含んでいることであり, 正確なモデリング予測を得るためには, 特定の材料ごとに最適化する必要があります.

本日のブログでは, 一般的な材料試験で得られた実験データから, 非線形最小二乗法を用いてこれらのパラメーターを推定する方法をご紹介します.

一般的な材料試験

材料パラメーターを推定するための出発点は, 関連する実験データを取得することです. 何が関連しているのかについては, 以前のブログで説明されているように, 材料の種類と最終用途で予想される荷重の種類に大きく依存します.

例えば, 等方性の線形弾性材料は, 1回の単軸試験で特性評価が可能です. ひずみ速度依存性や負荷履歴依存性を示す材料は, 異なるひずみ速度での緩和試験, クリープ試験, 繰返し試験などのさらなる実験が必要です. 部材が高温および/または変化する温度で動作する場合は, 材料特性の温度依存性も考慮する必要があります.

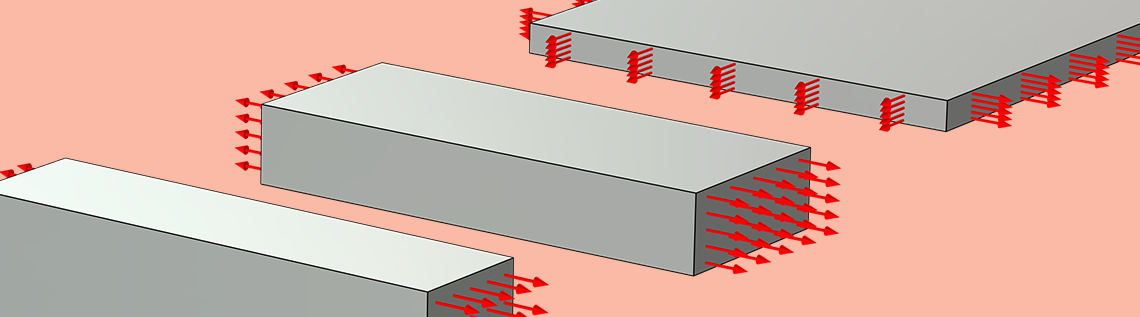
大きな変形を受ける材料の場合, 材料の挙動が等方的であっても, 異なる応力状態で試験することも重要です. 線形弾性と同じように, 1回の単軸試験で超弾性モデルを較正することは魅力的ですが, 圧縮荷重や2軸荷重の下でそのようなモデルを予測すると, 予期しない, あるいは不安定な材料挙動が得られる可能性があります. その代わりに, ゴム状材料の校正のために一般的に行われる実験の組み合わせには, 一軸引張試験, 純粋せん断試験, および等軸引張試験が含まれます. 薄いゴムシートのサンプルについて, このような実験を実現する方法の例を以下に示します.

左から右へ： 薄いゴムシートの一軸引張試験, 純粋せん断試験, 等軸インフレーション試験. 赤い矢印は, 所定の変位と, 膨張試験については加えられた膨張圧力を示します.

サンプルのアスペクト比を適切に選択した場合, 上に示した構成により, サンプルの中心部において均質な応力とひずみの状態が得られます. これらは, 加えられた変位や反力, あるいは加えられた圧力や膨張した膜の曲率半径などの測定可能な量から推定することができます. 応力とひずみの均質な状態をもたらす材料試験は, 単一の要素でモデル化できるため, 計算コストを大幅に削減できるため, パラメーター推定に特に適しています.

左から右へ： 等価な均質一軸引張, 純粋せん断, 等軸引張荷重ケース.

非線形最小二乗法によるパラメーター推定

実験データと材料モデルの選択が手元にあれば, 現在のモデル予測とデータを比較し, 差を最小限に抑えるために材料パラメーターを更新する最適化アルゴリズムを選択する必要があります. したがって, 未知の材料パラメーター \mathbf{q}^* を見つけることは, いわゆる逆問題を解くことに相当します.

これを重み付き最小二乗問題として数学的に定式化します.

ここで, \mathbf{W} は重みの行列で, \mathbf{r} はいわゆる欠陥 または 残差ベクトルと呼ばれます. これには, モデル予測 \mathbf{y} と実験データ \hat{\mathbf{y}}の差が含まれます.

モデル予測は, 材料パラメーターに陽的にまたは陰的に依存する場合があります. つまり, \mathbf{y} = \mathbf{y}(\mathbf{u}(\mathbf{q}), \mathbf{q}) です. ここで, \mathbf{u} は順問題の解です.

最小二乗問題のさまざまな構成要素をより適切に説明するために, 二次形式を次のように拡張できます.

ここで, N はデータセットの数です. Q_n と M_n は, それぞれ最小二乗誤差とデータセット n のデータポイントの数を示します. P_n(\mathbf{q}; \lambda_m) と \hat{P}_{n,m} は, それぞれモデルの予測と実験データです.

パラメーター \lambda_m は, 時間や適用されたストレッチなど, 実験の独立変数を示します. さらに, \mathbf{W} は成分 1/s_{n,m}^2 を持つ対角行列であると仮定しました. ここで, s_{n,m} は, さまざまなデータポイントとデータセットを重み付けし, 目的が無次元であることを保証するスケール係数です. 最小二乗問題は, パラメーターの下限と上限によって拡張することもできます. これを使用して, 材料モデルが不安定なパラメーター空間の非物理領域を除外できます.

COMSOL Multiphysics^® では, 最小二乗問題を解くためにいくつかの最適化アルゴリズムが利用できます. ほとんどの場合, 目的はパラメーターの適切に動作する関数であり, 問題は勾配ベースのLevenberg–Marquardtアルゴリズムを使用して効率的に求解できます.

簡単に言うと, Levenberg–Marquardt法は, 最小値から遠い場合の勾配降下方向の更新ステップと, 二次に近い収束が達成できる最小値に近づくGauss–Newtonのステップとを適応的に交互に行うことにより, パラメーターを反復的に更新します. 更新アルゴリズムで重要な量は次のヤコビアンです.

これは, 材料パラメーターの変化に対するモデル予測の感度を測定するものです.

ヤコビアンの評価は, 原則として, 最適化ソルバー内で解析的に実行できます. ただし, 問題が高度に非線形であり, 順モデルの評価が安価な場合は, ロバスト性と効率の観点から, ヤコビアンの有限差分近似の方が望ましい場合がよくあります.

ヤコビアンが正しく計算できない場合, 例えば目的が微分不可能な場合, 勾配を用いない2次近似による境界最適化（BOBYQA）アルゴリズムは, 微分の明示的な計算を必要としない代替アルゴリズムです.

オプションで, COMSOL Multiphysics^® の Levenberg–Marquardt ソルバーは, 推定パラメーターの不確実性の尺度として完全な共分散行列だけでなく信頼区間も計算できます.

これは, 実験データに分散があり, それを材料パラメーターに反映したい場合に特に便利です. 詳細については, 共分散分析によるパラメーター推定のチュートリアルを参照してください.

非線形材料パラメーターの推定例

以前のブログでは, 2つの一般的な荷重ケースに対して導き出された応力-ひずみ曲線の解析式を用いて, 超弾性モデルの材料パラメーターを推定する方法を探りました.

しかし, このアプローチは, 閉形式の解析解が存在しないことが多い非弾性材料モデルに簡単に拡張することはできません. その代わりに, COMSOL Multiphysics^®の組み込み材料モデルを活用することができます. 超弾性と大ひずみ粘塑性の2つのケースについて, このアプローチを示します.

超弾性 Ogdenモデルのパラメーター推定

最初の例では, 超弾性 Ogden モデルを, 軟質エラストマーを代表する一軸引張, 純粋せん断, および等軸引張のデータにあわせて適合させます. そのデータを以下に示します.

軟質エラストマーを表す一軸張力, 純粋せん断, 等二軸張力のデータ. 等二軸応力ははるかに大きいため, 2 番目の y 軸にプロットされることに注意してください.

エラストマーは非圧縮性であると仮定し, Ogden のモデルのひずみエネルギー密度は次のようになります.

ここでは, ひずみエネルギー密度関数の 2つの項が考慮され, 問題は, 下の画像に示すように, ４つの未知の材料パラメーター\mathbf{q} = (\mu_1, \alpha_1, \mu_2, \alpha_2)も解きます.

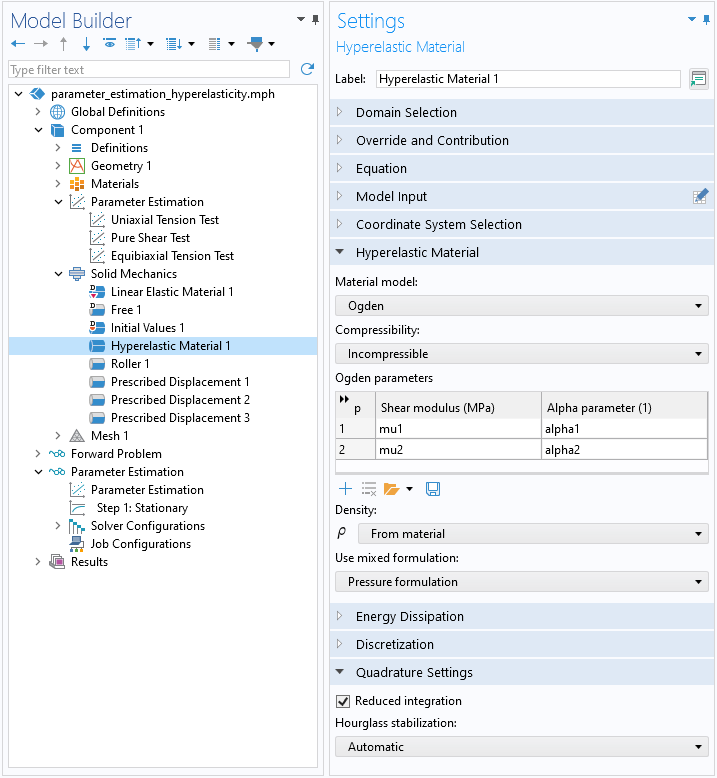
2つの項を含む非圧縮性 Ogden モデルの設定. 荷重ケースは均一であるため, 次数低減積分を使用して計算コストを削減できることに注意してください.

材料モデルを設定した後, データセットを結果テーブルにインポートし, グローバル最小二乗目的関数機能を使用して対応するモデル式にリンクできます. 下の画像は, 一軸データから形成された最小二乗目的関数の設定を示しています. モデル式フィールドで使用される変数 comp1.P_ua は, 公称応力の組み込み変数 solid.PxX の体積平均として定義されます.

一軸張力データに関連付けられたグローバル最小二乗目的関数機能の設定.

パラメーター推定スタディステップでは, 3つの目的関数を追加し, 推定する材料パラメーターを指定します. 推定パラメーターテーブルでは, mu1 と alpha1 は正の値に制限されていますが, mu2 と alpha2 は必ずマイナスになります. これらの境界により, 材料モデルが Ogden モデルの既知の安定性要件 \mu_p\alpha_p > 0 を満たすことが保証されます.

パラメーター推定スタディステップの設定.

解の進行状況は, 現在のモデル予測と実験データを比較するプロットで, 最適化ソルバーの反復ごとに監視できます. 以下のアニメーションに見られるように, Levenberg–Marquardt アルゴリズムは, 一軸および純粋なせん断モデルの予測を迅速に改善し, さらに数回反復すると, 高度に非線形な等二軸応答も同様に改善します.

粘塑性Bergstrom–Boyceモデルのパラメーター推定

次の例では, 粘塑性ポリマーのより複雑な Bergstrom–Boyce 材料モデルを検討します. このモデルは, ひずみ速度, 荷重履歴, および温度に依存する挙動を示します. 室温における2つの異なるひずみ速度での繰返し単軸引張および圧縮試験から得られた代表的な応力–ひずみ曲線を以下に示します.

粘塑性ポリマー材料の代表的なモデルの 2 つの異なるひずみ速度 (0.1%/s および 10%/s) での一軸引張および圧縮における荷重–除荷曲線.

Bergstrom–Boyce 材料モデルは, COMSOL Multiphysics^® バージョン 6.2 の超弾性材料機能のポリマー粘塑性サブノードで利用できます. ここで, 親超弾性モデルは弾性平衡ネットワークを定義し, サブノードは弾性要素と非弾性要素の両方を含む並列非平衡ネットワークを追加します. この例では, ほぼ非圧縮性の Arruda–Boyce ひずみエネルギー密度を使用して弾性要素をモデル化し, 粘塑性流れにおけるひずみ硬化と応力硬化の両方を含めます. 合計で, 材料モデルには6つの独立した材料パラメーター\mathbf{q} = (\mu_0^\textrm{eq}, N_\textrm{c}, \beta_\textrm{v}, A, c, n)が含まれています. ここで:

1. \mu_0^\textrm{eq}: 平衡ネットワークのせん断弾性率
2. N_\textrm{c}: チェーンセグメント数
3. \beta_\textrm{v}: 非平衡ネットワークと平衡ネットワークの間のエネルギー係数
4. A: 粘塑性流量係数
5. c: ひずみ硬化指数
6. n: 応力硬化指数

です.

ポリマー粘塑性機能の Bergstrom–Boyce モデルの設定. グラフィックスウィンドウには, 一軸圧縮および引張試験の単一要素モデルが表示されます.

最小二乗問題は, 超弾性の場合と同様の方法で設定し, 解くことができます. 下のアニメーションに見られるように, 最適化ソルバーが収束まで約12回の反復を必要とするにもかかわらず, 約5回の反復で視覚的に満足のいく解がすでに得られています. これは, Levenberg–Marquardtソルバーのデフォルトの終了基準が, パラメーターの増分または欠陥ベクトルとヤコビアンの間の最大角度が, 与えられた最適化許容値よりも小さいかどうかをチェックするためです. 最適化ソルバーの設定において, オプションで欠陥ベクトルの相対的な変化に基づく終了基準を追加することができます. これは, ソルバーがパラメーター空間において比較的平坦な局所最小値に達し, 目的関数の改善が小さい場合に有効です. 通常, デフォルトの終了基準は, 欠陥の減少に基づいて終了するよりもはるかに堅牢です.

材料モデルの安定性をテスト

非線形材料モデルのパラメーターを推定した後, 材料モデルをテストして数値的に安定していることを確認することをお勧めします. このトピックについては, このシリーズのパート 2 で詳しく説明します.

結論とさらなる研究

このブログでは, 典型的な材料試験のデータが与えられた場合に, COMSOL Multiphysics^®で非線形構造材料モデルのパラメーターを推定する方法を示しました. このアプローチは, どのようなタイプの材料モデルや材料試験データにも適用できます.

様々なモデルのパラメーター推定を自分で行うには, ステップバイステップのインストラクションの助けを借りて, アプリケーションギャラリの以下のモデルをチェックしてください：

• パラメーター推定:
  • 超弾性材料
  • 粘塑性ポリマー
  • 弾塑性材料
• 共分散分析によるパラメーター推定
• 複合粒子のマイクロメカニカルモデル