
以前のブログでは, ホログラフィックデータストレージ用の集束レーザービームのシミュレーションについて説明しました. より具体的な例では, フーリエレンズによって集束される電磁波は, レンズ入口での電磁界振幅をフーリエ変換することによって与えられます. フラウンホーファー回折の例を使用して, COMSOL Multiphysics でこの積分タイプの前処理と後処理を実行する方法を見てみましょう.
フラウンホーファー回折の例によるフーリエ変換の理解
シミュレーションでフーリエ変換を導入する機能は, さまざまなアプリケーションに役立つ機能です. フーリエ光学に加えて, フラウンホーファー回折理論におけるフーリエ変換, 周波数パターン抽出のための信号処理, およびノイズリダクションとフィルタリングのための画像処理で使用します.
この例では, 以下に示すように, メッシュカーテンを透過する信号機からの光の画像を計算します. モデルを単純化するために, 光の電場は均一な強度の平面波であると仮定します. たとえば, 1 V/mとします. メッシュジオメトリをローカル座標xとy光の伝播方向に垂直な平面で測定し, 画像パターンをローカル座標uとvメッシュ平面に平行な平面の目の近くで測定します.
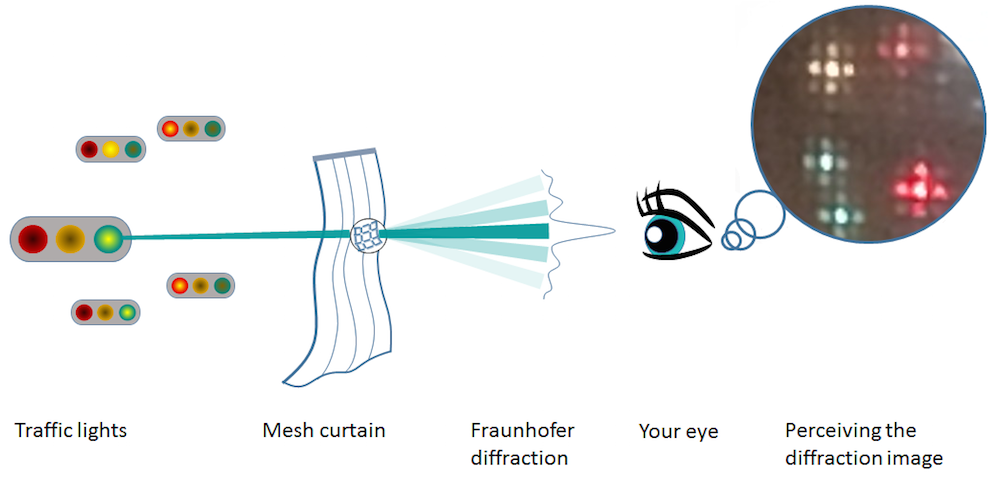
メッシュカーテンの正方形開口のフーリエ変換としてのフラウンホーファー回折パターン.
フラウンホーファー回折理論によれば, メッシュが正方形の場合は周期的な矩形関数である光透過関数をフーリエ変換するだけで, 上の画像を計算できます. 透過関数が単一の矩形関数である単一メッシュの単純化されたケースを考えてみましょう. 周期透過関数の場合については後で説明します.
ここでは, メッシュの1つの正方形に当たった光が, メッシュの中心部では透過しているのに, ファブリックの鋭いエッジで回折されることに注目しています. この場合, 光透過関数は2D矩形関数で記述されます. フーリエ変換をCOMSOL Multiphysics シミュレーションに導入することで, このプロセスをより深く理解することができます.
COMSOL Multiphysicsでのデータセットの活用
フーリエ変換を導入する方法を学ぶために, 最初にデータセット, または数値を格納する多次元行列の概念について説明しましょう. COMSOL Multiphysics には, 解とグリッドの2種類のデータセットがあります. どのような計算でも, COMSOL ソフトウェアはデータセットを作成し, それは結果> データセットノードの下に配置されます.
解データセットは非構造グリッドで構成され, 解データを格納するために使用されます. このデータセットを利用するために, 各列と行が対応するデータを指定します. 解1 (sol1)を指定すると, 行列の次元はスタディ1のモデルの次元に対応します. たとえば, 時間依存の問題の場合, データセットには3次元配列があり, これはT(i,j,k)とi=1,\cdots, N_t, \ j=1, \cdots, N_n, \ k = 1, \cdots, N_s で記述できます. ここでN_tは保存された時間ステップの数, N_nはノードの数, N_sは空間次元の数です. 同様に, 時間依存のパラメトリック スタディのデータセットは4D配列で構成されています. 繰り返しになりますが, 空間データ(時間およびパラメーターデータを除く)は, 必ずしも通常のグリッド上ではなく, メッシュ上の節点位置にリンクしていることに注意してください.
一方, グリッドデータセットには通常のグリッドが装備されており, 関数やその他すべての汎用用途に提供されます. グリッドデータセットに保存されているすべての数値は, 設定ウィンドウで定義されているグリッドにリンクしています. このデータセットは, 定義ノードで関数が定義され, プロットの作成をクリックすると自動的に作成されます. これにより, データセットノードに1Dグリッドデータセットが作成されます.
また, 独立変数の範囲と解像度を指定する必要があります. デフォルトでは, 1Dグリッドデータセットの解像度は1000に設定されています. 独立変数(つまり, x)の範囲が0〜1の場合, グリッドデータセットは0, 0.001, 0.002, …, 0.999, および1のデータ系列を準備します. デフォルトの解像度は2Dの場合は100, 3Dの場合は30です. フーリエ変換には, グリッドデータセットを使用します. このデータセットは解を参照していないため, 計算用の独立したツールとして使用することもできます.
フーリエ変換の導入
シミュレーションを開始するには, 次の画像に示すように, 組み込みの1D矩形関数を定義しましょう.
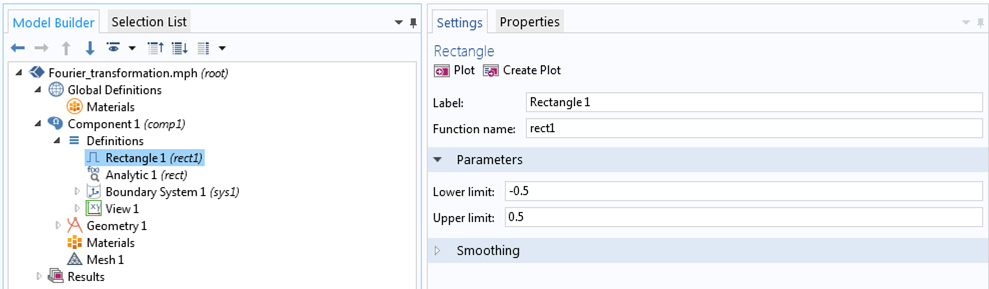
組み込みの1D矩形関数を定義します.
次に, 設定ウィンドウのプロットの作成ボタンをクリックして, 結果ノードに別の1Dプロットグループを作成します.
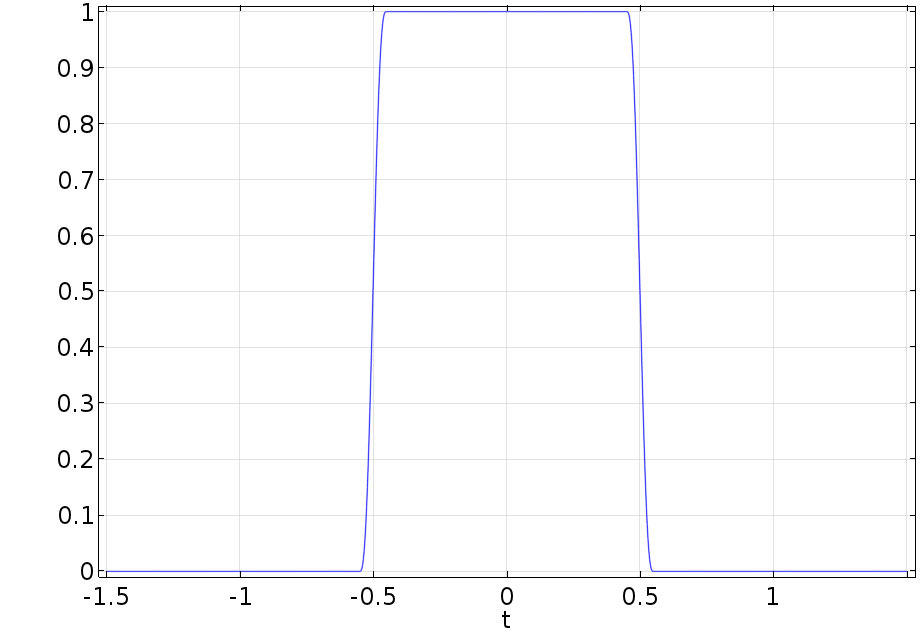
組み込みの1D矩形関数のプロット.
プロットの設定ウィンドウを見てみましょう. 1Dプロットグループ1ノードを展開し, ライングラフ1をクリックして, グリッド1Dを指すデータセットを表示します. グリッド1Dノード設定では, データセットが関数rect1に関連付けられていることがわかります.
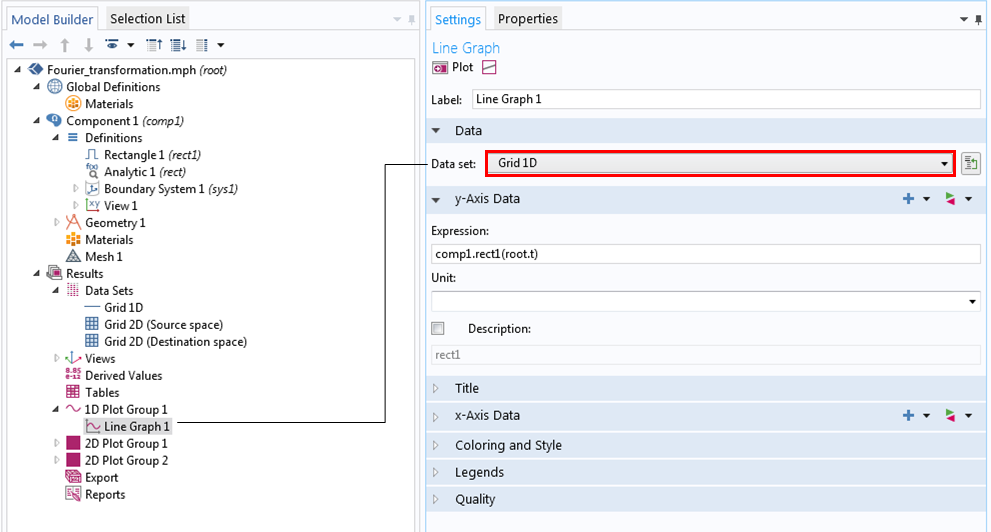
組み込みの1D矩形関数の設定.
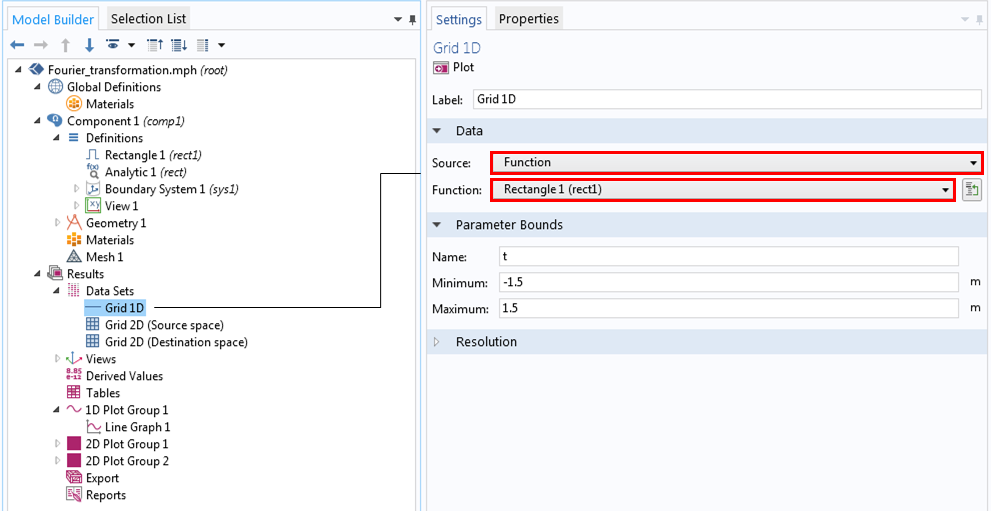
1D グリッドデータセットの設定.
定義ノードで解析関数をrect1(x)*rect1(y)として定義することにより, 2D矩形関数を作成できます. 学習目的で, 2Dグリッドデータセットを作成および定義し, 自動ではなく手動でプロットします. 結果を次の一連の画像に示します.
グリッド2D設定では, 2D矩形関数が別の関数rect1を使用するため, 関数にすべてを選択します. また, 先に定義したカーテンのローカル座標として定義した独立変数としてxとyを割り当て, より迅速なテストのために解像度を64に設定します. 結果をプロットするには, グループのプロット設定ウィンドウのデータセットに対して, グリッド2D(ソーススペース)に名前が変更された2Dグリッドデータを選択します.
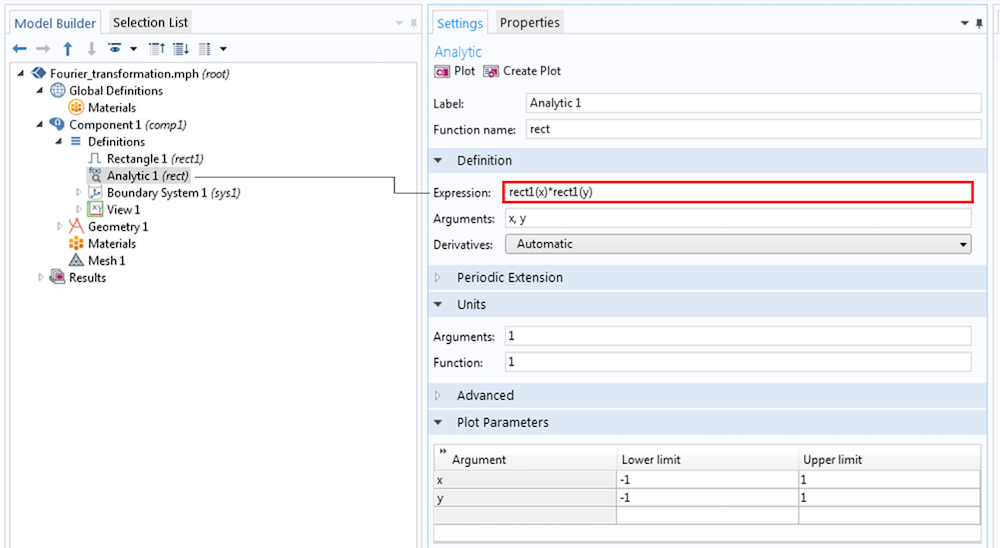
グリッド2D設定で関数を定義します.
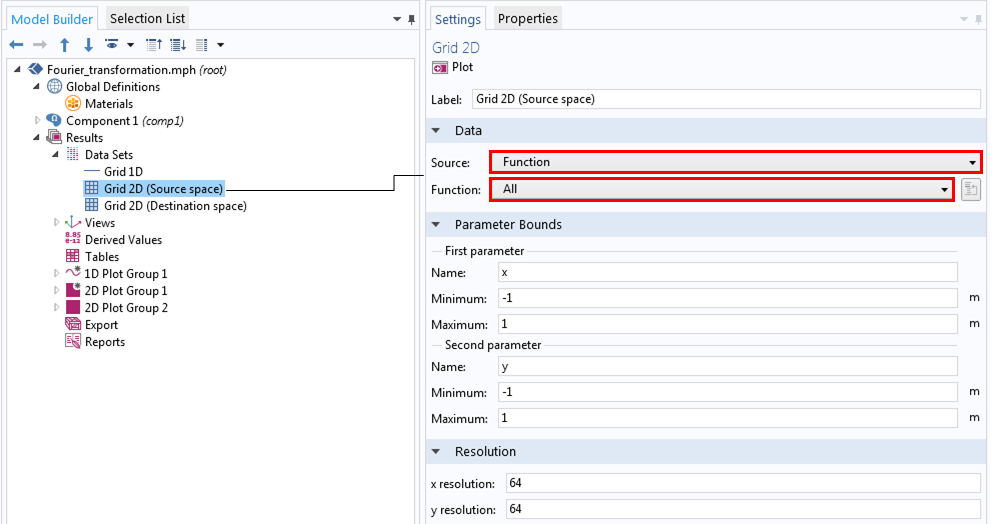
2Dデータセットの作成と定義.
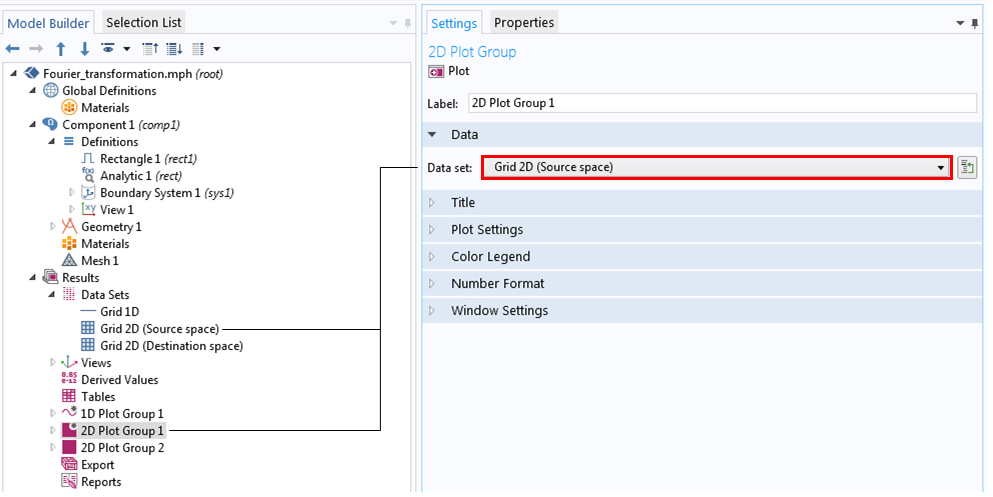
2D矩形関数の2Dプロットグループを設定します.
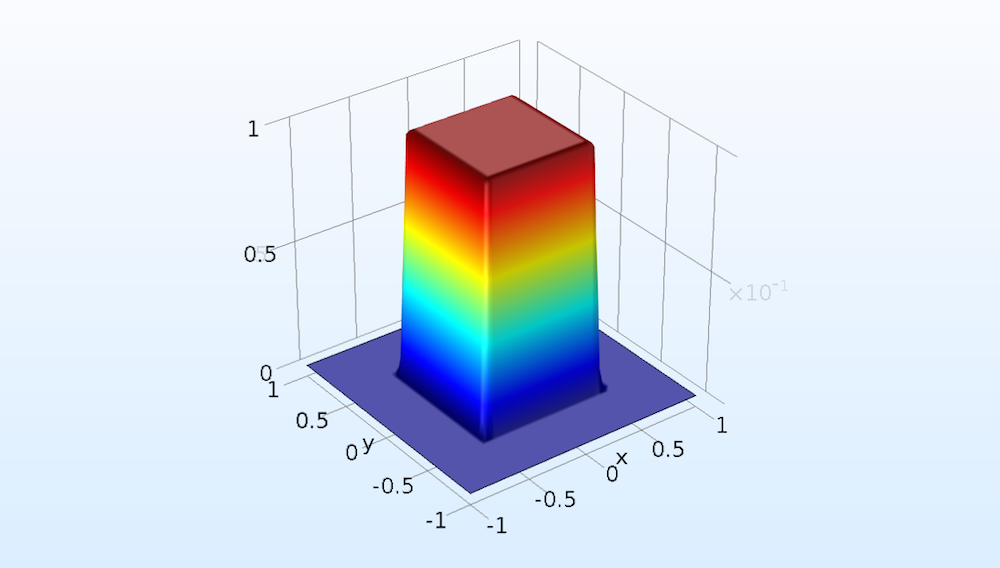
2D矩形関数の2Dプロット.
それでは, 以下を計算して, この関数のフーリエ変換を導入しましょう.
ここで, uとvは, 前に説明したように, 行先空間(フーリエ/周波数空間)の独立変数を表します.
xとyの2Dデータセットをすでに作成しているので, uとvのグリッド2D(宛先スペース)に名前が変更されたグリッド2Dデータセットを作成できます(以下を参照). rect関数は rect1関数も呼び出すため, ソースから関数と関数からすべてを選択します. 2Dデータセットの場合と同様に, ここで解像度を64に変更して, 計算を高速化できます.
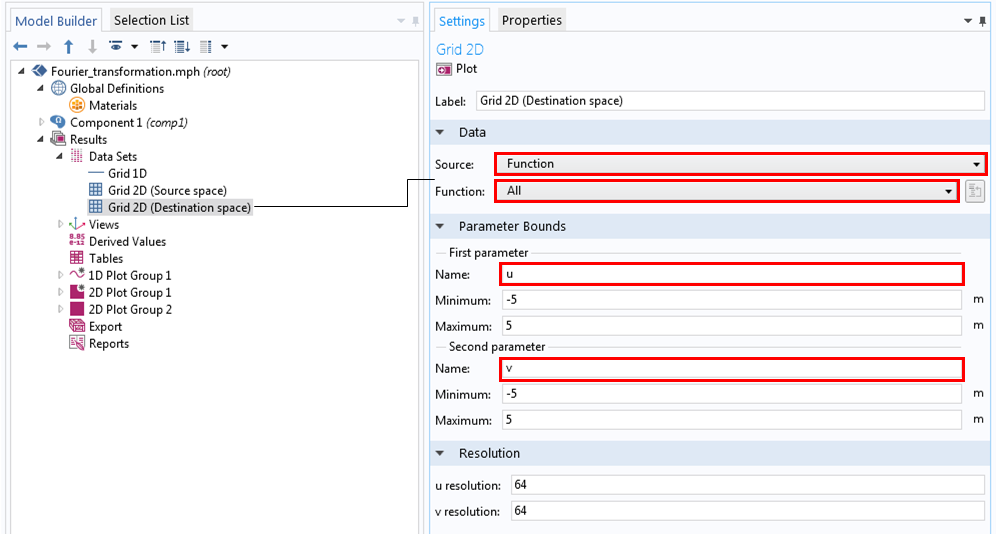
フーリエ空間のグリッド2Dデータセットの設定.
これで, 積分演算子を使用して方程式を入力できるシミュレーションの段階になりました.
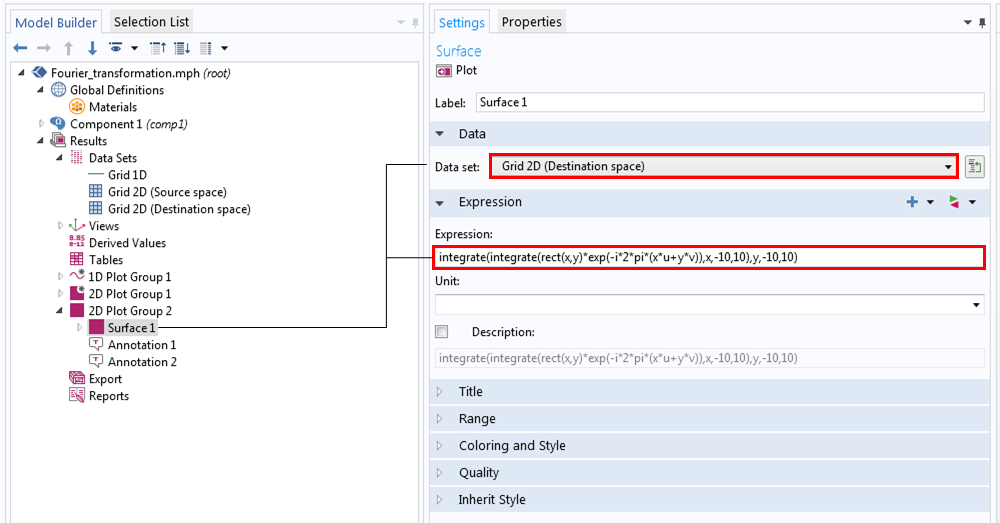
2D矩形関数のフーリエ変換の方程式を入力.
次の図に示すように, 最終的に結果のフーリエ変換を取得します. これ(より正確には, これの2乗)をメッシュカーテンの写真のそれぞれのきらめく色の光と比較します. 実際には, この画像はまだ実際には見られていません. 最終目的である目の網膜の画像を計算するには, フーリエ変換をもう一度導入する必要があります.
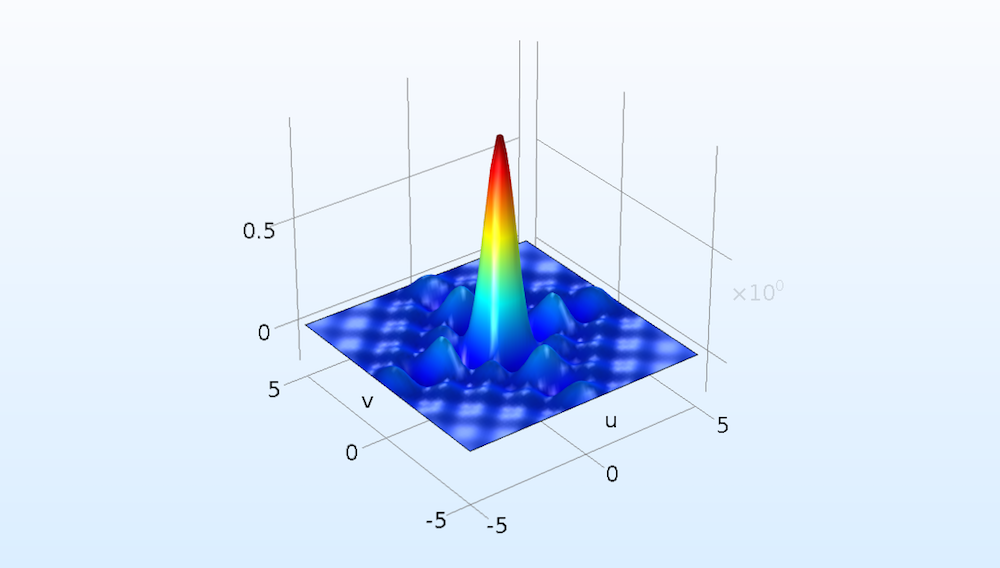
2D矩形関数のフーリエ変換.
フーリエ変換に関する結論
COMSOL Multiphysics,では, データセット機能とintegrate演算子を, 便利なスタンドアロン計算ツールとして, またメイン計算の前後の前処理および後処理ツールとして使用できます. ここで説明したフーリエ変換は, 離散フーリエ変換(FFT)ではないことに注意してください. シンプソンルールを使用した離散数学を使用してはいますが, 数値積分を実行します. これに対して離散フーリエ変換は数値シーケンスの演算によって形成されます. この関数は COMSOL Multiphysics の積分演算子で使用されます. その結果, エイリアシングの問題, フーリエ空間の解像度の問題, またはフーリエ空間のシフトの問題を気にする必要はありません.
このテーマについてはまだ議論する必要がありますが, 前に簡略化した2つのケースについてコメントしましょう. 単一メッシュについて計算しました. 実際には, メッシュカーテンは有限数の周期的な正方形の開口部でできています. 周期的な場合の計算をやり直さなければならないように思えますが, 幸いなことに, 最終結果は周期性の包絡線関数の分だけしか変わりません. 詳細については, Hecht の光学がこのトピックの概要を説明しています.
2番目の簡略化は, メッシュ伝達関数にシャープな矩形関数を想定したことです. COMSOL Multiphysics では, 数値の安定性と精度の理由から, ユーザー定義関数以外のすべての関数がある程度平滑化されます. お気づきかもしれませんが, ここで使った矩形関数の平滑化スロープは小さいものでした. このことが問題を少し複雑化するかもしれません. 数学的に最も単純なのは平滑化されていない矩形関数なのに, スロープを持つ矩形関数を使用したからです.
2つの極端なケースのフーリエ変換が知られています. つまり, 傾きのない矩形関数はsinc関数(sin(x)/x)に変換され, ガウシアン関数は別のガウシアン関数に変換されます. sinc関数は, 回折効果を表す中心の周りに波紋がありますが, ガウシアン関数は波紋なしで減衰します. 平滑化された矩形関数は, これら2つの極値の間のどこかにあるため, そのフーリエ変換もsinc関数とガウシアン関数の間のどこかにあります. 前に述べたように, カーテンファブリックは鋭いエッジを持つことができないため, とにかく今回の結果はより現実に近い結果となる可能性があります.
参考文献
- ホログラフィックデータストレージシステムのシミュレーションについてのブログ:
- 光学に関する入門書:
- J.W. Goodman, Introduction to Fourier Optics, W. H. Freeman, 2004.
- E. Hecht, Optics, Pearson Education Limited, 2014.






コメント (0)