フィードバック制御系の理論では, 完全状態フィードバックの概念を用いて, 系のすべての閉ループ極を配置することが可能になります. 極は系の動的挙動に対応しているため, 任意の場所に配置することは非常に重要です. 状態空間コントローラーアドインを使用すると, COMSOL Multiphysics® ソフトウェアの系モデルに完全状態空間フィードバックコントローラーを追加することができます. このブログでは, 完全状態空間フィードバックについて簡単に復習し, アドインの使用方法を説明し, 例題を使ってデモンストレーションを行います.
完全状態空間フィードバックについて
完全状態空間フィードバックは, 系の閉ループダイナミクスが次のような形式であることを前提としています.
\boldsymbol{D} = 0の場合, 制御可能な系である限り, 特性方程式を解くことで, 系の極を任意に配置することができます.
アドインによる状態空間フィードバックコントローラーの実装
アドイン使用すると, モデルにいくつかの機能を実装することができます. COMSOL Multiphysics® バージョン 5.6 で利用可能な状態空間アドインでは, 閉ループ系の極を配置することができます.
コントローラーアドインの別の例として, 以下のブログをご覧ください. PIDコントローラーアドインを使った制御系のシミュレーション方法.
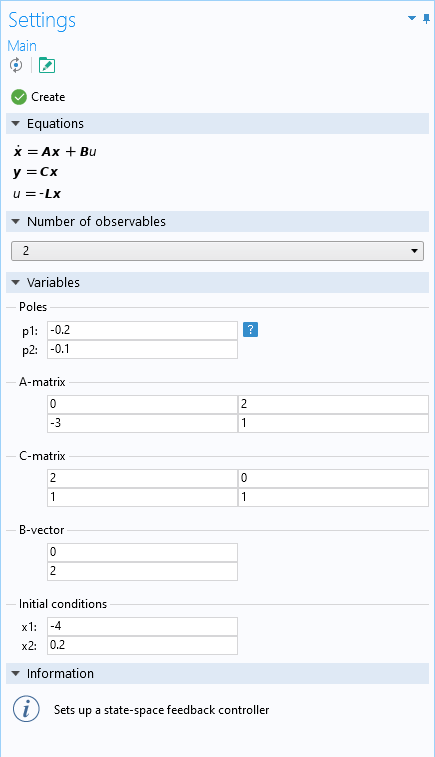
状態空間コントローラーアドインの設定画面.
目的の系に対する観測値の数, 行列\boldsymbol{A}と\boldsymbol{C}, ベクトル\boldsymbol{B}, 初期条件, 複素平面上の極の位置などを定義します. 続いてアドインは,グローバル方程式を用いてフィードバックコントローラーを定義する,新しい0Dモデルコンポーネントを作成します. 情報セクションでは, 関連するコンポーネントと, コントローラーの作成後に出力変数にアクセスする方法について説明しています. 制御変数はuとなります.
以下に, アドインの使用例を示します.
質量, ダンパー, バネの二重構造に対する力の例
例として, 質量m_{1}の点状の質量が, 一方ではバネとダンパーで壁に取り付けられ, もう一方では質量m_{2}の第2の点状の質量が, 同じくバネとダンパーで取り付けられている系を考えます. この2つ目の質量には, 力Fが作用しており, これを制御することで平衡状態を得ることができます.
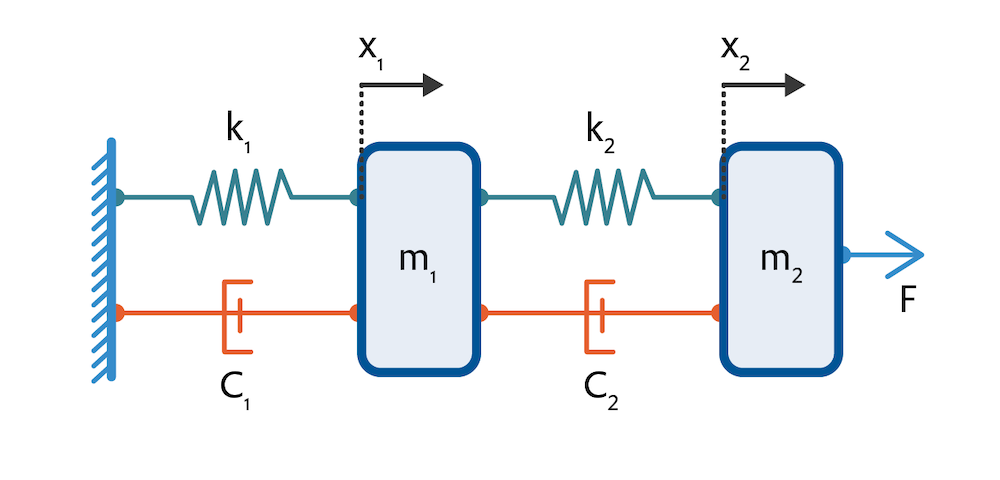
この系は, ニュートンの運動の第二法則のインスタンスであり, 時間微分を示すためにドット表記が使用されている以下の式で記述されます.
ここで, k_{1}とk_{2}は2つのバネのバネ定数, c_{1}とc_{2}は2つのダンパーの減衰定数, \tilde{x}_{1}と\tilde{x}_{2}は2つの質量のそれぞれの平衡位置からの偏差を表しています.
新たに4つの変数x_{1}=\tilde{x}_{1}, \, x_{2}=\dot{\tilde{x}}_{1}, \, x_{3}=\tilde{x}_{2},とx_{4}=\dot{\tilde{x}}_{2}を導入すると
の形式と
が得られます.
0 & 1 & 0 & 0\\
-(k_{1}+k_{2})/m_{1}& -(c_{1}+c_{2})/m_{1} & k_{2}/m_{1} & c_{2}/m_{1}\\
0 & 0 & 0 & 1\\
k_{2}/m_{2} & c_{2}/m_{2} & -k_{2}/m_{2} & -c_{2}/m_{2}
\end{pmatrix}, \, \text{ and } \boldsymbol{B} = \begin{pmatrix}
0 \\
0\\
0\\
1/m_{2}
\end{pmatrix}.
この場合, 制御変数であるuは力Fであり, \boldsymbol{C}はIDマトリクスを表しています. ここでは, パラメーターとして以下のように定数を定義します.
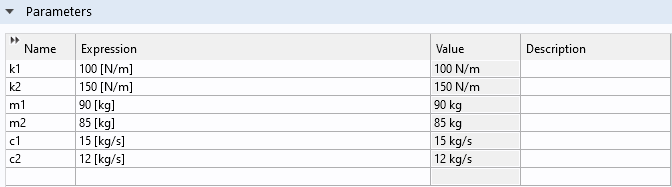
定数の定義.
ここで, 状態空間コントローラーを使用して, 閉ループ系の極を配置します. 4つの実数の極が必要で, すべて-0.5であると仮定します. 観測値が4つあるので, 以下のようにアドインを設定します.
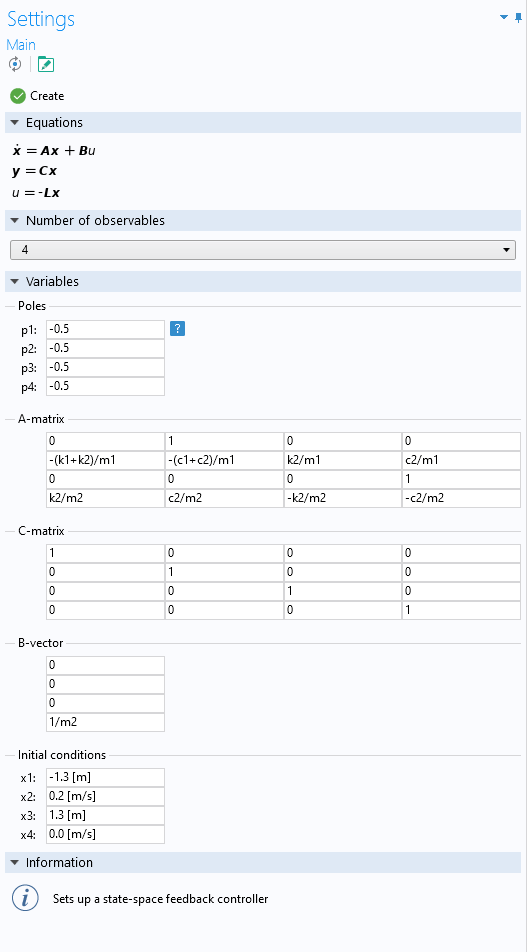
質量, ダンパー二重構造系の状態空間コントローラーの設定.
初期条件は, 1つ目の質量が平衡状態から負のx方向に1.3m, 速度0.2m/sでスタートし, 2つ目の質量が平衡状態から正のx方向に1.3m, 静止状態でスタートするように選択しました.
作成をクリックすると, 次のようなメッセージが表示されます.
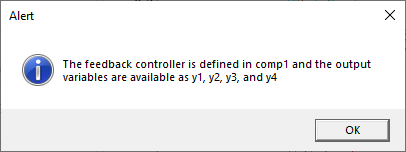
状態空間コントローラーからの出力変数の説明.
ここでスタディを実行し, 質量が平衡状態で3m離れていると仮定して, その位置の時間変化を見るために, 変数y1とy3+3をプロットしてみます. y1とy3は2つの質量の平衡位置からの距離なので, y3+3は2つの質量が3m離れているときの質量1の平衡位置からの質量2の距離になります.
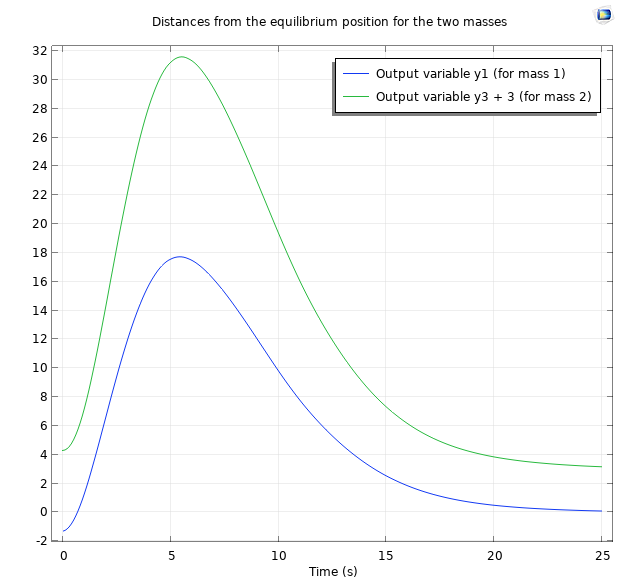
すべての極が-0.5に配置されている最初の25秒間の2つの質量の位置.
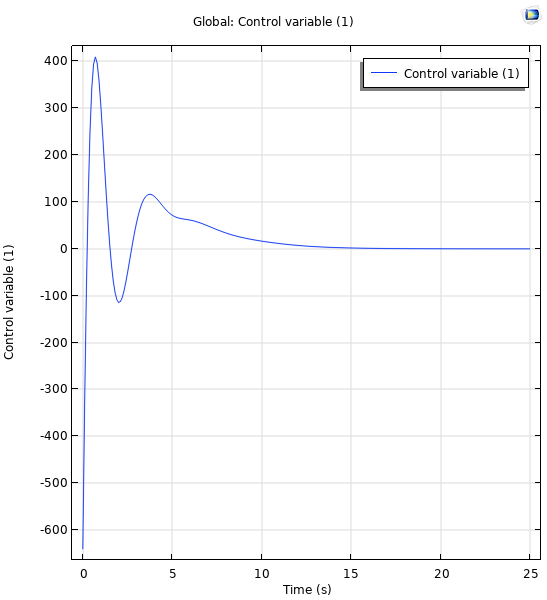
また, 制御変数uとしてアクセス可能な力をプロットすることもできます. 次のようなプロットが得られます.
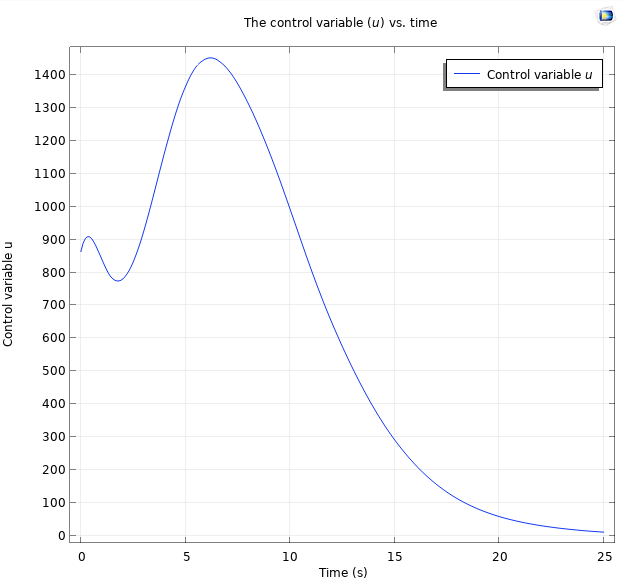
シミュレーションの最初の25秒間, すべての極を-0.5に配置したときにプロットされる制御変数.
例えば, 上記の系の安定化時間に満足していないとします. 制御理論的には, 負の実数面のさらに奥に極を配置すれば, 安定化時間が短縮されると考えられます. 上記の手順で, すべての極を-0.5ではなく-1に配置すると, 次のような位置関係のプロットが得られます.
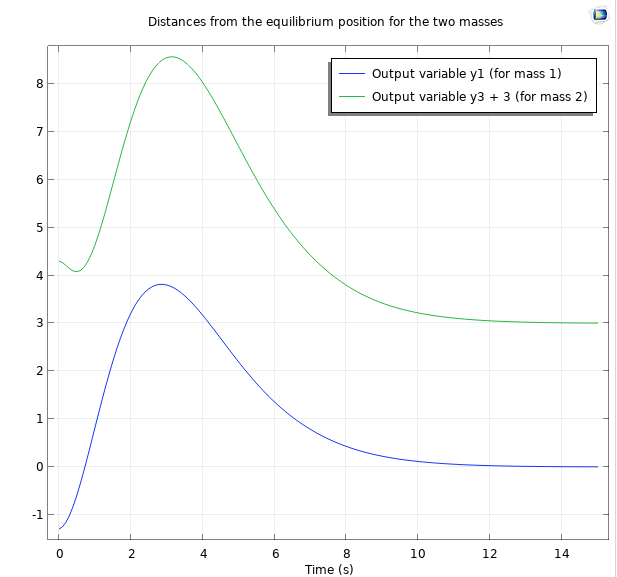
すべての極を-1にしたときの最初の15秒間の力のプロット.
さらに, 制御された力に対して以下のようなプロットが得られます.
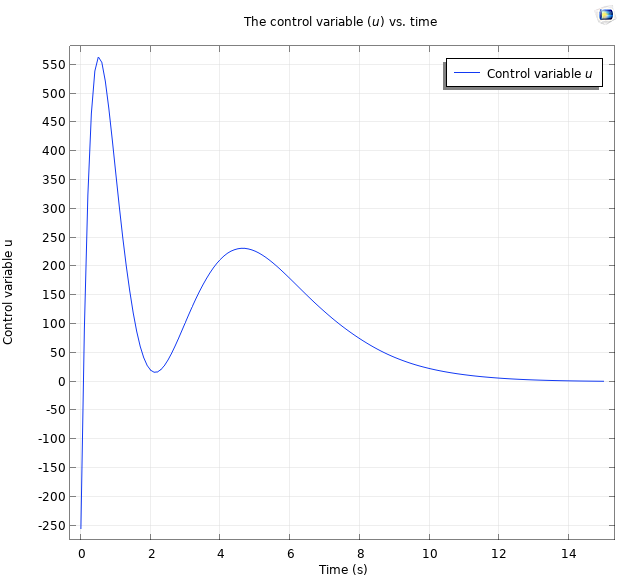
すべての極を-1にしたときの最初の15秒間の力のプロット.
予想通り, 系の安定化が早くなりました.
状態空間コントローラーアドインでは, 複素数平面に極を配置することもできます. 複素数の極は, 常に複素数の共役のペアになっています.
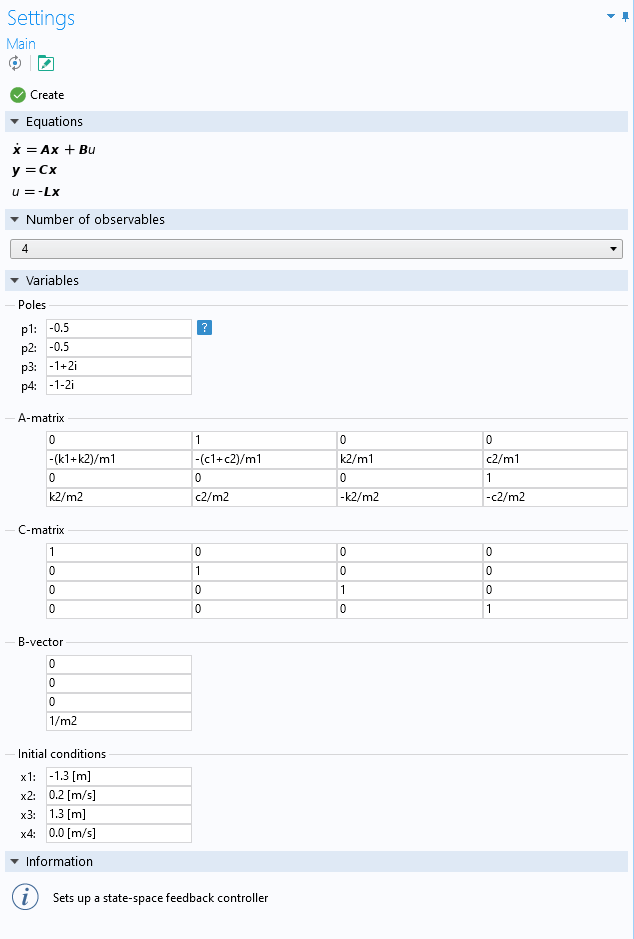
2つの複素極を持つ状態空間コントローラーの設定.
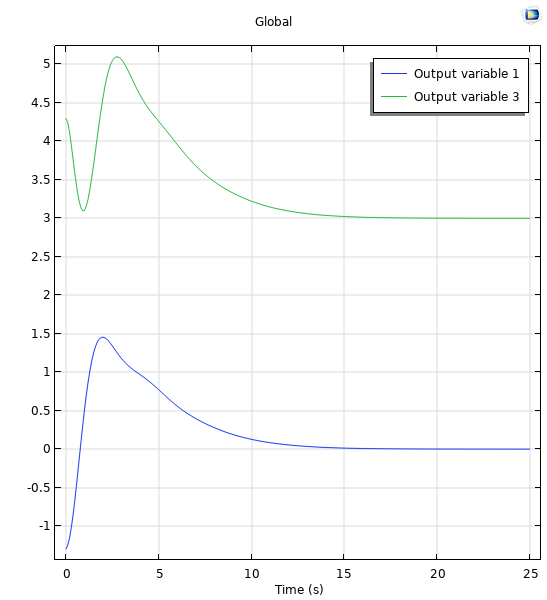
この結果, 位置と制御信号のプロットは次のようになります.
2つの実極を-0.5, 2つの複素極を-1+2iと-1-2iに配置した場合の位置プロット(左). 2つの実極が-0.5, 2つの複素極が-1+2iと-1-2iにある場合の制御信号のプロット(右).
極の配置
前節のシミュレーションで見たように, 閉ループ系の極をどこに配置するかによって, 系の挙動は大きく変化します. 極の配置が任意の系にどのような影響を与えるかについて, 一般的に説明することは困難です. しかし, 上記のような連続した系の極を配置することは, より早い安定化につながると同時に, 制御信号が大きくなる可能性があると言えます. 状態空間コントローラーアドインを使えば, 様々な極の配置に対する系の挙動を簡単に評価することができます.


コメント (0)