
会議室, コンサートホール, あるいは車などの室内にいるとき, 誰もが “音響” が良いか悪いかについて意見を持っています. 室内音響 では, この音質の概念を定量的に研究したいと考えています. 簡単に言うと, 室内音響は密閉空間の音響を評価することに関係しています. COMSOL Multiphysics の音響モジュールには, 部屋やその他の密閉空間の音響をシミュレートするツールがいくつかあります. ここでそれらを紹介します.
室内音響の概要
室内で音が発せられると, それを聴く人は音源からの直接音と壁からの反射音の組み合わせとして音を知覚します. 壁では, 音は反射, 吸収, 散乱します.
これらのプロセスはすべて周波数に依存するため, たとえば, 設計が不十分な会議室では, スピーチにとって重要な周波数帯域で反響が大きくなる可能性があります. また, 部屋は特定の重要な周波数で強いモード動作 (定在波) を示し, 簡単に励起される可能性があります. これらは, 部屋を設計するときに避けたいことであり, 予測できるようにする必要があります.
サウンド設計
建築家や土木技師は, 適切な場所に吸収体, 拡散体, 反射体を配置して音場を制御したいと考えています. コンサートホールでは, 聴衆がいる場所でのリスニング体験を最大化する必要があります. オフィススペースでは, 騒々しく感じられ, 従業員の集中を妨げる可能性のあるものはすべて避ける必要があります. 教室や講堂では, スピーチが明確に聞こえるようにする必要があります. 音環境はさまざまな理由で重要であり, 多くの場合, 音環境に関する国の基準や規制があるのはそのためです.
設計が不十分な部屋の改修には非常に費用がかかる可能性があるため, スケールモデルでの測定や事後に行われた測定だけに頼ることは避けてください. 設計を最適化し, 完璧にするためには, 事前に室内の音響挙動をモデル化しておくことが重要かつ不可欠です. シミュレーションモデルと測定では, 物理的な尺度 (メトリック) を使用して, 建築的側面 (形状) を主観的観察に関連付ける必要があります. これは, 残響時間, 初期減衰時間, 明瞭度, その他の多くの標準化されたパラメーターなど, 室内の音響のさまざまな尺度を計算することによって行われます.
採用するモデリングアプローチは, 調査対象の周波数 (部屋の幾何学的特徴と比較した波長) によって異なります. COMSOL ソフトウェア製品 の 音響モジュール では, 基本的に3つのフィジックスインターフェースにパッケージ化された3つのアプローチを提供しています. 圧力音響 インターフェースでは, 室内のモード挙動をモデル化できます. 音線音響 インターフェースと 音響拡散方程式 インターフェースでは, 高周波数限界または残響挙動 (幾何音響) をカバーします. 以下のセクションでは, インターフェースとその適用性について説明します.
小さなコンサートホール内で放出される音波の前面の位置のアニメーション. カラースケールは, 対数スケールでの音波の強度の印象を与えます.
物理的な室内音響
前述のように, 室内音響は, 通常, 研究対象の周波数に応じて3つのカテゴリに分類されます. または, より具体的には, 問題の部屋の特徴的な幾何学的構造物と比較した波長によって異なります.
低周波数範囲では, 部屋の共鳴が支配的です. これは, モード領域 として知られています. スケールの反対側の端, 高周波数限界では, 波長は部屋の特徴的な幾何学的構造物よりも小さくなります. ここでは, 残響領域または 幾何音響限界 を扱います. モードと高周波数限界の間には, いわゆる 遷移ゾーン があります. このゾーンの明確な定義がないことに注意してください.
古典的な室内音響理論は, 部屋の挙動を大まかに評価できるツールをいくつか提供しています. 特定の部屋では, Schroeder 周波数 f_\textrm{s} によって, 部屋のモード挙動と高周波残響挙動の間の限界周波数が予測されます.
Schroeder 周波数は次のように求められます:
(1)
ここで, V は部屋の容積, T_{60} は残響時間です.
この式は, 限界では3つの固有周波数が1つの共鳴半幅に収まるという基準 (Schroeder が提案) に基づいています. 残響時間 (または減衰時間) T_{60} は, 音圧レベル (インパルス音源によって生成される) が 60 dB 減衰するのに必要な時間です. 残響時間の最初の簡単な近似値は, よく知られている Sabine の式で与えられます:
(2)
ここで, c は音速, A は全吸収です. ここで, S_i と \alpha_i はそれぞれ ith 表面の表面積と吸収です.
これはおそらく室内音響で最もよく知られている式です. この式は, 純粋な拡散音場を仮定した古典的な統計的室内音響解析から派生したものです. 拡散音場では, 音圧レベルは均一で, 反射音が支配的です. この現象は, 残響音場 としても知られています. このような場では, 減衰定数 (全体的な吸収に関連) を近似することができ, 残響時間に関連します.
部屋や密閉空間のモード動作は, 有限要素法 を使用してヘルムホルツ方程式またはスカラー波動方程式を解くことで最もよく分析されます. Schroeder 周波数を超える周波数での残響または高周波限界では, 2つの異なるアプローチを使用できます. 選択は, 可能な仮定と必要な詳細レベルによって異なります.
音響拡散方程式 インターフェースは, すべての直接音を無視して, 純粋に拡散した音場限界で使用できます. これは, 結合された部屋の系で残響時間と音圧レベル分布を評価するための高速な方法です. 音線音響 インターフェースの音線追跡機能により, 直接音と初期反射を含む, より詳細な画像が提供されます. このインターフェースでは, インパルス応答を再構築することもできます.
圧力音響によるモーダル挙動
Schroeder 周波数までは, 定在波が残響特性を支配している部屋のモーダル挙動が重要です. 車内では, 遷移は数百ヘルツから 1000 Hz までの高さになることがあります. 小さなオフィスでは最大 200 Hz になることもありますが, 大きなコンサート ホールでは遷移は通常 50 Hz 未満です. 以下に示す小さなコンサートホールモデルでは, Schroeder 周波数は 115 Hz です (残響時間は約 1.3 秒, 容積は 430 m3). モーダル挙動は, たとえば映画館のサブウーファー系にとって重要です.
モード動作と室内の固有周波数は, 圧力音響 インターフェースを使用して分析するのが最適です. 周波数領域スタディでは, 低音系の伝達関数を再現できます. また, 死角を分析したり, 固有周波数を見つけたりするためにも使用できます. 過渡スタディは, たとえば, 車室内の低音の立ち上がりの過渡現象を調べるときに役立ちます.
ここで興味深いモデルは次のとおりです:

小さな部屋内の最初の固有モードの圧力分布. 室内固有モードモデル より.
音線音響による高周波挙動
音響音線の軌跡, 位相, 強度を計算する場合は, 音線音響 インターフェースを選択してください. 音線音響は, 音響波長が特徴的な幾何学的特徴よりも小さい高周波限界で作業する場合に適しています. このインターフェースは, 部屋やコンサートホールなどの閉空間での音響のモデリングに限定されず, 屋外環境でも使用できます. 外部境界では, 鏡面反射と拡散反射の組み合わせなど, さまざまな壁条件を割り当てることができます. 入射音線の周波数, 強度, 方向は, インピーダンスと吸収の両方に影響を与える可能性があります.
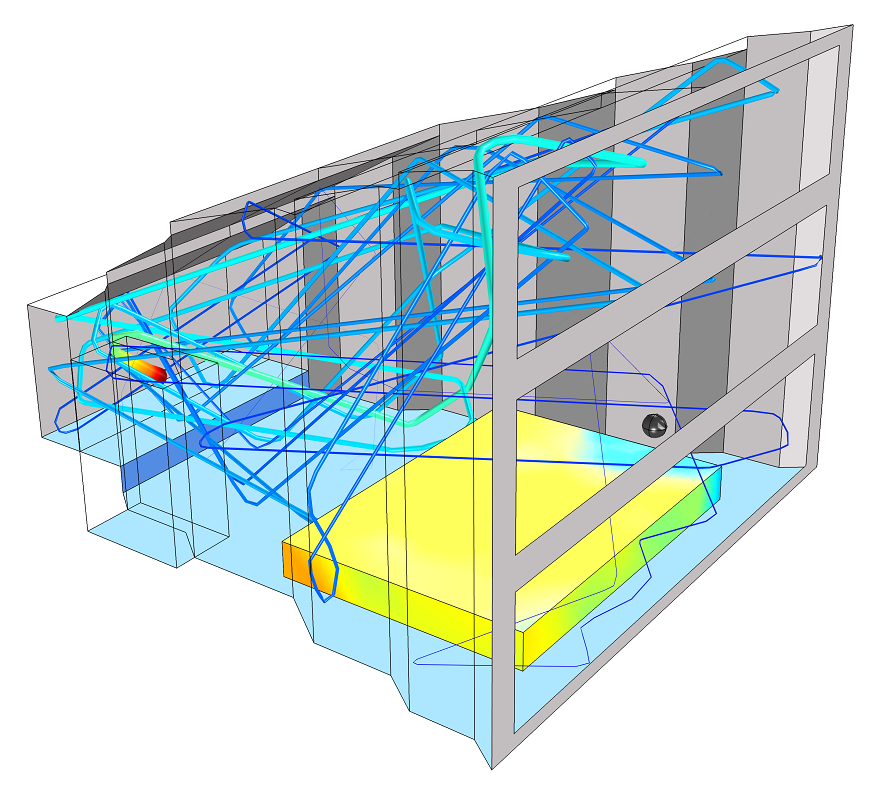
以下は, 音響モジュール のモデルギャラリにある 小型コンサートホールモデル からの2つの図です.
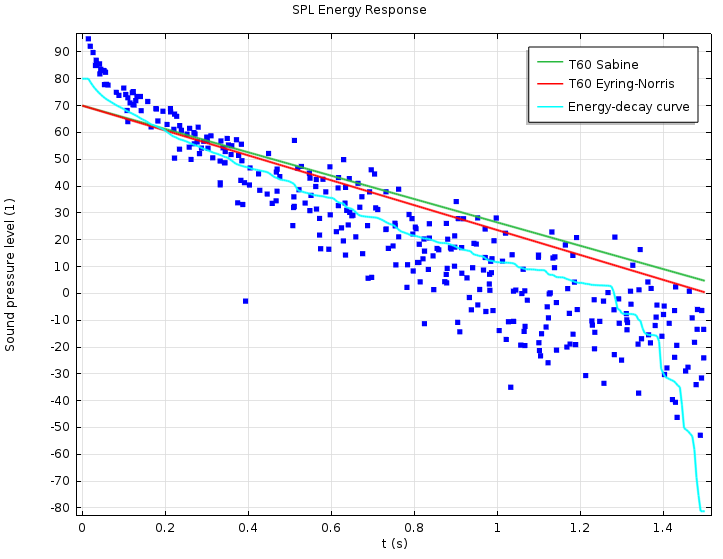
左の図は, 小さなステージにある音源から放射される, 選択された数の音線の音線経路を示しています. 右の図は, 部屋の中央で測定されたエネルギー応答を示しています. 点は, シミュレートされた音線応答 (5,000本の音線が放出される) を表し, 緑と赤の曲線は, 残響時間 T_{60} の単純な Sabine のような推定に基づく減衰曲線を表しています. シアンの曲線は, エネルギー応答のいわゆる Schroeder 積分 であり, エネルギー減衰曲線を生み出します. 応答を部屋の中央で測定すると, 4つすべてがよく一致します.
左: 小さなステージにある光源から放射された, 選択された数の音線の音線経路. 右: エネルギーインパルス応答を2つの単純な減衰測定とエネルギー減衰曲線と比較したもの.
音線音響 インターフェースを使用すると, コンサートホールの任意の点で応答を測定できます. 吸収体と拡散体の特性は, 周波数と入射角の両方に依存します. したがって, リスニング環境を適切に記述, 分析, および最適化できます. 単純な推定値は, 部屋のどこでも正確というわけではなく, 複雑な部屋の形状では正確ではありません.
音響拡散方程式による高周波挙動
音響拡散方程式 インターフェースは, 室内音響の音響エネルギー密度分布の拡散方程式を解きます. この方法は, エネルギー有限要素 と呼ばれることもあります. この方法は, 方程式 2 で Sabine 残響時間を計算するために使用される原理の拡張です. この特定のインターフェースは, 音響場が拡散している場合の高周波音響に適用できます. 音響エネルギー密度の拡散は, 平均自由音響経路, つまり部屋の形状に依存します. 壁で吸収を適用し, 部屋を結合するときに透過損失を適用できます. 部屋のフィッティングによる拡散の増加を追加できます. 材料特性と音源は, 周波数帯域で指定できます.
音線音響シミュレーションと比較すると, このインターフェースには位相情報, 直接音, または初期反射は含まれません. インターフェースは, 定常音響エネルギーまたは音圧レベル分布をモデル化するための定常スタディをサポートしています. 時間依存スタディを使用して, エネルギー減衰曲線と残響時間を決定できます. 固有値スタディを使用して, 結合された部屋と結合されていない部屋の残響時間を決定できます. 固有値は指数減衰時間に直接関連しているため, 残響時間にも直接関連しています.
私たちは, リビングルームに騒音源がある一戸建て住宅の音響を解析する 一戸建て住宅の音響モデル で, 3つのスタディタイプをすべて利用しました.
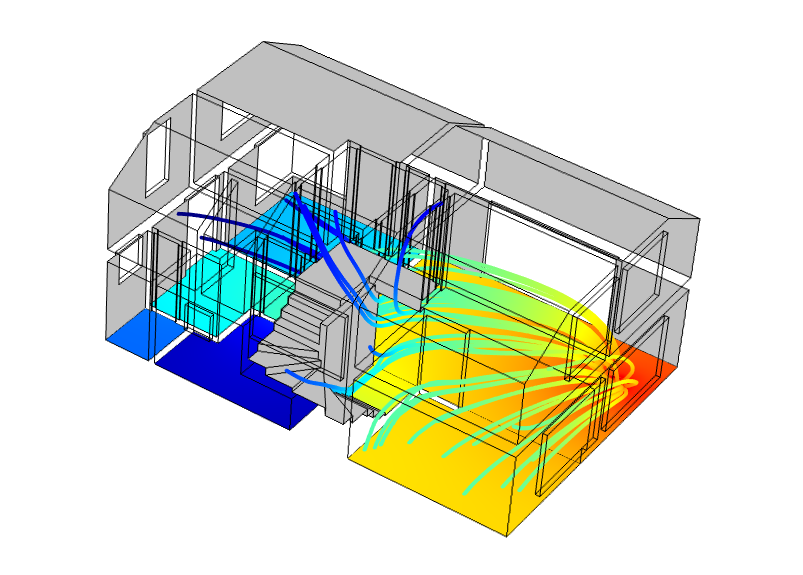
2階建ての一戸建て住宅内のエネルギー流束と SPL 分布.
その他の資料
この春, COMSOL ブログで, 音響拡散方程式 と 音線音響 フィジックスインターフェースに関するブログを確認してください.
それまでの間, 推奨される読み物のリストを以下に示します:
- H. Kuttruff, Room Acoustics, CRC Press, Fifth Edition, 2009.
- A. D. Pierce, Acoustics, An Introduction to its Physical Principles and Applications, Acoustical Society of America, 1991.
- ISO 3382 Standard, Measurement of room acoustic parameters.
- M. R. Schroeder, New Method of Measuring Reverberation Time, J. Acoust. Soc. Am., 37 (1965).
- M. R. Schroeder, Integrated-Impulse method measuring sound decay without using impulses, J. Acoust. Soc. Am., 66 (1979).






コメント (0)