前回のブログ, ゲージ固定とは? 理論的な紹介では, ゲージ固定の理論的背景, つまりゲージ固定がなぜ, どのような場合に必要なのかについて説明しました. ここでは引き続き, ゲージ固定の実装と, COMSOL Multiphysics® ソフトウェアでの使用方法について説明します.
ゲージ固定についての短いガイド: 通常は必要なし
前回のブログでは, AC/DCモジュールのフィジックスインターフェースの一部を形成するために使用される3つのポテンシャル, すなわち, 電気スカラーポテンシャルV, 磁気スカラーポテンシャルV_m, 磁気ベクトルポテンシャル\textbf{A}を紹介しました.
VとV_mの参照電位が定義され, \nabla \cdot \textbf{A}が指定されなければ, 電位は一意に決まらないことを示しました. 一意に決まらない場合, 解くべき数値問題は特異となります. この場合, COMSOL Multiphysics はデフォルトで, 解に収束する反復ソルバーを使用します. どのソルバーを使うかは重要ではありません. すべてのソルバーが同じ物理場(コンテキストに応じて\textbf{E}, \textbf{D}, \textbf{H}, \textbf{B}を生成します).
反復ソルバーと直接ソルバーの違いについては, こちらのナレッジベースのエントリーをご覧ください.
COMSOL Multiphysics のアドオンであるAC/DCモジュールでは, \textbf{A}場を解く3つのフィジックスインターフェースがあります.
- 磁場 (mf)は, \textbf{A}の定式化に基づいており, \textbf{A}が唯一の従属変数です. 静力学では, この解はゲージ固定なしでは一意に決まりませんが, 動力学では, 帰納的な項を追加することで, それらの項が数値的に有意であれば, 解は一意に決まります.
- 磁場と電場 (mef)は, 完全に結合した\textbf{A}とVを解きます. ゲージ変換のため, \nabla \cdot \textbf{A}を指定しない限り, 一意の解はありません.
- 回転機械, 磁気 (rmm), \textbf{A}定式化とV_m定式化の組み合わせ. 導電性(通電性) ドメインのモデリングには\textbf{A}定式, エアギャップやその他の非導電性ドメインにはV_m定式が用いられます. この2つの定式化は, 共通の界面境界で結合されます. rmmインターフェースは混合定式化なので, 磁場 (mf)インターフェースのゲージ固定に関するコメントが適用されます.
以下の表は, mf, mef, rmmの各インターフェースと, ゲージ固定なしのさまざまなスタディタイプの解の特性と必要な数値ソルバーをまとめたものです. これらの3 つのインターフェースにはデフォルトで反復ソルバーが搭載されているため, 通常, ゲージ固定は必要ありません.
|
インターフェース, 属性 |
固定 |
時間依存, \sigma=0 |
時間依存, \sigma>0 |
周波数領域, \omega>0 |
|---|---|---|---|---|
|
mf, rmm 解 |
非唯一 |
非唯一 |
唯一 |
唯一 |
|
mf, rmm ソルバー |
反復のみ |
反復のみ |
反復または直接 |
反復または直接 |
|
mef 解 |
非唯一 |
mfインターフェースの使用によって補われる |
mfインターフェースの使用によって補われる |
非唯一 |
|
mef ソルバー |
反復のみ |
mfインターフェースの使用によって補われる |
mfインターフェースの使用によって補われる |
反復のみ |
特筆すべきは, 電位に固有の解がない場合でも, 物理場である\textbf{E}と\textbf{B}は常に固有であるということです. 電位は直接測定できるものではなく, 物理的な意味を持たないので, 方程式を満たす解であれば何でもいいのです.
例として, アプリケーションライブラリで提供されているパワーインダクターのインダクタンスモデルを見てみましょう. このモデルはmefインターフェースで作成され, 最初はゲージ固定なし, 次にゲージ固定ありで, 周波数領域で解かれています.
下の図に示してあるように, Vの場は大きく異なりますが, \textbf{E}の場のノルムは予想通り不変です. 右上の図は, ゲージ固定を行った場合に, Vの場が領域内で滑らかに変化していることを示しています. これは, 左上の図のように, ゲージ固定をしない場合の場とは全く異なります. 興味深いことに, このゲージ(\nabla \cdot \textbf{A} = 0)はクーロンゲージと呼ばれます. これは, 静電電荷密度から生じるクーロンポテンシャルのように振る舞うVの場を強制するためです. 物理場である\textbf{E}と\textbf{B}が同じであるため, 計算上のリアクタンス値も一致します.
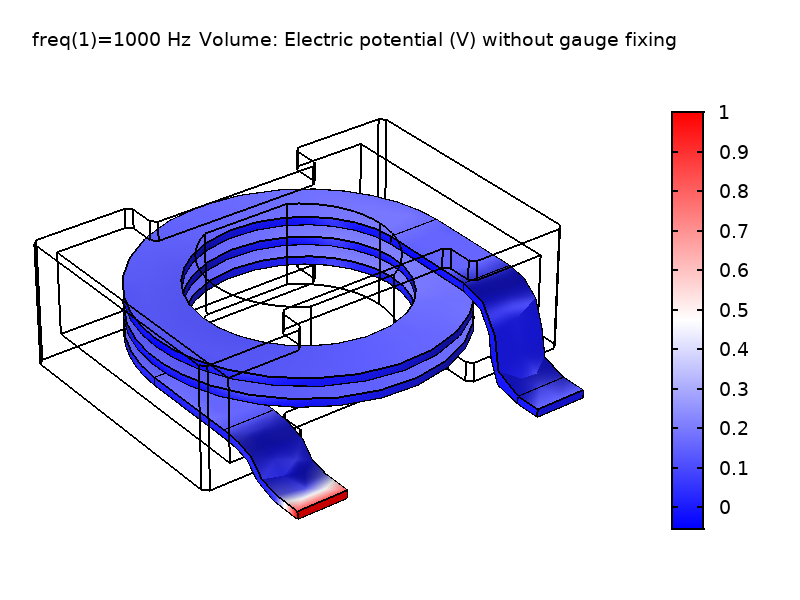
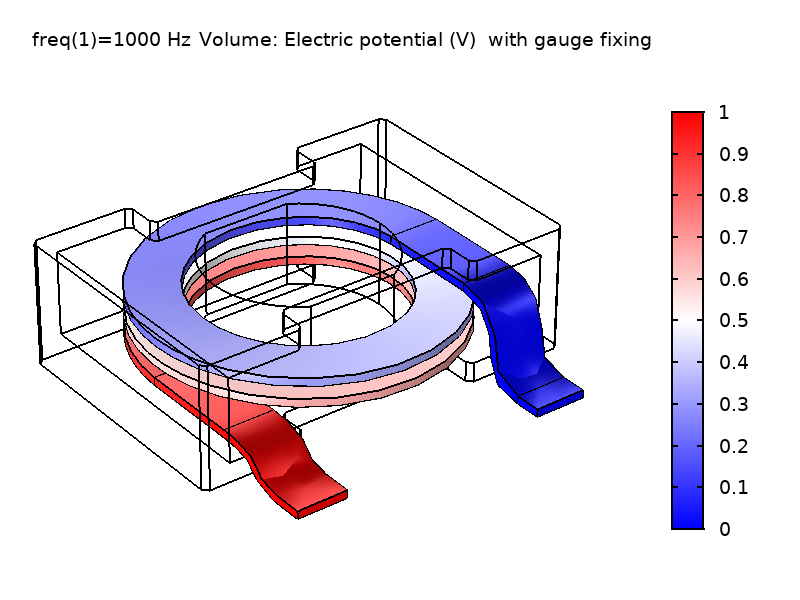
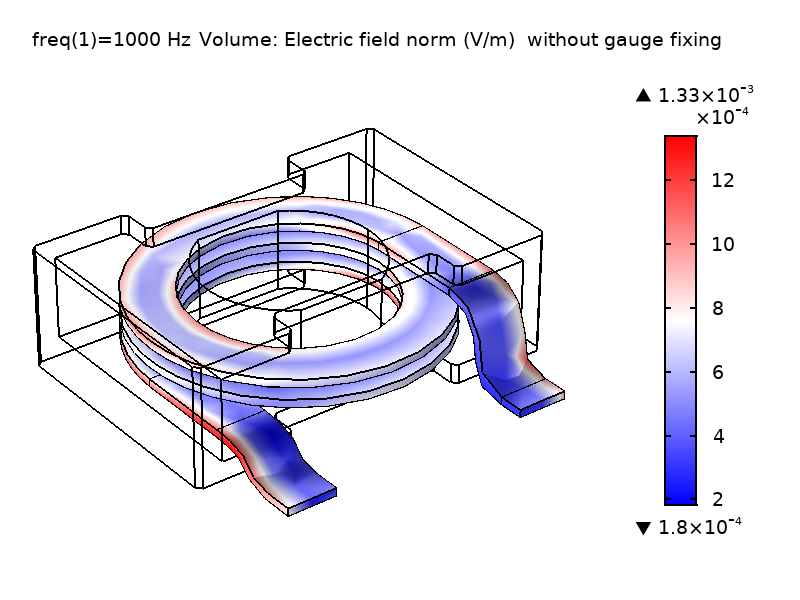
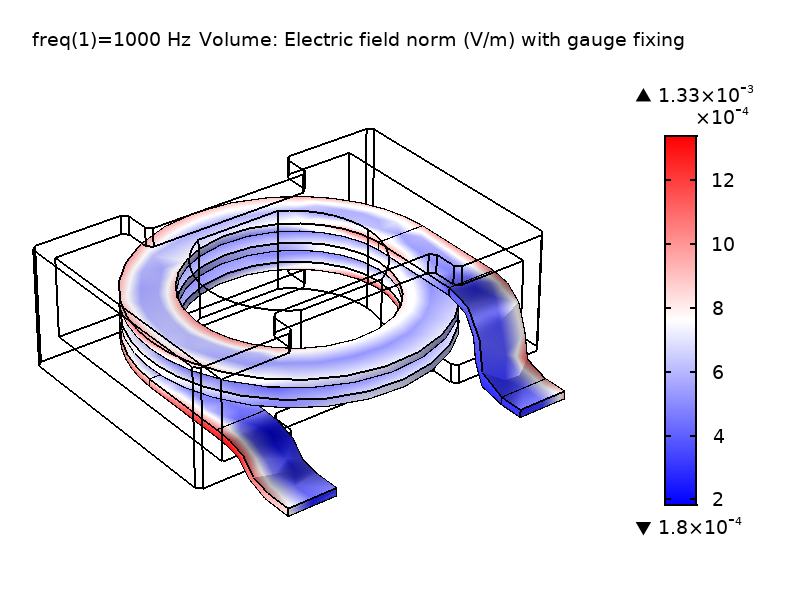
図1: ゲージ固定なし(左)とゲージ固定あり(右)で解いたコイル領域のV場と\textbf{E}場のノルムの比較.
AC/DCモジュールのゲージ固定方法
ゲージ固定は通常, \textbf{A}場の解が一意ではなく, 直接ソルバーを使用したい場合に必要となります. マルチフィジックスのカップリングを含むケースでは, 反復ソルバーと前処理は一般的に特定のタイプのフィジックスのみに合わせて調整されているため, 直接ソルバーの使用が必要または有益な場合があります. また, 2Dモデルを解く場合は, デフォルトで直接ソルバーが使用されます.
mf, mef, rmmの各インターフェースには, A場のゲージ固定というドメイン機能があります. この機能は, 面外ベクトルポテンシャルを2Dおよび2D軸対称でのみ解く場合を除いて利用できます. このとき, 面外方向のベクトルポテンシャルが一定であると仮定すると, クーロンゲージ\nabla \cdot \textbf{A} = 0が自明のこととして成立します.
A場のゲージ固定機能では, クーロンゲージを強制するためにラグランジュ乗数\psiを導入し, 結果として2つの連立方程式が発生します. 磁気学の例を見てみましょう. 1つ目の方程式(静的アンペアの法則)は\textbf{A}, 次のように表されます.
(1)
ここで, \textbf{J}_e は外部から印加された電流密度です.
2つ目の式は\psiに対するもので, クーロンゲージを表しています.
(2)
式1では, 変数\psiは, 非圧縮性ナビエ・ストークス方程式における圧力と同様の働きをし, 圧力は発散のない流れ場の制約を強いるものです.
式1が示すように, \psiの大きさには特別な意味はなく, その勾配のみが方程式に入ります(電位のように作用するということです). 式1の\nabla \psiの電流のようなものの項は, \psiが\textbf{A}に影響を与えるメカニズムを提供することで, 一連の式を締めくくっています. 非特異点モデルを生成するためには, 少なくとも1点で\psiの値を拘束することが重要です. デフォルトでは, この機能は磁気絶縁体の境界で\psiの値を, インターフェースで発散条件変数のスケーリング\psi_0(デフォルト値1A/m)を入力して設定できる値に拘束します. 下図は, 異なる\psiを使ったパワーインダクターモデルの\psi_0場と電場\textbf{E}の大きさを示しています. 見ての通り, \psiの大きさは\textbf{E}の大きさに影響しません.
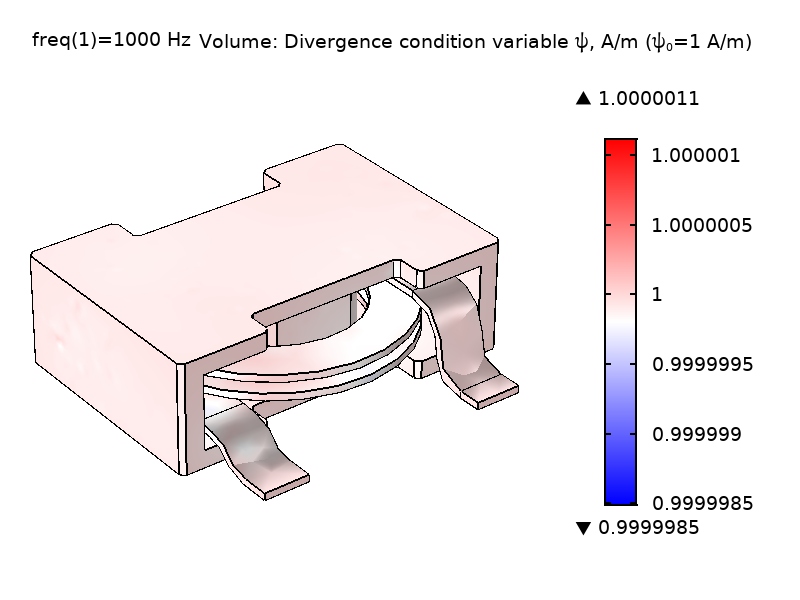
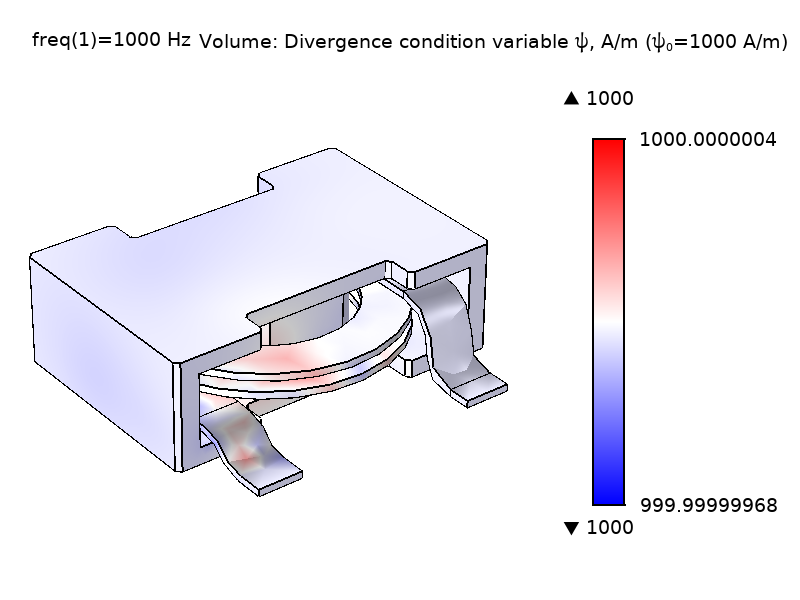
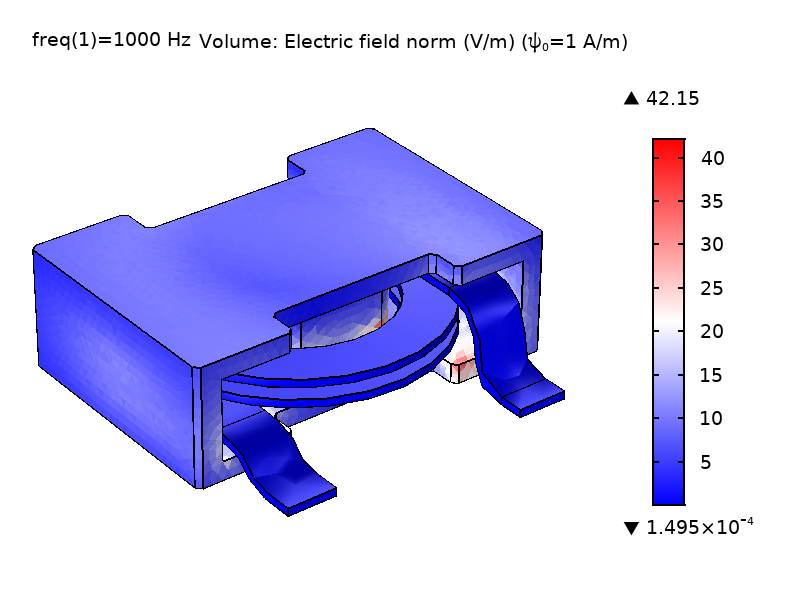
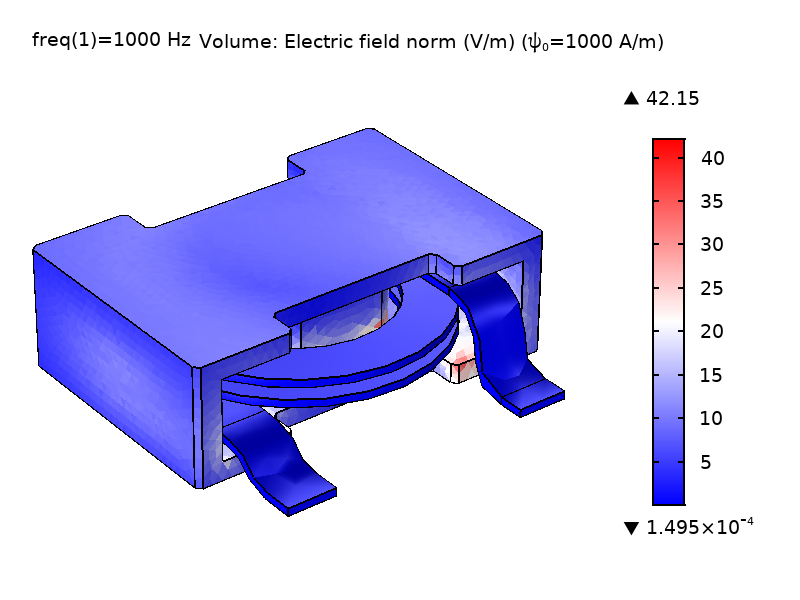
図2:異なる\psiスケーリングで解かれたコイルおよびコア領域における計算された\textbf{E}場および\psi場ノルムの比較. \psi_0 = 1 A/m (左), \psi_0 = 1000 A/m (右).
ゲージ固定を行うと, 未知数の総数が増え, 求解するのに必要なメモリと時間が増えるため, 必要な場合を除いて使用しないことをお勧めします. モデルによっては, ゲージ固定を使用すると, 計算時間が30~60%増加する可能性があります. また, ゲージ固定を行うと, システム行列の対角線上にゼロが存在することになってしまうという注意点もあります. 後者は, 直接ソルバーを使用する場合は問題ありませんが, 反復ソルバーでは, 前処理でより高価な手法を使用する必要があります(例: Vankaアルゴリズム). ソルバーの詳細については, COMSOL リファレンスマニュアルをご参照ください. デフォルトソルバーでは上記のような状況が通常考慮されているため, 一般的にはシステム行列の構造の変更を気にする必要はありません.
電流保存の強制: ゲージ固定のもう一つの役割
電流保存とは, アンペールの法則に固有のもので, 印加されたソース電流密度と誘導電流密度の和がソレノイドでなければならないことを意味します. このことは, マックスウェル方程式を解く際に重要になってきます. mfインターフェースの静的なケースでは, 解くべき方程式は次のように表されます.
(3)
式3の左辺と右辺の両方の発散を取ると, 次のようになります.
(4)
式4の左辺は, 任意の\textbf{F}に対して\nabla \cdot( \nabla \times \textbf{F}) = 0であるため, 定義によれば, ゼロであることにご注意ください. したがって, 右辺の外部ソース電流密度の発散もゼロでなければならず, そうでなければこの方程式は(まったく)解を持ちません. これにより, 式1で導入された変数\psiは, 実質的に2つの役割を果たすことになります. 式2を成立させるという当然の目的の他に, 式1に内在する\nabla \cdot (\textbf{J}_e + \nabla \psi) = 0という条件を成立させることになります. 言い換えれば, 式1に追加された項\nabla \psiは, 外部から印加された電流密度からの発散を排除し, 修正された右辺が必要な電流保存に適合するようにします. このため, ゲージ固定を, 解析的には無発散ではない外部からの電流密度と組み合わせて使用すると, 予想外の解が得られます. その場合, ゲージ固定によって\nabla \psi項に非物理的な大きな補償電流密度が導入され, モデルは予想外の結果を出すことになります. これは誤った解釈につながる可能性があり, このようなケースを検出するには, ゲージ固定で求解した後に\psi場を可視化することをお勧めします. \psi場は, 図2の上段に示すように, ゲージ固定が適用される領域では極めて小さな変動しかないはずです. そうでない場合は, 寄与されたソースの電流密度がアンペアの法則で要求されるソレノイド型でない可能性が高いです. ここで, 磁場 (mf)インターフェースの定常解に対するデフォルトの反復ソルバーは, 寄与されたソース電流に対して同様の補正を行うため, 物理場\textbf{B}に関しては, ゲージングされた解とゲージングされていない解が異なることはないということも付け加えておきます.
mfインターフェースの動的なケース(\sigma, \omega>0)では, 解は一意であり, \nabla \cdot \textbf{A} = 0を拘束する必要は通常ありません. mfインターフェースには, ゲージ固定を定常(\nabla \cdot \textbf{A} = 0)からスタディ制御に切り替えるオプションがありますので, その意味を詳しくご説明します. 時間依存のスタディでは, mfインターフェースは以下の方程式を解きます.
(5)
これは, 誘導された伝導電流密度は考慮しますが, 誘導された変位電流密度(いわゆる準静的近似)は無視するというものです. この場合, スタディ制御ゲージ固定は, \nabla \cdot \textbf{A} = 0を制約する代わりに, \nabla \cdot (\sigma \textbf{A}) = 0を強制することで電流保存を促すことになり, これは式5の発散を取ることと一致します. 同様に, 両方のタイプの誘導電流密度を含み, 完全なマックスウェル定式化である周波数領域の研究では, \nabla \cdot \textbf{A} = 0という制約の代わりに, スタディで制御されたゲージ固定により, 全電流密度\nabla \cdot \textbf{J} = 0対して\textbf{J}が強制されています. このような発散制約を用いることの主な利点は, 特に静的限界に近づく際の数値安定性の向上です.
ご自分で: ゲージ固定を試す
ゲージ固定の理解を深めるには, ご自分で実験をしていただくのが一番です. 下の表は, アプリケーションライブラリにあるいくつかのモデルを, ゲージ固定なしとゲージ固定ありで解き, その結果と計算時間を比較したものです. 例えば, Eコアトランスのモデルでは, 直接ソルバーでゲージ固定を行い, 電気伝導度をゼロに設定して解いています. また, ゲージ固定をせずに, 同じ直接ソルバーで, すべての領域で\sigma=1S/mとし, コイル領域の安定化電気伝導度にも設定することで解くこともできます. このモデルは, ゲージ固定を使用した場合に比べて, 約半分の計算時間で解けることがわかります.
| フィジックスインターフェース | スタディタイプ | アプリケーションギャラリで見たモデル |
|---|---|---|
| mf | 固定 | ヘルムホルツコイル |
| 時間依存 | Eコアトランス | |
| 周波数領域 | 渦電流 | |
| mef | 周波数領域 | パワーインダクター |
| rmm | 時間依存 | 永久磁石モーター |
まとめ
このブログでは, まず, AC/DCモジュールを使った電磁気学シミュレーションでは, 直接ソルバーを使用する必要がない限り, ゲージ固定は必要ないことをご説明しました. 次に, 関連する3つのフィジックスインターフェースでゲージ固定がどのように実装使用されているかを示し, ゲージ固定の利点と欠点について議論しました. 最後に, 皆さんに試していただきたい興味深いモデルをリストとして挙げました.



コメント (0)